“零分解”在解题中的应用
——对2010年海南高考一道试题的解答与探讨
郭秀丽,郭晋生
(吕梁市贺昌中学校,山西 吕梁 033000)
一、“零分解”的概念
“零分解”就是无中生有,将“0”分解为两个相反的量,加在方程里。因为任何两个相反量的和是零,在方程中加一个“0”,即加两个相反的量,方程的解是不变的。我们都熟悉的在数学上解方程“移项变号”法则其本质就是“零分解”,在方程的两边加上相同的量就是在方程中加上了两个相反的量,其结果就成了“移项变号”的解题法则。在应用过程中根据解题需要针对性地选择“无中生有”,“零分解”,使添加的两个相反量与原方程中的已有量形成巧妙的组合,会使解题更方便简洁。“零分解”的方法可以替代使用“非惯性参考系”引进“惯性力”这个超过高中物理教学大纲的传统方法,而且也开辟了一个全新的思路,拓展了思维。“零分解”方法的具体使用如下:

如右图,斜面体M向左做加速运动,讨论斜面上的物体m的动力学、运动学问题时,传统的方法是以斜面体M为参考系,给物体m添加一个向右的惯性力ma,从而解析物体m相对斜面体M的动力学、运动学问题。“零分解”的方法是仍然以地面为参考系,把物体m的运动分解为与斜面体M相同的一个分运动和相对斜面体M的另一个分运动。应用“零分解”,给物体m添加一对相反的力——向左的ma和向右的ma,向左的力ma就是物体与斜面体一起向左加速运动需要的力,向右的力ma与物体受到的真实的力的合力就是物体m相对斜面体M沿斜面运动的力。
引进非惯性系,添加惯性力的方法不但超过教学大纲、高考大纲,而且学生也难以理解,基本靠记忆式学习。而“零分解”的方法,根据教材上力的分解与运动的分解这个教学的基本内容拓展、应用,学生容易理解,能自觉使用,与教学教材、高考大纲一脉相通,改记忆式学习为理解基础上的学习活动。
二、对一道高考题应用“零分解”进行分析、解答
(2010年海南高考题)水平地面上有一楔形物块A,其斜面上有一小物块B,B与平行于斜面的细绳的一端相连,细绳另一端固定在斜面上,A与B之间光滑,A和B以共同速度在地面的光滑段向左运动。当它们刚运动到粗糙段时:(高考给出的标准答案是C选项)

图1图2
A.绳的张力减小,B对A的正压力减小
B.绳的张力增加,斜面对B的正压力增加
C.绳的张力减小,地面对A的支持力增加
D.绳的张力增加,地面对A的支持力减小



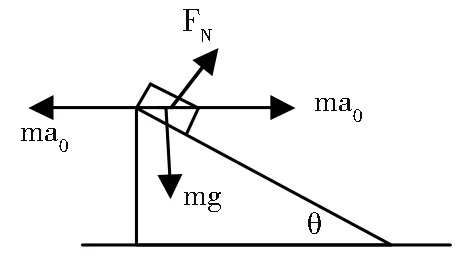
如果选择A、B及细绳整体为研究对象,在竖直方向有:N′=Mg+mg=N,水平方向有f=μN′(本题不求摩擦力)。
结论1:当斜面受到的摩擦力比较小时,斜面A做减速运动的加速度比较小,地面对A的支持力没有变化。细绳对物体B的拉力变小。
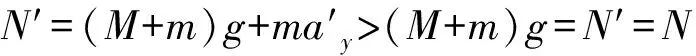
当a≤gtanθ时,A、B一起减速运动,μ(M+m)g=(M+m)a,得μ≤tanθ,这时地面对A的支持力没有变化;当a>gtanθ,即μ>tanθ时,B相对A沿斜面向上运动,这时地面对A的支持力增大。
结论2:当斜面的加速度a>gtnaθ(即μ>tanθ)时,地面对斜面体的支持力增大了,细绳对物体B的拉力变小。
结论:当μ≤tanθ时,地面对A的支持力没有变化;当μ>tanθ时,地面对A的支持力变大。细绳对物体B的拉力减小或没有拉力。
通过上面的分析得出两种情况,其实再细致分析一下过程还是比较复杂的。我们知道地面对A的摩擦力是逐渐增大的,因为f=μN*,N*是压在粗糙面上的压力,N*是从零开始逐渐增大的。这道题给的时空状态是“刚运动到粗糙段时”,f从0开始逐渐增大,a亦从0开始逐渐增大,所以选择地面对A的支持力没有变化更妥当,因为系统刚运动到粗糙平面时,摩擦力f很小, 加速度a也很小 , 这个从斜面A不断进入粗糙地面的过程是连续变化的,题设的“刚运动到粗糙段时”是过程的左极限时态。
高考的答案,是C选项。但是通过上面的分析、解答,答案应该是“细绳的拉力减小,地面对A的支持力不变”更符合题意。
方法二:本题还可以从做功和能量变化来分析,系统进入粗糙面后,若μ≤tanθ,A、B一起减速运动,重力对B不做功,支持力对B做负功,细绳的拉力对B做正功,支持力增大,拉力减小,支持力与拉力做的总功是负功(因为在光滑平面匀速运动时支持力与拉力的合力与重力平衡,支持力与拉力的总功是零),物体B可以与斜面体A一起做减速运动。若μ>tanθ,B相对A沿斜面向上运动冲上斜面,这时拉力为零,做负功的支持力增大,B的动能减小,势能增大,总能量减小。若斜面体A突然停止运动,物体B一定冲上斜面,动能减小,势能增大,总能量不变,因为没有耗散力做功。从功和能的角度分析也符合前面用牛顿运动定律分析的结果。用功和能来分析物理过程一般相对比较简单,因为功和能是标量,但是正因为功是过程量,能量是状态量,分析的比较粗略;用牛顿运动定律分析物理过程比较细腻,往往要结合运动学的规律,一般关系方程比较多,稍显复杂。两种分析方法都要很好的掌握,互相验证,相得益彰。
若应用爱因斯坦的广义相对论“加速场等价于引力场”来分析这个问题,A的加速度是向右的,等价的引力场是向左的,若B相对A没有沿斜面向上加速运动,A、B系统在竖直方向的外力没有变化,即地面对斜面A的支持力没有变化。若B相对A沿斜面向上加速运动,则A、B系统竖直方向的合外力向下,地面对A的支持力FN<(mA+mB)g。
上面我们是把A、B基本视为质点来分析的,若将B视为质点(或非质点),A视为刚体(非质点),且μ足够大,θ(斜面的倾角)足够大,A、B系统的惯性力的力矩会大于系统重力的力矩(根据爱因斯坦的广义相对论惯性力与重力(引力)是等价的,均为主动力)。系统会倾倒,倾倒的临界状态摩擦力与支持力的力矩均为零。如图3。
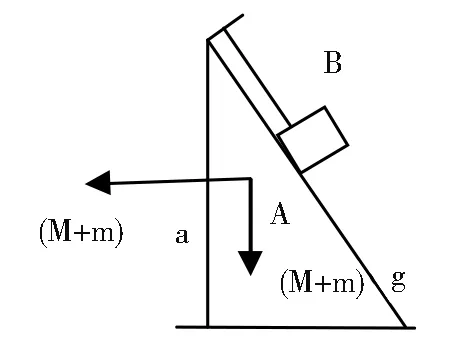
图3

从上面的分析、解答,可以看出高考题给出的标准答案是不正确的。笔者认为答案应该是:细绳的拉力减小或消失,A、B间相互作用的弹力增大,地面对A的支持力在μ≤tanθ没有变化,在μ>tanθ增大。
若突出、强调“刚运动到粗糙平面时”这个时态,或把物体视为非质点,对问题的讨论会更微妙和复杂一些,如上所述。
三、几个应用“零分解”解题的案例
例1 在光滑的水平面上有一质量为M,倾角为θ的斜面,在斜面上的有一质量为m的物块受到一外力F的作用,F平行于斜面向上。物块与斜面间的动摩擦因数为μ,若要使物块在斜面上沿斜面向上相对滑动,求F满足的条件。(最大静摩擦力等于滑动摩擦力)

提示:我们可以求临界值F0,即此时系统(M和m)的加速度相同,令为a0,方向向左,M、m相互作用的摩擦力是最大静摩擦力f0=μFN,a0=Fcosθ/(M+m)。用“零分解”的方法,给物块m添加一对向左、向右的力ma0,除去向左的力ma0,(向左的力ma0看作是物块m产生与斜面相同加速度的力),其余的力(重力mg、拉力F0、支持力FN、摩擦力f0、还有向右的力ma0)满足相对斜面静止的平衡方程。
有:对系统
F0cosθ=(M+m)a0
(1)
对物块,在垂直于斜面方向
FN=mgcosθ-ma0sinθ
(2)
在平行于斜面方向
F0=mgsinθ+ma0cosθ+μFN
(3)
得
(4)
当m相对M发生向上相对运动时,
例2 如图,一物块静止放置在倾角为θ的斜面上,质量为m,物块与斜面之间的动摩擦因数为μ,斜面在水平地面上以加速度a向右匀加速运动。求a满足什么条件时物块将开始滑动?

提示:可以用“零分解”来解答。给物块m添加一对力,向左的力ma和向右的力ma,向右的力ma是物块随斜面一起做加速运动需要的力,向左的力ma、重力mg、支持力FN、沿斜面向上的摩擦力f,这些力满足物块相对斜面静止(或匀速下滑)的动力学条件,其中f=μFN。
在平行于斜面方向
f=mgsinθ+ma0cosθ
(5)
在垂直于斜面方向
FN=mgcosθ-ma0sinθ
(6)
又
f=μFN
(7)


例3 一个表面光滑的截面为直角三角形的楔形物体,斜面的长度为L,斜面与底边之间的夹角为θ,质量为M,静止于光滑的水平桌面上,将一个质量为m的质点放在斜面的顶端,该质点从斜面自由滑下,

解:令楔形物体M向左运动的加速度为a0,给视为质点的物块m一对力,向左的ma0和向右的ma0,向左的ma0是物块m与楔形物体一起向左加速运动需要的力,重力mg、支持力FN、水平向右的力ma0,这三个力的合力是使物块m相对楔形物体M沿斜面加速下滑的力。于是可以列出方程:
对物块相对位移
(8)
a是物块相对楔形物体的加速度
楔形物体的位移
(9)
平行于斜面方向
ma0cosθ+mgsinθ=ma
(10)
系统在水平方向动量守恒
matcosθ=(M+m)a0t
(11)
由(11)式得
(12)
由(8)(9)(12)式得
(13)
由(10)(12)式得
(14)
将(14)式代入(8)式得
(15)
例4 三个物体通过滑轮组及细绳互相连接,它们的质量m1=4 m,m2=2 m,m3= m,不计滑轮质量和一切摩擦,求m1物块的加速度和两条绳上的张力。
(a1=2m/s2T1=2T2=3.2mg)

解:因为m1>m2+m3,所以m1向下加速运动,令m1向下的加速度大小为a1,以地面为参考系,用“零分解”的方法,给m2添加一对向上、向下的力m2a1,给m3添加一对向上、向下的力m3a1,向上的力m2a1、m3a1是m2和m3随动滑轮向上加速运动需要的力,于是有:
m1g-T1=m1a1
(16)
m2g+m2a1-T2=m2a2
(17)
T2-m3g-m3a1=m3a3
(18)
T1=2T2
(19)
a2=a3
(20)
其中a1是m1相对地面的加速度,a2、a3分别是m2、m3相对动滑轮的加速度。
由上面五个方程很容易求得解答。
用“零分解”解题,既很方便也很好理解。“零分解”的本质就是添加一对相反量(其和是0),不影响原题的数量关系。“零分解”还可以用在其他问题上。
例5 一个半径为R的圆周上对称地分布着8个等量的点电荷,电荷量为q,其中一个为负电荷,其余为正电荷,求圆心处的电场强度。(E=4Kq/R2)

提示:在负电荷处添加一个正电荷和一个负电荷,此正电荷与其余7个正电荷由于对称分布,这8个电荷在圆心的场强为零,于是圆心处的场强就是-2q点电荷在该处产生的场强。
一种方法不仅仅是一个技巧,其命名潜示着认知角度、思想方法、物理理念。譬如引入“惯性力”,就是从参考系入手,为了使牛顿运动定律在非惯性系中也能适用而“凭空”添加的一个力。现在看来正是爱因斯坦广义相对论的等价性原理,“加速场等价于引力场,加速场与引力场是不能区分的”。“零分解”暗合着宇宙大爆炸理论,我们的宇宙就是从一个奇点大爆炸而产生的,生成了正反两种物质,如果我们的宇宙没有外宇宙的作用,宇宙的总能量、总动量是守恒的,宇宙是一个自洽系统。“零分解”里面隐含物理的味道,自然的气息。也许这样太浪漫了,宇宙就是浪漫的。
教学改革的核心就是激发学生的学习兴趣,开发学生的学习潜能。希望教师、学生能解放思想,开拓创新,深化教学改革。

