基于有效翼缘内板筋影响的RC框架结构破坏机制分析
罗水华,黄文颖,吴应雄
(1.福建江夏学院 工程学院, 福建 福州 350108;2.福州大学 土木工程学院, 福建 福州 350108)
通过对现浇RC框架结构的震害调查,结果表明,多数严格按照建筑抗震规范设计的建筑,仍然难以实现“强柱弱梁”的预期破坏机制[1-6]。现浇楼板的存在对“强柱弱梁”的实现有较大的影响[7-9]。针对这一因素,目前中国抗震规范[10]的做法是,通过放大梁刚度以考虑现浇楼板对其刚度的影响,通过调整系数法提高柱抗剪强度以期实现“强柱弱梁”的目标,而并未充分考虑现浇楼板与梁协同作用下,与梁平行的板内钢筋对梁端抗弯承载能力的提高作用。研究表明[11-13],板内钢筋参与抗弯作用使得节点处负弯矩区梁屈服弯矩实测值比无翼缘梁高出了30%左右,“强柱弱梁”破坏机制难以实现。
在框架梁负弯矩区,与梁平行的板内钢筋对梁端抗弯承载能力的提高作用与其所在位置相关,距离梁位置越远板筋参与程度越小[14],假定在某等效宽度内板筋全部参与梁端抗弯作用,这一等效宽度即定义为梁有效翼缘宽度。为考虑有效翼缘内板筋影响,新西兰建筑规范规定,在梁端负弯矩区,矩形截面内梁的实配钢筋面积是扣减了相应板筋加强作用后的面积。大量学者对有效翼缘宽度取值进行了研究[15-18]且给出了建议性取值方法。其中,王素裹[19]通过对RC框架模型的板筋受力分布规律进行了大量的数值模拟,对翼缘宽度分布规律进行数值回归,得出在综合考虑了节点位置、轴压比和正交梁跨度等因素下的有效翼缘计算公式;陈紫平[20]利用MTS电液压伺服系统对一个单层单跨三维空间RC框架结构进行往复加载,测得板筋的受力分布规律与文献[19]结论一致;黄福智[21]结合文献[19]中有效翼缘宽度的取值方法,对一个5层RC框架结构缩尺模型进行振动台试验,得出考虑梁有效翼缘宽度内板筋增强作用并减少矩形梁端配筋的模型,在地震作用下节点处柱抗震能力强于梁。
目前RC框架“强柱弱梁”破坏机制已较清晰,但较少运用梁有效翼缘公式计入现浇楼板中板筋的影响,并对节点进行配筋优化,探究配筋优化后模型地震作用下的破坏机制。本文结合学者对梁有效翼缘公式取值方法计算板筋面积,通过降低矩形梁配筋的方法对节点进行配筋优化,运用OpenSEES有限元软件对模型进行数值分析,研究模型的安全性和破坏机制,为结构分析计算提出几点建议。
1 梁有效翼缘宽度取值
图1所示为有效翼缘bf的定义,框架梁在负弯矩区bf范围内的板筋全部参与作用。
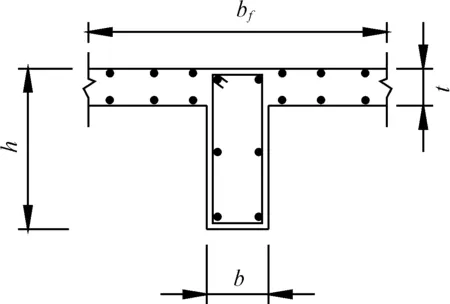
图1 “有效翼缘宽度”定义简图
王素裹根据不同位置处板筋的应力分布情况,提出了公式(1)—公式(4)的梁有效翼缘宽度简化计算方法,公式中的边榀和中间榀与水平向主荷载方向相对应,这些公式同时考虑了节点位置、柱轴压比和正交梁跨度。另外,这些公式主要适用于层间位移角达到1/50的情况下,因在结构破坏时层间位移角一般较大,这与实际情况相符合。
边榀边节点:
bf=(-1.701n3+3.062n2-1.906n+0.757)ln
(1)
边榀中节点:
bf=(-0.479n3+0.015n2+0.14n+0.356)ln
(2)
中间榀边节点:
bf=(-3.421n3+5.820n2-3.566n+1.443)ln
(3)
中间榀中节点:
bf=(2.940n3-6.442n2+3.502n+0.108)ln
(4)
式中:bf为梁有效翼缘宽度;n为结构轴压比;ln为正交梁净跨。
在地震作用下,当结构层间位移角较大时,在计入有效翼缘内板筋参与作用后,为实现节点处梁先于柱破坏,节点处抗弯承载力应满足式(5),其中,有效翼缘宽度按式(1)—式(4)计算:
∑Mcua>∑Mbua+Ms
(5)
式中: ∑Mcua为柱端实际抗弯承载力;∑Mbua为矩形梁截面内实际抗弯承载能力;Ms为板筋所受弯矩。bf范围内板筋面积Asf为:
Asf=(ρss+ρsb)tbf
(6)
式中:ρss和ρsb是板面与板底配筋率,t为板厚。
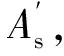
(7)
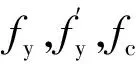
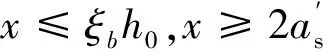
(8)
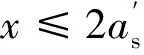
(9)
结构节点配筋优化过程为:首先通过PKPM有限元软件计算模型初始配筋;其次通过公式(1)—公式(4)和公式(6)计算bf值和Asf值;最后通过公式(7)—公式(9)计算节点负弯矩处梁实际抗弯承载力,并根据公式(5)调整矩形梁和柱配筋值,保证柱端实际抗弯承载能力大于梁端,最终达到梁先于柱产生塑性铰的目标。
2 模型的破坏机制分析
2.1 模型介绍及模拟方法
结构设计基本信息为:抗震等级为三级的现浇RC框架结构,中间为走道,x向总长12.6 m,y向总长10.2 m,其基本尺寸见平面图2,结构总层数为5层,层高为3.0 m。抗震设防烈度为7度(0.1g),场地类别为Ⅱ类,设计地震分组为第二组;结构荷载取值见表1。

表1 结构荷载取值
注:恒载均不包含结构自重,梁上墙载取7.0 kN/m。
混凝土强度等级为C30,受力钢筋为HRB335,箍筋为HRB300,钢筋弹性模量取2.0×105MPa。结构构件基本尺寸为:柱截面为400 mm×400 mm;梁截面为400 mm×200 mm;板厚120 mm。利用第2节中介绍的方法,对结构配筋进行调整,运用公式(1)—公式(4)计算所得有效翼缘宽度列于表2中。
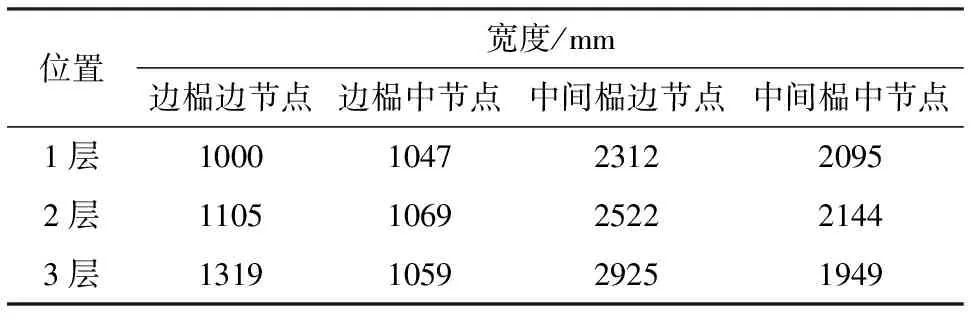
表2 有效翼缘宽度取值
通过公式(7)—公式(9)计算节点处梁端实际承载力,对梁柱配筋进行调整后配筋情况如下:柱区分中柱和边(角)柱,底层中柱配筋面积为39 cm2,底层边(角)柱配筋面积为25 cm2。y方向梁支座负筋配筋面积为4 cm2,其余部位梁配筋面积采用PKPM有限元软件计算得出。LB1沿y方向板筋配筋率为0.53%(该数值为板底和板面配筋之和,余同),LB2沿y方向板筋配筋率为0.47。梁柱节点均能满足公式(5)的要求。
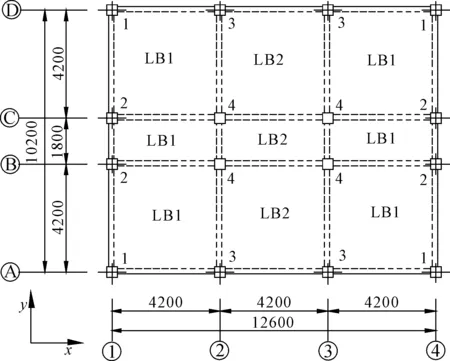
注:“1”为边榀边节点;“2”为边榀中节点;
运用OpenSEES有限元分析软件建立数值模型[22]。使用Tool Command Language,将公式(1)—公式(4)编写成BuildRCrectSection命令流,实现建模中快速套用公式。在运用OpenSEES建模时,混凝土、钢筋和截面恢复力模型分别采用Concrete 02、Steel 02和Fiber Section模型。将控制截面中的混凝土离散成40个纤维。梁柱采用杆系模型,每个杆件等分为四个dispBeamColumn单元。在求解过程中,将每个dispBeamColumn的积分数设置为5。
针对Ⅱ类场地和其特征周期,从PEER地震数据库中选择2条天然地震动和1条常用于中国福建省结构抗震设计的人工地震动(Rgbtongan),输入方向为y方向。三条波均满足现行规范[10]第5.1.2条的规定。根据抗震规范对7度0.1g区的相关规定,设置了表3的加载工况,为观察结构在超烈度作用下的屈服模式,对结构再输入加速度峰值(简称为PGA)为0.35g和0.5g的地震波,模型加载工况见表3。
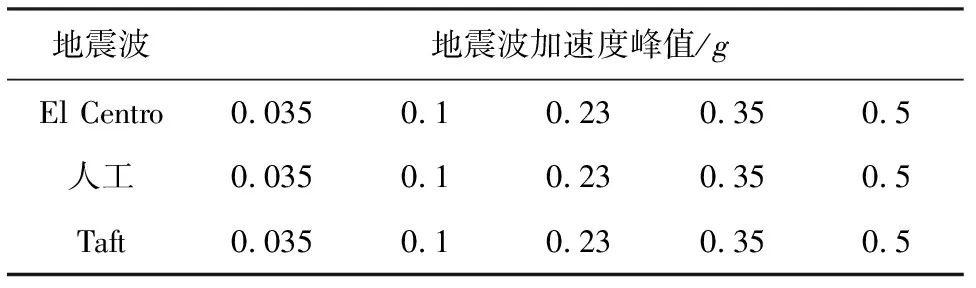
表3 加载工况
2.2 结构位移响应和塑性铰分析
2.2.1 结构位移响应
模型阻尼比ξ=0.05。经计算可得,瑞雷阻尼系数a0=0.3828,a1=0.0065,自振频率为ω1=7.38,ω2=7.96,结构的第一周期T1=0.85 s,第二周期T2=0.79 s。
不同荷载工况下最大层间位移和位移角如表4所示。取PGA相等时,三种地震波作用下结构最大层间位移均值和最大层间位移角均值,绘制出结构位移响应图,如图3所示。根据我国抗震规范相关规定,当层间位移角达到1/50时,结构已严重破坏。
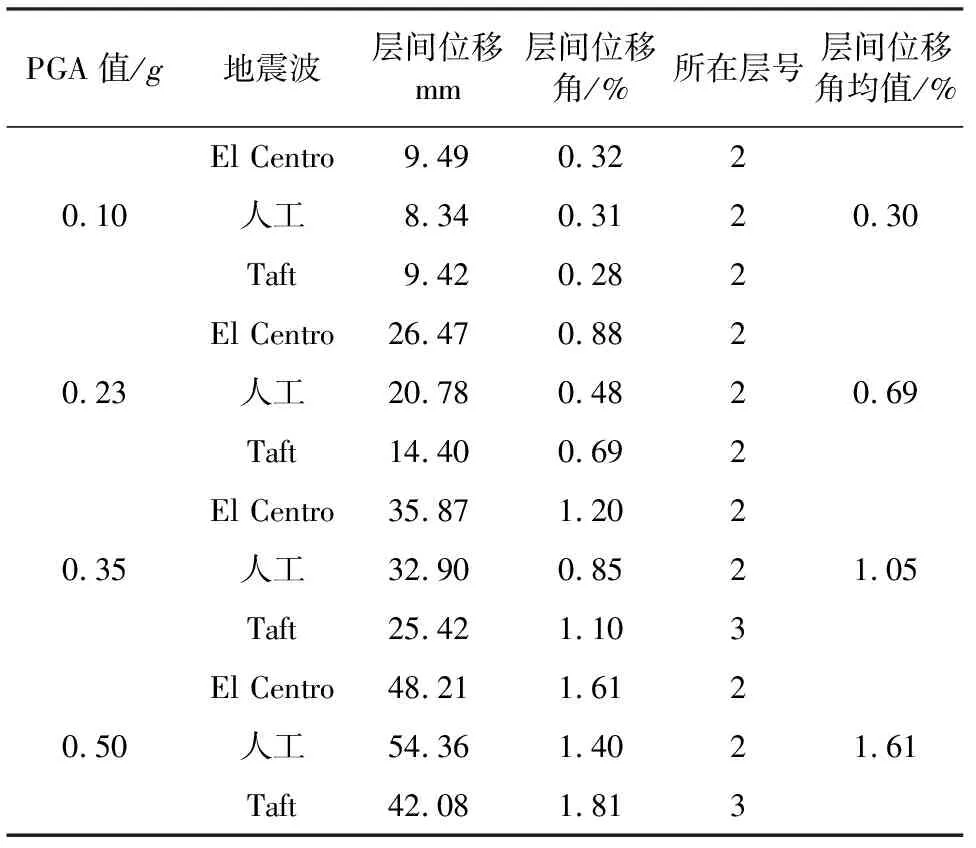
表4 最大层间位移和位移角
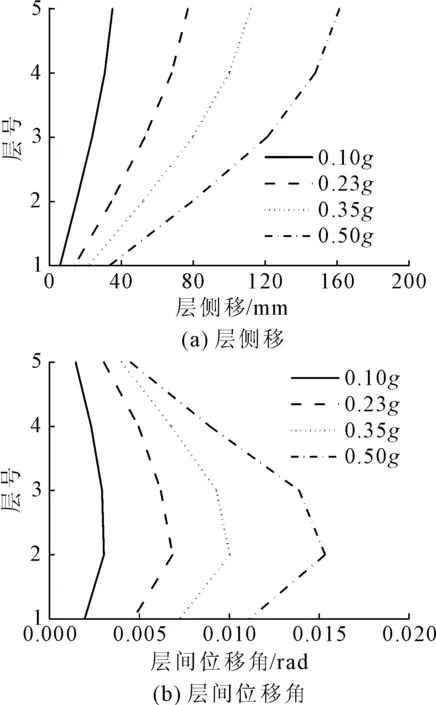
图3 结构位移响应曲线图
由表4和图3可得:当PGA=0.1g和0.23g时,最大层间位移角分别为0.30%和0.69%,均小于规范中的限值2%,结构在设防烈度作用下和罕遇地震作用下能满足“大震不倒”的安全性要求。随着PGA的增大,结构层间位移增大,当PGA等于0.50g时,层间位移角为1.61%,顶层位移为161.3 mm,接近规范限值,结构处于严重破坏状态。如图3所示在不同PGA地震作用下,二层位置位移响应最明显,首层和三层的位移响应次之,其他楼层处层间位移较小,结构的破坏主要集中在一到三层。
在设防烈度和罕遇地震作用下,通过对结构的位移响应分析可得:由公式(1)—公式(4)计算 范围内板筋参与抗弯作用,并对节点配筋进行调整后的结构,虽然降低了矩形梁端负弯矩区的配筋,但结构能够满足抗震设计规范中的安全性要求。
2.2.2 梁和柱出铰情况
地震作用下,结构构件将产生复杂的应力应变,构件转角能够综合反映构件的受力情况和截面变形,且简单直观,因此本文以转角大小来判断构件所处状态。根据美国FEM356规范相关规定,一般情况下,当构件转角达到0.002 rad时,构件可判定为屈服。将转角分为“单向较”和“双向铰”,“单向铰”表示结构梁(柱)端仅一个方向出铰,“双向铰”表示结构梁(柱)端两个方向均出铰。为便于后续对梁柱塑性铰转角大小对比,在图4中对破坏最为严重的节点进行编号。在Taft波和人工波作用下,结构出铰规律与在El Centro波作用下一致,本文将主要分析El Centro波作用下梁柱出铰规律。
图4是PGA等于0.23g时,梁柱塑性铰分布图。根据梁(柱)端转角大小(简称为“θ”)将其分为图4中的四类,以方便描述构件破坏程度。表5是PGA等于0.23g时,节点破坏最为严重处的构件转角值。
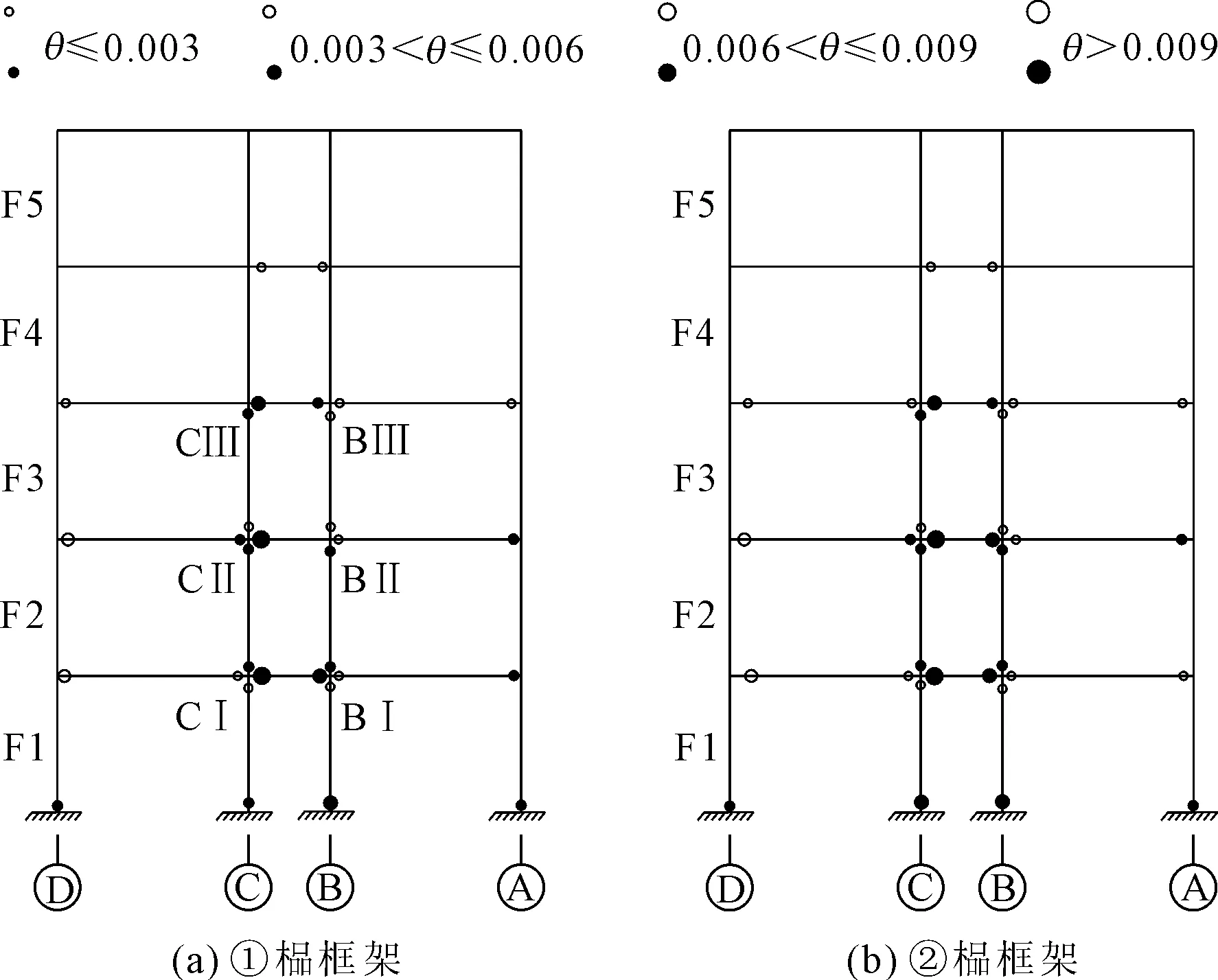
注:实心铰表示双向出铰,空心铰表示单向出铰,余同
图4 PGA=0.23g时梁柱塑性铰分布图
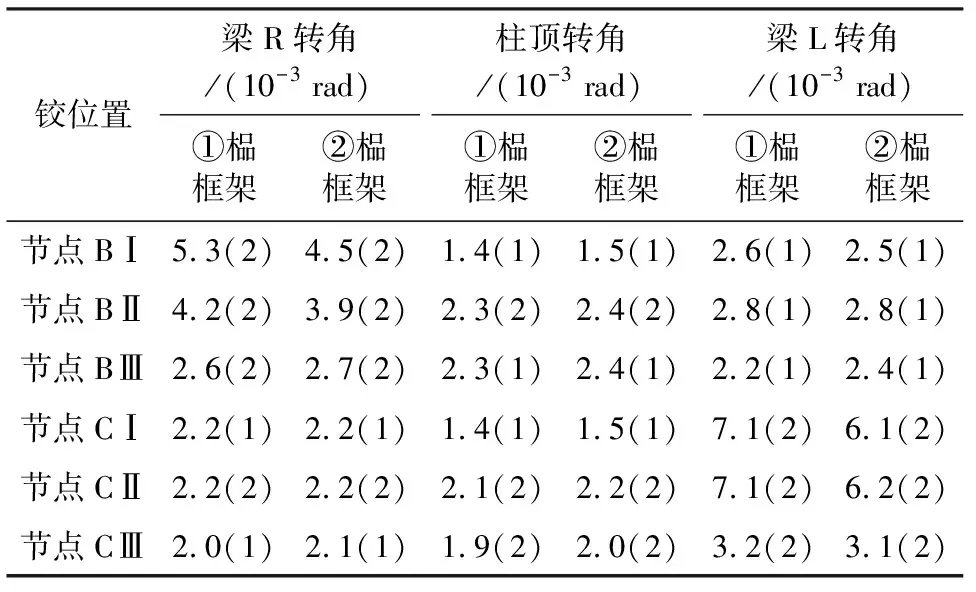
表5 PGA=0.23g时梁(柱)端塑性铰转角大小
注:括号内数值“1”代表单向出铰,“2”代表双向出铰,余同。“梁R”表示位于节点右侧的梁端,“梁L”表示位于节点左侧的梁端。
分析图4和表5,在罕遇地震作用下结构梁柱端塑性铰出铰情况如下:
(1) 柱端塑性铰情况:总体上看,θ值均小于0.003,出铰位置主要在B、C轴处一层柱顶、二层三层柱底和柱顶,底层柱底全部出双向铰,其余位置未出铰。由于中柱相对于边柱、②榀框架处的柱子相对于①榀框架处的柱子,轴压比更大,导致中柱损伤程度严重于边柱,②榀框架柱θ值大于①榀框架柱。
(2) 梁端塑性铰情况:梁出铰数和塑性铰转角大小总体大于柱;由于中间跨为短跨,梁端承受较大负弯矩作用,中间小跨处梁端破坏较严重;一二层梁端均出铰,且θ值大小较接近;三层处大部分梁端均出现塑性铰,且θ值以0.003以内者居多;四层出现少数塑性铰,五层梁端不出现塑性铰。
(3) 由表5可得,梁端转角大于柱端。除底层柱底外,二层处柱顶θ值最大,二层柱顶位置为较薄弱位置,这与二层层间位移最大相对应;同一节点中BⅠ—BⅢ右位置梁端θ值大于左位置梁端θ值,表现在CⅠ—CⅢ位置时规律一致,走廊处梁端θ值最大。结构的这些行为主要与地震作用下各节点受力状态相关。
模型在罕遇地震作用下结构各处有不同程度的破坏,总体表现出梁端出铰数目较多、塑性铰转角较大,结构表现为“强柱弱梁”的屈服模式。
同理,当PGA增大到0.35g时,梁端塑性铰多数由单向转为双向、出铰位置增多并向上延伸,原有塑性铰转角大小增大。柱端塑性铰数目略有增加,原有的塑性铰θ值增大。随着PGA的增大,梁端塑性铰θ值增长速度明显比柱端快,以破坏最严重的②榀框架CⅡ处为例,柱θ值增加0.008,同位置处“梁R”和“梁L”θ值分别增大0.001 9和0.001 4。从数目上看,同一根梁左右两端均出铰(顶层除外),柱端出铰位置明显少于梁端,边节点和顶层处,只见梁端出铰。结构主要通过梁的塑性铰的增多增大耗能。
当PGA增大到0.50g时,梁端塑性铰θ值多数大于0.006,且在2~3层走廊处梁端出现了θ值大于0.009的情况;柱端塑性铰增多增大,但θ值均在0.006以内(底层柱脚除外),边柱柱顶开始出现塑性铰。结合结构的位移响应,结构破坏程度严重。结构表现出的屈服机制为“强柱弱梁”。需值得关注的是结构底层柱底θ值大多分布在0.006和0.009之间,应对底层柱底强度予以加强,防止地震作用下底层柱底破坏而导致结构整体失稳。
综上分析,运用有效翼缘宽度简化公式(1)—公式(4)减少了矩形梁端配筋的模型,在同一PGA作用下结构梁端塑性铰与同节点处柱端相比数目多转角大,PGA增大时梁端铰增长速度比柱快,实现了“强柱弱梁”破坏机制,可以考虑在结构配筋计算时结合公式(1)—公式(4)计算有效翼缘宽度,减少矩形梁端配筋;虽然梁柱节点处实现了梁先于柱破坏,但底层柱脚处为结构薄弱点需值得关注,应防止地震作用下底层柱底破坏而导致结构整体失稳。
3 结 论
(1) 考虑板筋对梁端抗弯承载力增强后的模型能够满足抗震设计规范中的安全性要求。模型虽然降低了梁端负弯矩区的配筋,但该部分弯矩实际由有效翼缘内板筋承担,通过对结构的位移反应、层间位移角分布分析,表明结构能够满足抗震设计规范中对现浇RC框架的安全性要求。
(2) 考虑板筋作用后的模型能够实现“强柱弱梁”目标破坏机制。通过分析节点处梁柱塑性铰分布情况和增长情况表明,柱端损伤情况小于梁端,结构的耗能方式主要以梁端的塑性铰增多增大为主。
(3) 可结合有效翼缘简化公式计算参与抗弯作用的板筋面积。有效翼缘简化公式综合考虑了轴压比、节点位置和正交梁跨度等相关因素,可以考虑在结构配筋计算时,计入有效翼缘宽度板筋参与作用并优化节点配筋。
(4) 虽然模型实现了“强柱弱梁”破坏机制,但底层柱脚处为结构薄弱点需值得关注,应对底层柱底强度予以加强,防止地震作用下底层柱底破坏而导致结构整体失稳。

