管道悬空灾害的分布式光纤实时监测方法研究
赵 毅,滕建强,2,杨耀辉,冯 新
(1.中国石油化工股份有限公司 西北油田分公司, 新疆 乌鲁木齐 830011;2.中国石化缝洞型油藏提高采收率重点实验室, 新疆 乌鲁木齐 830011;3.大连理工大学 建设工程学部, 辽宁 大连 116024)
根据国家发改委发布的《中长期油气管网规划》,预计到2020年,全国油气管网规模将达到16.9万km,其中原油、成品油、天然气管道里程分别为3.2万km、3.3万km、10.4万km;到2025年,全国油气管网规模将进一步扩大到24万km。因此,我国油气管网还将处于一个较长的发展时期。我国幅员辽阔,油气藏的分布极不均匀,油气管道面临复杂的地质和自然灾害情况。国际上的经验表明,虽然第三方破坏、腐蚀、误操作等因素是导致管网失效的主要原因,但是对于存在地质灾害风险的区域,因滑坡、侵蚀、沉降、流动沙丘以及洪水等地质或自然灾害造成的管道断裂却频繁发生,且后果远较一般地区更为严重[1]。例如,发生于1987年的厄瓜多尔管线断裂事件,因强降雨及地震引发滑坡,导致Trans-Ecuadorian管线系统的70 km管道遭受破坏,造成了历史上单一管线的最大事故,仅修复就花费了6个月的时间,直接、间接经济损失巨大[2]。
滑坡、侵蚀、流动沙丘等地质灾害通常导致管道发生悬空,引起管壁出现较大的弯曲应力,严重时造成管道断裂事故。但是对于沙漠或山区等野外条件,管道悬空的及时发现却极其困难。尽管激光雷达(LiDAR)和无人机(UAV)等新技术已经在管道完整性检测中得到应用[3-4],但是这些技术存在无法实时监测、成本高、数据解释困难的问题,还不能满足长输油气管道悬空监测和预警的要求。近年来,分布式光纤传感技术逐渐应用于埋地和海底管道,它具有实时监测、远程传感、分布式测量的优势,可以在线获得管道任意位置应变和泄漏等在位状态[5-9]。管道悬空将引起复杂的管-土相互作用,如何根据管道的应变分布评价管道悬空状态,目前仍是一个挑战性的问题。笔者基于悬空管道的力学响应机理,提出一种监测管道悬空灾害的分布式光纤监测方法,并通过一系列的模型试验研究方法的有效性。
1 监测方法
1.1 埋地管道悬空监测原理
埋地管道在自重、覆土荷载、交通荷载等作用下,与地基土体之间将发生复杂的相互作用。为了描述管-土相互作用,通常将埋地管道视为受到弹簧约束作用的无限地基梁,其中最为常用的是Winkler模型[10]。在Winkler模型中,地基土体的约束作用由一系列等间距排列、相互独立的弹簧所代替,每一个弹簧向管道提供法向或切向的抵抗作用,其作用可用单参数、双参数或三参数来描述。若只考虑竖直面内的管-土相互作用,则系统的控制方程可写为:
(1)
而管道一旦因引言所述的各种原因形成悬空(如图1(a)所示),则难以利用Winkler模型获得管道力学响应的分析解答, 但是我们仍然可以根据管-土相互作用的基本原理,考察悬空管道的力学行为。假设管道非悬空部分仍为弹性地基上的无限长梁,在悬空段由于土体支撑作用的丧失,管道在自重作用下发生向下的挠曲变形,挠度在悬空段中点达到最大。随着位置向两侧土体趋近,管道挠曲变形逐渐减小。当管道由悬空段进入两侧土体后,土体仍然向管道提供约束作用,挠曲变形进一步减小,但是由于变形协调,其变形的方向将发生变化,并且随着位置逐渐远离悬空段,反方向的挠曲变形先增加后减小,直至消失,在变形消失处形成了两个“锚固点”,我们将悬空段两侧坡肩至锚固点的范围定义为“转换段”。在转换段内,土体仍可被视作Winkler模型的土弹簧,若将该段土体约束作用离散为等间距的土弹簧,则管道悬空段和转换段的力学模型如图1(b)所示,于是这三段管道便成为一个具有弹性支撑的连续梁,其边界条件(锚固点)为简支。根据结构力学原理可知,悬空导致的附加弯矩分布如图1(c)。其中,锚固点以外的管道不会因悬空而产生附加弯矩;悬空段会在跨中形成最大正弯矩,然后向两侧逐渐减小,并且在靠近转换段处形成负弯矩区;在转换段的起点即坡肩处,负弯矩达到最大值,形成反弯点,然后负弯矩逐渐减小,至锚固点处则完全消失。图1(c)所示的附加弯矩分布给出了悬空导致的管道应变/应力变化曲线,如果通过监测获得两个相继状态的管道应变分布曲线具有图1(c)的形状,就可以判断管道出现了悬空,并且可以判断管道悬空段和转换段的位置和长度。
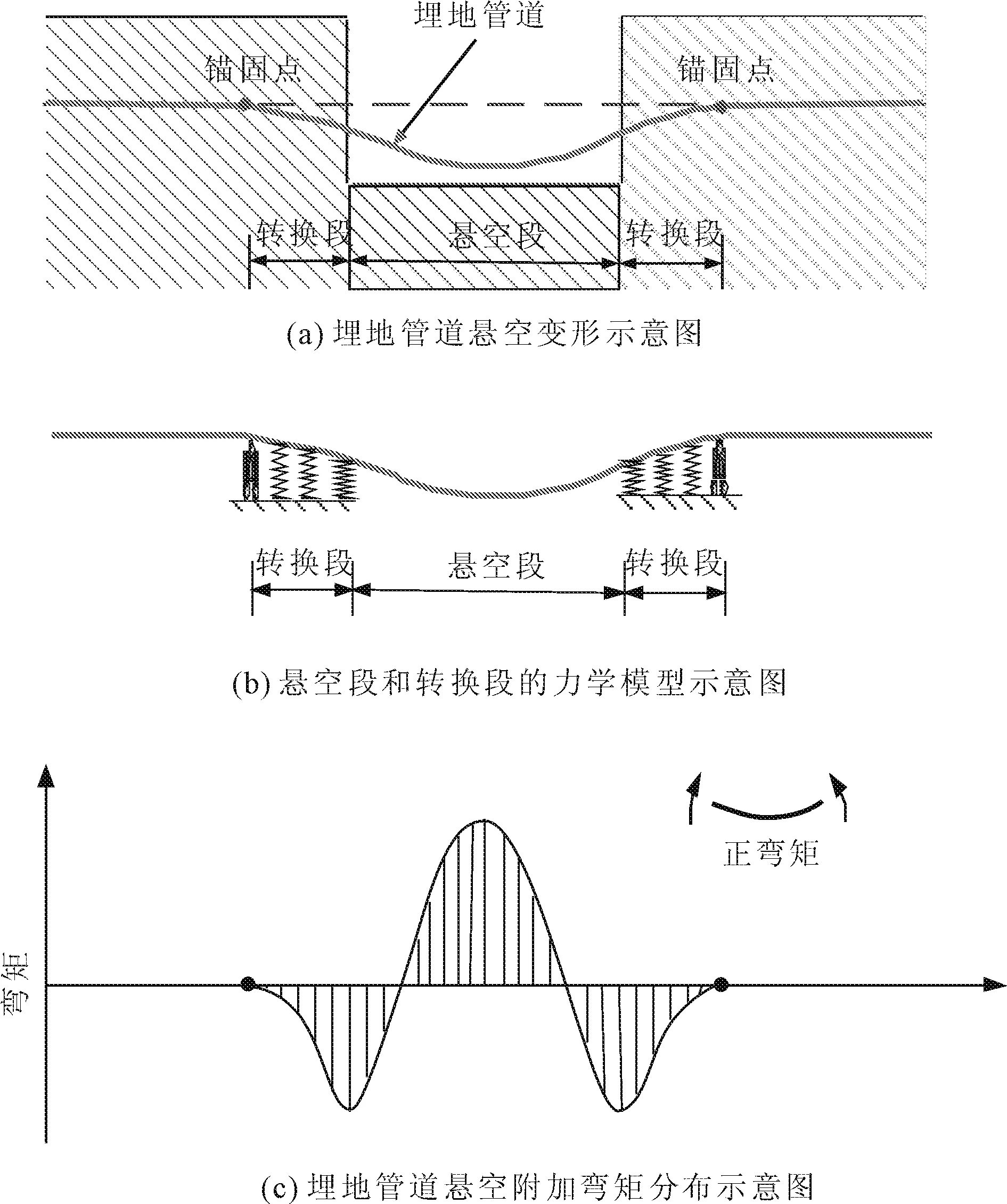
图1 埋地管道悬空变形与附加弯矩分布式示意图然
1.2 埋地管道悬空分布式光纤监测方法
上节给出了一种根据弯曲应变变化曲线识别管道悬空状态的基本原理,但是如果只对特定截面的管道进行离散式的应变监测,显然无法得到图1(c)所示的附加弯矩曲线,因此埋地管道悬空灾害监测的关键问题是获得管道的弯曲应变分布。目前,国内外较为成熟的分布式应变监测技术是基于Brillouin散射原理的分布式光纤应变传感方法,实现了埋地管道弯曲应力、整体屈曲和局部屈曲的精准识别与定量评价。
虽然管-土相互作用可以简化为Winkler地基梁模型,但是管道的变形却具有典型的三维空间特性,而Brillouin光纤传感器却只能获得一维的应变分布。为了完整获得管道的空间变形和应变分布,可采用螺旋布设和平行布设两种方式安装分布式光纤传感器,然而前者对传感器的安装位置要求极其严苛,并且布设困难、施工效率低下,后者虽然需要平行布设3条分布式光纤传感器,但是传感器均沿管道纵向布设,比较便于施工,因此本文采用这种传感器布设方式,其具体布设位置如图2所示,即在截面的12点钟、3点钟和9点钟位置分别沿管道纵向布设3条Brillouin光纤应变传感器。
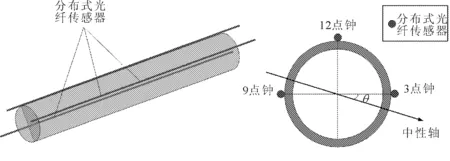
(a) 纵向 (b) 横向
沿管道纵向布设的分布式光纤传感器并不能直接得到管道的弯曲应变,测量结果是弯曲应变和轴向应变叠加的结果,并且由于施工以及管道空间变形等原因,传感器与管道中性平面之间也可能存在一定角度。针对上述问题,笔者已经建立了根据分布式光纤应变监测数据提取管道弯曲和轴向应变的方法[11-15],具体计算公式如下:
(2)
式中:x为管道纵向的任意位置;εt(x)、εL(x)和εR(x)分别为管道纵向x处截面上12点钟、9点钟和3点钟位置的传感器所获得的应变观测值;θ为管道中性平面与水平面的夹角;εb(x)和εa(x)分别为x处管道的弯曲和轴向应变。当利用图2中所示的Brillouin光纤应变传感器获得管道纵向应变数据后,即可根据式(2)完整获得管道的弯曲应变和轴向应变,进而将弯曲应变数据根据图1(c)的特征进行管道悬空状态判别。
2 模型试验
2.1 试验装置
为了验证第2部分所提方法对管道悬空灾害监测的有效性,进行了埋地管道分布式光纤监测的模型试验研究。该试验可看作是一个流动沙丘作用下管道悬空监测的小原型模拟,并不考虑严格的物理相似,仅考虑管道与土体的几何相似,着重研究悬空形成及发展过程中管道应变曲线的变化规律,重点考察分布式光纤传感器是否可以监测管道的悬空状态。
试验管道采用PPR管,长度为12 m,外径为110 mm,壁厚为15.1 mm。PPR管材的弹性模量为808 MPa,密度为910 kg/m3。在几何相似方面,以某Φ426钢管为目标,管长和径向的几何比尺分别设计为12和3.87。并且为了模拟管道和内部流体的重力效应,也对管道进行了配重。
试验在图3所示的大型管道试验箱(长12 m×宽1 m×高1.7 m)内进行,首先在试验箱内铺设厚度为1 m的碎石和土体并进行夯实,然后铺设30 cm厚的细沙,接着将管道平铺在沙床上,当完成传感器布设后在试验箱内填埋细沙。考虑流动沙丘的情况,管道上部覆沙可能已经减薄,因此埋深约为10 cm(表面至管顶),根据几何比尺换算后的实际覆沙厚度约为38.7 cm。试验中,悬空的模拟是由管道中心开挖,然后逐渐向两侧扩大,但悬跨内悬空高度一致,仅设置为3.5 cm,根据几何相似,实际悬空高度约为14 cm。需要说明,试验并未考虑悬空长度和高度的极端情况,仅为验证监测方法的可行性。
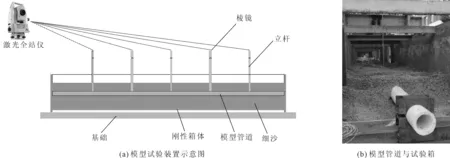
图3 管道悬空监测试验装置
按照图2所示的位置将分布式光纤应变传感器固定在管道上,同时为了进行数据比对,在管道底部增设了一条分布式光纤应变传感器,共沿管道长度方向平行布设了4条分布式光纤传感器。同时为了保证光纤监测数据的可靠性,也在模型管道的1/6、1/3、1/2、2/3、5/6长度处,在管顶和管底分别等间距布设电阻应变片。在这些位置上,也布置了轻质刚性立杆,作为管道关键断面的变形监测靶点,通过激光全站仪观测不同试验工况下管道的变形状态。
分布式光纤传感器的数据采集采用NBX-6050A光纳仪,空间分辨率设置为10 cm,距离分辨率5 cm,形成分布式的应变测量。电阻应变片的测量采用cDAQ多通道数据采集系统,应变片为1/4桥连接。管道变形采用RTS11R6 激光全站仪进行测量。
试验工况共包括8种,即以管道中点为对称中心向两侧等长度开挖,形成管道悬空。8种工况对应的悬空长度分别为1.00 m、1.50 m、2.00 m、2.50 m、3.00 m、3.50 m、4.00 m和4.75 m。
2.2 试验结果分析
根据5处全站仪监测数据,将8种工况下管道的变形情况绘于图4。可以发现,在前4种工况下,管道在悬空段及其附近区域出现了向下的挠曲变形,每种工况均为跨中挠度最大,并且随着悬空段长度增加,挠度也呈现递增趋势,但是变形数值均较小,即使在悬空长度达到2.5 m时(工况4),跨中挠度也未超过0.2 cm;在第5种工况后,跨中挠度增加明显,并且随着悬空长度的增加,挠度也不断增大,并且其影响范围也逐渐扩大;在第8种工况时,悬空长度达到4.75 m,跨中挠度达到3.5 cm,已经观察到管道触底现象。在图4中,管道挠曲变形基本以跨中为中心对称,但是实际中难以保证两侧土体约束条件完全一致,并且每种工况的开挖扰动客观存在,因此图中挠曲线的对称性也存在一定程度的偏差。
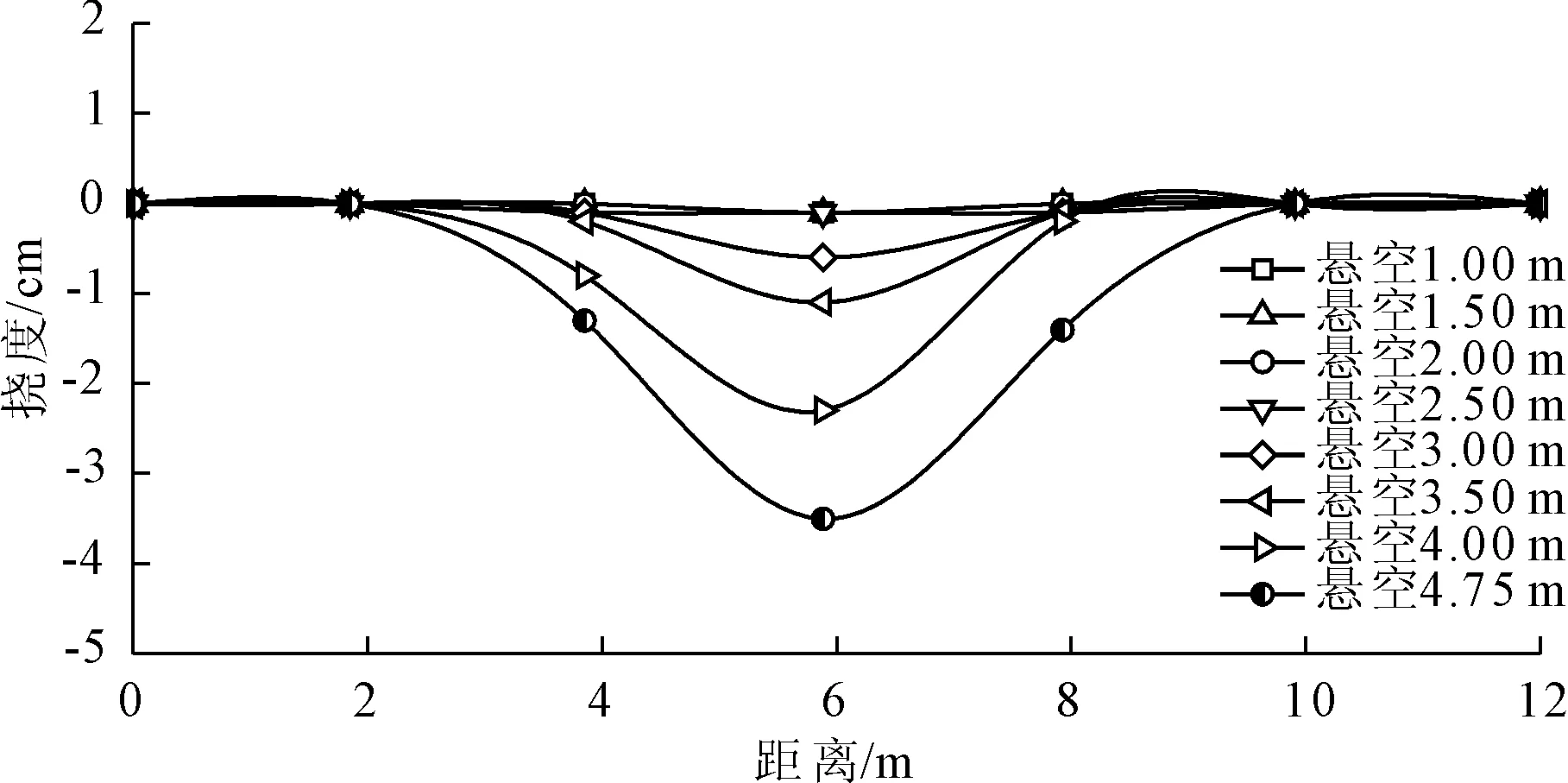
图4 不同悬空长度下管道挠曲变形监测数据
在每种工况下,都分别利用分布式光纤应变传感器和电阻应变片,监测悬空导致的管道应变变化情况。试验中,位于管道截面3点钟和9点钟的分布式应变数据分布趋势基本一致,并且数值都在±50 με范围内波动,因此认为管道轴向应变较小,数据仅与测量误差和试验扰动有关,本文限于篇幅不再列出,重点讨论与弯曲应变主导的管顶和管底的分布式应变数据(见图5)。同时,为了检验分布式应变数据的可靠性,在图5中也分别绘制了电阻应变片的测量结果。对比二者数据可以发现,所有工况中控制截面的测量结果均吻合较好,说明分布式光纤传感器可以较为精确地测量管道应变,但是如图所示,分布式光纤传感器可以获得管道任意位置的纵向应变,而电阻应变片却只能得到有限个离散测点的数据,显然无法满足管道悬空监测的需要。
图5显示,在前4种工况中,无论是管顶管底的分布式应变数据均非常小,无法明显观测到图1中的悬空特征,结合图4中的挠曲线进行分析,当悬空长度不超过2.50 m时,管道的变形较小,相对应的,管道的应变响应也应较小,因此还无法利用分布式应变数据判别管道悬空的出现。
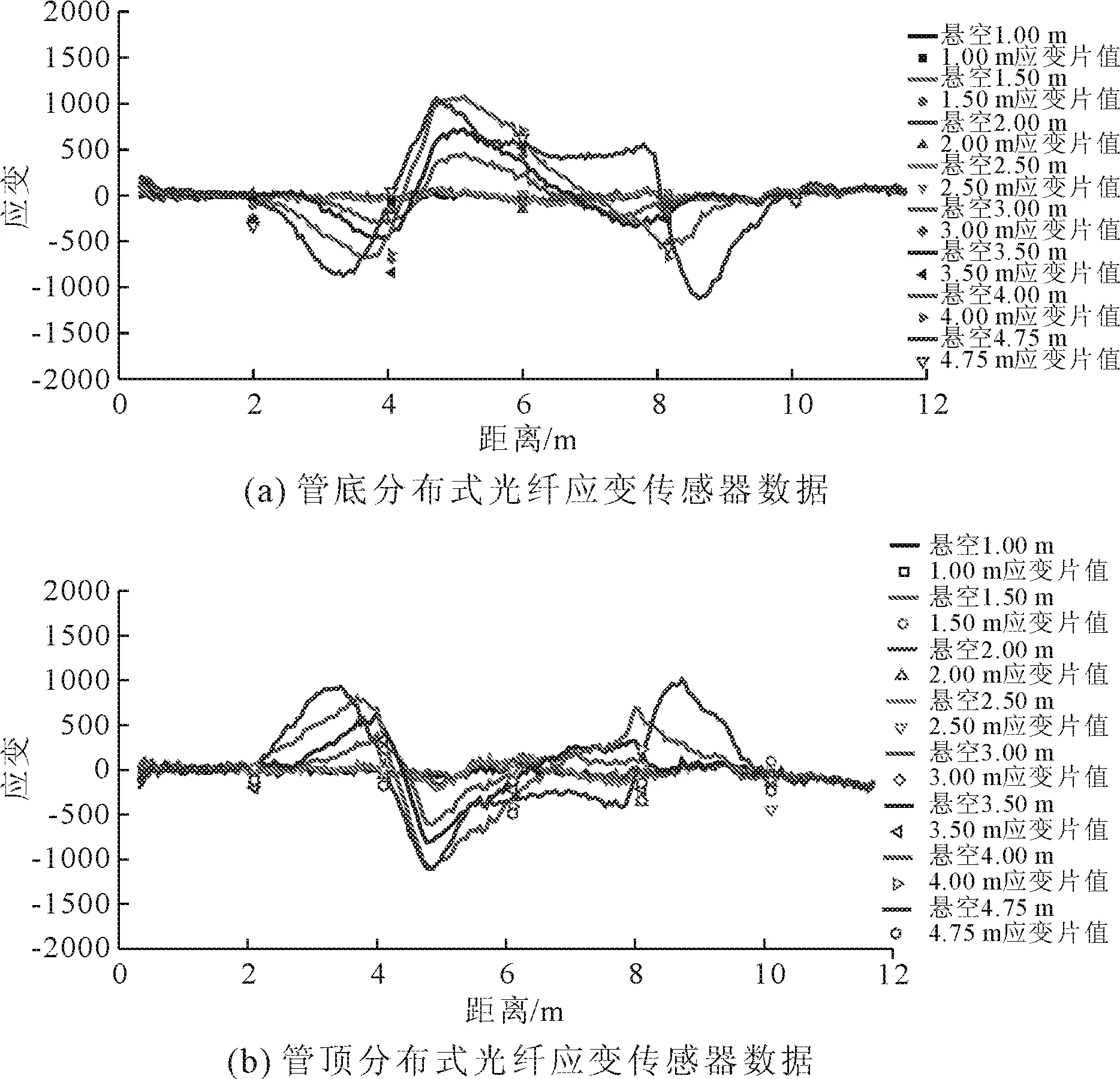
图5 不同悬空长度下管道分布式应变监测数据
当悬空长度增加至3.00 m时(工况5),图5显示管顶和管底的分布式应变数据都出现了明显的悬空特征,即在悬空段形成正弯矩(管底最大拉应变约为451 με),在悬空段两侧出现负弯矩,负弯矩逐渐增加然后减小,可判断该范围为转换段。转换段的应变在约3.00 m和9.00 m处减小为0,然后至管道两端均无应变反应,说明3.00 m和9.00 m为锚固点,悬空对其以外的区域没有影响。与实际悬空长度相比,工况5的分布式应变监测数据显示,左侧负弯矩峰值约位于4.00 m处,而左侧坡肩在 4.50 m处,右侧负弯矩峰值约位于7.50 m处,基本与右侧坡肩重合。除此以外,工况5中管道的应变分布也未以管道中点对称分布。这两种情况应与悬空两侧土体性质的非一致性、开挖扰动以及复杂的管-土相互作用有关,但是监测数据可以准确判断悬空的出现,并对悬空导致的管道应变(应力)分布给出定量结果,同时对悬空长度也可给出一定精度的估计。
随着悬空长度增加至3.50 m和4.00 m(工况6和工况7),分布式应变数据的形状都具有清晰的悬空特征,并且悬空段的峰值应变也明显增加,工况6和工况7悬空段的峰值应变分别达到716 με和1 075 με。在转换段内,负弯矩峰值对应的应变数值也逐渐增加,同时锚固点位置不断外扩。在这两种工况中,负弯矩峰值点的位置都稍位于坡肩外侧,但是差别均不超过0.50 m,说明监测数据对悬空长度的识别也基本正确。
悬空长度达到4.75 m时(工况8),图4的跨中挠度监测结果表明,管道底部已经部分触底,因此应变分布曲线不再呈现典型的悬空特征。与工况7比较,图5中悬空段峰值应变没有继续增加(1 051 με),并且在5.00 m至6.00 m范围内,其应变数值反倒明显降低,虽然6.00 m至8.00 m区域的应变数值有所增大,但是也较工况7峰值应变减小约50%,说明触底使管道悬空段的应变得到了释放和重新分布。工况8的锚固点约位于2.00 m和10.00 m处,转换段的峰值应变较工况7有所增加,对应的位置分别为3.20 m和8.60 m处,仍稍稍位于坡肩外侧,但与坡肩的偏差均不超过0.30 m,说明随着悬空长度的增加,管道下挠进一步加剧,转换段对管道提供的竖向反力不断增加,其负弯矩峰值的位置更加接近理想情况,其对悬空长度的识别更加精确。工况8的试验结果表明,所建立的悬空监测方法,不但可以准确识别管道悬空的发展,而且可以有效判断管道的触底行为。
3 结 论
流动沙丘、滑坡和侵蚀等地质灾害均可导致埋地管道发生悬空,威胁管道安全运行。实时监测管道悬空的形成与发展,可以为管道安全预警提供科学依据。根据悬空管道响应机理,提出了一种利用分布式光纤应变传感器监测悬空附加弯矩曲线的方法,建立了管道悬空的识别技术。该方法的特点是可以对管道任意位置的纵向应变进行实时监测,通过数据分析获得管道悬空的发展变化情况。模型试验结果表明:分布式光纤应变传感器与电阻应变片在控制断面的监测数据基本吻合,说明该方法对于管道纵向应变的监测具有较高的可靠性,但是却可以有效避免应变片和光纤光栅(FBG)等点式测量技术无法对管道全长任意位置进行监测的局限性;当悬空导致管道产生一定的挠曲变形后(≥6 mm),分布式光纤监测数据呈现典型的悬空特征,可以准确判断管道悬空的出现,并且根据负弯矩峰值及其消失点的位置,可以定量识别悬空长度及其影响范围(转换段);分布式光纤传感器提供了管道全长的应变分布情况,可以实时评估管道的弯曲应力状态,为悬空灾害导致的管道失效提供预警数据。为了适应实际监测评价的需求,未来应进一步研究基于人工智能的监测数据悬空特征提取方法,实现管道大范围悬空灾害的定量诊断与智能预警。

