螺旋锚极限抗压承载力理论计算分析

罗义华，石雪梅，杨泰朋，尹雪超，刘志鹏

（1.国网安徽省电力有限公司，安徽 合肥 230061；2.国网安徽省电力有限公司建设分公司，安徽 合肥 230071；3.安徽送变电工程有限公司，安徽 合肥 230022；4.安徽华电工程咨询设计有限公司，安徽 合肥 230022；5.河海大学岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098）

0 前言

近年来，在电力和通信线塔基础、输送管道基础以及建筑物基础中，螺旋锚有着越来越广泛的运用。螺旋锚承载性能优越，在承受竖向上拔荷载的作用上有着十分卓著的表现，郝冬雪等[1]开展了砂土中螺旋锚上拔承载特性模型试验研究，分析了锚盘埋深、数量、间距等因素对螺旋锚上拔承载特性的影响。郝冬雪等[2]通过数值模拟研究了黏土中螺旋锚几何尺寸对上拔承载力的影响，分析了上拔承载力随埋置深度和埋深比的变化趋势。房艳峰等[3]通过一系列相同埋深，不同锚盘间距的双锚盘螺旋锚抗拔试验，并结合对锚杆传力途径和土体破坏机理的分析推导，给出了粗砂中锚盘间距不同时双锚盘螺旋锚上拔承载力的计算方法。王杰等[4]通过室内试验对试验数据进行拟合，利用回归分析方法对试验数据进行了分析，提出了螺旋锚上拔极限承载力计算方法。王杰等[5]开展了双锚盘螺旋锚室内上拔试验，研究了双锚盘螺旋锚在砂土中的工作性能和破坏模式。王钊等[6]进行了无灌浆和灌浆FRP螺旋锚的现场拉拔试验，并基于试验结果对螺旋锚的结构和施工提出一些改进意见。苏晓青等[7]基于株洲市某基坑工程的地质条件、周边环境及基坑的设计深度，提出了螺旋锚支护方案，并对螺旋锚的抗拔承载力及支护结构进行了设计计算。刘福天等[8]开展了室内模型试验，分析了砂土中单锚片螺旋锚的工作性状及破坏模式，给出上拔极限承载力计算公式，为指导工程实践提供理论依据。王钊等[9]进行了螺旋锚的设计与制作，并开展了螺旋锚现场上拔试验，总结了螺旋锚的运行维护经验，对课题的进一步研究提出建议。螺旋锚在抗压上的表现也较为良好。针对螺旋锚竖向抗压承载特性问题，相关研究人员开展了系列研究，并取得了一些成果，董天文等[10]采用双折线数学模型，从桩身、叶片的传力路径入手，建立了螺旋锚在受压情况下荷载的传力函数；并对六根连续叶片式、分层叶片式螺旋锚的静载试验P-s曲线的拟合，证明了推导的荷载、位移可用于求解螺旋锚的P-s曲线，并可根据s-logP法判定螺旋锚的极限承载力，从而提供合理的单桩承载力设计值。张亚军等[11]分析了竖向静载荷作用下螺旋桩基础的桩土相互作用和承载性状特征，使用s-logP方法判定螺旋桩受压极限承载力。马艺琳等[12]对不同规格螺旋锚开展了现场抗压试验，通过将所绘制的Q-s曲线进行对比研究，发现叶片直径、桩径、叶片个数以及降水情况对螺旋锚极限抗压承载力均有一定影响。Guo等[13]基于小尺寸螺旋锚开展了现场静载荷试验，提出当位移达到锚盘直径的十分之一时，螺旋锚达到极限状态，此外基于建立的理论模型对螺旋锚安装扭矩进行了估算。Guo等对循环荷载作用下螺旋锚的位移情况进行现场量测，发现位移幅度与锚盘直径以及锚长有关，并随着锚盘直径与锚长的增大而减小。马艺琳等[12]开展了现场试验对螺旋桩抗压承载力进行了研究，并分析了叶片直径、叶片个数、桩径以及降水情况对螺旋桩承载特性的影响。

综上可知，目前针对竖向下压荷载作用下螺旋锚的承载力理论计算方法方面的研究仍相对较少，因此，本文拟基于极限平衡原理，给出螺旋锚竖向抗压达到极限状态时的土体破坏模式假定，并基于此推导螺旋锚抗压极限承载力理论计算公式。通过与现场试验实测值的对比分析，验证本文所建立理论模型的准确性和可靠性。续而，分析锚盘直径、锚杆直径等因素对螺旋锚极限抗压承载力的影响规律。

1 理论模型的建立

1.1 基本假定

本文计算螺旋锚单锚抗压极限承载力时将锚盘间的土体破坏面假定为圆柱形剪切面，该假定仅在锚盘间距不过大时适用（锚盘间距小于3D）。在该假定下，螺旋锚抗压极限承载力可分为螺旋锚钢管与土体之间的摩阻力、锚盘之间圆柱形剪切面上的剪应力以及最下层锚盘的“端阻力”。其中，计算桩土间摩阻力以及圆柱形剪切面上的剪应力时使用β法计算；计算最下层锚盘的“端阻力”时将其假定为直径与锚盘直径（D）相等的等截面桩计算，具体受力如图1所示。

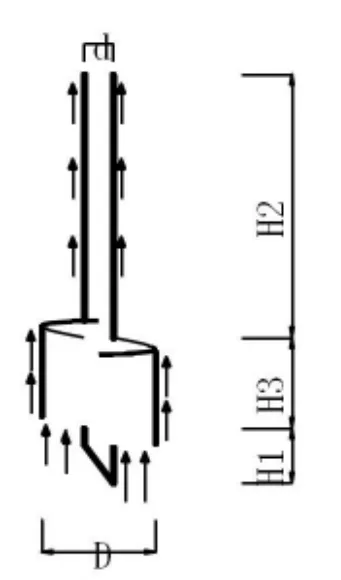
图1 竖向下压荷载下螺旋锚单锚受力图

1.2 控制方程和公式推导

螺旋锚受压极限承载力：

其中，T1为螺旋锚钢管与土体之间的摩阻力；T2为锚盘之间圆柱形剪切面上的剪应力；T3为最下层锚盘的“端阻力”。

T1采用β法计算，即：

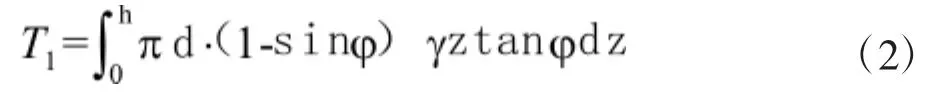
其中，h为螺旋锚入土深度，φ为土体内摩擦角。T2亦采用β法计算，即：

最下层锚盘所产生的端阻力T3按直径与锚盘直径D相同的等截面桩确定，即：

其中，N为待定参数，当 D＞60cm时，N=6；当30cm＜D＜60cm时，N=7。Cu为土的不排水抗剪强度。综上，螺旋锚单锚极限抗压承载力：

当锚盘数为1时，可视作多锚盘的特殊情况，即T2=0，T1和T3计算方法不变。

2 理论模型的验证与分析

2009年，董天文等[14]在滨海冲积平原进行了螺旋锚单锚的竖向上拔试验，本文引用其数据对上述公式进行验证。

试验场地为滨海冲积平原，场地平整。地下水位4.5 m，地层从上到下依次为：①耕植土，由黏性土颗粒组成，可塑到流塑状态，厚度0.5 m。②粉质黏土，厚0.7 m，平均含水率47.18%，比重为2.69，湿密度为1.63 g/cm3，天然重度 15.97 kN/m3，饱和度 88.63%，液限为38.87%，塑限为22.25%，压缩模量为1.30 MPa，黏聚力为9.33 kPa，内摩擦角为2°。对土层信息进行提炼，即土体粘聚力8～11 kPa，内摩擦角2°，抗剪强度为80 kPa。

螺旋锚钢管和锚盘材料均为钢材Q235，锚盘数均为3个，端部为锥形铸铁墩头。本文选取两根螺旋锚对公式进行验证：螺旋锚1桩径0.14m，桩长5.4m，叶片直径0.708m，叶片间距1.5m；螺旋锚2桩径0.14m，桩长6.95m，叶片直径0.65m，叶片间距1.5m。

通过所推理论公式计算得螺旋锚1极限抗压承载力约为228.5kN，而现场试验得到的极限抗压承载力为245.7kN，偏差约7.0%；螺旋锚2极限抗压承载力约为225.3kN，而现场试验得到的极限抗压承载力为205.1kN，偏差约9.8%。算例参数及计算结果列表分别见表1和2所示。由表2可知，根据所推公式计算的两根螺旋锚的受压极限承载力偏差均在10%以内，因此可初步认定本文所假定的破坏模式接近实际破坏情况，所推导的理论计算公式可用于螺旋锚工程设计中的受压极限承载力估算中。但由于算例不够充足，数据较少，后续仍需开展试验进行进一步验证。

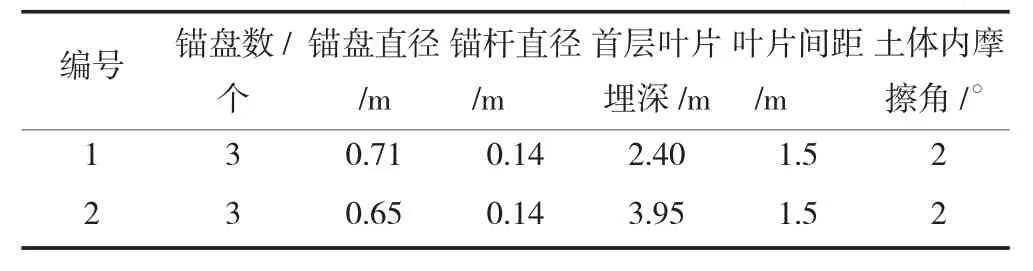
算例参数 表1

极限抗压承载力计算与实测结果对比 表2

3 影响因素分析

3.1 锚盘直径的影响分析

为了探讨竖向下压荷载作用锚盘直径对螺旋锚极限承载力的影响，取锚杆直径0.2m，螺旋锚总长4m，土体重度 16 kN/m3，内摩擦角 2。，锚盘数为 2，首层叶片埋深取2.5m，锚盘直径0.3～0.6m，间隔0.05m选取。通过上文所述公式对螺旋锚抗压极限承载力进行计算并绘制抗压极限承载力和锚盘直径之间的关系曲线如图2所示。

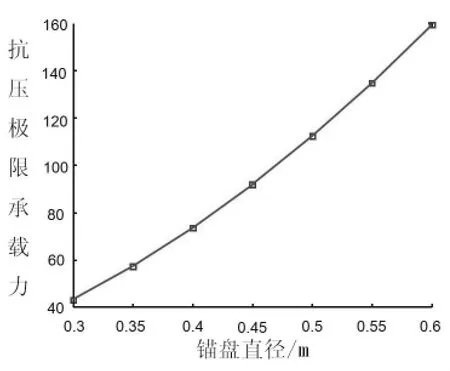
图3 锚杆直径对极限抗压承载力影响规律

由图2可知，在其他条件相同且锚盘直径不过大的情况下，随着锚盘直径的增大，螺旋锚抗压极限承载力呈上升趋势，且近似呈线性增长。

3.2 锚杆直径的影响分析

为了探讨竖向下压荷载作用锚杆直径对螺旋锚极限承载力的影响，取锚盘直径0.6m，螺旋锚总长4m，土体重度 16 kN/m3，内摩擦角 2。，锚盘数为 2，首层叶片埋深取2.5m，锚杆直径0.2～0.3m，间隔0.01m选取。通过上文所述公式对螺旋锚抗压极限承载力进行计算并绘制抗压极限承载力和锚杆直径之间的关系曲线如图3所示。由图3可知，在合理范围内，随着锚杆直径的增大，螺旋锚抗压极限承载力呈上升趋势。锚杆直径对螺旋锚抗压极限承载力影响较小，基本可忽略不计。

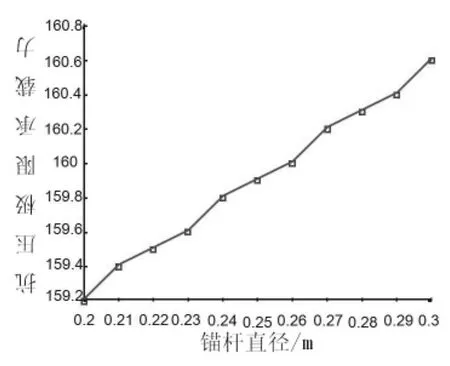
图2 锚盘直径对极限抗压承载力影响规律

4 结论

本文基于极限平衡原理建立了竖向下压荷载作用下螺旋锚的极限抗压承载力理论计算方法，并分析了锚盘直径和锚杆直径对螺旋锚抗压承载特性的影响规律，可以得到如下结论：

①尽管本文理论模型建立时的基本假定有一定的局限性。但是，本文所建立的理论模型与实际破坏情况较为符合，通过两个算例的验证初步认为所推导的理论计算公式可用于工程实际对螺旋锚单锚抗压极限承载力的估算中，但后续仍需开展相关试验进行进一步验证。

②在破坏面形式不变的情况下，螺旋锚抗压极限承载力随锚盘直径的增大而增大，且变化基本呈线性。随着锚杆直径的增大，螺旋锚抗压极限承载力也有一定的增长，但增长较小，可认为锚盘直径是影响螺旋锚抗压极限承载力的主要因素之一。