预应力混凝土桥梁施工监控应力修正及应用分析

周戈，盛光祖，李浩然

（1.武汉地产开发投资集团有限公司，武汉430022；2.防灾减灾湖北省重点实验室（三峡大学），湖北 宜昌443002）

1 引言

为了成桥线形和内力满足设计要求，悬臂浇筑的大跨度预应力混凝土桥梁常会埋设振弦式应变仪器，实时监控关键截面的主梁应力[1]。但随着桥梁跨度的不断增大，施工荷载、混凝土收缩徐变以及环境温度的影响也愈发明显，悬臂施工的梁段应力变得较为复杂，造成监测的结果与实际应力存在较大误差。如何剔除测量应力中混凝土收缩徐变、温度等因素的影响，对施工中的梁段实测应力进行准确修正，以便掌握主梁应力真实变化显得十分必要。

目前，国内外许多学者对大跨度桥梁施工中应力监测的影响因素及应力修正的方法展开了广泛研究。Praja[2]研究了蠕变和收缩对大跨度桥梁结构中的应力分布的影响。文献[3]分别采用不同的预测模型，对混凝土的收缩、徐变进行计算并对比分析。Baleviˇcius 等[4]提出了混凝土黏结、收缩、蠕变和老化对加载后预应力混凝土构件应力-应变状态和抗裂性能影响的分析和数值模型。Singh 等[5]研究了混凝土的时变和可变弹性模量对桥梁结构的影响，并对比分析了3 种不同弹性模量模型，发现随混凝土龄期变化的弹性模量会影响应力的计算结果。文献[6]研究了依时间荷载变化的粉煤灰混凝土弹性模量对徐变的影响。叶雨山等[7]利用现场应变和温度测试结果，对温度修正系数和收缩应变进行修正。文献[8]基于振弦式应变计测试原理和现场试验的方法，分析了环境温度、水化热及太阳辐射对测试结果的影响。文献[9]根据所观测的温度数据，取用最不利时刻温度进行温度分布曲线的拟合。对比分析实测值和理论值的差异。Faravelli 等[10]以某铁路桥为例，分析了随温度变化结构响应的变化规律。Krkoška 等[11]分析了混凝土箱梁桥的热负荷概况。对平衡悬臂法实现的混凝土箱梁桥横截面真实温度梯度的测量进行了分析。针对监测的应力数据处理方法，文献[12]基于最小二乘法原理对应力理论数据、实测数据进行曲线拟合，得到各施工阶段的应力状况。胡海军等[13]结合小波多层滤波和FFT 低通滤波对应变监测数据进行降噪处理，提出了一种能有效消除数据噪声，从而提高数据准确性的新方法。

上述研究为预应力混凝土桥梁施工监测应力的修正奠定了坚实的基础。传统实测应力修正方法是将混凝土收缩徐变、温度变化引起的应变值从实测总应变中剔除和修正。混凝土收缩徐变产生的应变计算是依据JTG D62—2012《公路钢筋混凝土及预应力混凝土桥涵设计规范》，综合考虑龄期、混凝土种类、湿度和构建理论厚度对收缩徐变应变值的影响，计算混凝土梁的收缩徐变应变。但是，上述实测应变修正方法首先忽略了大跨度桥梁分节段悬臂施工时荷载逐步施加对徐变的影响，其次未考虑混凝土弹性模量随龄期发展的特性，会导致修正过后的应力值仍然与理论值差距较大，不能准确地反映施工过程中结构的真实应力状态，不利于有效、准确地进行桥梁施工控制工作。因此，本文提出一种大跨度预应力混凝土悬臂施工桥梁主梁应力修正方法，其特点是考虑大跨度预应力混凝土桥梁分节段施工时荷载逐步施加，构建分段应力增量下的混凝土徐变计算公式，利用加载龄期至计算龄期的等效弹性模量替换传统计算用的不变弹性模量，克服传统应力修正方法的缺陷。

2 主梁监测应力修正方法

预应力混凝土桥梁采用悬臂浇筑法施工时，主梁的悬臂端无约束，混凝土收缩徐变、温度变化以及初始应变将使主梁产生无应力应变，所以，需要将无应力应变从实测总应变中分离、剔除、修正，再乘以弹性模量，才能获得主梁的真实弹性应力。在桥梁悬臂施工的某一节段，应变传感器采集时刻t时的混凝土总应变ε（t）可分解为：

式中，εi（τ）为t时刻主梁真实弹性应变；εc（t）、εcs（t）、εT（t）分别为某时刻t徐变引、收缩和温度变化引起的应变值；ε0为初始应变，包括应变计钢弦初始拉应变和混凝土初始应变。

2.1 混凝土徐变产生的应变

传统徐变计算方法是通过老化系数，建立徐变与加载时初应变的关系：

式中，φ（t，t0）为徐变和系数。计算徐变产生的应变时，忽略了结构悬臂施工时荷载逐步施加对徐变的影响，另外，也未考虑混凝土弹性模量随龄期发展的特性，因此徐变计算误差较大。

大跨度桥梁分节段悬臂施工时，荷载也随主梁节段施工逐步增加，所以主梁的真实应力是呈阶梯式趋势增加。主梁应力增长规律如图1 所示。

图1 分阶段施工应力变化示意图

由混凝土线性徐变理论可知，当混凝土工作应力小于混凝土强度50%时，徐变应变与所施加的应力具有线性关系，而一般工程混凝土的工作应力都在该范围内。结合鲍尔茨曼（L.Boltzman）叠加原理可知，时间t内徐变应力作用下的总应变，为每一应力增量引起的应变总和。

基于上述2 个理论，在计算龄期t内总徐变应变时，不考虑应力历史，将分阶段变化的应力离散为单个互不影响的应力增量，再分别计算不同龄期加载的应力增量产生的徐变应变，即：

由此可推导出龄期ti内各应力增量产生的总徐变应变为：

式中，εc，i为混凝土龄期ti时徐变应变值；t0、ti、tj分别为工况0、i、j完成后混凝土龄期；σ0为加载时初应力值；E（t0，ti）为龄期t0至龄期ti的混凝土等效弹性模量；φ（t，t0）为加载龄期t0至计算龄期ti的混凝土徐变系数；Δσj为第j个工况施加的应力增量；E（tj，ti）为龄期tj至龄期ti的混凝土等效弹性模量；φ（ti，tj）为加载龄期tj至计算龄期ti的混凝土徐变系数。

参考国内关于徐变系数的最新规范JTG D62—2012《公路钢筋混凝土及预应力混凝土桥涵设计规范》[14]，徐变系数按式（7）计算：

式中，φ0为考虑湿度、混凝土强度、加载龄期影响的名义徐变系数；βc为加载后徐变随时间的发展系数。名义徐变系数计算时可参照规范取值。

普通混凝土在正常浇筑情况下，其弹性模量会随时间发展而逐渐增加，如果取弹性模量为一定值，那么必将影响徐变应变与结构真实弹性应力的计算结果。目前，与混凝土龄期有关的弹性模量计算模型主要有2 种，美国规范ACI 认为弹性模量的发展和强度相关，但该公式不能回推出28d 弹性模量，还有待改善。欧洲规范CEB-FIP（1990）[15]给出的时变弹性模量预测模型考虑了混凝土种类和龄期的影响，同时满足了随时间发展，弹性模量增加，趋于一个极限值，并且可以回推出28d的弹性模量，公式应用便捷准确，且对国内普通混凝土也有很好的适用性。因此，利用式（6）计算徐变应变时，采用该时变弹性模量公式：

由于龄期tj到龄期ti内混凝土弹性模量连续变化。在计算该龄期范围内施加的应力增量所产生的徐变应变时，弹性模量不方便取值。于是在这里引入等效弹性模量E（tj，ti）。

E（t）在龄期范围内为连续函数，满足积分中值定理，显然有：

从而得到龄期tj至龄期ti混凝土的等效弹性模量为：

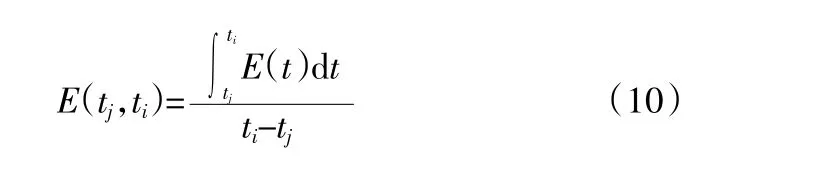
2.2 温差引起的应变值

振弦式传感器通过感知应变筒中钢弦自振频率的变化而得出应变。在温度变化时，由于混凝土和钢弦的线膨胀系数不同，二者为了保持变形协调产生约束力，使得钢弦初始频率改变，从而导致读数误差。温度变化导致的应变误差可按式（11）计算：

式中，α为混凝土线膨胀系数，取1×10-5℃-1；β为钢弦线膨胀系数，取1.22×10-5℃-1；T为时刻t应变计所测得温度；T0为应变计所测得初始温度。

2.3 混凝土收缩引起的应变值

混凝土收缩可按照JTG D62—2012《公路钢筋混凝土及预应力混凝土桥涵设计规范》计算：

式中，εcs（t，ts）为混凝土龄期t内的收缩应变；ts为混凝土收缩开始时的龄期，一般取3～7d；εcs0为名义收缩系数；βs为收缩随时间发展的系数；h为构件理论厚度；h0、t1为常数。

2.4 实测应力修正

根据式（6）、式（11）和式（12），可分离和剔除收缩徐变、温度变化以及初始应变的影响，则大跨度预应力混凝土桥梁在悬臂施工过程中主梁真实弹性应力为：

根据上述思路，构建了主梁实测应力修正方法，如图2所示。

图2 应力修正步骤流程图

3 工程应用

3.1 工程概况

南龙铁路双洋大桥位于福建省漳平市双洋镇，当地年平均相对湿度为70%。该桥是一座3 跨预应力混凝土双线连续箱梁桥，跨度布置为40.6m+64m+40.6m。主桥立面布置如图3 所示。全桥分为2 个T构，采用挂篮悬臂浇筑法对称施工，主梁用C50 混凝土浇筑，每个T 构每边包括0～8 共9 个梁段，2 个边跨各有7.6m 的现浇段，边跨合龙段2.0m，中跨合龙段2.0m。上部结构为单箱单室斜腹板变截面箱梁。全桥共布置11 个应力测量截面，分别位于2 个T 构的悬臂端部、边跨1/4 跨径、边跨1/2 跨径、中跨1/2 跨径及中跨合龙段处，每个测量截面的顶、底板各埋设3 个振弦式传感器。施工阶段共划分为38 个工况，每个主梁节段施工包括：挂篮前移、混凝土浇筑、预应力钢束张拉3 个工况。采用空间有限元软件Midas Civil建立双洋大桥有限元模型，计算每节段主梁理论应力。

将上述修正方法应用于双洋大桥实际工程中，对施工过程中实测的应变数据进行修正、分析。该方法步骤较多，且需要循环计算，手算较复杂也容易出错。笔者运用MATLAB 数学软件编写相关程序，实现了该方法的计算机算法，大大减少了数据处理分析的时间，也提高了算法的准确性。

3.2 应力对比分析

为了验证本文方法的准确性，选取了桥4 号墩0#块小里程梁体顶部17 个工况，计算了主梁应力修正值，并与传统应力修正值、理论应力值对比。17 个工况对比值如表1 和图4 所示。

表1 4 号墩0#块小里程箱梁顶部应力对比表

图3 双洋大桥主桥立面及0#块传感器布置图

图4 4 号墩0#块箱梁顶部应力对比图

由表1 可知，工况1 时，箱梁顶面应力理论值是-0.61MPa，实测应力值为-1.66MPa，传统修正应力值为-1.21MPa，本方法修正应力值是-1.13MPa。随着桥梁施工节段的增加，工况17时，箱梁顶面应力理论值是-7.38MPa，实测应力值为-11.97MPa，传统修正应力值为-9.33MPa，本方法修正应力值是-7.02MPa。

由图4 可知，实测应力值与理论值偏差最大，传统修正值的偏差减小，但采用本方法修正后的应力值与理论值吻合最好，误差显著降低，验证了该修正方法的可靠性与准确性。随着桥梁节段工况的增加，实测应力值和传统修正值的偏差越来越大，应力累计误差也越来越大，而本方法修正值与理论值偏差相对稳定。

利用该方法对双洋大桥悬臂施工过程的主梁测量应力进行了修正计算，桥梁顺利合龙，达到了施工和设计预期。

4 结语

本文提出了悬臂施工的大跨度桥梁监测应力修正方法，并将该方法应用于某大跨度箱梁桥的应力监控工作中。结论如下：

1）混凝土桥梁在悬臂分段浇筑时，主梁应力随施工工况而改变，建议计算徐变应变时宜按应力增量引起的变形进行叠加计算；

2）混凝土弹性模量随龄期发生改变，早期尤为明显，对结构应力计算的影响较大，应该考虑弹性模量变化的问题；

3）本文修正计算方法准确可靠，能有效修正徐变效应产生的无应力应变，可为今后桥梁施工控制中的监测应力修正提供参考；

4）预应力混凝土桥梁施工应力监测过程中，影响因素众多，实测应力误差较大，施工控制中有必要对应力误差进行准确分析。