竖井纵向位置对隧道自然通风的影响

王 文 孙三祥 陈军强

竖井纵向位置对隧道自然通风的影响

王 文1孙三祥2陈军强3

（1.陕西铁路工程职业技术学院 渭南 714000；2.兰州交通大学环境与市政工程学院 兰州 730070；3.铁道第一勘察设计院新疆分院 乌鲁木齐 830011）

隧道竖井自然通风在长大隧道运营通风中的作用不可忽视，故竖井位置的选择也很重要。研究基于FLUENT软件，采用RNG湍流模型，对单一竖井在隧道不同纵向位置通风换气结果进行三维数值模拟，得出竖井位于隧道纵向不同位置时隧道内风速及流场分布规律。计算出竖井在不同纵向位置时隧道整体完成一次通风换气所需时长，通过拟合得出竖井位置与通风换气时长呈指数关系，为长大隧道设计、建设过程中竖井位置的选取和通风方式的确立提供参考。

自然通风；竖井；流场；数值模拟

0 前言

目前，国内外对隧道竖井通风的研究主要集中在机械通风和隧道防排烟方面，对于隧道竖井自然通风对隧道运营通风的研究较少。薛运祝[1]将硖石上行隧道的实测资料，加以整理，利用其排烟规律，分析竖井对隧道自然通风的影响。朱杰等[2]利用小尺寸竖井模型进行系列试验，分析不同竖井侧向开口位置对烟囱效应的影响程度。李志伟等[3]采用数值计算方法，对高速列车通过有竖井的隧道时其瞬变压力进行模拟。冯炼等[4]基于越江隧道实际，采用一维模型对公路隧道气流流动与污染物浓度分布规律进行模拟计算。杨伟超[5]等采用数值模拟方法，对有无竖井条件下列车高速通过隧道时车体压力的变化过程进行模拟，研究竖井对车体压力的作用机理。王峰等[6]考虑通风竖井对地铁内热湿环境及压力变化的影响，进一步优化地铁内竖井的位置。Zhu等[7]讨论和分析了当前在中国特长隧道运营通风的能耗状况，提出超长分段隧道自然风能利用的方法。G Tamm等[8]对竖井压力和浮力引起的热气体流动进行了实验研究。Ji等[9]通过一系列的燃烧试验，研究了竖井高度对城市道路隧道火灾自然通风的影响。Li等[10]研究了热压对斜坡隧道通风的影响，并基于温度下降的指数模型，提出了倾斜地下隧道热压力预测方程。Fan等[11]通过大涡模拟（LES）研究了竖井上方环境风对隧道自然通风效果的影响，通过系统地改变竖井上方的环境风速和隧道纵向风速，对烟气运动特性进行了详细研究。

本文依托于某在建高海拔单洞单线铁路隧道工程实际，运用数值模拟软件Fluent，采用RNG-湍流模型，对不同竖井布置方式下隧道内流场及通风换气时长进行模拟分析，并总结出可供参考的一般性规律，为隧道运营通风环境改善、节能及竖井选取提供参考建议。

1 基本计算理论

隧道内自然风的影响因素主要有三部分：（1）隧道洞口间的大气压梯度产生的超静压差；（2）隧道内外温差产生的热压；（3）洞外自然风产生的动压。

1.1 无辅助坑道隧道等效压差计算

（1）超静压差

图1 隧道超静压差、热位差示意图

如图1所示，超静压差可按照以下方程计算：

式中：1、2为两洞口的压力，0为洞内的空气密度，kg/m3。

（2）热位差

隧道热位差产生的原因是由于温度变化而导致隧道洞内外密度发生变化。热位差计算公式为：

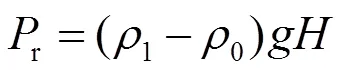
式中：1、0分别为洞外和洞内的空气密度，kg/m3。

（3）洞外自然风动压

洞外气流的动压是在两洞口超静压差作用下进入隧道的气流所带入的动能，其计算方法为：

式中：a为洞外自然风速，m/s。

公式（1）（2）（3）的和可理解为形成洞内自然风的动力，称为等效压差n，又等效压差与自然风在隧道内流动过程中的阻力(压头损失)相等，即：

式中：为隧道沿程阻力系数；为隧道的长度，m；为隧道局部阻力系数；n为隧道内的自然风速，m/s。

于是公式（5）可写成：

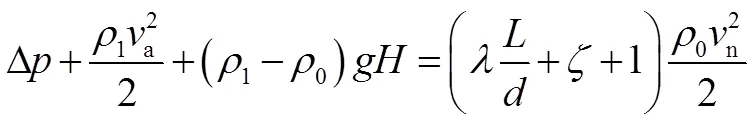
上式说明隧道内自然风的等效压差n与隧道内自然风速n相关。

1.2 带辅助坑道隧道等效压差计算

对于分段式纵向通风的隧道，其辅助坑道有竖井、斜井等。其等效压差的计算与无辅助坑道时的原理相同，等效压差仍然由两洞口的超静压差、洞内外温差产生的热压和洞外气流的动压组成。以单一竖井为例，可按照两个循环回路计算。

（1）超静压差

如图2所示，以竖井口4为基准点，△4=0、1、2、3处基于4的超静压差分别为△1、△2、△3。当风流达到稳定时，3处全压力为△′3，当风流口流入节点3时为正，流出为负。根据风流流动的阻力定律有：

式中：=(1,2,4)；为第个风道的风阻，R=λρ/8×LC/A3。其中，λ为沿程阻力系数，L为风道长度，C风道断面周长，A为风道断面面积，R为风道的入口局部风阻。

对于节点3有：

式（6）和式（7）组成的方程组为非线性方程组，求解方程组。△P′3=min(△P1，△P2，△P3)，分别对Qi计算，当∑Qi＜ε时（ε为求解的控制精度），Qi即为方程的解，即可求出vi。

（2）热位差的计算

如图3所示，单竖井通风时的隧道热位差可按两个循环回路计算。

式中：△Pr1，△Pr2分别为1与4处、2与4处之间的热位差，ρr1=(ρ1+ρ4)/2，ρr2=(ρ2+ρ4)/2，ρ1、ρ2、ρ4分别为隧道入口、出口和竖井口的空气密度，kg/m3。

有竖井时洞外自然风压的计算与无辅助坑道自然通风的计算方法类似。

空气容重根据下式计算：

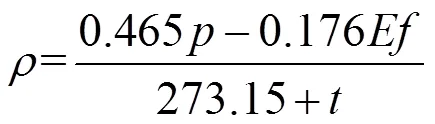
式中：为空气密度，kg/m3；为大气压，mmHg；为温度，℃；为温度时的饱和水汽压，mmHg；为空气的相对湿度。

2 模型建立

2.1 物理模型

依托某在建高海拔单洞单线特长铁路隧道工程实际，利用CFD软件建立三维隧道模型。考虑到竖井对隧道影响的区域有限，简化模型，取隧道模拟长度为3000m，隧道两洞口无高差，建立七种隧道三维模型。模型1：隧道长为3000m的无竖井隧道。模型2~6：为3000m的带竖井隧道，竖井位置分别位于距隧道计算入口1=500m、1000m、1500m、2000m、2500m横通道上方。模型7：隧道长为3000m的带竖井隧道，竖井位置位于距隧道计算入口1500m隧道正上方。竖井直径为3m，高200m。隧道模型示意图如图4所示。

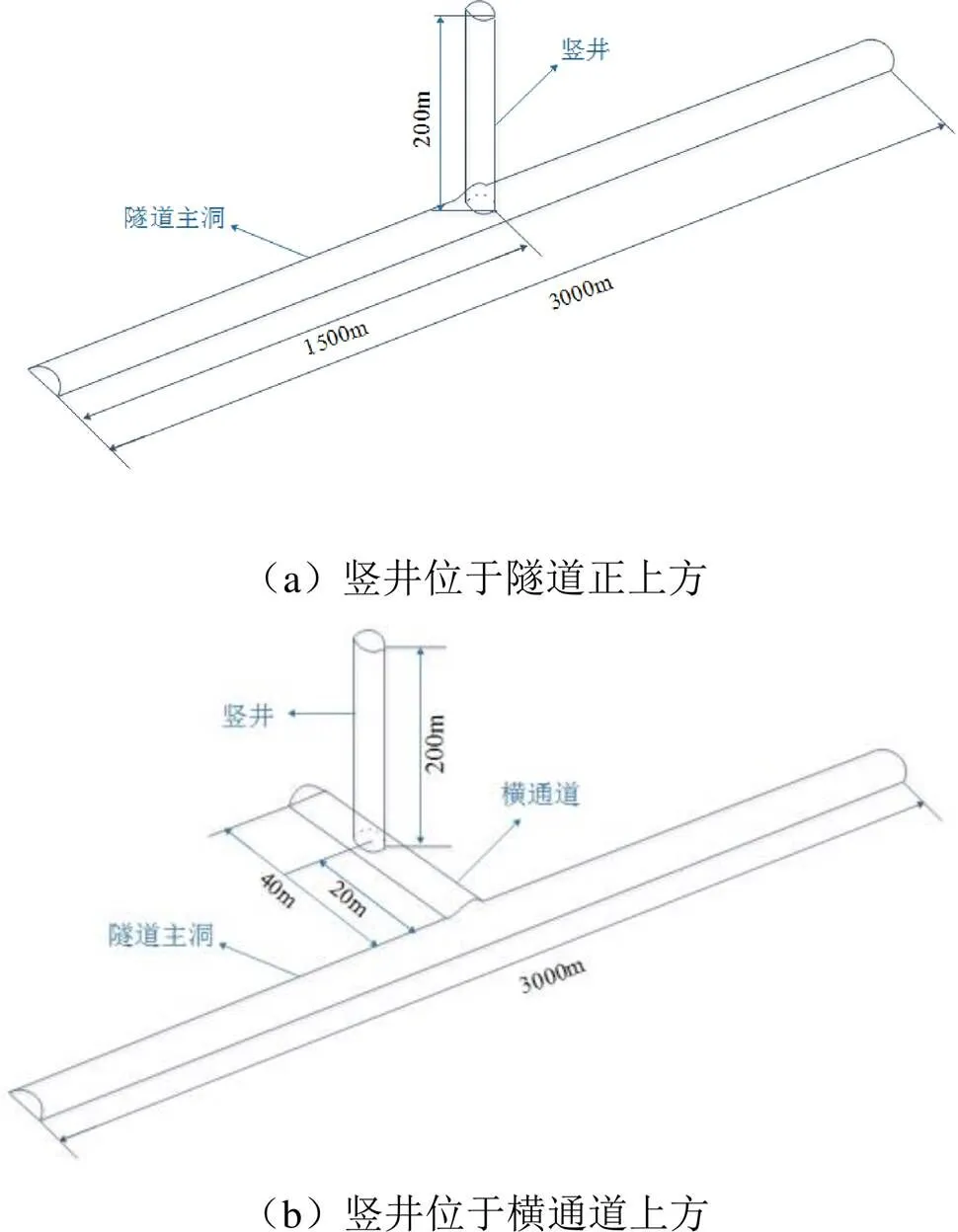
图4 计算模型示意图

2.2 边界条件设置

根据现场实测，取隧道气压平均值为70kPa，隧道外气温为20℃，隧道内气温为15℃，平均相对湿度为25%，洞外自然风速取a=2.6m/s。由式（9）可计算出隧道内空气密度0=0.845kg/m3、隧道外的空气密度1=0.83kg/m3。

（1）入口边界：隧道入口采用压力入口边界。

（2）出口边界：隧道出口采用压力出口边界。

模型1由式（2）、（3）可计算出两洞口的热位差和洞外自然风动压。模型2～7隧道由式（3）、（8）可分别算出隧道两循环回路的热位差及隧道外自然风产生的动压。参考文献[12]取山前正压为+0.92/2，山后负压为-0.32/2，山顶负压为-0.62/2计算两洞口超静压差。

（3）壁面边界：隧道壁面设为无滑移、绝热边界条件，粗糙度根据规范设为0.008m。

计算得出，无竖井隧道等效压差n=6.2Pa；单竖井隧道，回路1隧道等效压差n=37.53Pa，回路2隧道等效压差n=34.16Pa

3 数值算法及模拟验证

3.1 数值计算方法

隧道流场计算采用定常隐式解法，选取RNG湍流模型，流场迭代采用SIMPLE算法，离散格式采用二阶迎风格式，考虑浮力的作用。利用Gambit软件对模型进行网格划分，根据模型特点，选择分区划分方式，采用六面体和四面体网格对模型进行网格划分。模型1的网格总数为423 000；模型2～7将竖井前后20m区域网格做加密处理，各模型网格数约为45万，并进行了网格无关性检测，确保模拟结果与网格数量无关。

3.2 模拟结果验证

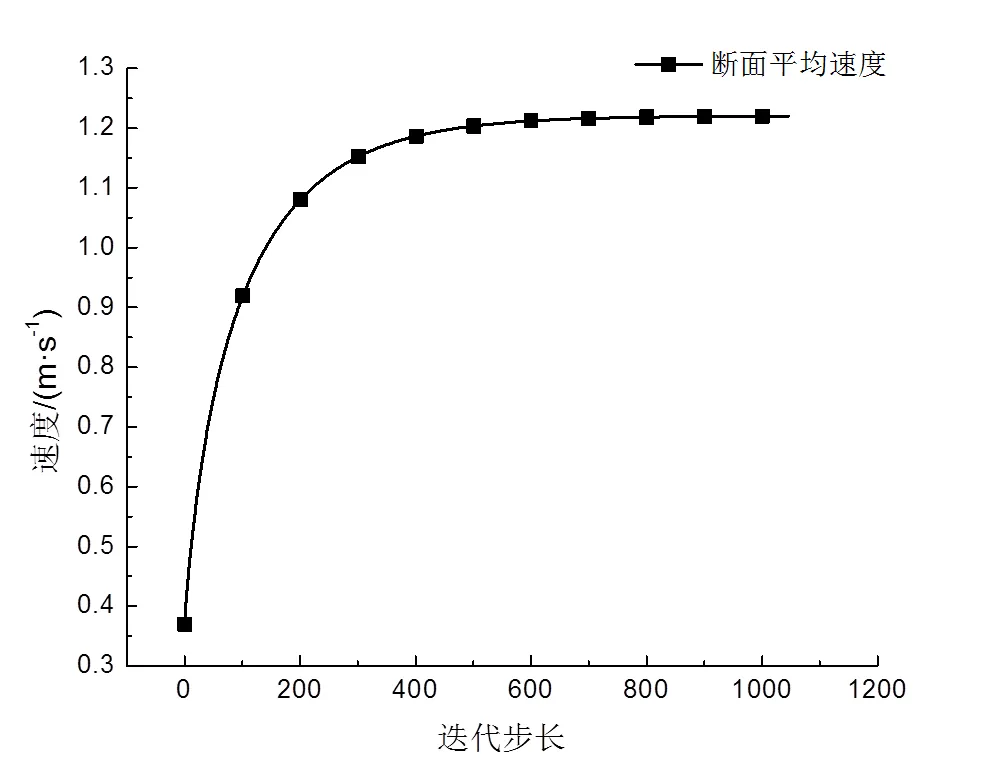
图5 隧道出口断面监测速度

对无竖井隧道进行三维数值模拟，模拟计算洞内、外温差为5℃时隧道内流场的分布情况。将隧道出口断面设置为监测面，监测隧道出口断面平均速度，结果如图5所示。

由图5可以看出，速度稳定时，隧道内的自然风速为n=1.225m/s。隧道的主要参数如表1所示。

表1 隧道主要参数

由公式（4）得出隧道内的自然风速计算公式为：

结合表1的数据，由公式（10）计算出隧道内的自然风速为n=1.14m/s。

表2 计算结果与模拟结果比较

由表2可以看出，隧道内外温差为5℃时，计算结果和模拟结果误差可以控制在7%以内，结果吻合较好。此结论验证了模拟计算的正确、可行性。

4 模拟结果分析

4.1 隧道断面速度分布云图

截取隧道洞内外温差为5℃时，无竖井隧道出口断面速度云图和分布曲线，如图6、7所示。

图6 隧道断面速度分布云图

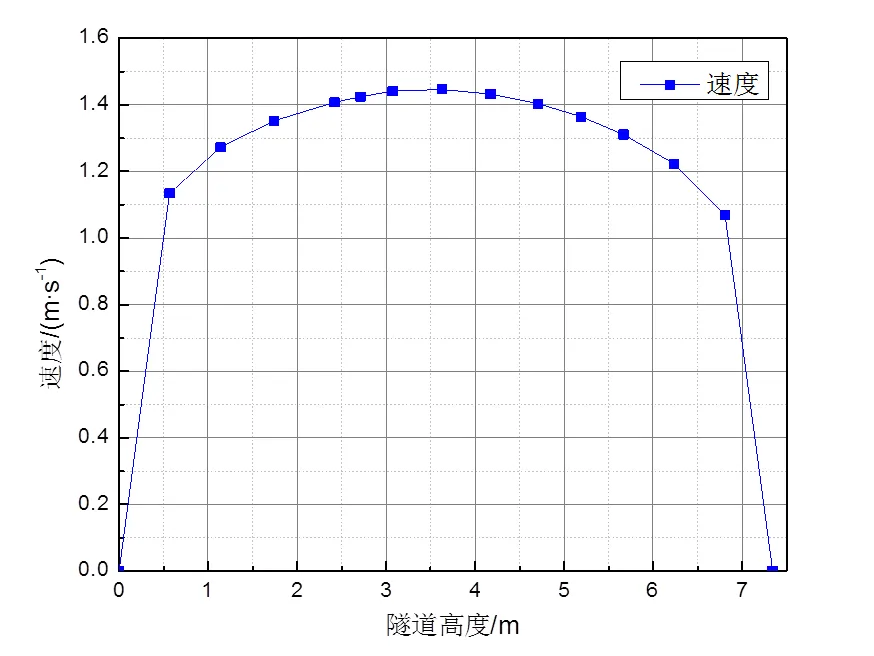
图7 隧道断面速度分布曲线

由图6、7可以看出，隧道断面上速度分布范围较广，呈同心圆状分布，且速度过渡区域范围较小。在靠近隧道壁面区域，速度变化梯度较大，隧道断面中间速度维持在1.1～1.5m/s之间。建议在计算通风换气时长时，选用隧道断面速度平均值。

4.2 竖井位置横向变动

以竖井位置=1500m为例，对单竖井分别布置于隧道正上方和横通道正上方两种工况进行比较分析，隧道纵向速度与压力分布如图8、9所示。

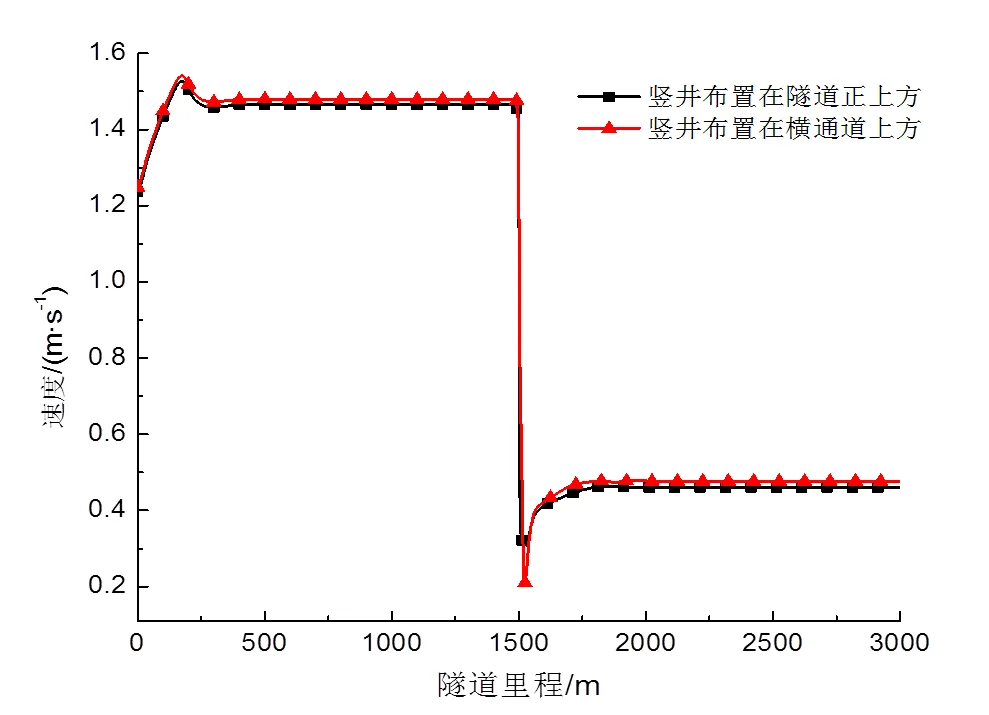
图8 隧道中线速度分布

由图8可以看出，竖井位于隧道正上方时，隧道纵向速度要略小于竖井位于横通道上方时的情形。隧道纵向速度在竖井位置（=1500m）出现断崖式下降，竖井上下游速度落差最大可达1.3m/s，平稳段速度落差也大于1m/s。

由图9可以看出，隧道纵向压力在竖井前后段都呈线性下降，且竖井布置于横通道上方时隧道纵向压力衰减速率要略大于竖井布置于隧道正上方时的衰减速率。隧道纵向压力在竖井位置（=1500m）出现骤降，且竖井布置于横通道上方时压力下降幅值略大。

图9 隧道中线压力分布

由上可知，竖井横向小距离移动对隧道纵向自然通风影响较小，隧道内部局部阻力系数的变化对长大隧道整体通风效果的影响有限。

4.3 竖井位置纵向变动

对竖井位于隧道纵向不同位置时，隧道中线纵向速度、压力分布进行监测分析，如图10、11所示。

图10 隧道中线纵向速度分布

由图10可以看出，随着竖井纵向位置不断后移，竖井位置上下游段隧道纵向速度呈规律性减小（Δ1＞Δ2＞Δ3＞Δ4，Δ′ 1＞Δ′ 2＞Δ′ 3＞Δ′ 4），即竖井位置越靠近入口端，隧道内速度值越大。

由图11可以看出，竖井上游段压力随竖井位置的后移呈线性下降，在竖井底位置压力出现较大的突变，而后竖井压力又随竖井位置后移呈线性下降。且竖井上游段隧道纵向压力衰减速率远大于隧道下游段压力衰减速率，竖井里程较短隧道的纵向压力衰减速率大于竖井里程较长隧道的纵向压力衰减速率，并呈规律性变化。

图11 隧道中线纵向压力分布

在竖井布置于横通道上方，竖井位置沿隧道纵向不同位置布置工况下，将隧道及竖井各出、入口断面的速度平均值作拟合分析，结果如图12所示。

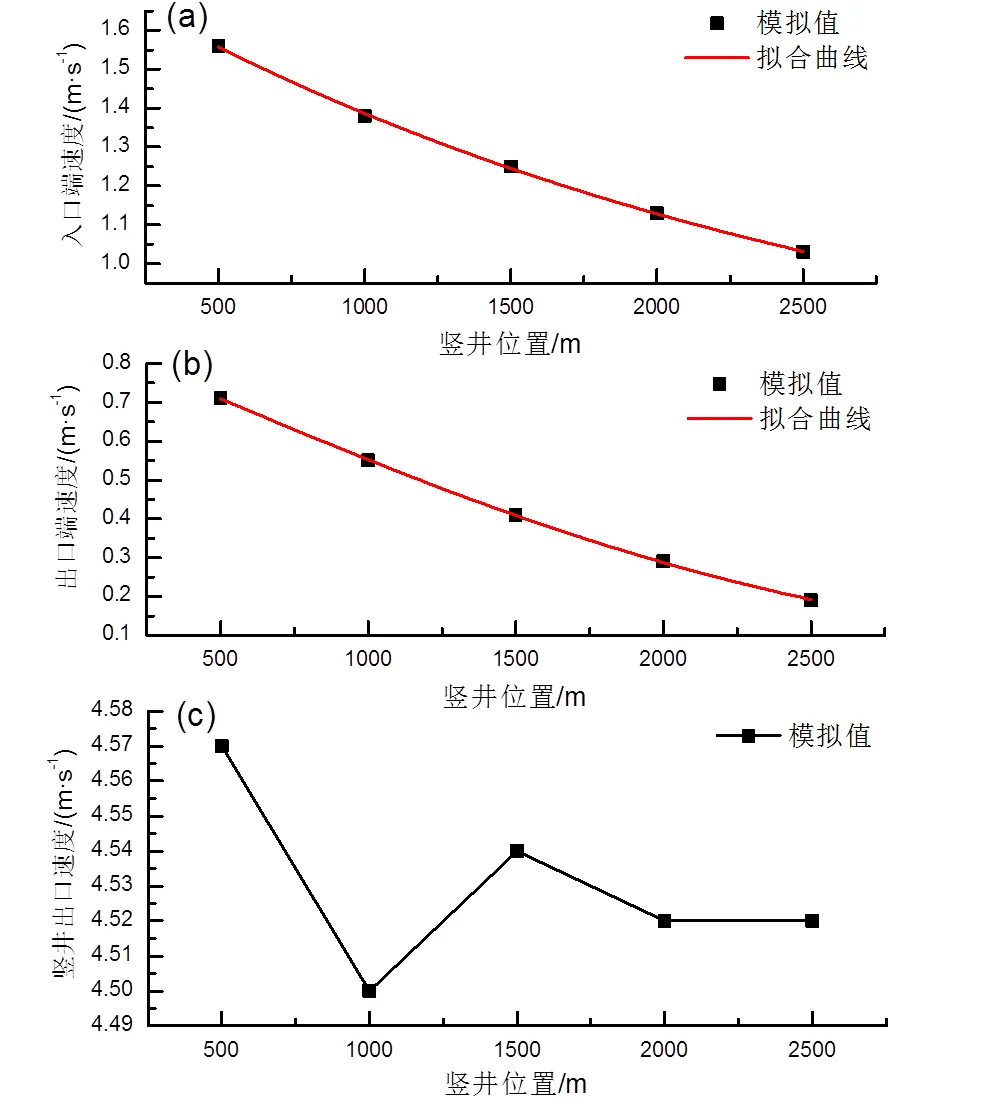
图12 不同断面平均速度与竖井位置的关系

由图12中（a）（b）可以看出，隧道入口和出口端速度与竖井纵向位置呈指数函数衰减，拟合通式为=(2++)，拟合优度大于0.99。由图（c）可以看出，隧道竖井在隧道中部上游移动时，竖井出口速度波动较大，但竖井出口最大速度波动不大于0.07m/s，最大波动率不大于1.6%。隧道竖井在隧道中部下游移动时，竖井出口速度在波动较小，且竖井出口最大速度波动不大于0.02m/s。隧道竖井出口速度受竖井纵向布置位置影响较小。

4.4 隧道通风换气时长

对于单竖井隧道自然通风，对只有一个通风入口情况，隧道通风换气时间可根据下式进行估算：

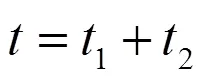
对于隧道两端均为入口，只有竖井一个通风出口的情况，隧道通风换气时间可根据下式进行估算：

通过模拟计算得出隧道在竖井前、后两段区域内的断面速度平均值，通过公式（11）计算得出各段隧道内空气通风换气一次所需要的时间，结果如表3所示。

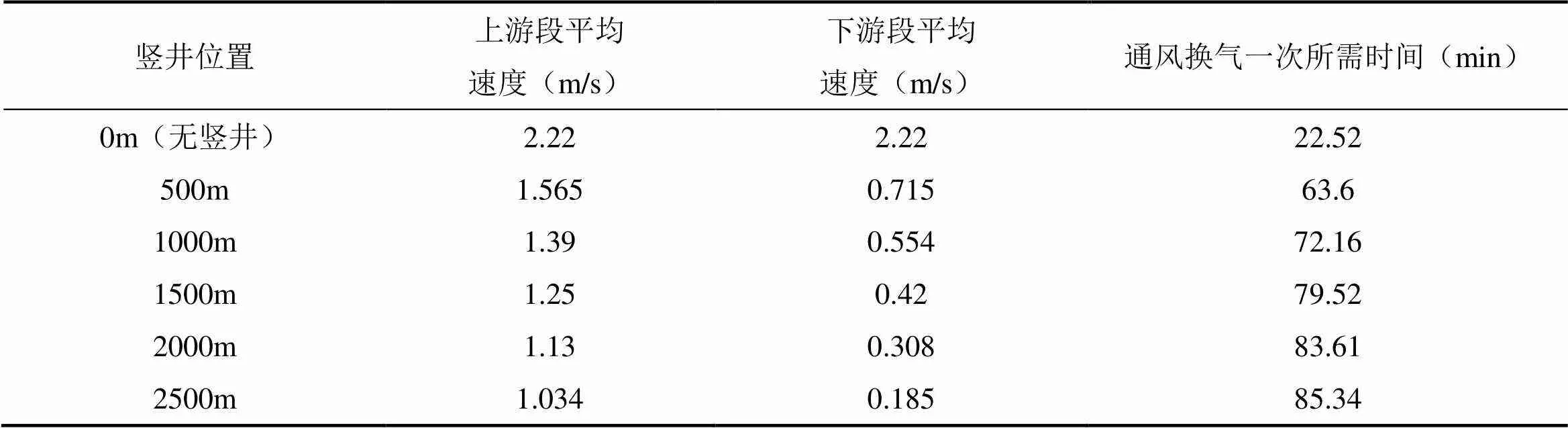
表3 竖井不同位置时隧道通风换气时间

将表3中竖井位置与隧道通风换气时间的关系进行拟合分析，得出一般性规律，如图13所示。

由图13可以看出，竖井位置和隧道通风换气时间呈指数函数递增，拟合通式=(++2)，拟合优度­­2大于0.99。竖井布置位置越靠近来流入口端，对隧道通风时长的影响越大，随着竖井位置的不断后移，其对通风时长的影响逐渐减弱，但所需通风时长总体呈指数增大。

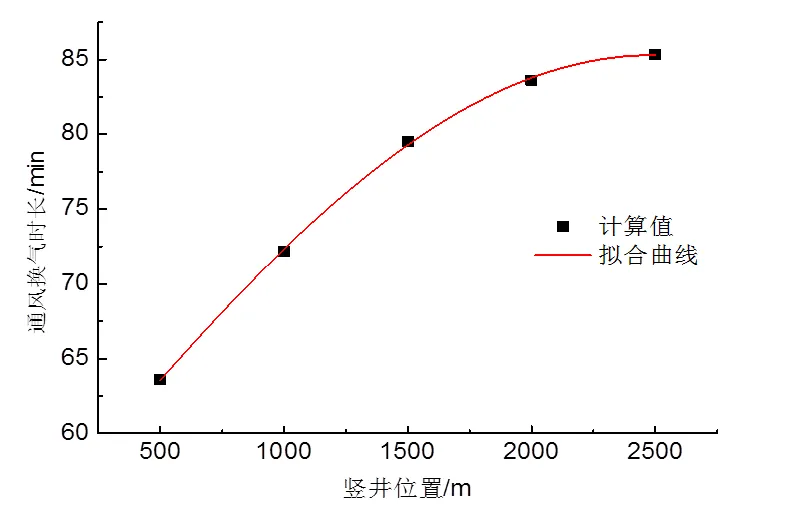
图13 隧道通风换气时长与竖井位置的关系

5 结论

通过对单竖井不同纵向位置下隧道内的通风流场进行模拟，得到隧道、竖井通风换气变化的一般规律。主要结论如下：

（1）对自然通风工况下隧道内风速的确定进行理论分析，运用Fluent软件建立数值模型，其理论计算结果与模拟结果非常接近，验证了模拟方法的可靠性。

（2）竖井横向小距离移动对隧道纵向自然通风影响较小，隧道内部局部阻力系数的变化对长大隧道整体通风效果的影响有限。隧道竖井出口速度受竖井纵向位置影响较小，竖井出口速度的波动极小。

（3）隧道入口和出口端速度与竖井纵向位置呈指数函数衰减。随着竖井位置的不断后移，隧道整体通风换气时间呈指数函数增长。

（4）长大隧道只采用单竖井自然通风时，并不能提升隧道整体自然通风的效果，建议采用竖井通风时要设置其他辅助通风通道或机械通风手段。

[1] 薛运祝.单一竖井对隧道自然通风的影响[J].铁道建筑,1983,(1):18-21.

[2] 朱杰,霍然,孙晓乾.不同竖井侧向开口位置对烟囱效应影响的实验研究[J].工程力学,2008,(9):187-192.

[3] 李志伟,梁习锋,张健.竖井对隧道内瞬变压力的影响[J].中南大学学报(自然科学版),2011,42(8):2514-2519.

[4] 冯炼,刘应清.越江隧道多竖井分段纵向式通风计算方法的研究与应用[J].中国公路学报,2000,(3):63-65.

[5] 杨伟超,彭立敏,施成华.隧道竖井对车体压力的作用机理及影响因素分析[J].中国铁道科学,2009,30(3):68-73.

[6] 王峰,邓园也,王明年.地铁隧道竖井位置优化数值模拟研究[J].计算力学学报,2010,27(3):569-573.

[7] Zhu P G, Tong X N, Chen L, et al. Influence of opening area ratio on natural ventilation in city tunnel under block transportation[J]. Sustainable Cities & Society, 2015,19(2):144-150.

[8] Tamm G, Jaluria Y. Buoyancy and Pressure Driven Flow of Hot Gases in Vertical Shafts with Natural and Forced Ventilation[J]. 2003.

[9] Ji J, Gao Z H, Fan C G, et al. A study of the effect of plug-holing and boundary layer separation on natural ventilation with vertical shaft in urban road tunnel fires[J]. International Journal of Heat & Mass Transfer, 2012,55(21-22):6032-6041.

[10] Li A, Gao X, Ren T. Study on thermal pressure in a sloping underground tunnel under natural ventilation[J]. Energy & Buildings, 2017,147:200-209.

[11] Fan C G, Jin Z F, Zhang J Q, et al. Effects of ambient wind on thermal smoke exhaust from a shaft in tunnels with natural ventilation[J]. Applied Thermal Engineering, 2017,117:254-262.

[12] 金学易,陈文英.隧道通风及空气动力学[M].北京:中国铁道出版社,1983.

Influence of Longitudinal Position of Shaft on Natural Ventilation of Tunnel

Wang Wen1Sun Sanxiang2Chen Junqiang3

( 1.Shaanxi Railway Institute, Weinan, 714000; 2.School of Environmental and Municipal Engineering, Lanzhou Jiaotong University, Lanzhou, 730070; 3.Xinjiang Branch of the First Railway Survey and Design Institute, Urumqi, 830011 )

The role of natural ventilation in tunnel shafts in the operation and ventilation of long tunnels cannot be ignored, so the choice of shaft location is also important. Based on the FLUENT software, the RNG-turbulence model is used to simulate the ventilation results of a single shaft at different longitudinal positions of the tunnel. The wind speed and flow field distribution of the tunnel are obtained when the shaft is located at different positions in the longitudinal direction of the tunnel.Calculate the length of time required for the tunnel to complete a ventilation at the different longitudinal positions of the shaft. The relationship between the position of the shaft and the ventilation time is e-exponential by fitting, which provides a reference for the selection of the location of the shaft and the establishment of ventilation mode in the design and construction of long tunnel.

Natural Ventilation;Shaft;flow field;Numerical Simulation

A

1671-6612（2020）01-070-07

王 文（1990-），男，硕士研究生，助教，E-mail：1205901714@qq.com

孙三祥（1965-），男，教授，E-mail：sunsanxiang@mail.lzjtu.cn

2019-04-02