复合材料球型气瓶的缠绕层设计方法

白文怡 廖英强 张宏亮 刘勇琼

复合材料球型气瓶的缠绕层设计方法

白文怡 廖英强 张宏亮 刘勇琼

（西安航天复合材料研究所，西安 710025）

介绍了一种复合材料球型气瓶的缠绕层设计方法，以某型号球型气瓶为例，分别分析计算了球型气瓶的结构组成、缠绕线型、缠绕角度、缠绕方式和缠绕厚度，为产品后续的仿真与实验提供了必要的理论支持与参考依据，该方法可以推广至后续同类产品。

复合材料；球型气瓶；缠绕层设计

1 引言

高压气体存储的需求随着社会经济的高速发展越来越强烈，气瓶作为一种储气压力容器，被广泛应用于航空、航天、化工、汽车等领域，市场对气瓶需求量也在逐年持续的增长。复合材料气瓶的应用起始于20世纪40年代的美国武器系统，随后的几十年，该项技术逐渐在各国被重视，研究者们以轻质高强为研究目标，开始了针对其材料与结构的不断探索。复合材料缠绕气瓶通常由内层的金属内衬和外层的纤维增强层组成，一般具有以下优点[1]：a.质量轻、刚性好、强度高、寿命长；b.断裂韧性高。增强纤维与树脂基体构成的缠绕层可有效传递载荷，过载时，少量纤维发生断裂，载荷会被重新分配到临近的未发生破坏的纤维上，从而阻止了突发性大面积破坏的产生；c.安全性好。在受到冲击时，损伤破坏表现为基体开裂、纤维断裂分层等形式，但不会产生爆炸碎片，降低了对人员发生伤害的可能；d.耐腐蚀性强。复合材料层由于其自身的特性，不需要经过二次处理即可满足耐腐蚀要求。

球形气瓶的发展起源于某些特定的空间的特殊要求，在一定的使用空间内，其“容积/重量”比相对于其他形式的气瓶更加理想。通过合理的选取缠绕线型，球形气瓶也可以实现近似等强度要求，具有较高的/值[2]。本文总结了一种复合材料球形气瓶缠绕层的设计方法。

2 缠绕层设计方法

2.1 技术指标

某型号球形气瓶主要技术指标如下：形状为两端带有对称极孔球形，容积大于500L，内衬基础壁厚0.8mm，工作压力为10MPa，爆破压力不小于20MPa。

2.2 结构组成

球形气瓶主要结构包括与内部介质接触的金属钛内衬和包裹在金属内衬外的碳纤维缠绕层。其中金属内衬对内起到密封储气的作用，对外则作为缠绕层的缠绕芯模；碳纤维缠绕层由树脂基体和增强碳纤维构成，树脂基体的粘结着增强碳纤维，将载荷分布传递到纤维上，作为整体，该层承担着绝大部分载荷[1]。本文选取TA01钛金属作为内衬，比强度性能优异的T1000GB碳纤维和与碳纤维润湿性良好的BA202环氧树脂体系组成碳纤维增强树脂缠绕层[3]，复合材料性能参数如表1所示[4]。

表1 复合材料性能参数

2.3 缠绕线型

缠绕线型是指在复合材料缠绕气瓶绕制过程中，绕带在芯模上有规律地绕制排布的方式，其中纵向缠绕、环向缠绕、螺旋缠绕是三种基本的缠绕线型[5～7]。在具体缠绕时，单一缠绕线型可能无法满足具体需求，因此可以选择不同的线型进行组合，常用的组合缠绕线型有：螺旋加环向、螺旋加纵向、环向加纵向[4]。球形气瓶可视为两个半球形封头结合在一起形成的气瓶，根据它的形状及结构特点，本文采用螺旋缠绕的方式对其进行缠绕，其经向和纬向强度均由螺旋缠绕纤维提供。

2.4 缠绕角度

图1 纤维在球面上的几何图形

球型气瓶在进行螺旋缠绕时，理论上应该将纤维缠绕在最大直径圆周上，使之不会打滑，在实际缠绕时，利用浸渍纤维的一点摩擦力，使纤维尽量接近大圆即可。如图1所示，缠绕纤维与经向交角在不同纬度上有不同值，在赤道上，交角等于大圆纬度的极角α=90°-，在包络圈纬度上，交角等于90°，在中间任意一点处交角等于[8]：

缠绕角度的计算对后续铺层设计、计算机模拟仿真具有重要意义，是缠绕气瓶设计必不可少的一个环节。

2.5 复合层强度计算与设计

球型气瓶在受内压状态下内衬任意一点的所承受的经纬向薄膜张力分别为为[8]：

式中，1为经向张力；2为纬向张力；为容器内压，为容器半径，r为极孔（或扩孔）半径，为球面任意一点的纬度圆半径。

球面上的薄膜张力如图2所示。

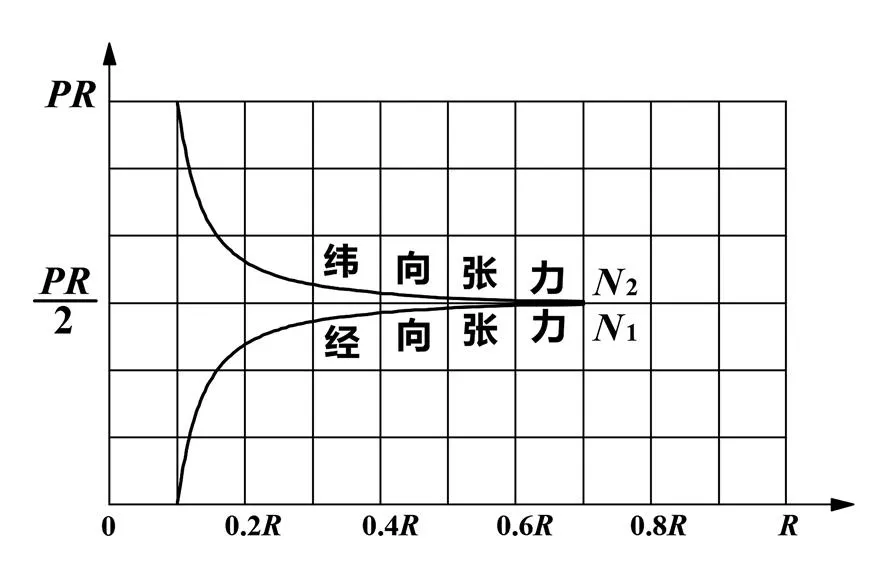
图2 两极开孔球壳在内压下所受薄膜张力

缠绕层任意一点的所承提供的经纬向抗力为[8]：

式中，1为经向抗力；2为纬向张力；单位宽度上纤维股数，n为赤道上纤维股数，为每股纤维的抗力。

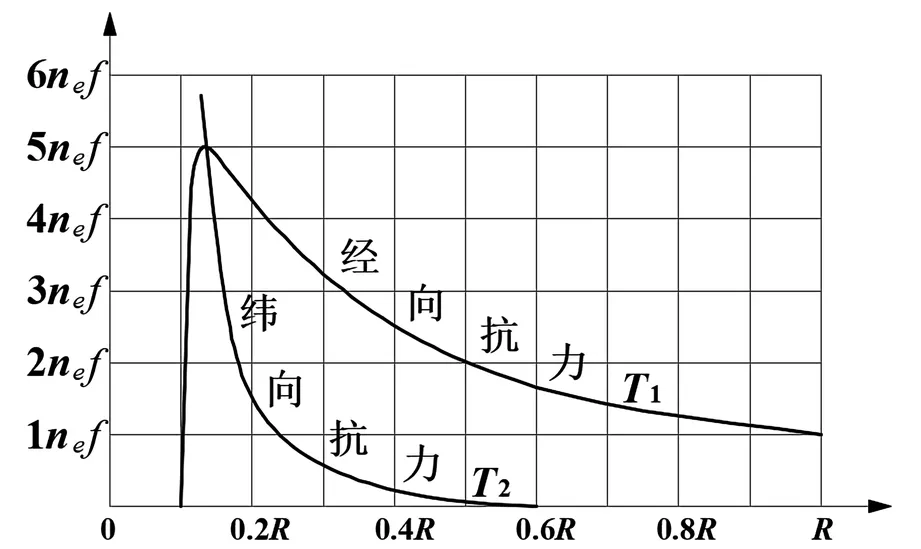
图3 缠绕纤维在球壳表面上的纤维抗力

球面上的纤维抗力如图3所示。由图3可以看出，=0.1时，经向抗力为0，纬向抗力最大，且纬向抗力随着半径增大下降地非常迅速，在赤道处几乎为0；经向抗力一开始迅速增大，然后又缓缓下降，在赤道处最小。结合图1可知，如果只缠绕一个包络圈来满足球壳承受的压力，在绝大部分区域内，纤维纬向抗力决定着纤维缠绕量，这种缠绕方式会造成纤维大量冗余，为充分利用纤维抗力，需要采取多包络圈的缠绕方法。在具体缠绕过程中，先在极孔纬度处，绕制一定数量的纤维以满足极孔附近的强度要求，再扩大包络圈直径，缠绕一定数量的纤维该纬度处的强度要求，再扩大包络圈直径，再缠绕……直到满足容器的强度要求即可。

根据技术指标要求，该球型气瓶缠绕层设计有19个包络圈，且各包络圈位置如表2所示。

表2 球型气瓶包络圈设计结果

根据已设计的缠绕工艺，对气瓶各位置经纬向张力、抗力计算结果如图4、图5所示。

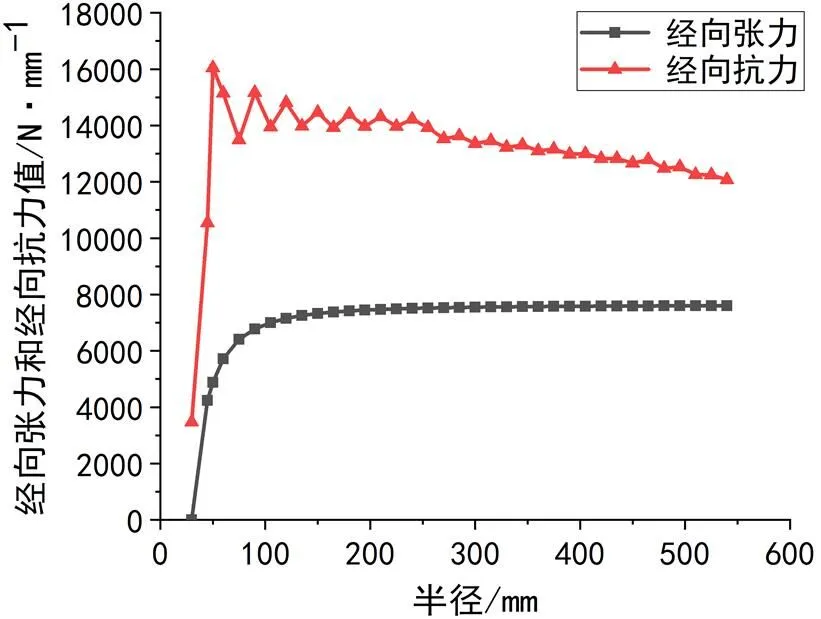
图4 不同半径位置处经向张力和经向抗力的对比图

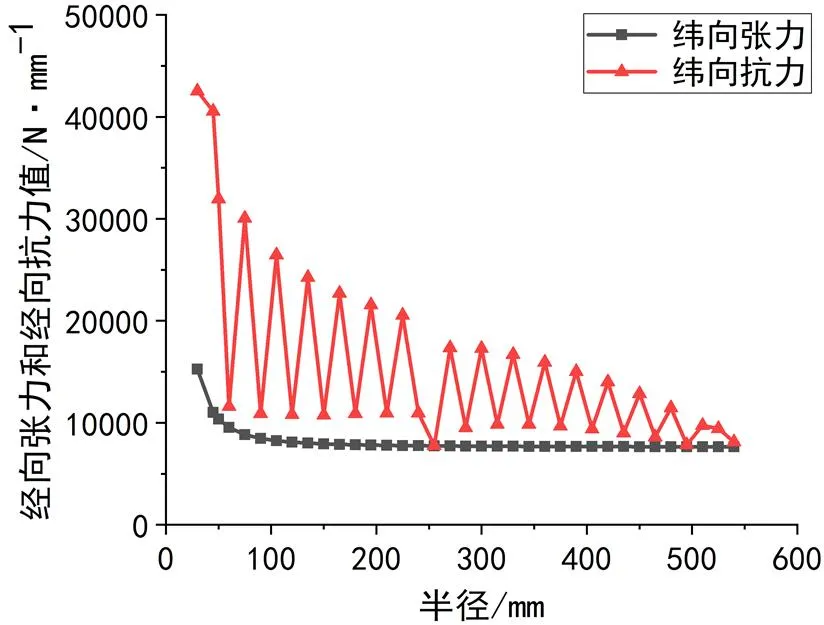
图5 不同半径位置处纬向张力和纬向抗力的对比图

从图中可以看出：该工艺设计方案下，气瓶的经向抗力要高于经向张力，纬向抗力高于纬向张力，因此产品的经向、纬向强度能够满足要求，且在图中容易看出，在半径255mm，465mm和540mm处，纬向抗力与张力十分接近，在爆破实验中，地方将会首先发生失效。

2.6 缠绕厚度

在纤维缠绕球形气瓶设计中，气瓶整体的应力，转动惯量，气口接头高度，爆破压力的预测等都有赖于缠绕层厚度的计算，因而准确确定缠绕层厚度就变得十分重要，气瓶厚度计算需分为两个部分。

一个带宽范围外的缠绕层厚度计算方法：

一般情况下，对于任一角度的缠绕层，普遍采用以下公式来计算[9]：

式中，0为赤道处缠绕角度，为封头计算位置缠绕角度，t0为纱带厚度或纤维单层厚度。

将每个包络圈一个带宽范围外的厚度线型叠加之后，所得厚度如图6所示。

图6 一个带宽范围外纤维缠绕总厚度

一个带宽范围内的缠绕层厚度计算方法：

在极孔或包络圈附近时，→90°，t=∞，这说明在极孔或包络圈上纤维堆积的非常剧烈，而实际上，由于纤维束总有一定宽度，不会集中在一处，所以我们经常用Kurt通用双公式法[10]或补充双公式法[9]来计算距离极孔或包络圈一个带宽范围以内的纤维堆积厚度：

Kurt通用双公式：

补充双公式：

式中，为带宽，为带距。

如图7所示，针对本文中的球型气瓶，使用两种方法计算而来的包络圈附近的堆积厚度差别很小，本文选取计算数值相对较大的补充双公示法以增加气瓶的可靠性。

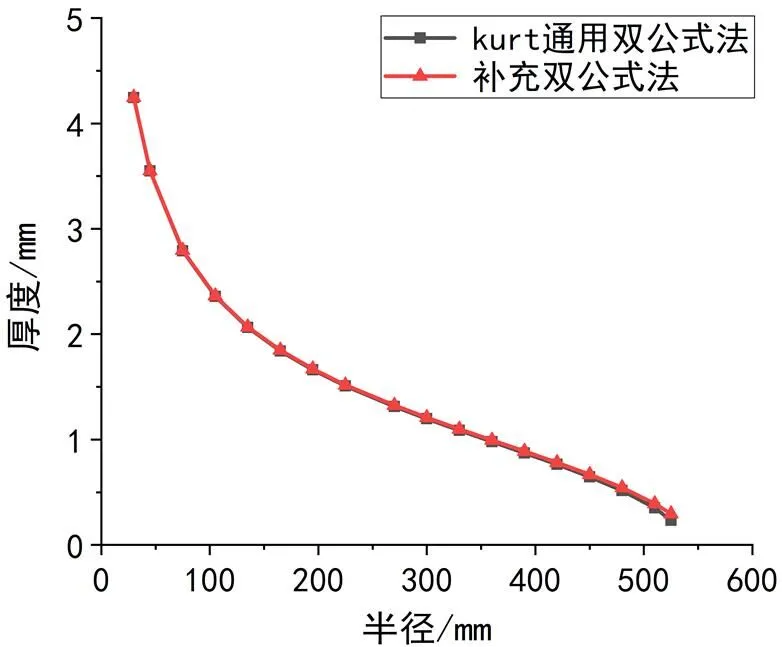
图7 两种不同算法一个带宽范围内纤维缠绕厚度对比图

以上计算均为干纤维厚度，在考虑BA202树脂基体后，纤维缠绕层整体总厚度变化如图8所示。

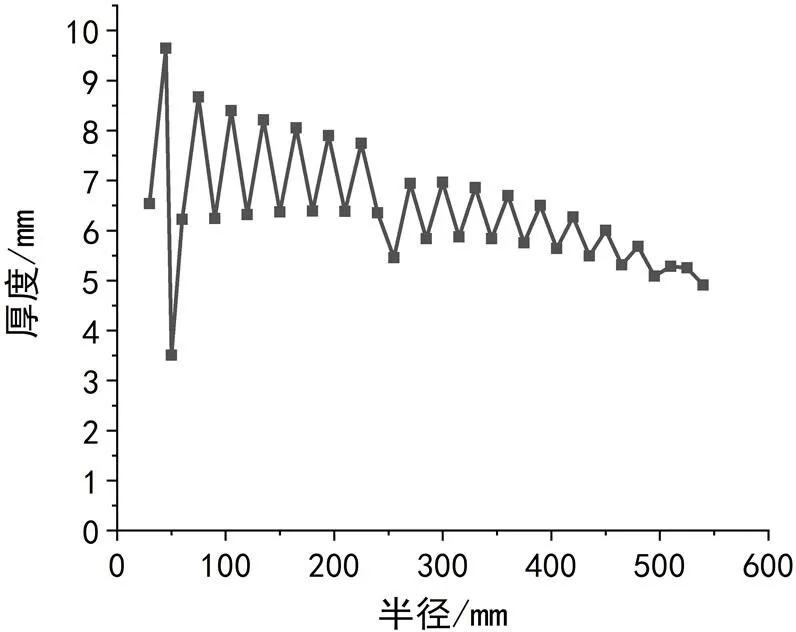
图8 球型气瓶纤维缠绕层总厚度

由图8可以看出，纤维缠绕球型气瓶最厚处在第二包络圈半径以外一个带宽范围内，最大厚度9.6mm，最薄处在第二包络圈以内，最小厚度3.5mm，距离赤道越近，缠绕层厚度越小，并逐渐收敛于3.9mm，气瓶球形曲面并不圆滑，存在多圈微突起同心环形结构，这是由于球形气瓶缠绕依据等强度设计理论，为使结构充分受力，同时最大限度减小结构层重量，采用扩孔缠绕工艺必然产生的包络圈所致。为保证球形瓶表面整体圆滑，后续还需要在包络圈外表面增加修饰层。

3 结束语

针对具体算例，详细阐述了碳纤维复合材料球形气瓶缠绕层设计方法，对缠绕层各项参数进行了介绍与设计计算，并得出相关结论，总结如下：

a. 球形气瓶可视为由两个封头组合而成的气瓶，螺旋缠绕是球形气瓶常采用的一种实用且高效的缠绕方法，气瓶经纬向抗力均由螺旋纤维提供。

b. 由于球型气瓶自身固有的特性，一般采用多包络圈设计法，按这种方法设计出来的球型气瓶可形成一个近似等强度结构，多包络圈设计法大大减少了球型气瓶的纬向抗力冗余，对气瓶减重有着重要意义，且通过计算制图，可以较为明显地发现气瓶薄弱点，预测失效位置。

c. 不同位置，球型气瓶的缠绕厚度计算方法也不同，在计算极孔或包络圈附近纤维堆积厚度时，Kurt通用双公式法和补充双公式法差距很小，可以任意选取。此外，通过计算球形气瓶不同位置的缠绕厚度，可以预测其表观圆滑程度。

d. 本文所介绍的设计方法不仅对球型气瓶缠绕层进行了设计，还对后续计算机仿真具有指导与对照作用。

1 徐君臣，银建中. 纤维缠绕复合材料气瓶研究进展[J]. 应用科技，2012(4)：64～71

2 姜广祥. 纤维缠绕球形压力容器的结构与性能[J].纤维复合材料1989 (3)：22～26

3 王晓洁，梁国正，李辅安，等. T-1000碳纤维/环氧树脂基复合材料性能研究[J]. 材料科学与工艺，2005，13(5)：540～543

4 李玉峰，靳庆臣，刘志栋. 复合材料高压气瓶的碳纤维缠绕设计和ANSYS分析技术[J]. 推进技术，2013(34)：968～976

5 刘雄亚，谢怀勤. 复合材料工艺及设备[M]. 武汉：武汉理工大学出版社，1997

6 贾晓龙，李刚，薛忠民，等. 碳纤维/环氧树脂在橡胶内衬表面的全缠绕工艺设计[J]. 玻璃钢/复合材料，2009(2)：6164

7 陈祥宝. 树脂基复合材料制造技术[M]. 北京：化学工业出版社，2000

8 上海玻璃钢研究所. 玻璃钢结构设计[M]. 北京：中国建筑工业出版社，1980

9 陈林泉，王路仙. 纤维缠绕壳体封头厚度计算[J]. 推进技术，1995(6)：36～40

10 Kurt C G. 纤维缠绕压力容器的圆顶厚度[J]. 外国导弹与航天运载器，1991(3)：66～75

Winding Layer Design Method of Composite Spherical Cylinder

Bai Wenyi Liao Yingqiang Zhang Hongliang Liu Yongqiong

(Xi’an Aerospace Composites Research Institute, Xi’an 710025)

This paper summarizes a winding layer design method for composite spherical cylinder. Taking a certain type of spherical cylinder as an example, analyzes and calculates the structural composition, winding line shape, winding angle, winding method and winding thickness of the spherical cylinder. This method provides a necessary theoretical support and reference for subsequent simulation and experiment of the product, and the method can be extended to subsequent similar products.

composite；spherical cylinder；winding layer design

白文怡（1992），在读硕士，材料科学与工程专业；研究方向：复合材料力学。

2019-12-19