挡板鼓泡床内气泡特性的CFD模拟分析
石孝刚, 赵国静,2, 吴迎亚, 王溢萍, 高金森, 蓝兴英
(1.中国石油大学(北京) 重质油国家重点实验室,北京 102249;2.北京辰安科技股份有限公司,北京 100094)
气-固鼓泡流化床具有良好的混合、传热及传质效果,在过程工业中有着广泛的应用[1],其中催化裂化装置中的汽提器是鼓泡流化床的典型工业应用[2]。在催化裂化汽提器中,蒸汽和催化剂颗粒逆向接触汽提出油气,气-固接触效率对汽提效率有着显著的影响。气-固鼓泡床中不可避免地存在着气泡,而大尺寸气泡会导致固体颗粒返混严重、气-固接触不均匀[3-4],减小气泡大小可以改善床内流化状态,有效地强化传质和传热[5-6]。目前,可采用设置内构件和电磁场等手段来破碎气泡,强化传质、传热作用。其中,添加内构件是较为经济简捷的手段,在工业上应用广泛。
为了提高催化裂化装置的汽提效率,国内外研究者一直致力于改进和优化汽提器内构件的研究[7-17]。这些研究的大部分是采用冷态实验来考察内构件的宏观作用,受实验检测方法的限制,难以对床层内部的微观流动状况,如气泡大小、形状、频率等特性进行测量,因此需要借助计算流体力学(CFD)方法对气-固鼓泡床内构件的作用机制进行深入研究。目前,CFD方法已成功实现了对鼓泡床中气-固两相流动行为的模拟研究[18-24],笔者所在课题组基于CFD模拟结果建立了气泡特性的分析方法[25],剖析了自由鼓泡床内气泡大小、形状、速率的整体分布特性以及气泡的生命周期。
鼓泡床内添加内构件后气-固流动情况将发生变化,特别是其中的气泡运动状态将大大不同于自由鼓泡床。笔者基于挡板鼓泡床实验装置的数据,采用CFD方法对其内部的气-固两相流动进行模拟研究,并与无挡板的自由鼓泡床进行对比,分析有、无挡板的鼓泡床中气泡运动特性的差异,揭示挡板对鼓泡床内气泡的作用机制。
1 数学模型
采用欧拉-欧拉双流体方法(TFM)结合颗粒动理学理论(KTGF)对鼓泡床内气-固流动两相流动进行模拟计算。双流体模型将气-固相当作连续介质,气-固两相均满足质量、动量和能量守恒方程。颗粒相压力、黏度、剪应力、剪切黏度等性质采用颗粒动理学理论来表征。气-固相间作用力通过曳力模型来描述,曳力模型是模拟成败的关键。对于Geldart A类颗粒的气-固鼓泡床,在流动过程中由于颗粒间存在较强的黏附力,使得颗粒容易发生团聚,使得气-固相间作用力降低。Gidaspow[26]、Wen-Yu model[27]、Ergun model[28]以及Turton model[29]等经典曳力模型均高估了床层的膨胀率。为此,研究者们采用了各种方法对曳力模型进行修正[18-24,30-31]。笔者所在课题组采用颗粒团聚物直径来修正曳力模型,通过实验测得的颗粒终端速率计算颗粒团聚直径,在颗粒和颗粒聚团2个尺度对曳力进行模型化,成功模拟了Geldart A类颗粒鼓泡床内气-固流动[21-22,32]。因此,本研究中将采用该曳力模型对挡板鼓泡床内气-固流动进行模拟计算,关于流体模型的详细描述及相关表达式见文献[21-22]。
2 模拟对象
模拟对象为文献[4,33]中的一套挡板流化床冷模实验装置。流化床主体部分尺寸为0.5 m(长)×0.03 m(厚)×6 m(高)。在距床层底部0.8 m处安装了一层挡板,其主要结构参数:挡板垂直高度h为0.07 m、挡板片间距d为0.04 m、挡板水平方向倾斜角度θ为55°。挡板的结构示意图如图1所示。
实验所用的颗粒为FCC催化剂,颗粒密度为1500 kg/m3,堆积密度为922 kg/m3,颗粒平均粒径为64 μm。实验所用的气体为空气,其密度为1.225 kg/m3,黏度为1.7×10-5kg/(m·s)。床层内颗粒藏量约为18 kg,初始床层高度为1.28 m,操作气速为0.02~0.20 m/s。
在挡板鼓泡床的模拟计算中,计算时间步长为0.001 s,气体流经整个床层所需要的时间约为7 s,为了得到更稳定的床层,共模拟流动时间为40 s,在后续分析床层及气泡特性时,选取20~40 s之间的数据进行分析。

图1 挡板结构示意图Fig.1 Structure of the baffles
3 气泡分析方法
为了研究挡板鼓泡床的气泡特性,基于模拟计算得到的鼓泡床内固含率分布图建立识别和分析气泡的方法[25],如图2所示;采用图像处理软件ImageJ对气泡特性,如中心坐标、气泡数量、气泡面积、气泡尺寸等进行计算,并采用Matlab软件对数据进行批处理[25]。具体步骤如下:(1)将如图2(a)所示的固含率分布图选择一个合适的固含率阈值识别和提取气泡(一般定义鼓泡床中固含率小于0.2的区域为气泡);(2)根据所选定的阈值将模拟得到的鼓泡床内固含率分布图二值化(将图像上像素点的灰度值设置为0或255),见图2(b);(3)通过边缘检测算法,确定气泡的边缘,见图2(c);(4)计算气泡的位置和面积;(5)对相邻帧的气泡进行对比分析,求取气泡运动速率。此外,为了进一步表征气泡的特征,对气泡进行球形近似,通过气泡当量直径表征气泡的大小。

图2 鼓泡床气泡分析方法Fig.2 Method of bubble characterization(a) Solid volume fraction; (b) Binarization figure;(c) Bubbles distribution
4 结果与讨论
4.1 网格无关性及模型验证
根据上述挡板流化床冷模实验装置,建立模拟对象的二维几何结构,其尺寸为0.5 m(长)×6 m(高)。为了确定模拟结果与网格尺寸的无关性,笔者利用软件ICEM-CFD对上述二维几何结构进行网格划分,分别构建了3种不同尺寸的结构化网格,网格尺寸分别为15.0 mm、7.5 mm和2.5 mm。网格示意图以7.5 mm网格为例,如图3所示。采用ANSYS Fluent对气相和固相的流动进行了模拟计算。表1为采用不同网格模拟得到的床层膨胀高度与实验值对比。挡板鼓泡床的初始床层高度为1.28 m,表1中数据显示,通入气体后床层发生膨胀而变高,网格尺寸为15.0 mm时所预测的床层膨胀高度和床层膨胀比均比实验值高;而网格尺寸为7.5 mm和2.5 mm所预测的床层膨胀高度和床层膨胀比与实验值基本接近,由此可见,采用7.5 mm和2.5 mm 2种网格均能较好地模拟出挡板鼓泡床的膨胀特性。较细的2.5 mm网格所需要的计算时间长,增加计算成本。综合模拟结果准确性和计算成本,笔者选取7.5 mm的网格进行模拟研究。

图3 网格尺寸为7.5 mm的网格示意图Fig.3 Grid with a mesh size of 7.5 mm

表1 不同尺寸的网格预测的床层膨胀高度与实验值对比Table 1 Bed expansion height and bed expansion ratio inbaffled fluidized bed with different mesh resolutions
文献中常采用Darton等[34]和Werther[35]经验关联式来预测鼓泡床内气泡当量直径(De),其表达式分别见式(1)和式(2)。笔者将模拟计算得到的气泡当量直径与这2个经验关联式计算值进行对比,如图4所示。由图4可知,沿着床层高度方向,气泡当量直径逐渐增大;在低气速下(0.026 m/s)模拟值与经验关联式计算值吻合得很好,在较高气速下(0.186 m/s)吻合程度略变差。总体而言模拟值与经验关联式计算值的偏差均在20%以内,说明笔者所建立的气泡分析方法具有较好的适用性。
Darton et al.经验关联式:
(1)
Werther经验关联式:
De=d0[1+27(u0-umf)]1/3(1+6.4H)1.21
(2)
其中,A0为气体分布器气体入口面积,m2;De为气泡当量直径,mm;d0为常数,d0=0.00620 m;g为重力加速度,m/s2;H为床层高度,m;u0为表观气速,m/s,在本研究中u0为0.02~0.20 m/s;umf为初始流化速度,m/s,对于FCC颗粒,umf=0.025 m/s。
4.2 气泡特征
鼓泡床添加内构件后其中的气泡运动状态将大大不同于自由鼓泡床,为了揭示挡板对鼓泡床内气泡的作用机制,采用前述的气泡分析方法对挡板鼓泡床内的气泡进行分析,并与无挡板的自由鼓泡床进行对比,分析有、无挡板的鼓泡床中气泡特性的差异,见图5和图6。从图5可以看出,在挡板鼓泡床中,从底部均匀进入的气体部分发生聚集形成气泡,气泡经过挡板时受挡板作用,大气泡破碎成小气泡,当气泡离开挡板一定距离后,小气泡又重新聚并为大的气泡。与之对比,在图6所示的无挡板自由鼓泡床的相同区域内并未发生显著的气泡破碎过程,整体上沿着床层高度气泡尺寸不断变大。为了更直观地观察挡板对气泡的影响,笔者追踪图5(a)中挡板下方的一个大气泡经过挡板时尺寸变化过程。该气泡(方框所圈起的气泡)在挡板下方时气泡当量直径为59 mm,在挡板上方区域气泡当量直径减小为33 mm(图5(e))。而图6(a)中2个气泡(方框所圈起的气泡)当量直径为56 mm;当气泡运动到图6(f)位置时气泡当量直径变成170 mm;沿床层高度气泡不断变大。可见,挡板在一定区域内增强了气泡的破碎,减小了气泡的尺寸。挡板的存在对气泡形态也产生了影响,观察图5中气泡形态可知,在挡板作用区域内气泡倾斜且呈现细长形状,气泡的倾斜角度和尺寸与挡板结构相关。与之对比,在图6所示的无挡板自由鼓泡床内,气泡主要以近似椭圆的形状存在。
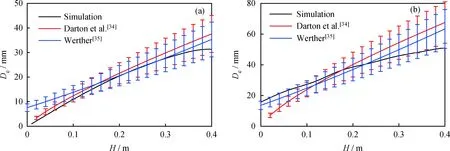
图4 气泡当量直径(De)模拟值与经验关联式对比Fig.4 Comparison of bubble equivalent diameters (De) between simulation and empirical correlations(a) ug=0.026 m/s; (b) ug=0.186 m/sug—Gas velocity; H—Bed height

图5 挡板鼓泡床内气泡运动状态Fig.5 Baffled fluidized bed flow characteristicst/s: (a) 31.15; (b) 31.25; (c) 31.40; (d) 31.45; (e) 31.60; (f) 31.70
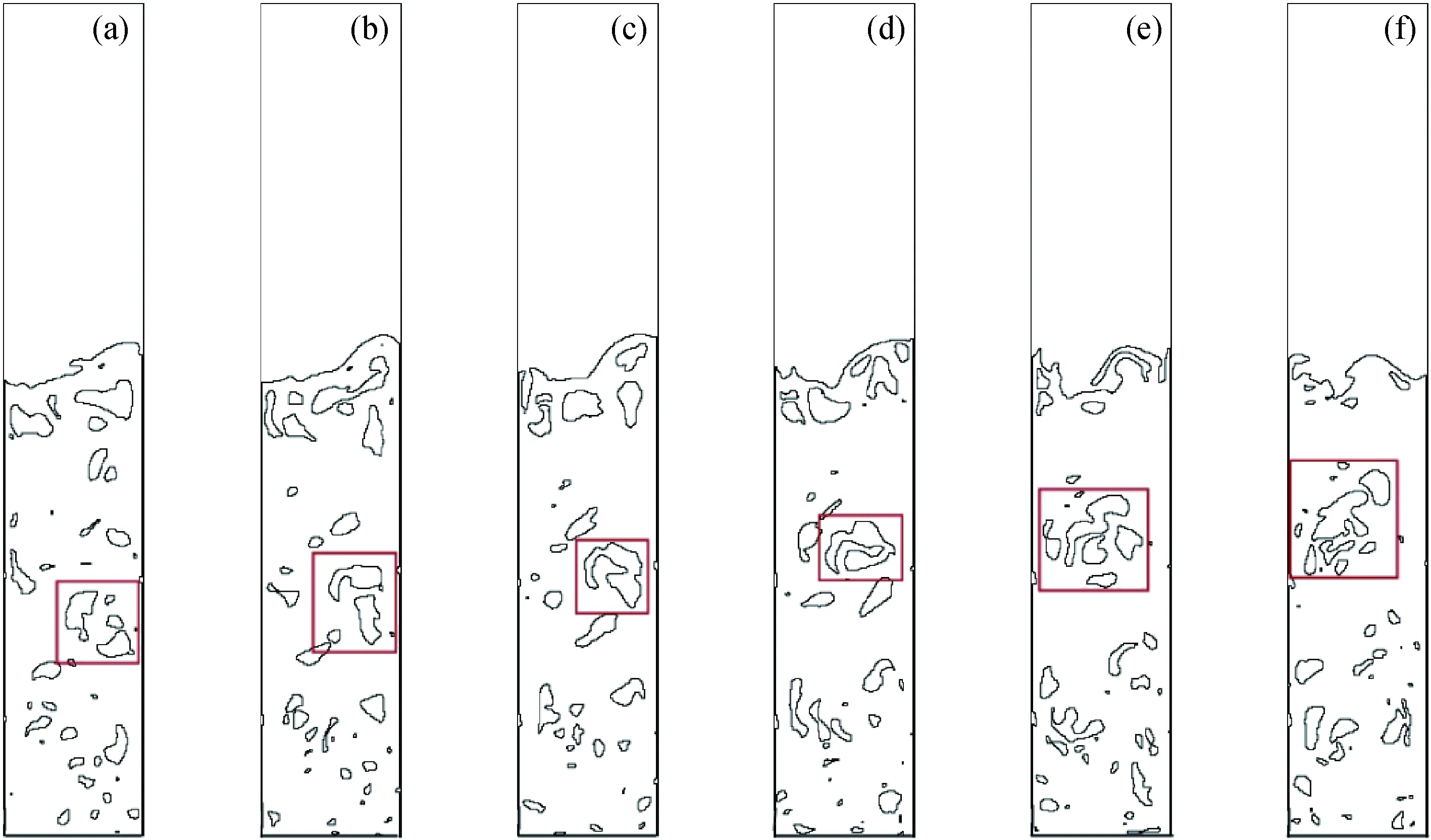
图6 自由鼓泡床内气泡运动状态Fig.6 Baffle-free fluidized bed flow characteristicst/s: (a) 31.54; (b) 31.64; (c) 31.70; (d) 31.78; (e) 31.80; (f) 31.98
为了进一步考察单层挡板对整个床层气泡行为的影响,对有、无挡板的鼓泡床内沿床层高度的气泡当量直径和上升速率进行了统计,所得结果如图7 所示。从图7(a)可以看出,在挡板鼓泡床底部无挡板区域,气泡尺寸变化规律与无挡板自由鼓泡床相似,均呈现先增加后趋于稳定的趋势;而在挡板及附近区域内,气泡被挡板破碎成小气泡,气泡尺寸减小;在挡板上方一定区域,小气泡又重新聚并,气泡尺寸又逐渐增大。对床层内所有气泡尺寸进行统计发现,挡板鼓泡床内床层气泡平均尺寸比无挡板鼓泡床小。经统计,挡板鼓泡床内气泡当量直径为40 mm,每一时刻平均气泡数目为63个;无挡板鼓泡床内气泡当量直径为44 mm,平均气泡数目为48个,定量说明了挡板在破碎气泡方面的优良性能。
由图7(b)可以看出,在挡板床下部,气泡上升速率沿着床层高度增加,在接近挡板处,气泡速率急剧减小,使得气体在挡板下方聚集形成“气垫”区域,离开挡板一定距离后,气泡速率沿着床层高度又继续增加,到达一定高度之后气泡速率维持在一个范围内。与之对比,在无挡板的自由鼓泡床内,沿着床层高度方向气泡速率先逐渐增加,到达一定高度后气泡速率就维持在一个范围内。由图7还可以发现,挡板对气泡尺寸和上升速率的影响被限定在一定范围内,说明挡板只在有限区域内起作用(本研究中,该区域为挡板以下0.2 m,挡板以上 0.4 m 的区域),如果需要在整个床层内控制气泡行为,应设置多层挡板。
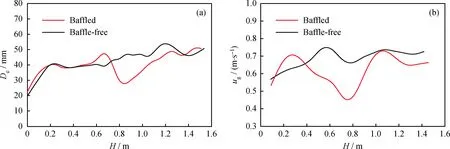
图7 有、无挡板鼓泡床内不同床层高度上气泡当量直径(De)和气泡上升速率(ug)的变化Fig.7 Axial distribution of bubble equivalent diameter (De) and bubble velocity (ug) in baffled or baffle-free fluidized bed(a) De; (b) ug
4.3 操作气速对气泡的影响
操作气速对鼓泡床内气泡行为有着显著影响,是实际工业生产中十分重要的操作和调节参数。为此,在上述研究基础上进一步对操作气速对鼓泡床内气泡行为的影响进行模拟分析。图8和图9分别为不同气速下挡板鼓泡床和无挡板鼓泡床内固含率和气泡分布。可以看出,随着操作气速的增加,有、无挡板的鼓泡床内均呈现出气泡尺寸变大,气泡数目增多以及床层膨胀高度增加的趋势。但是,与无挡板鼓泡床相比,在相同的较高气速下,挡板鼓泡床内的气泡数目更多,尺寸更小,床层膨胀高度也更大,床层整体更为疏松,气、固接触更加均匀。

图9 不同气速(ug)下无挡板鼓泡床内固含率和气泡分布图Fig.9 Solids volume fraction and bubbles at different gas velocities (ug) in baffle-free fluidized bed(a), (c), (e), (g): Solids volume fraction; (b), (d), (f), (h): Bubble distributionug/(m·s-1): (a), (b) 0.05; (c), (d) 0.10; (e), (f) 0.15; (g), (h) 0.20
图10为不同气速下有、无挡板鼓泡床内平均气泡当量直径和气泡数目的分布情况。由图10可以看出,随着气速的增加,有、无挡板的鼓泡床中平均气泡当量直径不断变大,气泡数目不断增加。在相同气速下,挡板鼓泡床平均气泡当量直径小于无挡板鼓泡床,挡板鼓泡床气泡数目多于无挡板鼓泡床,气速越大,气泡数目的差别越明显。其原因为,在无挡板鼓泡床中,气泡生长所受约束较少,随着气速增加,气泡不断变大;而在挡板鼓泡床中,挡板不仅抑制了气泡的生长,而且还将大气泡破碎成小气泡,气速提高后所生成的大气泡都在挡板的作用下破碎成小气泡,使得气泡数量明显增多。对比不同气速下有、无挡板鼓泡床内平均气泡当量直径和气泡数目可以发现,在较低气速下挡板对鼓泡床内气泡的影响较小,随着气速的增加,挡板对气泡的作用逐渐加强。

图10 不同气速(ug)下有、无挡板鼓泡床内平均气泡当量直径(De)与气泡数目Fig.10 Mean bubble equivalent diameter (De) and bubble number at different gasvelocities (ug) in the baffled and baffle-free fluidized bed(a) De; (b) Bubble number
5 结 论
采用欧拉双流体方法结合颗粒动理学理论对挡板鼓泡床内气-固流动进行模拟计算,基于模拟结果建立了识别和分析挡板鼓泡床内气泡特性的方法,应用该方法对挡板鼓泡床实验装置进行模拟分析,并与无挡板的自由鼓泡床进行对比,分析有、无挡板的鼓泡床中气泡运动特性的差异,揭示挡板对鼓泡床内气泡的作用机制,得到了以下结论:
(1)在挡板鼓泡床中,从底部进入的气体部分发生聚集形成气泡,气泡经过挡板时受挡板作用,大气泡破碎成小气泡,当气泡离开挡板一定距离后,小气泡又重新聚并为大的气泡。
(2)挡板鼓泡床内气泡当量直径小于无挡板鼓泡床,而挡板鼓泡床内气泡数目多于无挡板鼓泡床。挡板只在一定区域内对气泡存在作用,如需在整个床层内调控气泡行为,需要设置多层挡板。
(3)随着操作气速的提高,有、无挡板的鼓泡床内均呈现出气泡尺寸变大、气泡数目增多、床层膨胀高度增加的趋势。
(4)操作气速越大,有、无挡板的鼓泡床内气泡数目的差别越明显。在较低气速下,挡板对鼓泡床内气泡的影响较小,随着气速的提高,挡板对气泡的作用逐渐加强,使得气、固接触更加均匀。

