油库控制系统改造中关键点的设计研究
李野
(中国航发沈阳发动机研 究所科研保障部,辽宁 沈阳 110015)
1 引言
试验基地的供油控制系统,担负着发动机试验过程的供油任务。运行过程中,控制系统要对供油压力进行连续的采样监控,反馈的压力经过PID 运算后,输出信号到泵组,由此保持油压的恒定。为了提高动力供应质量、保障设备可靠运行,系统采取了如的冗余措施:三点压力反馈和双泵组备份,以保证试验过程的连续性。
冗余技术是保证系统安全和可靠运行的主要手段,通常是采用多模冗余的方式。目前,常用的冗余结构主要有双机热备份结构、二乘二取二结构和三取二结构等。IEC61508-1997 推荐了5 种安全系统的结构,并计算了各种结构的可靠性,三取二结构是其中可靠性最高的一种。因此,实际控制系统中的油压反馈采用了三点方式,通过软件进行三取二表决,以实现抛弃异常数据及故障,而且不影响系统正常运行的功能。
三取二是一种三模冗余结构,它的关键是:表决器的设计以及表决器如何通过特定算法来实现。本文试图对泛泛的烦琐理论描述如何能够转化并应用于实际进行探讨。由于表决器的算法受到数据的实时同步、运算量和运算速度等因素制约,如何提出简洁实用的算法是本文关心和讨论的焦点,对不同算法的安全性和可靠性仅做简单评估。
2 三取二表决的实现方法
三取二的关键是如何进行表决,其实现方法有两种:采用针对系统设计专用附加模块(通过CPU 或FPGA 模块)实现;利用系统自身的CPU 计算功能实现。对于实时性要求不严格的大多数控制系统而言,如果能够设计一个简单合理的算法,系统中的处理器完全有能力来完成表决功能,相比较采用附加模块而言,这种方式更加经济、可靠和灵活。针对此方法进行讨论如下:
2.1 三取二表决结构模型
三取二的表决可将其视为一个软件系统模块(以下简称表决模块),它通常嵌入整个软件系统中。表决模块的输出是对输入信号进行少数服从多数的表决结果,表决是多模冗余安全系统中最主要的功能。
三取二表决结构根据不同的应用要求,可分为多环节表决或单环节表决。多环节表决的结果其可靠性更高,但对于算法设计、硬件和运算速度的要求也高,这种适合安全和稳定性要求极高的场合,它可以大幅度提高系统的整体可靠性;反之,单一环节的表决结果可靠性相对较低,但可以满足安全性和稳定性一般的场合。
三取二表决结构模型如图1 所示。
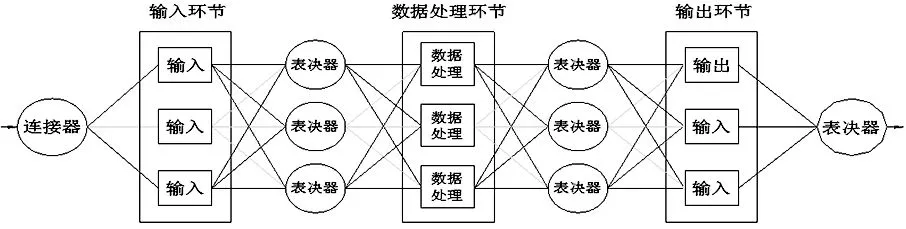
图1 三取二表决结构模型
图1 是一个多环节分布式三取二表决结构,在多个环节进行多点三取二表决。
2.2 三取二表决的数学表达及模型选择
三取二理论简单描述是:当且仅当两个以上的模块同时出现故障时(发生概率较低)才输出错误结果。这种描述似乎使得多数人在逻辑上发生混乱,背离了“三取二”字面的上的含义(有一个不正确的时候取两个正确的输出)。三取二表决可用如下三个数学表达来描述:

这三个表达式代表了三种三取二表决模型的布尔代数(Boolean algebra)方程。它们均可完成三取二表决。其中A、B 和C 代表三个输入变量的状态,Y 为输出结果;虽然三种不同的三取二表决完成了相同的功能,但是,使用马尔可夫建模分析其安全性和可靠性时,所得到的状态转移图(马尔可夫连)不同,最终获得的可靠性和安全性的结果是不一样的。同时,它们运算的复杂程度也不同。
参考使用马尔可夫模型对系统建模仿真分析的结果,综合考虑它们的可靠性和安全性评估结果后,最优的选择应该使用表达式(2)对应的模型2;其次,是表达式(1)对应的模型1;最后是表达式(3)对应的模型3。
模型1 于模型2 的差别是:模型1 的安全性在理论100小时前差一些,但此后会表现出与模型2 相同的可靠性。考虑到模型1 的表达式中均为相同的逻辑“与”运算项,便于编程设计和模块化处理。因此,实际使用中采用模型1 完成三取二表决,完成压力信号的处理和故障判断。
2.3 可行性论证
2.3.1 表达式的适应性分析
三取二表决的实现,是建立在布尔状态下的。换句话说,它们是基于数字电路来完成的,其电路原型如图2 所示,图2 是表达式①的电路。
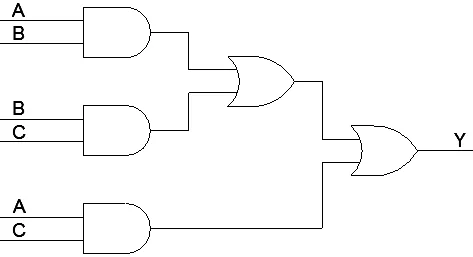
图2
参考表达式(1)以及电路原型可以看出:三个输入变量状态仅有真(True=1)和假(False=0)两个状态。当其中一个变量的输入状态出现错误时,假设变量C 的状态为false,表达式中仅A·B 项结果为真(True 或1),另外两个分项(B·C)和(A·C)均为假(false 或0)。就是说,表达式(1)的结果Y 是取用了A 和B 两项输出,抛弃了C 项。从电路中也可看出,Y 输出采用了A 和B,完成了三取二的功能,这正是我们所期望结果。试想,如果我们不使用电路而是采用软件方式来实现,即在软件中分别执行表达式(1)中的三个分项的“与”运算,根据运算结果同样可判断各个输入变量的真和假的状态。
2.3.2 输入变量状态转换的提出
将表达式(1)应用于实际时会遇到一个限制且需要解决的问题是:当输入变量为模拟量时(而且我们的实际系统就是模拟量的压力反馈值),表决模块无法判断该值的真假(或者说对与否),因为模拟量不是二态的变量,无法应用于布尔代数的运算。为了实现对模拟量进行三取二表决,就要将模拟量 形式的输入变量转换为布尔量,然后,才能根据表达式(1)中的描述,分三次对三个变量分别做布尔“与”运算,得到对应的运算结果;最后根据运算结果,判定并抛弃失效数据。
本文现提出“互为参考标准模式”的方法,将布尔的“与”运算过程,换为数据的减法运算,间接地将输入变量为模拟量状态转换为布尔状态,同时完成等效的布尔“与”运算结果,最终实现三取二表决的运算。公式如下。

上述公式中,引入了K 判定因子,数据的绝对值与判定因子K 的运算结果,即代表各分项的布尔“与”运算结果。因子K 可以在前也可以在后,视编程方便确定。
当运算结果大于0 时,判定为真(True);当运算结果小于0 时,判定为假(False)。
若判定因子K 置于绝对值运算后,则做如下更改:当运算结果小于0 时,判定为真(True);当运算结果大于0 时,判定为假(False)。
运算输出结果S1、S2和S3分别代表了公式(1)中的A·B、B·C 和A·C 的布尔状态。
上面结果成立的条件是:三个 反馈单元的动态响应速度在规定的范围内(远小于采样周期);三个参数必须为同步数据(同一时刻测采样值);两个以上的反馈单元不会在同一时刻均出现故障。
2.3.3 算法分析和验证
依据公式(4),若A-B 的绝对值小于K 值时,S1(Status1)的结果大于0,S1为真。说明A 变量和B 变量的差在允许的范围内,可判定A 和B 正常;反之,当它们的差值超过K 规定值时,S1(Status1)的结果小于0,S1为假,可判定A 或B 的数据有一个异常。当S1为假时,继续判断S2,若S2为真,说明A 变量的数据不能采用;同样,依据公式(5)和(6)可以确认状态S2和S3的真和假。3 个状态仅有如下组合:
(1)全部为真:3 个数据均可信,反馈单元(变送器)均为正常;
(2)仅其中一个为真:对应的两个数据可信,另外一个反馈单元数据不可信;
(3)全部为假:有2 个数据以上不可信,需报警处理。
2.3.4 数据的采用
当S1、S2和S3全部为真时,表决系统可取三个数据的平均值输出;
当S1为真时,表决系统应取A 和B 两个数据的平均值输出。C 为故障;
当S2为真时,表决系统应取B 和C 两个数据的平均值输出。A 为故障;
当S3为真时,镖局系统应取A 和C 两个数据的平均值输出。B 为故障。
2.4 算法限制
2.4.1 使用考虑因素
使用本文提出的算法时,需要考虑如下问题:数据的同步;数据异常的判断标准;数据过程状态(动态过程还是稳态过程)。这三个因素是完成准确判断的必要条件。
数据同步:三个数据必须是同一时刻的数据。
数据异常的标准:取决于K 值的选用。
数据过程状态:动态过程还是稳态过程。当三个数据严格同步时,适合动态状态下的表决判定。反之,应予以考虑。
2.4.2 判定因子的取值考虑
判定因子K 值的大小,决定了数据不一致的严格性。应考虑实际中反馈源的误差、现场的干扰等不确定因素。
K 值过小,容易造成误报警;反之,K 值过大,会导致报警失败。
K 值选择应当遵循“故障—安全”的原则。
2.4.3 安全性考虑因素
针对输入的初态和动态过程,其安全性有待商榷。
算法的安全性和可靠性目前尚未进行分析,但可以使用状态转移图做评估。
2.4.4 判定逻辑的优化
在“算法分析和验证”以及“数据的采用”章节中,简单描述了数据真和假的判断以及如何采用数据。实际使用时,应当穷尽所有分项的状态判断,组织严格的逻辑以减少误判的可能并保证数据输出的正确性。对非法逻辑出现的响应,应采取相关措施来保证系统的安全性和可靠性。判定逻辑的优化在此不再描述。
3 实现与结果分析
根据本算法实施的模拟量三取二表决和故障判断模块,已用于试验基地供油控制系统的软件中。控制系统使用新的控制软件已正常运行至今,并且成功判定出反馈器件的故障并做出正确报警指示,系统抛弃了故障器件的数据继续平稳运行,没有导致压力的波动或停机事件发生。根据事后的实际检测,报警指示的反馈器件确有问题,目前尚未发生误报记录。从实际结果可以证明这种表决算法可行。
4 结语
本文提出的模拟量三取二表决算法,简洁实用、便于普通编程者理解和编程;因运算简单且运算量及小,不会占用控制系统中CPU 的大量时间;方便程序的移植和修改。
本方法的提出仅当抛砖引玉,相信有很多同行有更简洁和巧妙的思路,实现并完成模拟量形式的三取二表决算法,欢迎探讨和指教!

