基于自适应算法的IPMSM无速度传感器研究

涂 炜，江卫华，胡为兵，崔耕韬

（武汉工程大学 电气信息学院，武汉430205）

内置式永磁同步电动机（IPMSM）以其体积小、效率高、控制性能好、功率密度大等优点被广泛应用于电动汽车、工业控制、高性能交流调速领域。 在高性能电动汽车控制领域中，整车系统控制的可靠性尤为重要，当电动汽车运行在较差的工况时会导致速度传感器出现故障，使整个控制系统的可靠性变低，也会导致对电机的维护人员带来了一定的困扰，速度传感器会增加电机的体积并且会导致电机成本较高。 为了解决针对传统机械式传感器带来的不便和困扰，许多国内外学者开始进行无速度传感器的研究并取得了很多成果。

1 控制策略的改进

目前，永磁同步电机的无速度传感器方案有高频注入法、扩展卡尔曼观测法、滑模观测器法、模型参考自适应法等[1-3]。 文献[4]使用高频注入法，需要注入脉振高频电压信号，通过一定带宽的滤波器后可得到转子位置信息， 但仅适合零速或低速控制，而且在中高转速不适用于简化模型。 文献[5]使用滑模观测器法，滑模观测器法主要利用开关函数作为控制系统的运动状态，使其在滑模面上运动的状态最终达到稳定，该方法对外部具有一定的抗干扰性和对电机参数变化不敏感性，但该方法的开关函数和滤波器会给系统以及电机带来延迟，增加电机的抖动。 文献[6]使用扩展卡尔曼观测法，不需要电机的具体参数， 而且能有效地减少干扰和噪声影响，但其建模比较繁琐，分析参数比较困难。

模型参考自适应算法是一种适合中高速控制的较为简单的控制策略。 它简单易于实现而且能保证参数估计的渐进收敛性，但是对电机参数依赖要求较高并且抗干扰能力弱。 可以利用滑模变结构控制抗干扰能力和对参数不敏感的特点，与模型参考自适应相结合，取代传统模型参考自适应中PI控制器， 从而设计出变结构模型参考自适应控制器，可以增强系统的稳定性能和抗干扰能力。 在此采用内置式永磁同步电机在恒转矩区进行对2 种控制策略稳定性分析和验证，在MatLab/Smulink中搭建了仿真模型，试验证明在负载干扰下和转速突变情况下，新型的控制策略较传统模型参考自适应的估算精度较高，系统的抗干扰性能和鲁棒性较强。

2 IPMSM 的数学模型

三相永磁同步电机具有复杂电磁关系、各分量耦合以及系统非线性等特点，为了简化模型，对永磁同步电机做以下基本假设[7-10]：

1）定子电枢绕组中会产生正弦感应电动势，转子永磁体的气隙磁场也呈正弦分布在气隙空间中；

2）定子和转子铁芯的涡流和磁滞损耗可以忽略不计；

3）电机输入为对称三相电流，不含高次谐波；

4）定子铁芯的饱和可忽略，d 轴和q 轴电感为常数，磁路为线性。

基于上述假设，便于解耦控制，可将三相静止坐标系变换为两相旋转坐标系。

IPMSM 定子电压方程为

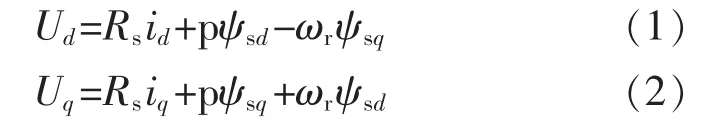
磁链方程为

电磁转矩方程为

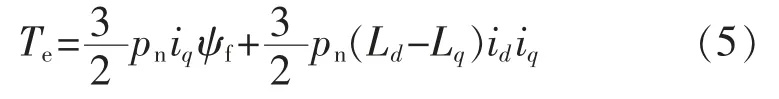
式中：Ud，Uq为定子d，q 轴等效电压；Ld，Lq为定子d，q 轴等效电感；ψsd，ψsq为定子d，q 轴等效磁链；ψf为永磁体磁链；ωr为电角速度；p 为微分算子；pn为极对数；Te为电磁转矩。

3 传统模型参考自适应基本原理

通常，传统模型参考自适应系统MRAS 估算的方法，是将不含真实转速的磁链方程（电压模型）作为参考模型，而将含有待辨识转速的磁链方程（电流模型）作为可调模型[11]。其主要原理是将含有估计量的可调模型与含有真实观测量的参考模型作一个偏差，而该偏差信号传递给适应机构，利用适应机构中的比例积分控制器运算后，产生自适应控制信号作用于可调模型中，最后使2 个模型的误差趋近于一定范围内，以实现控制对象的输出量跟随参考模型的输出量。 模型参考自适应系统的基本结构如图1 所示。

图1 模型参考自适系统的基本结构Fig.1 MRAS system basic structure

3.1 MRAS 数学模型

内置式永磁同步电机在d，q 轴旋转坐标系下定子电流方程为

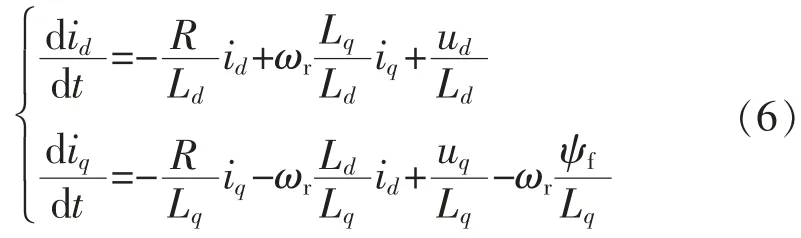
将该方程变换为矩阵形式，即

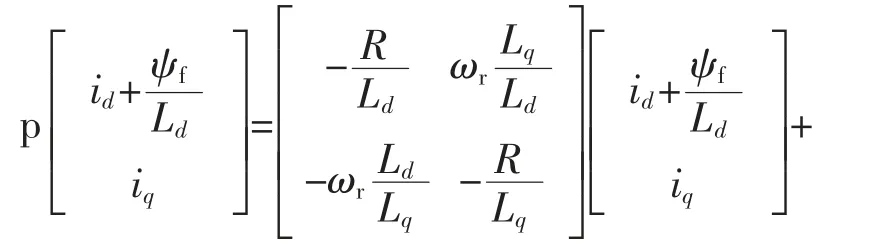
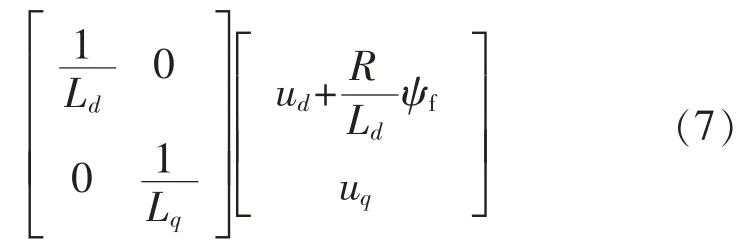
可得

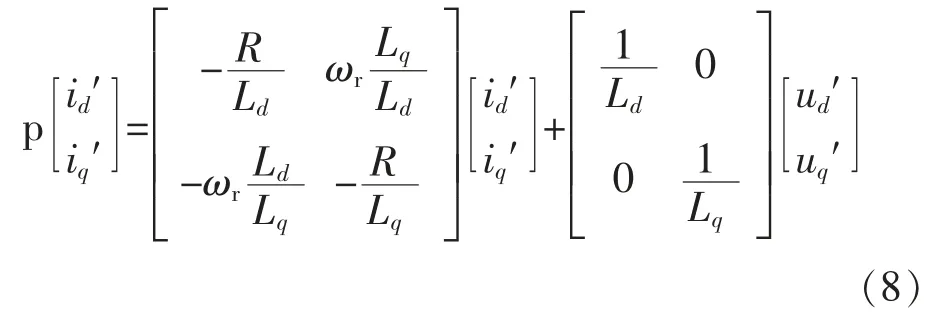
其中定义

式（8）可以改写为状态方程形式，即

用估计值表示式（8），可得

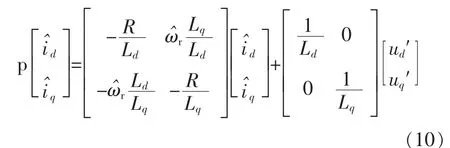
进一步将式（10）改写为状态方程式，即

将式（8）中旋转d，q 轴等效电流、电压和转子转速视为电机自身已知的真实参数时，则可以视为参考模型。将式（10）中含有观测的电流和待估算的电角速度，则可以视为可调模型。

3.2 自适应律的建立

模型参考自适应算法中， 为使系统趋于稳定，应选择合适的自适应律，而自适应律的建立有多种方法，在此选用波波夫（Popov）超稳定性理论性设计分析。

定义广义误差为

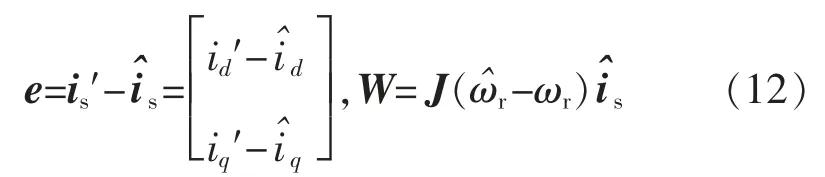
将式（9）参考模型减去式（11）可调模型，可得

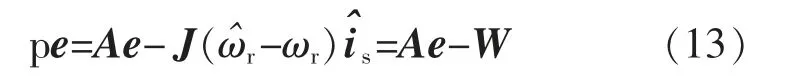
其中

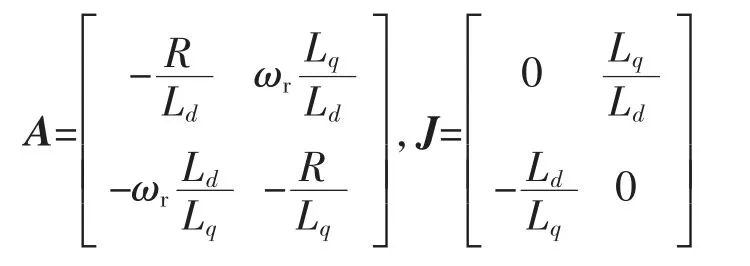
由式（13）可以构建如图2 所示标准的非线性时变反馈系统，V=De。 为计算简单，可以使矩阵D 为单位矩阵I，即图中上部分为线性时不变环节，r=0，u=-W，而W 由V 通过非线性环节得到。

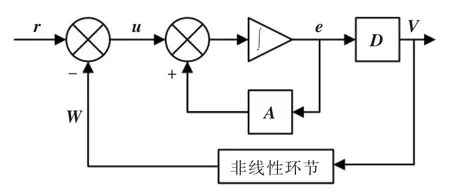
图2 非线性时变反馈系统Fig.2 Non-linear time-varying feedback system

根据Popov 超稳定理论可知， 要使模型参考自适应系统趋于稳定，上述非线性时变反馈系统应满足以下2 个条件：

1）线性时不变环节的传递函数矩阵必须是严格正实的，即G（s）=D（sI-A）-1需要保证正实性；

2）对于非线性时变环节，则必须满足Popov 积分不等式：

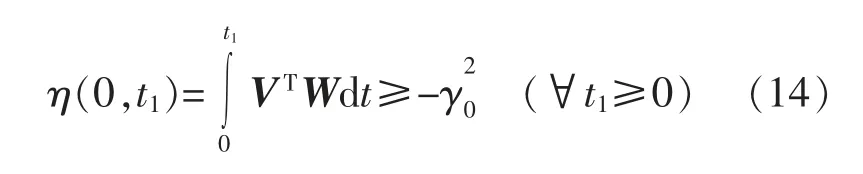
通过计算很容易验证线性时不变环节的传递函数矩阵是正实的，而为了得到模考模型自适应中待估算转速的自适应规律就得逆向求解Popov 积分不等式，将W 和V 的表达式代入式（14），可得

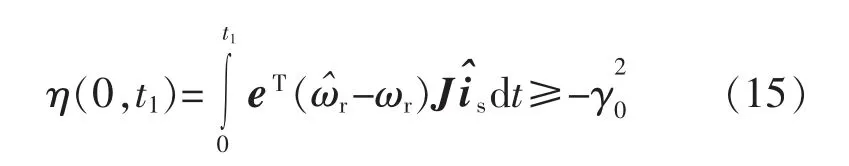
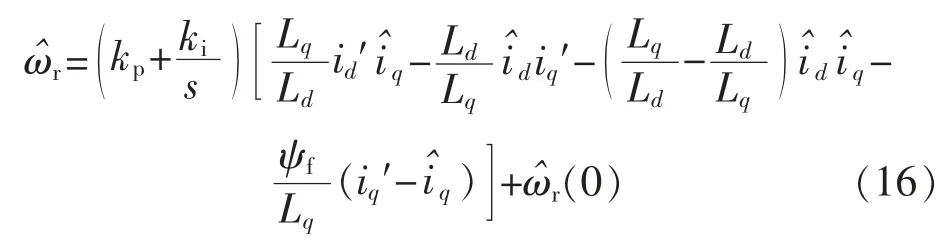
4 滑模变结构的基本理论

滑模变结构控制是根据输入状态达到切换函数要求时，改变反馈量u（x）的极性及大小，使控制器从一种结构切换到另一种结构，以满足系统所需要控制性能[12-13]。 变结构函数一般形式为

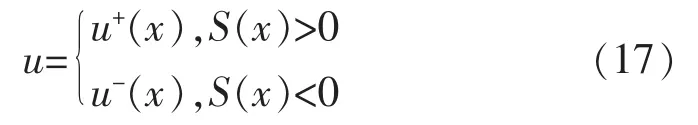
其中

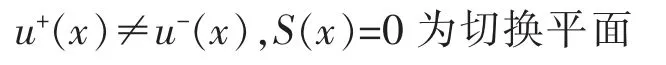
其切换原则是保证最终滑动模态的稳定性和品质。

以参考模型和可调模型的实际电流和估计电流的差值e 选取变结构的滑模面s=S（e），从而替代MRAS 中固定PI 参数控制器，则可以建立变结构模型参考自适应中的滑模面函数方程为

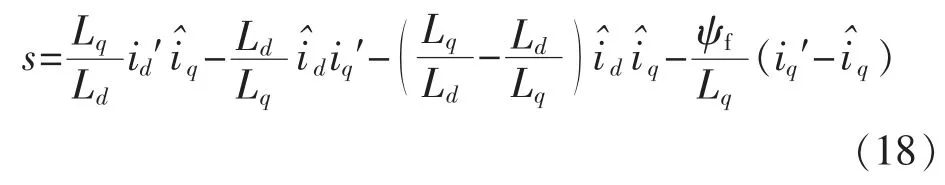
在此选取的是常值滑模变结构开关增益u0，由于传统的滑模变结构控制采用符号开关函数（sign），会给系统带来抖动和不稳定性。 为增强系统的稳定性，设计了一种软开关函数Sigmoid，根据系统要求可以推出切换控制函数u=u0Sigmoid（s），而软开关函数为

式中：a>0，其大小会影响系统的收敛性，应选择合适大小的值。

滑模面和常值控制率的确定，可以推出滑模变结构MRAS 的速度观测表达式，即

式中：u0为滑模增益。而为了使滑模变结构MRAS 运行稳定，利用Lyapunov 稳定性定理分析：

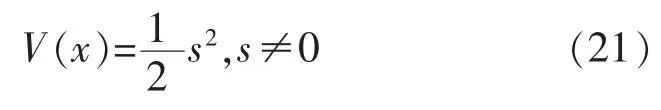
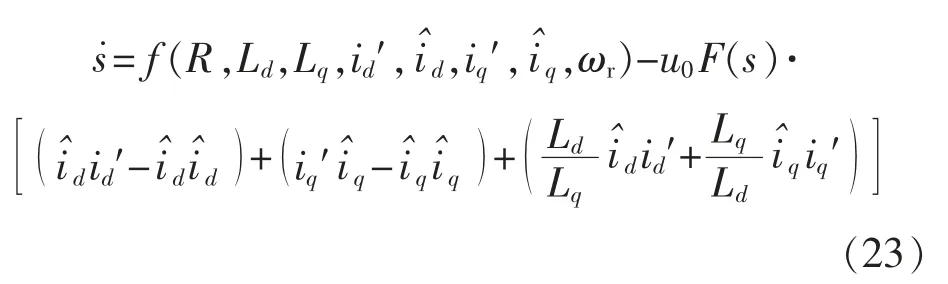
5 仿真分析

为验证内置永磁同步电机在传统模型参考自适应（MRAS）和新型滑模变结构MRAS 两种控制策略的性能对比， 将采用MtLab/Simulink 中对图3 所示的采用变结构模型参考自适应算法的IPMSM 无传感器FOC 控制原理框图进行建模仿真试验。主体部分为逆变器、变结构MRAS 模块、SVPWM 模块和比例积分控制器等，其中用变结构模型参考自适应算法替代了传统的速度测量传感器。 电机仿真参数见表1。

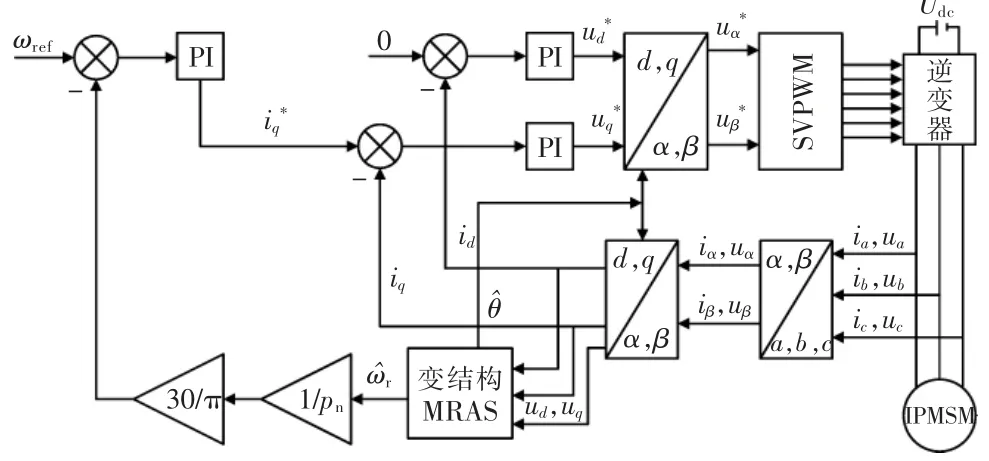
图3 变结构模型参考自适应IPMSM 无传感器矢量控制框图Fig.3 SM-MRAS IPMSM speed sensorless vector control block diagram

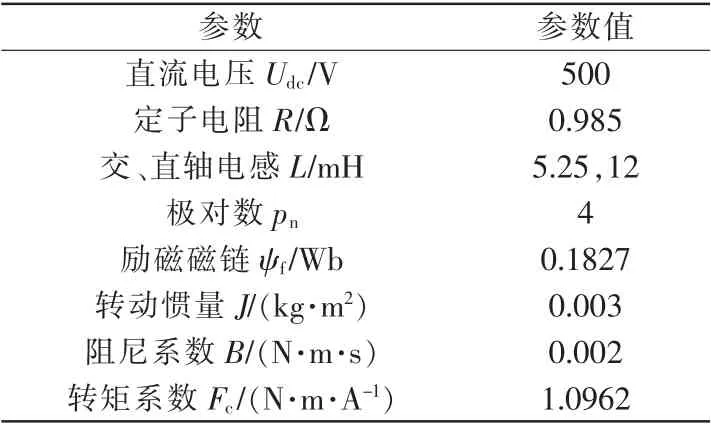
表1 内置式永磁同步电机仿真参数Tab.1 Simulation parameters of IPMSM

电流环和速度环中PI 调节器的设计是根据工程经验计算确定大致范围， 再根据具体仿真波形加以调整，最终确定电流环的比例系数为18，积分系数为5220，而速度环的比例系数为0.08，积分系数为4.2；变结构中α 为1.1，滑模变结构增益u0为440。

试验1 电机以2 N·m 带的负载启动运行，给定速度为阶跃信号起始500 r/min 到0.25 s 突变为800 r/min。 传统的MRAS 和变结构MRAS 转速突变速度曲线如图4 所示。 由图可见，传统的MRAS和变结构MRAS 都能较好地跟随实际转速，但是传统的MRAS 电机在启动估算值和实际值的波动较大。

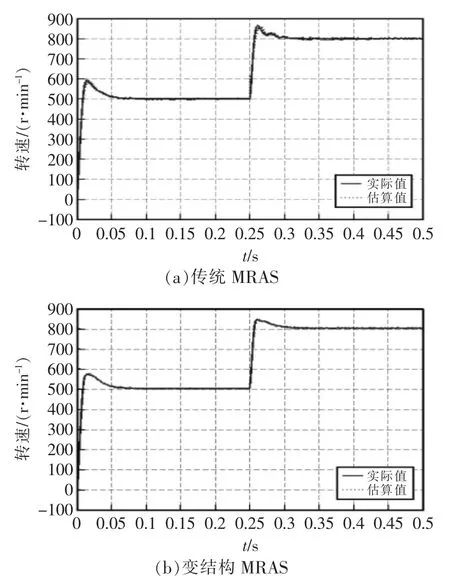
图4 两种MRAS 转速突变速度曲线Fig.4 Abrupt speed curves of two kinds of MRAS rotation speed

传统的MRAS 和变结构MRAS 转速突变误差曲线如图5 所示。 由误差曲线可见，启动转速误差达到±20 r/min，此时估算的转速有小幅度震荡，而变结构MRAS 启动估算的转速和实际转速误差很小，可以看出启动时的估算转速有±4 r/min 的误差； 而在0.25 s 时转速突变，传统的MRAS 误差高达120 r/min，而变结构MRAS 只有25 r/min 的误差，且从该转速突变点后变结构MRAS 转速曲线较为平滑，即可证明变结构MRAS 的抗干扰能力更强，估算精度高和系统的稳定性更好。

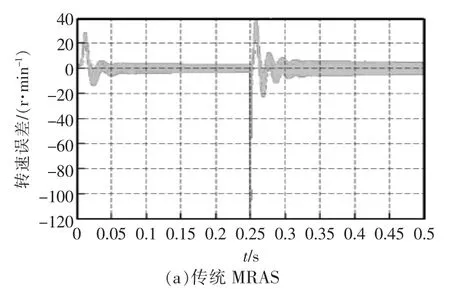
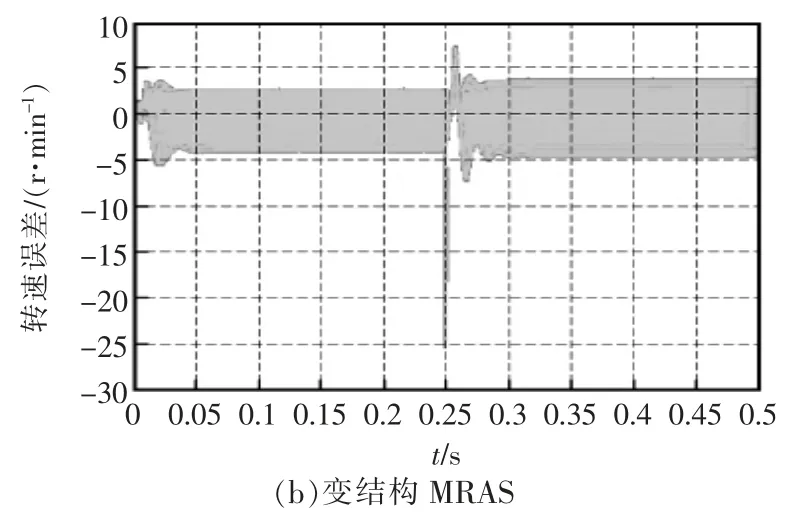
图5 两种MRAS 转速突变误差曲线Fig.5 Abrupt error curves of two kinds ofMRAS rotation speed

试验2 电机给定速度800 r/min，让电机以带2 N·m 的负载启动运行至0.2 s 时给负载一个阶跃信号，使负载从2 N·m 加至20 N·m，验证该系统加负载的抗干扰能力。 两种MRAS 转矩突变转速曲线由图6 所示。由图可见，2 种控制策略都能很好地跟随实际系统，变结构MRAS 在启动后转速曲线较平滑。

图6 两种MRAS 转矩突变转速曲线Fig.6 Curves of two kinds of MRAS torque abrupt speed

MRAS 转矩突变转速误差曲线由图7 所示。 可见，传统MRAS 在启动时转速误差仍比变结构MRAS的转速误差较大；在0.25 s 转矩突变时，传统的转速误差波动为50 r/min，变结构的转速波动较传统的转速波动小，由此也证明了在有负载扰动情况下变结构MRAS 较传统的系统稳定性和抗扰动性能更好。

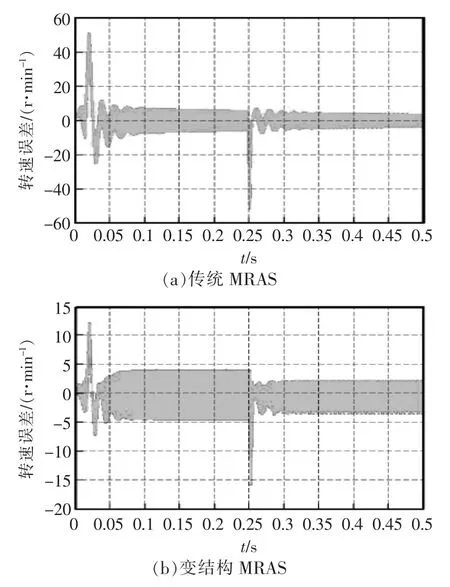
图7 两种MRAS 转矩突变转速误差曲线Fig.7 Error curves of two kinds of MRAS torque abrupt speed

6 结语

将传统的模型参考自适应（MRAS）和新型变结构MRAS 控制策略进行比较，完成了2 种控制策略下内置式永磁同步电机的转速估算的仿真，并验证了在转速、转矩突变下，新型变结构MRAS 的控制策略较传统的控制策略系统的抗干扰能力和鲁棒性更强。 采用新型变结构MRAS 可以省去PI 参数的调节，而且该算法易于实现，在中高速有较好的静态性能、估算精度高和抗干扰性能好，可以满足电动汽车这种频繁转速突变和转矩突变的要求。 因此该新型控制方法对车用的无速度传感器电机进一步研究具有一定参考价值。