基于广义忆阻器的有源带通滤波器仿真与分析

钱辉，钱盛余，任康成，姚肖勇，杨艳

(常州星宇车灯股份有限公司，江苏常州 213022)

0 引言

考虑到利用廉价商用分立元器件实现的简单四阶忆阻混沌电路可作为混沌的数学和实验演示的范例，因此减少动态元件的数量来简化忆阻电路是具有重要价值的研究主题。为了寻找这类四阶忆阻混沌电路，本文作者基于一种广义忆阻模拟器[1]展开研究，该忆阻是一种基于忆阻二极管桥级联LC滤波器实现的广义忆阻。

二阶有源带通滤波器(BPF)可用于生成周期振荡信号。基于有源BPF，文献[2-3]中推演了采用不同非线性特性蔡氏二极管实现的两类蔡氏混沌电路。此外，通过线性耦合一个并联的忆阻-电容滤波器到该有源BPF电路上，文献[4]中拓展了一种四阶忆阻蔡氏混沌电路。有别于此忆阻电路的构建方案[5]，作者利用新提出的改进型广义忆阻器替换有源BPF电路中一颗电阻，直接构建了一种新颖的忆阻BPF电路。该电路方案在汽车未来加密解密方面有着重要的前景应用。

1 忆阻有源带通滤波器

1.1 二极管桥忆阻模拟器

通过简化文献[1]中的LCR二极管桥忆阻，得到的改进后 LC网络级联的二阶广义忆阻器具有更为简单的电路结构，如图1所示。该电路仅由6个动态电路元件组成，分别为4个二极管、1个电容和1个电感。此电路忆阻行为产生的关键机制是对于每对并联二极管的电压约束。

图1所示电路为一个单端网络电路，它有两个输入终端，V指定了终端之间的电压方向，i指定了终端之间的电流流向。假设加在两个动态元素C和L上的电压为VC。

图1 二极管桥忆阻的电路实现

考虑到所选用4个二极管是完全一致的，可以用VDk和iDk分别代表二极管Dk(k=1，2，3，4)的电压和通过电流，其关系可被表示为

iDk=Is(e2ρVDk-1)

(1)

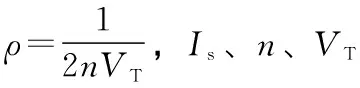
每对并联二极管上的电压有两个恒等式，VD1=VD3和VD2=VD4[6]。通过应用基尔霍夫定律和电路元件的本构关系，可得到相应的电流状态方程为

(2)

同时电压状态方程为

(3)

因此，状态方程组的数学模型和通过电流i可被表示为

(4)

i=g(x,V)V=2Ise-ρVCsinh(ρV)

(5)

这里的x=[VC,iL]T，F(x,V)是一个连续的二维向量函数，且g(x,V)是一个对输入-输出行为进行建模的连续函数，其被表达为

(6)

在整个推导中，等式(4)和等式(5)是描述图1中的单端网络输入输出关系的数学模型，它符合文献[7]中提出的一类广义忆阻器的定义方程。因此，图1所示的单端网络表示了一个二阶广义忆阻器，它的忆阻为g(x,V)。

1.2 忆阻有源带通滤波电路

四阶忆阻有源带通电路具有简单的电路拓扑结构，它仅仅包含了1个运算放大器、3个电容、1个电感和3个电阻[8-9]。文中通过用二极管桥忆阻模拟器替换有源带通滤波电路中的一个电阻，建立起了四阶忆阻有源带通电路，如图2所示。电路中的元件数据参数如表1所示。

图2 四阶忆阻有源带通电路

表1基于忆阻的有源带通滤波器电路参数

参数数值参数数值电容C/nF5.3 电阻R,Ri/Ω50电容C1,C2/nF35电容L/mH20 电阻Rf/kΩ1

1.2.1 Multisim电路仿真及建模

利用Multisim对四阶忆阻有源带通电路进行电路仿真。

分别在电容C2及C、C2及C1、C1及C两端加示波器进行模拟仿真，结果如图3所示。

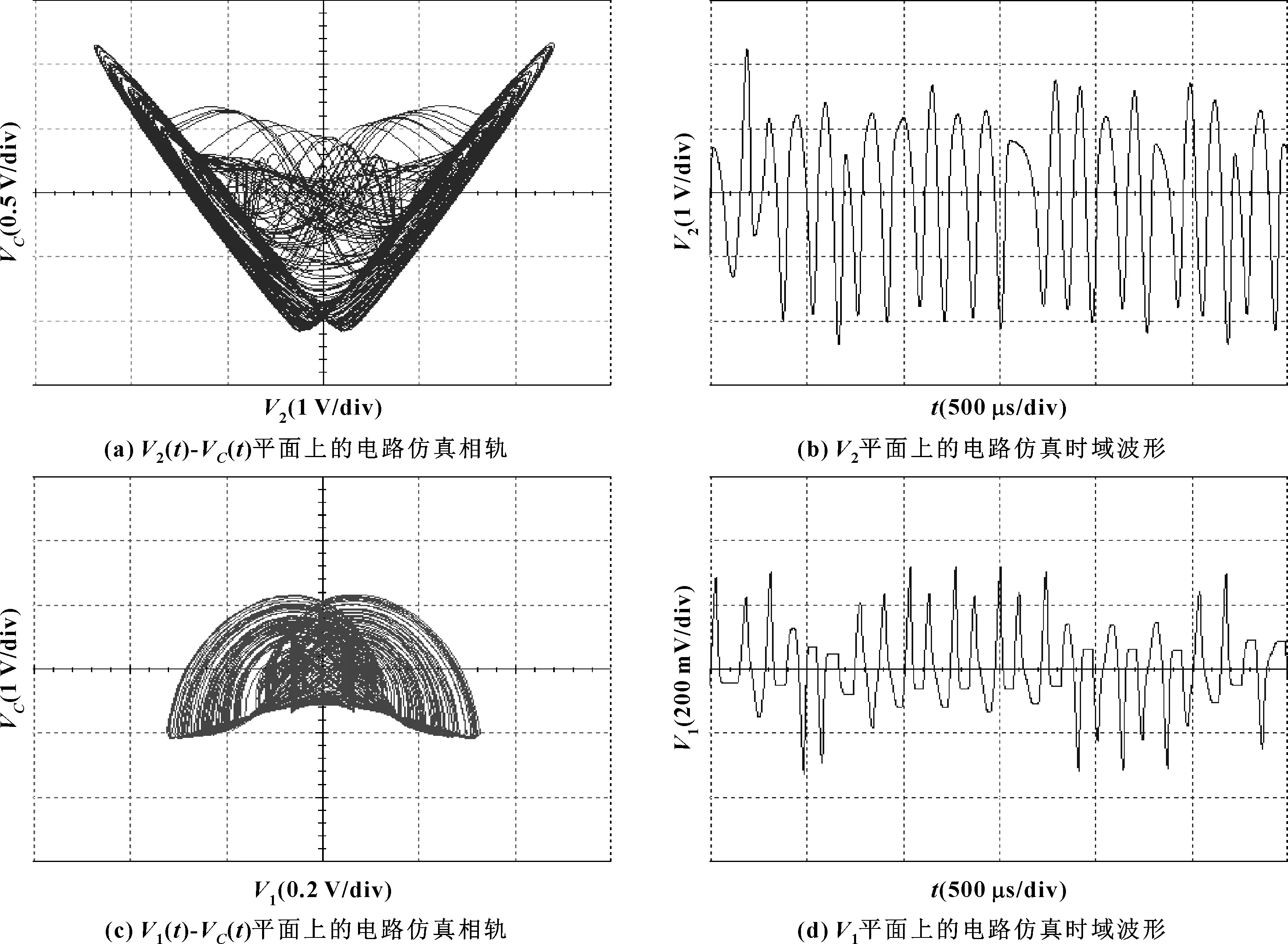
图3 Multisim电路仿真结果

1.2.2 数学建模

此电路中含有4个线性动态参数，分别为蔡氏电路中的电容C1的电压V1、电容C2的电压V2，以及忆阻二极管桥仿真器中的电容C的电压VC、电感L的电流iL，通过应用基尔霍夫定律和电路元件的本构关系[10]，可得到相应的电路状态方程为

(7)

这里的V=V2-V1，且k=Ri/Rf，假设

(8)

等式(7)状态方程能被重新写为量纲为一的方程

(9)

因此，量纲一方程的元素数量减少为3个。

图2中的电路参数如表1所示，4个1N4148二极管参数为Is=5.84 nA、n=1.94、VT=25 mV、ρ=1/(2nVT)，因此，式(8)中的归一化参数可被计算为

a=6.625×10-4,b=6.020 6×10-6,f=d=0.151 4,k=0.05。

1.2.3 稳定性分析

令式(9)的等式左边为零，可得到唯一平衡点S(0,0,0,0)。

系统(9)在平衡点S附近的雅可比矩阵为

(10)

于是，通过求解下面的特征方程，可得平衡点S处的特征值

det(Iλ-J)=0

(11)

相应的，平衡点S处的特征值可被表达为

(12)

对于典型电路参数，代入a=6.625×10-4和k=0.05，可得

λ1=0λ2=0.05λ3,4=±2.573 9

(13)

这意味着S总是一个不稳定的鞍焦点。

1.2.4 典型混沌吸引子

四阶忆阻有源带通电路的参数列于表1，采用型号同样为1N4148的二极管，设定状态变量的初始值为(10-9,0,0,0)，在3个不同平面上的典型混沌吸引子的相轨如图4(a)、(c)所示，时域波形如图4(b)、(d)所示。

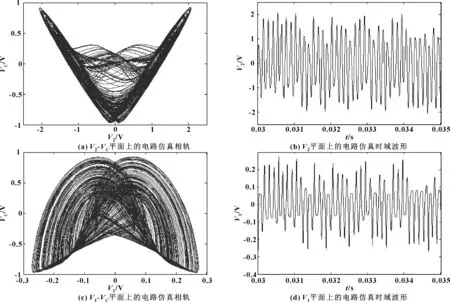
图4 MATLAB电路仿真结果

1.3 动力学行为仿真与分析

1.3.1 随R变化的动力学行为

将电路参数R作为分岔参数。当R逐渐从15 Ω变为85 Ω时，节点电压V1(t)的分岔图如图5所示，R在 [45 Ω,85 Ω]区间内是混沌状态；R在[20 Ω, 38 Ω]区间内是周期状态；R在[38 Ω, 45 Ω]区间内V1(t)分岔共存。

图5显示了具有共存分岔模式的动力学行为，其中红色的轨迹从V1(0)=-1 nV、V2(0)=0 V、V3(0)=0 V、V4(0)=0 V开始，蓝色轨迹对应于V1(0)=1 nV、V2(0)=0 V、V3(0)=0 V、V4(0)=0 V。值得注意的是，要很好地揭示动力学，无论最初的状态是什么，都需要微小的干扰。

对于不同的R值，系统(9)于V2(t)-V1(t)平面上的数值模拟相轨如图6所示，图中红色与蓝色的初始状态和图5所示的相同。这些结果仅仅模拟了系统(9)中的周期、混沌、周期加倍分岔和共存分岔模式的动力学行为。需要注意的是，图6(e)中的混沌吸引子是螺旋结构。

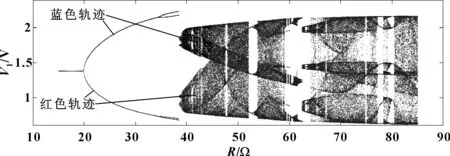
图5 变量V1(t)随R变化的分岔图

图6 在V2(t)-V1(t)平面上的不同R值下的数值仿真相轨图

1.3.2 随L变化的动力学行为

将电路参数L作为分岔参数。当L逐渐从0 mH变为40 mH时，节点电压V1(t)的分岔图如图14所示，L在[3 mH，24 mH]区间是混沌状态，在[34 mH，40 mH]区间是周期状态，在[24 mH，34 mH]区间V1(t)分岔共存。

图7同样显示了具有共存分岔模式的动力学行为，初始也同样为红色的轨迹从V1(0)=-1 nV、V2(0)=0 V、V3(0)=0 V、V4(0)=0 V开始，蓝色的轨迹对应于V1(0)=1 nV、V2(0)=0 V、V3(0)=0 V、V4(0)=0 V。

同样，红色与蓝色初始状态与图7一样的系统(9)于V2(t)-V1(t)平面上的数值模拟相轨图如图8所示。这些结果也仅模拟了系统(9)中的周期、混沌、周期加倍分岔和共存分岔模式的动力学行为。

图7 变量V1(t)随L变化的分岔图

图8 在V2(t)-V1(t)平面上的不同L值下的数值仿真相轨图

2 总结

基于第1节提出的有源带通滤波器蔡氏电路，将其中一个电阻替换为忆阻器，搭建二极管桥忆阻模拟器的电路模型，并对其进行了电路状态的数学建模。通过仿真分析稳定性，展示了电路中的典型混沌吸引子。此外，将R和L作为分岔参数对某个特定平面上的混沌吸引子、共存吸引子、周期吸引子等进行了动力学分析与仿真。