闭式离心叶轮数字化造型算法与结构可视化实现*

（上海交通大学 机械与动力工程学院）

0 引言

叶轮是叶轮机械中的重要部件、气动设计的主要对象之一。在完成整个叶轮机械的热力设计过程中，若能直观实时查看叶轮的子午面、轴向截面及三维几何造型，可帮助设计人员及时了解叶轮流道几何型式，提前判断叶轮加工的可行性和工艺等，有效提高设计效率。这是叶轮机械设计、制造、运行管理全生命周期的数字化过程中的重要一环。叶轮的初始结构参数一般可通过两种方式获得：一是通过设计、计算或实验得到，如获得子午面和轴向截面的主要结构参数；二是通过逆向工程得到，这需要获取叶轮实物，通过精密测量采样获得叶轮结构数据。但二者所获初始数据不一致，前者可能是某些基本几何形状组合或者有限个离散点数据，后者则可能为密集的离散点数据集合，需进一步拟合、插值，才能得到叶轮几何造型。目前，在计算机辅助几何设计（CAGD）中，B样条技术（B-spline）是构造曲线曲面首选。

Woodward[1]提出了一种交互式B样条曲面插值方法，该方法拟合出的曲面更符合工程应用。Liang[2]等人采用迭代计算曲线的控制顶点，提高了拟合曲线的有效性和准确性。Chen[3]等人利用逆向工程获得叶轮曲面的控制顶点网格，输入到CAD软件中构造了叶轮几何造型，规划了加工刀具轨迹，仿真了加工过程。殷明霞[4]等人基于Bezier理论，开发了叶轮二维叶型的可视化流程。刘金梅[5]等人采用非均匀有理B样条技术对叶轮进行了可视化造型。

设计完成后的离心式压缩机通常还需进一步优化，如对叶轮作CFD性能分析。进行CFD前处理时需对叶轮建模，常规方法是人工根据叶轮设计参数在CAD软件中设计和建模，这种方法工作量大、效率低。当叶轮设计参数被修改时，需重新绘制，灵活性差。本文依据B样条曲线曲面理论，对叶轮轮盖、叶片和轮盘型线离散数据进行插值，得到相应的样条曲线曲面，以便在OpenGL中构造三维几何造型，并基于初始图形交换规范，实现叶轮结构数据交互，以在CAD软件中快速建模。

1 闭式离心叶轮结构特点

叶轮是离心式压缩机的重要运动结构，其性能直接影响压缩机效率。按外形结构主要可分为闭式、半开式和开式。通常，闭式叶轮效率相对较高，应用也最广泛，结构上呈“三明治”状，从工质流动方向看，依次由轮盘、叶片和轮盖组成，轮盘和轮盖将叶片夹于中间。

通过模化法、流道法、效率法等离心式压缩机热力设计方法可计算出闭式离心叶轮的几何结构参数，总结见表1。由此可得如图1所示的典型闭式离心叶轮子午面和轴向截面图。

表1 闭式离心叶轮主要几何结构参数Tab.1 Main geometric parameters of a shrouded centrifugal impeller

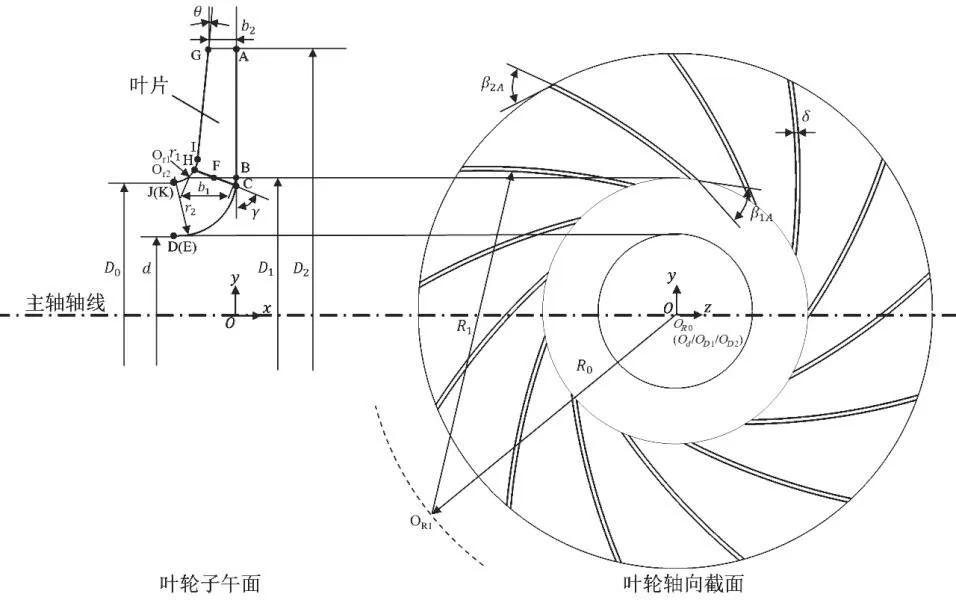
图1 闭式离心叶轮子午面和轴向截面Fig.1 Meridian(left)and axial(right)section of a shrouded centrifugal impeller

2 闭式离心叶轮造型方法

2.1 非均匀有理B样条曲线与曲面

传统B样条无法精确表示抛物线、抛物面以外的二次曲线曲面，非均匀有理B样条（NURBS）可妥善解决。一个k次NURBS曲线可表示为一个分段有理多项式函数：

式中，σi(i =0,1,…,n)为对应控制顶点Pi(i =0,1,…,n)的权因子。

推广至曲面表示为：

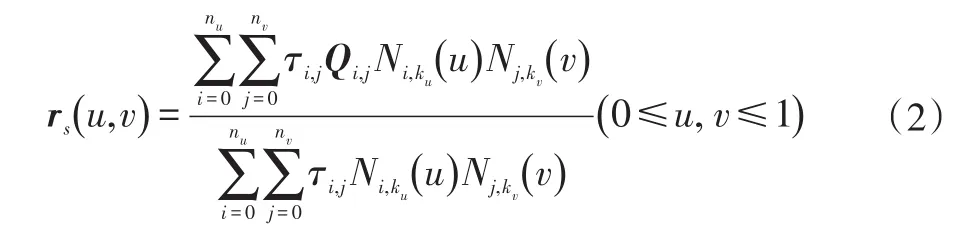
式中，τi,j(i = 0,1,…,nu;j=0,1,…,nv)为控制网格顶点Qi,j(i = 0,1,…,nu;j=0,1,…,nv)的权因子；Ni,ku(u)表示为节点序列{ui}(i = 0,1,2,…,nu+ku+1) 上第i个ku次B样条基函数；Nj,kv(v)表示为节点序列{vj}( j =0,1,2,…,nv+kv+1)上第j个kv次B样条基函数。

当权因子τi,j均为1时，NURBS曲线或曲面退化为非有理B样条曲线或曲面。

2.2 非均匀有理B样条单位整圆和旋转曲面

NURBS中有多种二次表示方案用于描述单位整圆[6]，本文使用九顶点外切正方形表示方案，其效果在多种方案中表现最好。如图2，图中Vi为控制顶点，ωi为权因子，T为节点序列。

图2 九顶点外切正方形表示方法Fig.2 Representation of nine vertex circumscribed square

以定义为式（1），在xy平面上的k次NURBS曲线为母线，绕z轴旋转生成的旋转曲面可表示为如式（2）的NURBS曲面，则曲面的控制顶点和权因子分别为[7]

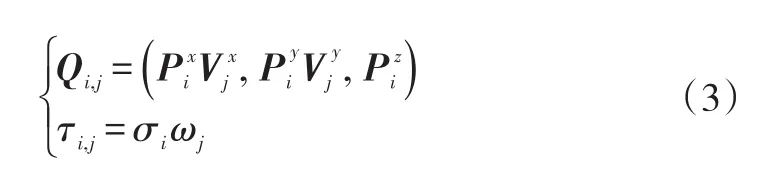
式中，Vj为xy平面上NURBS单位整圆的控制顶点；ωj为单位整圆的权因子，与图2相同；Pi，Vj的上标表示对应的x,y,z坐标。

2.3 非均匀有理B样条插值算法

根据给定数据点，构造一条B样条曲线使其通过给定数据点的拟合方法，称为B样条曲线插值。构造一条插值B样条曲线需确定其节点序列和控制顶点。通常使用非均匀节点序列，这样生成的曲线更精确。

对于已知的数据点列{Pi}(i =0,1,2,…,n )，采用累积弦长法[8]确定非均匀B样条曲线的节点序列{ti}(i = 0,1,…,n+6)

式（7）共包含 n+1个方程，若要求解所有的 n+3个控制顶点Vi，则需额外补充两个方程。常用的边界条件有：切矢条件、自由端点条件、抛物线条件等[9]。本文使用Bessel切矢方法[6]，主要思路是通过插值一条过三点Pi-1,Pi,Pi+1的抛物线，计算抛物线上三点的导数，从而得到三点的估算切矢，具体方法为：

设Pi-1,Pi,Pi+1对应的参数为：

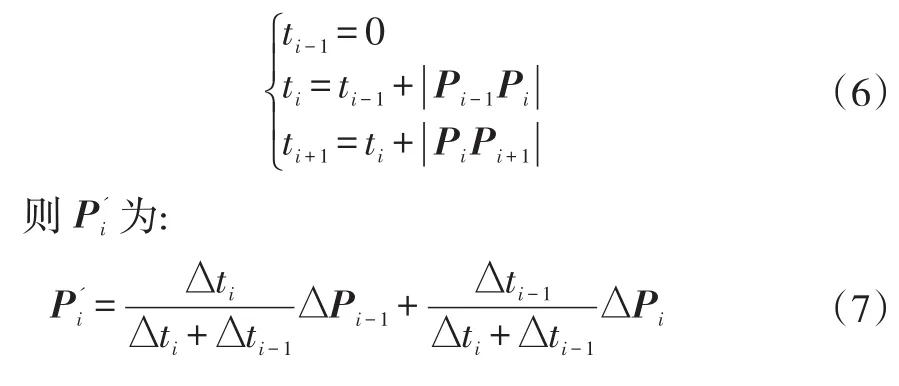
式中，Δti=ti+1-ti，ΔPi=(Pi+1-Pi)/Δti。

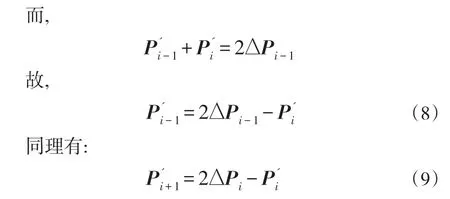
联立式（4）、（7）、（8）可得 n+3个方程，由此可唯一确定所有的n+3个控制顶点Vi。由于该n+3个方程构成三对角矩阵，可使用追赶法求解。

3 闭式离心叶轮几何造型绘制

3.1 二维几何造型

闭式离心叶轮的二维几何造型包括子午面和轴向截面。

1）子午面

将图3所示叶轮子午面中标出的关键点全部确定后，即可确定子午面轮盖和轮盘的数据点，进而可按NURBS插值方法对数据点插值，得到描述轮盖和轮盘的NURBS曲线。

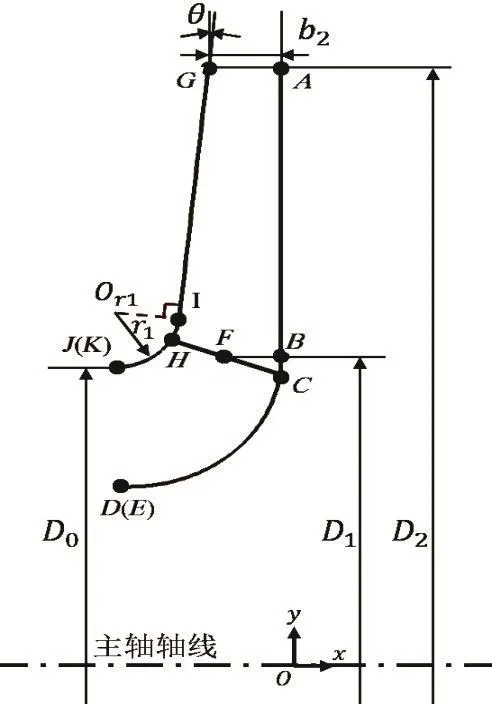
图3 叶轮子午面示意图Fig.3 Schematics of meridional surface of an impeller

2）轴向截面

轴向截面主要由圆和圆弧组成。在绘制叶片圆弧段时，如图4，由于圆OR1,i( )i=1,2,…,n,n为叶片数 与圆OD1和圆OD2共有四个交点，可作两段叶片，但对于每一个圆OR1,i，仅需其中一段，且相对位置应一致，即同为弧P1,iP2,i或弧P3,iP4,i。根据向量积，可知：

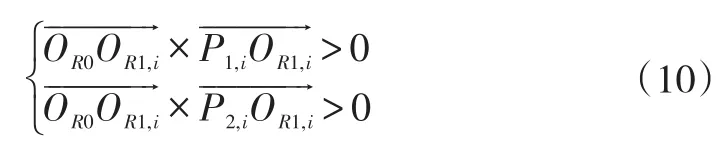
和

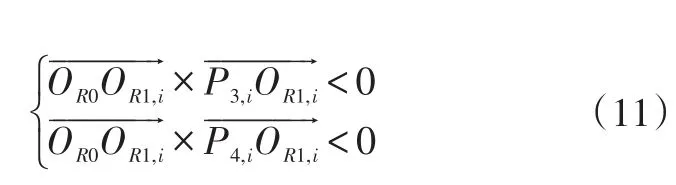
由向量积符号一致性可判断并作出相对位置一致的叶片圆弧段。

图4 叶轮轴向截面示意图Fig.4 Schematics of axial section of an impeller

3.2 三维几何造型

1）轮盖和轮盘曲面

轮盖和轮盘是以子午面轮盖和轮盘曲线为母线的旋转曲面，曲面以流体进口方向的整圆为u方向，以子午面轮盖和轮盘曲线段为v方向绘制NURBS曲面。具体为：将v方向上的控制顶点沿u方向的控制顶点遍历计算，按前述方法确定旋转面的控制顶点网格，进而得到轮盘和轮盖曲面，如图5。

2）叶片压力面和吸力面

绘制叶片压力面和吸力面需获取叶片轮盖线和叶片轮盘线，两个曲面共需四条曲线。如图6，在叶片轮盖线或叶片轮盘线取一点P(xtag,dist)，dist为点P到主轴轴线的距离。在叶轮轴向截面上，以dist为半径，原点为圆心作圆，与叶片曲线段相交于点Q(ytag,ztag)，点Q在三维空间中的x坐标为xtag，故点Q在三维空间中的坐标应为(xtag,ytag,ztag)，即为子午面内点P对应在三维空间中叶片压力面或吸力面的空间点。

图5 轮盘与轮盖曲面几何造型Fig.5 Geometric modeling of hub(a)and shroud(b)surface

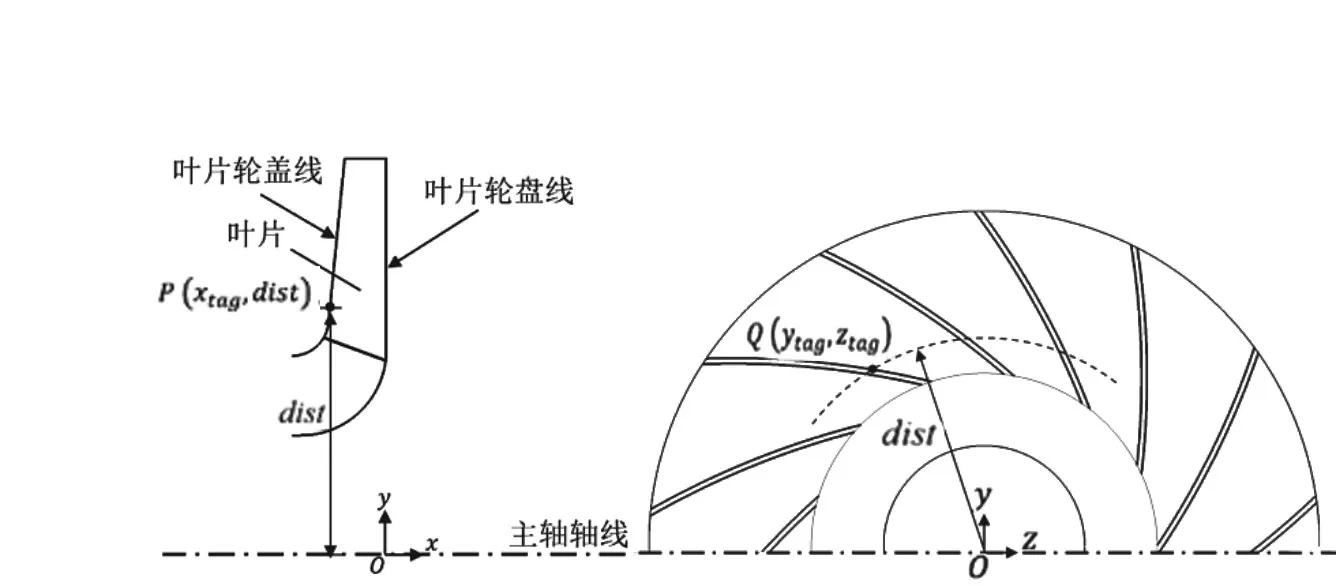
图6 叶片压力面与吸力面计算示意图Fig.6 Calculation schematics of pressure and suction surface of blades

以压力面为例，得到叶片轮盖线和轮盘线后，取叶片轮盖线和轮盘线的端点为u方向，以叶片轮盖线和轮盘线为v方向，绘制NURBS曲面。u方向上仅有两个控制点，即叶片轮盖线和轮盘线的端点，对应的节点序列为U=[0,0,1,1]。绘制的叶片压力面和吸力面如图7所示。

图7 叶片压力面与吸力面几何造型Fig.7 Geometric modeling of pressure and suction surface of blades

3.3 可视化造型检验

以某离心式压缩机叶轮为例，在压缩机进口总压、总温，压缩机出口总压、质量流量确定的条件下，设计得到基本气动参数，基于OpenGL将叶轮几何结构参数绘制得到的三维造型如图8所示。

图8 某闭式离心叶轮几何造型Fig.8 Geometric modeling of a shrouded centrifugal impeller

4 几何数据交互

将叶轮数据输出成CAD软件可识别的通用文件有多种方法，本文使用初始图形交换规范（IGES）格式和文本（TXT）格式。

4.1 IGES输出方法

IGES固定格式文件被分为若干段，每段由若干行组成，每行有80列，一个ASCII字符占一列，其中1～72列是特定的数据域，第73列是标识字母代码，见表2，第74～80列是所在行在所在段的序号，序号在每段中从1开始，每行加1。

对于离心叶轮几何造型，使用到的几何类型有点、直线、NURBS曲线和曲面。

表2 IGES固定格式数据段及其标识字母代码Tab.2 Fixed format data segment and its identification code

1）点的参数格式

类型号为116，参数数据段的数据依次为：类型号（116）、点的X，Y，Z坐标、指向用于规定显示符号的实体的指针或0，共5个。

2）直线的参数格式

类型号为110，数据依次为：类型号（110）、起点的X，Y，Z坐标、终点的X，Y，Z坐标，共7个。

3）NURBS曲线的参数格式

类型号为126，数据依次为：类型号（126）、控制顶点数量、基函数阶数（次数+1）、曲线是否为平面曲线、曲线的开闭、曲线为有理或多项式、曲线是否周期、节点序列（若干个）、控制顶点权因子（若干个）、控制顶点三维坐标（若干个）、始参数值（0）、终参数值（1）、当曲线为平面曲线时的单位法矢。

4）NURBS曲面的参数格式

类型号为128，数据依次为：类型号（128）、u方向控制顶点数量、v方向控制顶点数量、u方向基函数阶数、v方向基函数阶数、曲线在u方向和v方向的开闭（2个）、曲线为有理或多项式、曲线在u方向和v方向是否周期（2个）、u方向节点序列（若干个）、v方向节点序列（若干个）、控制顶点权因子（若干个）、控制顶点三维坐标（若干个）、u方向始参数值（0）、u方向终参数值（1）、v方向始参数值（0）、v方向终参数值（1）。

需注意某些后置处理器，如ANSYS BladeGen，对一行数据的完整识别止于换行符，在结束段的末端应添加一个换行符以使该行被完整识别。

4.2 TXT输出方法

TXT作为一种输出格式，只能输出点。若需要输出NURBS曲线，则应对其进行较高密度的离散化，然后以TXT输出。输出格式为：每行包含一个点的三维坐标数据，以X坐标、Y坐标、Z坐标的顺序排列，坐标之间以空格或“,”间隔。TXT的输出较IGES简便，但在导入CAD软件时，需再处理。因此，应优先选择以IGES输出。

4.3 几何造型参数反算

本文输出的叶轮曲线造型，可通过反算得到原始几何结构参数，实现参数的双向交互。根据NURBS曲线性质，叶轮子午面轮盘和轮盖曲线的端点与其NURBS曲线的首尾控制顶点重合且相切，如图9，即Ctrl1Ctrl2和Ctrl4Ctrl5分别与曲线两端相切，可确定子午面各关键点的坐标位置，进而可知直径D0，D1，D2，d ，半径 r1，r2，宽度 b1，b2，倾角 θ等参数，参见图3。叶轮轴向截面的叶片圆弧也可根据其NURBS性质确定半径R1，R2，再联立二者可确定进出口安装角 β1A，β2A，从而得到叶轮的主要结构参数数据。

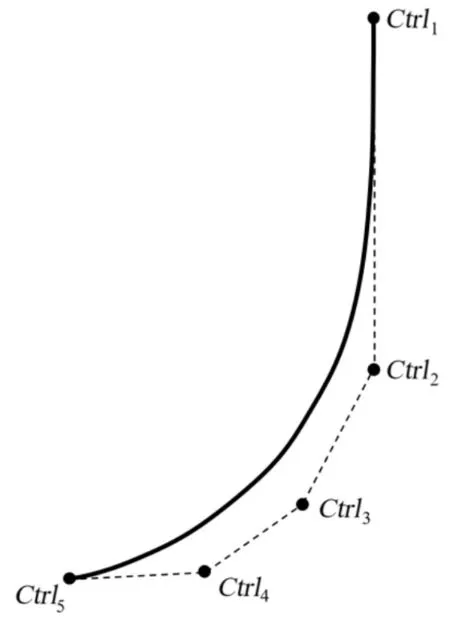
图9 NURBS曲线及控制顶点示意图Fig.9 Schematics of NURBS curve and control vertex

5 结论

本文基于离心叶轮气动设计过程生成的结构参数，采用非均匀有理B样条技术，构建了闭式离心式压缩机叶轮的二维和三维数字化几何造型，包括子午面、轴向截面、轮盘、轮盖、叶片吸力面和压力面等，继而以某离心式压缩机叶轮设计中的参数为例，实现了该叶轮结构的可视化。进一步结合IGES数据交换规范，实现了叶轮几何与CAD软件之间的数据交互，联接了叶轮设计与CAD软件建模。

该方法完善了叶轮生命周期的数字化过程环节，有效缩短了设计周期，提高了设计效率，并可进一步推广至其他类型压缩机叶轮。