机器人视觉装配中的精确定位策略研究

，，

(上海交通大学机械与动力工程学院,上海 200240)

0 引言

在传统工业生产中大量应用的是基于传送带的生产模式，固定的流水线适合大规模量产，但面对不同产品的生产需求，传统的生产线需要进行改造以适应新的装配工艺和工序，存在适应性差的情况。同时增加了制造成本，影响到生产效益[1]。随着工业4.0的提出，生产的个性化和灵活性要求生产线具有高度柔性的特点，可以灵活地处理组装零件和工艺顺序的变化[2]。同时无人驾驶运输系统快速发展，通过将原本只是用作物料搬运的小车和机器人进行深度融合，打破现有的固定流水线，取而代之的是，载着工件的自动导航小车从一个机器人工位移动到另一个机器人工位，形成一条移动的生产线。这种方式可以适应个性化需求，提升生产线的柔性和自主性。

但由于自动导航小车每次到达机器人工位时的位置存在不确定性，给机器人的装配任务引入了偏差，即便使用了定位板等辅助技术来提高自动导航小车的定位精度，仍存在3～5 cm的定位偏差，无法满足精度要求高的任务，如自动打螺钉、插销孔等[3]。为校正定位偏差，可运用机器视觉技术，通过在机器人的末端安装工业相机，对到达机器人工位小车上的多个定位孔进行识别，并计算转换到全局坐标系下，结合多组匹配点来计算小车实际位姿，进而调整机器人抓取的目标位置来实现既定的装配任务。

在此，研究了利用机器视觉技术进行位置校正的各个关键环节，推导了目标位置的计算公式及小车位姿的校正算法。在此基础上分析过程中可能引入的误差，并提出了一系列消除偏差、提高精度的策略，最后通过对比实验验证了误差消除算法的效果，为视觉引导下的机器人装配工作提供了依据。

1 机器人视觉装配系统

本文中的机器人视觉装配系统包括工控机、工业机器人及末端执行器、工业相机及光源、自动导航移动平台及其上定位孔等。系统整体如图1所示。

图1 机器人视觉装配系统

视觉校正过程主要分为2步：第1步，从源图像中识别出定位孔中心并计算定位孔的实际坐标；第2步，根据多个定位孔的位置计算小车实际位姿相对于基准位姿的转换关系。

分析定位孔的识别和计算过程，其中涉及到了坐标在多个参考系间的转换，过程如图2所示。

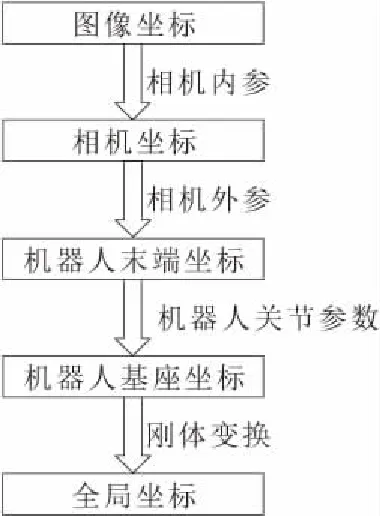
图2 坐标间的转换关系

根据以上得到的每个定位孔在全局坐标系下的位置，通过多组匹配点校准计算最优的旋转平移矩阵，即当前小车位姿相对于基准位姿的关系，并利用该矩阵计算装配工件的实际位置，控制机器人到目标点进行装配作业。

2 视觉定位算法

机器视觉系统中涉及多个坐标系间的转换，包括像素坐标系(u,v)，相机坐标系(xc,yc,zc)和世界坐标系(xw,yw,zw)[4]。各坐标系间的关系如图3所示。

图3 坐标系的关系转换

相机标定的参数可以分为内参和外参。相机内参，顾名思义描述相机的内部属性，如相机的焦距、像素点大小和相机畸变属性等。内参用于像素坐标系和相机坐标系间的转换。外参描述相机的空间位置，也即相机坐标相对于世界坐标系的旋转和平移。

2.1 相机参数标定

相机内参矩阵定义为

(1)

fx和fy为以像素为单位的焦距参数；γ为x轴和y轴间的倾斜系数，其值通常为0；u0和v0为主点，即理想条件下图像的中点。相机内参的标定可以采用张正友标定法，对单平面棋盘格采集n幅图像，每幅图像中有棋盘格角点m个，利用多参数非线性系统优化问题的Levenberg-Marquardt算法[5]进行迭代求最优解。相机内参标定有成熟的算法和标定工具，根据极大似然估计得到的内参在相机定焦的情况下相当稳定。利用内参可以计算出目标物体在相机坐标系下的位置。计算公式为

(2)

相机外参的标定即手眼标定，涉及到相机、机器人基座、末端执行器和标定板坐标系之间的关系。根据相机是与机器人末端或是与基座固连，可以分为eye on hand和eye to hand 2种方式[6]。本文采用eye on hand模式，坐标系之间的关系如图4所示。相机和机器人末端固定在一起，标定板和机器人基坐标系固定在一起。在这种关系下，机器人移动过程中任意2个位姿，标定板和底座的关系始终不变，求解的量为相机和机器人末端之间的关系。

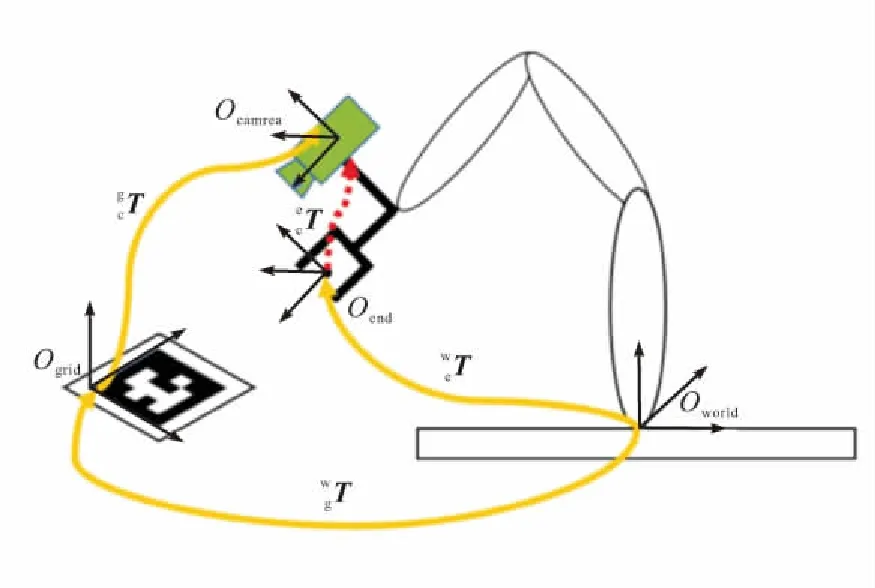
图4 手眼标定坐标系的转换

本文使用arUco标定板，该标记的外围都有1组黑色边框，同时内部有确定该标记ID的二维矩阵，黑色的边框能加速标记在图像中的检测速度，内部的二维编码能唯一识别该标记，同时进行错误检测和错误修复。标记的大小确定了内部矩阵的大小，例如4×4大小的标记有16个bit。其检测结果返回图片中4个角点的位置以及标记的ID号。利用OpenCV中的solvePnP函数可以得到标定板相对于相机坐标系的齐次矩阵。为了得到精确的手眼关系，相机在不同位姿对标定板拍摄17～20张图片进行计算。任意2次拍摄满足以下约束：

(4)

(5)

(6)

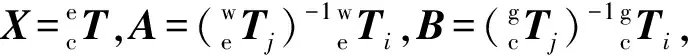
AX=XB

(7)

A为相邻2次运动中机器人末端关节的变换关系；B为相邻2次运动时相机坐标的相对运动。以上方程为手眼标定的最终求解方程，可以通过Tsai-Lenz方法[7]计算转换矩阵X。求解得到结果用四元数q=[wxyz]T和向量t=[δxδyδz]T表示。其中四元数的定义满足

|q|2=w2+x2+y2+z2=1

(8)

四元数转换为旋转矩阵的公式为

(9)

则相机坐标系和末端坐标系的手眼关系为

(10)

2.2 位姿校正算法

上一小节完成了定位孔在全局坐标系中坐标的计算推导。接着根据多个定位孔的计算结果，来估计小车实际位姿相对于基准位姿的旋转平移矩阵。基准位姿和实际位姿如图5所示，虚线部分表示AGV基准位姿及其4个定位孔的位置，实线部分表示当前AGV到达机器人工位时的实际位姿，十字形标记表示待装配工件。

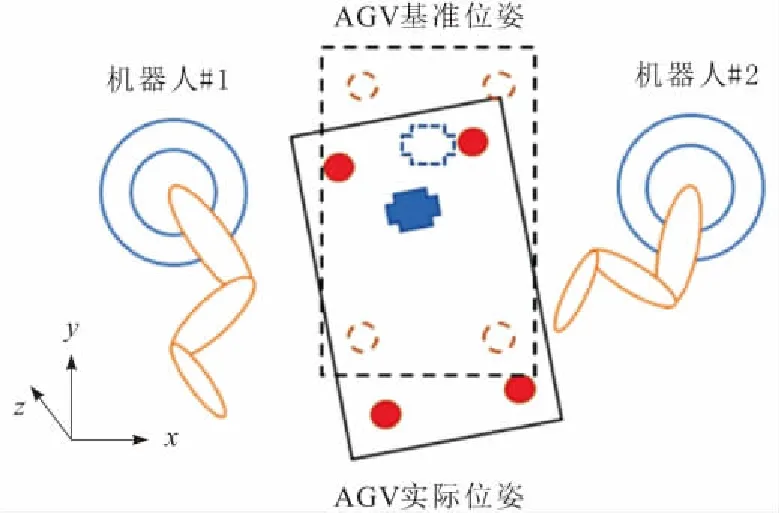
图5 AGV实际位姿

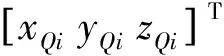
(11)

对于所有匹配点，满足

(12)

简记为Q=MP，求解得M=QP-1。刚性变换矩阵M包含6个参数，通过视觉识别并计算得到的4个定位孔位置包含12个已知量，所以存在冗余，且可以得到多组可行解。将每一对匹配点的欧氏距离作为误差目标函数，利用SVD分解求出R和T，使得误差目标函数最小。

在得到M的最优估计后，利用该旋转平移矩阵计算出待装配工件的实际位置，以此作为视觉校正后的目标位置控制机器人进行装配工作。

3 误差及消除策略

3.1 误差分析

本节分析在计算目标位置的各阶段中可能引入误差的情形。

首先，相机获取到1张原始图像，应用机器视觉算法从源图像中找到定位孔的中心位置。本文设计了一种基于特征的模板匹配算法，利用边缘的梯度方向作为特征，训练出一系列不同角度不同尺寸的模板。在识别时将图像中的特征与这一系列模板进行匹配，根据匹配率筛选出符合条件的模板。可能会出现多个相似模板同时匹配的情况，例如大小十分接近，转角存在微小差异的模板，如图6所示。若从其中随机取1个模板，虽然和实际的中心位置只有几个像素的偏差，但这些误差经过相机内参和外参的传递，在实际计算目标位置中会被放大，甚至会因此造成装配任务的失败。

图6 多个相似模板同时匹配上

其次，手眼标定计算相机外参齐次矩阵的结果受标定过程中采样点的选择影响大，包括拍摄标定板采样点的数量及相对位置关系等。计算手眼标定矩阵采用Tsai提出的旋转轴-旋转角方法[7]，在优化阶段以匹配点欧氏距离作为误差目标函数，其中用到了最小二乘法的思想。如果某一次标定板局部或全部偏出相机视野则会出现标定板识别错误，导致数据不可用，1组点的明显偏离会对拟合结果造成非常大的偏差。

3.2 误差消除策略

针对上一小节中的误差分析，本文提出相应的误差消除策略，减小可能引入的误差，提高目标位置计算的精度。

首先，在图像识别阶段，利用模板匹配筛选出1组特征匹配度高的模板后，利用圆孔识别的特殊性，选择最靠近中心尺寸最小的圆作为识别结果，如图7所示。

图7 对多个模板进行优选

此外，如果在视野内出现多个圆孔干扰项，如待装配工件上的螺钉孔，则根据孔的位置与相机视野中心的距离，并结合识别孔与实际定位孔的大小差别来进行干扰项的过滤。

其次，手眼标定时增加拍摄标定板的数量，用更多的输入点来优化外参矩阵的准确度。同时调整机器人不同末端姿态，改变相机和标定板之间的旋转和平移关系。例如，对于每一组采样点的选择，控制机器人末端的位移达到5 mm，旋转角度达到10°，从不同视角进行拍摄。对于误检的标定板，采用RANSAC算法通过多次迭代将不匹配的输入点进行剔除，最后利用可靠的位置点进行手眼标定矩阵的计算。

3.3 模型简化

由于本文应用场景的特殊性，即AGV小车的高度在过程中不会发生变化，所以定位孔在z方向上恒为常数，故位姿校正可以简化为2个平面间的刚性变换过程。三维场景退化为二维后，矩阵M中需要确定的参数缩减到3个，即1个旋转角和2个平移量。同时，数据流的传递过程也可以得到简化，如图8所示，直接从相机坐标系转换到全局坐标系。

图8 二维空间下的坐标转换关系

以上做法的优势有2点：一是省去了中间转换到机器人基坐标系再转换到世界坐标系的过程，简化了问题的复杂度和计算的过程；二是由于坐标系的直接转换而带来误差的减小，同时保证了精度的可靠性。

这种情况下，相机外参的标定即为相机坐标系x-y平面到世界坐标系x-y平面的刚体变换矩阵的求解。如图9所示，利用机器人定位的高精度，控制机器人分别在x方向和y方向上移动指定的距离，分别求出定位孔在相机坐标系下的位置，以此计算2个平面间的变换矩阵。

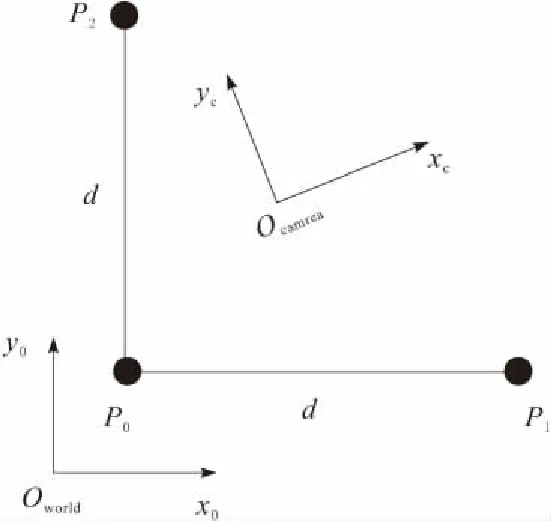
图9 相机坐标系与世界坐标系的关系

Mw=RMc

(13)

容易计算求解得到旋转矩阵R。通过该矩阵可将定位孔的坐标从相机坐标系的x-y平面直接转换到全局坐标系x-y平面下。在此基础上进行后续计算，整个视觉校正过程得到了简化，同时保证了定位精度。

4 实验验证

通过实验，对以上提出的提高视觉定位精度的方法进行验证。实验原理如图10所示，通过测量视觉校正计算后得到位置P′和实际位置P在世界坐标系x-y平面上的偏差，来反映视觉校正结果的精确度。

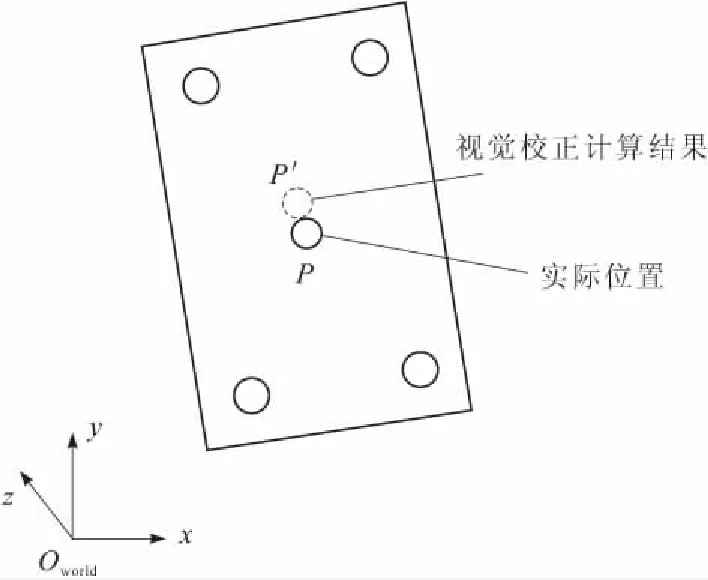
图10 测量视觉校正结果的偏差

本文设计了2组实验，一组是采用普通视觉标定流程得到的参数，另一组是采用误差消除策略改进后标定得到的参数。按上文反映精度的方法测量视觉校正得到的位置与实际位置的偏差值，将最终的偏差结果表现在同一张图中，如图11所示，横坐标为x方向上的偏差，纵坐标为y方向上的偏差。

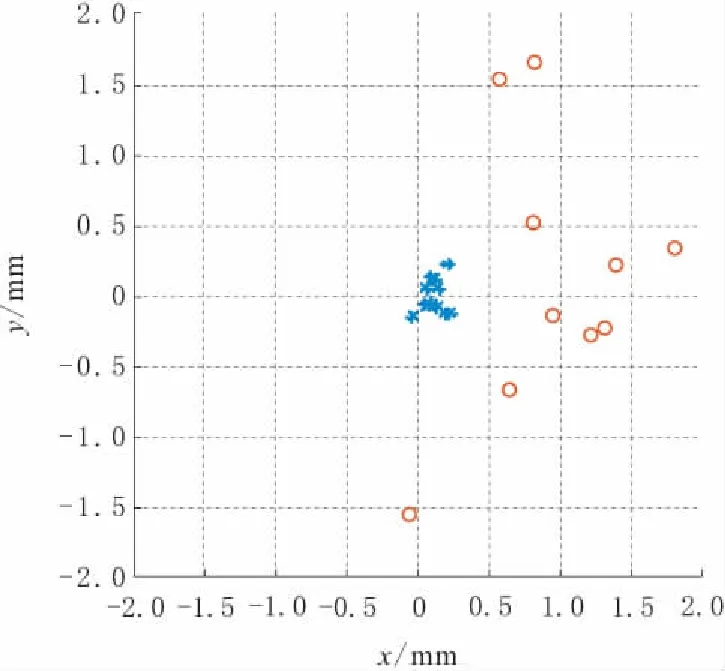
图11 消除偏差策略实验效果

图11中，圆圈表示直接用标定结果计算的偏差，星号表示误差消除算法改进后的结果。可以看出偏差问题得到了明显的改善，直接标定结果的偏差值均方根为1.428 9 mm，改进后的偏差值均方根为0.188 1 mm。2组数据在y方向上偏差分布均匀，在x方向上多数出现偏大，分析原因可能是相机坐标系z轴与世界坐标系z轴的平行程度存在微小偏差导致。同时测量数据显示，应用误差消除算法后定位偏差可以控制在0.5 mm以内，满足精度要求高的装配需求。

5 结束语

通过机器人视觉系统，完成装配目标位置的精确定位和校正。在分析了相机标定原理的基础上，通过内参标定和手眼标定计算出各坐标系间转换的齐次矩阵。分析坐标从源图像到世界坐标系的计算过程中可能引入的误差，并提出相应的误差消除策略。针对定位孔识别的特殊性，提出了简化计算模型和坐标转换过程的算法，最后通过实验验证了误差消除策略的可行性，精度提升效果明显，为机器人视觉装配工作提供了依据。