一种椭圆弧面轴承的变流域结构化动网格方法
,,,,
(1.中国核动力研究设计院核反应堆系统设计技术重点实验室,四川 成都 610231;2.中国石油天然气管道工程有限公司机械室,河北 廊坊 065000)
0 引言
椭圆轴承由于其良好的稳定性和承载能力,在大、中容量汽轮机组中得到广泛运用。由于轴颈在轴瓦内的绝对偏心距增大,使得在上、下部轴瓦都可以形成油楔。在上油楔的油膜力作用下,轴承运行的稳定性得到改善。传统意义上的椭圆轴承为了减小加工难度,一般采用2块圆弧形轴瓦构成,2个轴瓦的中心与椭圆轴承的几何中心之间存在一定的预偏心距,以此来形成上下2部油楔。
早期的轴承研究由于计算水平和理论水平的限制,只能通过求解简化的模型来对滑动轴承进行研究。如一些学者[1-3]基于对雷诺方程的求解,来模拟椭圆轴承油膜的一系列特性。但是由于雷诺方程是对N-S方程的简化,其中忽略了油膜曲率和惯性项等因素,因此这些模型从理论上就与实际存在一定的误差。虽然依靠该模型取得了大量成果,但是始终不能对轴承的真实油膜特性进行最彻底的反映。正因为如此,越来越多的学者选择通过直接求解N-S 方程的方法来开展轴承研究,希望能够更准确地模拟滑动轴承的相关特性。
近年来,随着计算机性能的提高和CFD技术的发展,滑动轴承的仿真模拟技术获得了很大的进步。一些学者先后建立了圆轴承的三维CFD模型[4-8],并且为了研究滑动轴承油膜瞬态特性,动网格技术被迅速引入到轴承计算中。甚至对于椭圆轴承,孙丹[9]、李强[10]等利用 CFD 动网格技术对传统椭圆轴承动力特性进行了研究。但是,这样的方法仅仅适用于传统椭圆轴承上下2片圆弧轴瓦偏心的简单几何结构,对椭圆弧面轴承并不适用。
目前,椭圆轴承相关研究主要都是针对传统椭圆轴承开展的。随着机械加工水平的提高,加工椭圆弧面的滑动轴承已经可以实现,因此椭圆弧面轴承与传统椭圆轴承的性能对比研究亟待开展。为了对椭圆弧面轴承进行仿真,本文提出一种针对椭圆弧面轴承的变流域结构化动网格方法,保证椭圆弧面轴承中油膜间隙网格随着轴颈的动态移动而规律性变化,在此基础上建立多流域-转子动力学方程耦合,计算得到轴心轨迹、压力分布等参数,与传统椭圆轴承进行了对比。
1 椭圆弧面轴承变流域结构化动网格方法
文献[10]提出了一种适用于普通滑动轴承的变流域结构化动网格方法。本文采用该方法来对传统椭圆轴承进行模拟,但这样的方法对椭圆弧面轴承并不适用,因此提出适用于椭圆弧面轴承的变流域结构化动网格方法。
轴颈扰动时椭圆弧面轴承油膜中网格位置变化示意如图1所示。椭圆弧面轴承的润滑流场采用结构化网格进行划分,在结构化网格的基础上,本文提出了一种适用于椭圆弧面轴承瞬态流场计算的变流域动网格技术。需要说明的是,为了更好地展示网格的移动情况,图1中的轴承间隙被放大。在网格划分时,以图1中5层网格为例,每层网格均分布在不同的椭圆面上:最内1层(第0层)网格在轴颈面上,为圆筒形;最外1层(第5层)网格在轴承面上,为椭圆形。椭圆面上的网格随着椭圆面作刚性移动。这样处理之后,因为轴承润滑流场(除去油槽)中的所有节点都是按照一定规则排列分布的,使得每个节点的位置坐标都可以通过计算得到。当轴颈涡动时,流场最内圈上的所有节点都随着轴颈一起移动,最外圈及油槽上的节点保持不动,中间的节点则根据所处位置按一定的算法移动不同的距离。
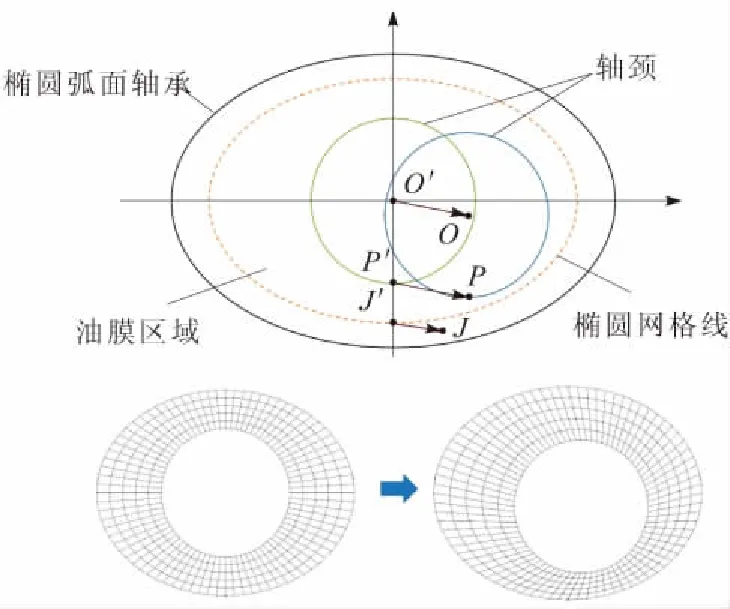
图1 轴承间隙周向网格移动示意
假设,油膜流域网格第j层均分布在如下椭圆上:
(1)
RLj和RSj分别为椭圆长短轴半径;xbj和ybj为当前椭圆中心的位置,xbj和ybj的位置可由轴颈位移计算得到。因为轴颈面上的节点移动距离是最大的,而轴承面上节点是静止不动的,所以椭圆中心移动的距离是从轴颈面到轴承面线性递减的。对于第j层椭圆中心位置为
(2)
xd和yd为轴颈位移;N为网格层数。
网格的运动可以通过Fluent UDF中相关的宏来实现,利用宏指令可以按规律将节点移至新的位置。由于采用了上述的网格移动方法,保证了网格变化过程中无论什么节点的数量还是节点间的拓扑关系都不会发生变化,而且保证了在成千上万次的移动之后网格质量完好,确保计算的稳定性和结果的精确。
2 多流场-转子动力学耦合计算方法
由于仅对传统椭圆轴承和椭圆弧面轴承的转子系统动力学行为作定性对比分析,为了简化,假设为转子由2个相同的滑动轴承来提供支撑,且不考虑转子轴颈段的弯曲和倾斜。同时为了提高计算效率,建立了如图2所示的镜像滑动轴承流场与转子动力学间的耦合计算。在每个时间步长开始时,首先通过对油膜压力进行积分获得的非线性油膜力Fx和Fy,同时将油膜力和瞬态计算的时间t及时间步长Δt通过数据文件的形式传送给Fortran程序,进行转子动力学计算。Fortran程序通过对转子动力学方程进行NewMark积分求解,最终得到轴颈的位置和速度,同样通过数据文件的形式将其传入Fluent UDF,而Fluent通过宏DEFINE_GRID_MOTION根据读入的轴颈位移,利用前述动网格技术来对油膜流域进行网格坐标更新,然后进入流场迭代计算,以此循环更新直至稳定。
对转子而言,由于轴颈在油膜中涡动,因此轴颈的旋转中心一直在随着轴颈涡动而不断变化位置。为了正确设置轴颈表面速度,借鉴文献[10]的思路,通过DEFINE_PROFILE宏计算轴颈表面节点的表面速度、轴颈平动速度和合速度,并将计算出的速度值赋给轴颈表面节点。
vx=(yp-yd)·ω,vy=(xp-xd)·ω
(3)
xp,yp为轴颈面上的点;ω为转子转速。
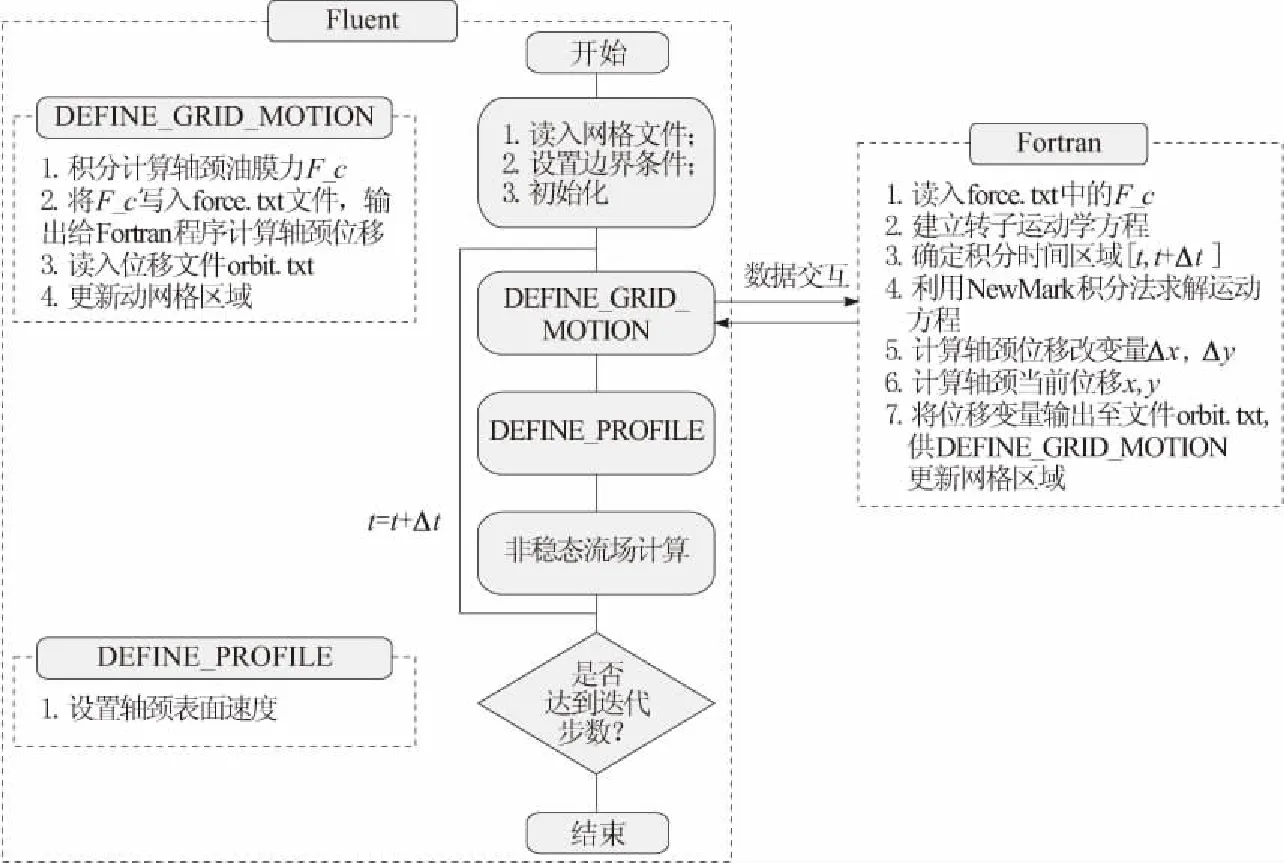
图2 滑动轴承流场固体耦合计算程序流程
滑动轴承流场计算的边界条件说明如图3所示。一般滑动轴承的润滑油由两端进油口流入油槽,油槽中的油流入轴承油膜,最终从轴承两端油膜间隙流出。因此,轴承进油口设置为压力边界条件,给定进口总压力;油膜间隙出口设置为压力边界条件,压力根据实际情况设定为环境大气压。轴颈面和轴承面均设置为固壁边界,其边界设置为无滑移条件,近壁面应用标准壁面函数。轴颈表面的旋转速度采用如前所述的DEFINE_PROFILE宏进行设定。
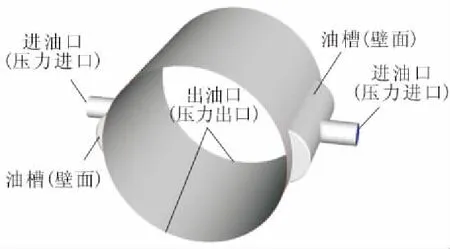
图3 滑动轴承流场计算边界条件
3 仿真结果及分析
椭圆弧面轴承与传统椭圆轴承的轴心轨迹对比如图4所示。由图4可知,转轴从坐标原点开始,在重力和油膜力的共同作用下,最终趋近于平衡位置。但是传统椭圆轴承的平衡位置偏高。一般对滑动轴承而言,平衡位置越低意味着轴承的稳定性越好,而平衡位置越高,甚至如图4所示高于水平线(Y=0 μm),意味着稳定性较差。由此可知,椭圆弧面轴承的稳定性比传统轴承要好。
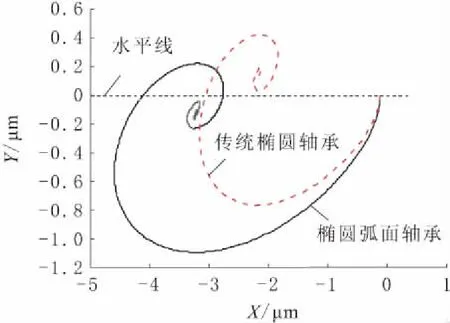
图4 轴心轨迹对比
椭圆弧面轴承与传统椭圆轴承的平衡位置点的压力分布对比如图5所示。可以看到,与一般圆轴承相比,椭圆轴承在工作中形成了2个收敛区和发散区,在轴颈上移时,上轴瓦很明显地形成了收敛油楔,能有效抑制轴颈的涡动。而一般来说,圆柱轴承的上半瓦依然是发散油楔,大部分被空穴覆盖,即轴颈向上运动时,上轴瓦几乎不起作用,因此在轴颈高速运行时容易失稳。
结合表1给出的油膜承载力和最大油膜压力,可见2种情况下的油膜承载力相差较小,与转子重量保持一致,这也说明了计算结果的准确性。而由于椭圆弧面轴承的平衡位置偏低,因此,在下轴瓦上形成的最大油膜压力也就比传统轴承要高,这与前文轴心轨迹的对比结果相一致。
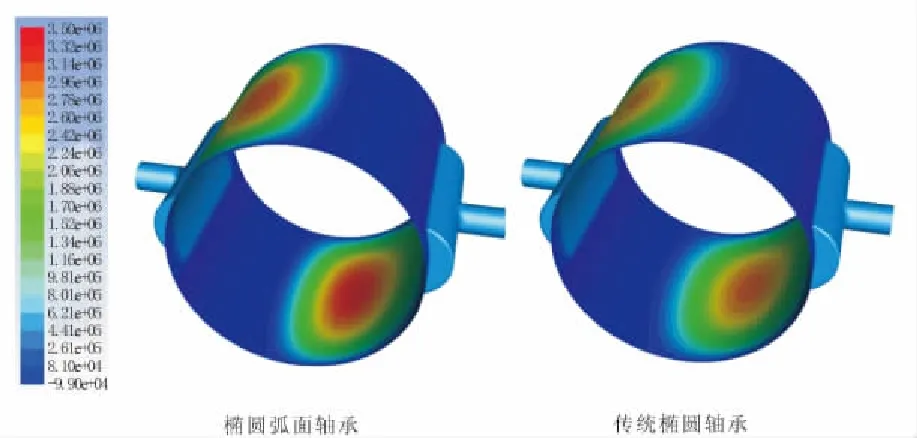
图5 压力分布对比

表1 承载力和最大油膜压力
4 结束语
本文提出一种针对椭圆弧面轴承的变流域结构化动网格方法,保证椭圆弧面轴承中油膜间隙网格随着轴颈的动态移动而规律性变化,在此基础上建立形成多流域-转子动力学方程耦合,计算得到轴心轨迹、压力分布等参数,并与传统椭圆轴承进行了对比。结果表明,椭圆弧面轴承轴心轨迹及压力分布与一般滑动轴承特性一致,且椭圆弧面轴承的平衡位置偏低,最大油膜压力偏大,稳定性比传统轴承要好,这与一般椭圆弧面轴承性能优于圆轴承的认识相符合。

