管壳式换热器的数值模拟和管束支撑分析

,，

(1．西安工程大学机电工程学院,陕西 西安 710048；2.北京化工大学机电工程学院，北京 100029)

0 引言

固定管板式换热器广泛应用于石油、化工等行业，由压力及温差载荷引起的壳体或换热管轴向应力往往对管束或壳体失效起控制作用[1]。因此，对固定管板式换热器进行设计时，往往考核换热管及筒体中的轴向应力以及管板弯曲变形。

姚琳[2]、刘天丰[3]、章姚辉[4]和陈楠等[5]应用实体单元、壳单元和梁单元建立了换热器有限元模型，详细分析和对比了换热器模型的管板应力、变形以及换热管轴向力，以探寻较为合理的管板结构数值分析模型。于洪杰等[6]认为，换热管实际支撑作用较管板设计计算中所考虑的管子支撑作用大。肖丽华[7]计算得到壳体最高点的主应力值小于无换热管加强时的主应力值，证明了管束对壳体具有加强作用。桑如苞[8]提出换热器壳体与管板及换热管组成的管板系统由于变形协调产生的边界力会引起壳体的轴向应力，并且管束刚度与壳体刚度相当时，由于双方的轴向刚度都较大，会在壳体和管束中引起较大的轴向力。

本文将建立不同单元类型的换热器有限元模型，通过对比换热器筒体和管子中的轴向应力以及管板挠度，分析不同换热器有限元分析方法的合理性；另外，以换热器壳体轴向应力为指标，考察换热管对换热器管板的支撑作用。

1 换热器有限元模型的建立

1.1 换热器几何模型和网格模型

所建换热器几何模型包括管板、部分长度筒体及换热管，如图1所示，其主要参数如表1所示。

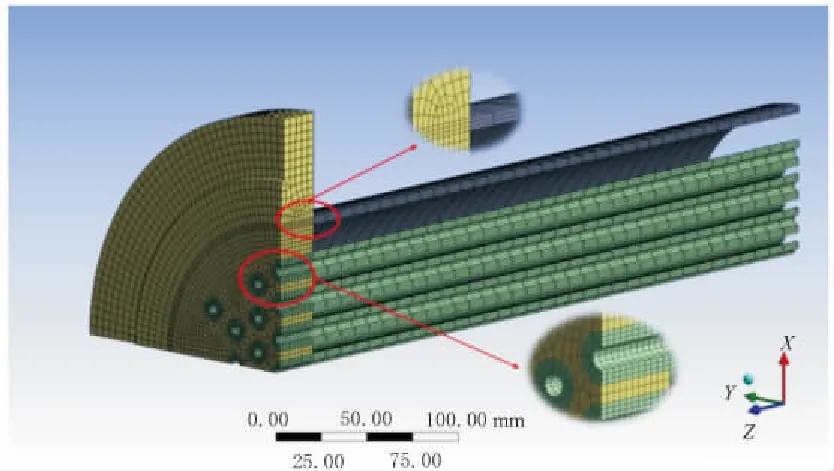
图1 换热器3层实体单元换热器网格模型

表1 换热器模型的主要参数

采用ANSYS17.0软件建立管板有限元模型，为了提高计算效率，同时不改变所研究问题的本质，这里利用结构对称性建立1/4结构换热器模型。

换热器是个特殊的结构，管子和筒体壁厚薄，而管板厚度大。就网格划分来说，管板应采用实体单元，管子和筒体既可采用实体单元，也可采用实体壳单元，如不作疲劳分析，还可采用壳单元。实体单元和实体壳单元或壳单元间采用MPC连接。

本文拟采用不同单元类型进行网格划分，得到4种不同的换热器模型，进行应力分析并对结果进行比较。这4种换热器模型是：管板采用实体单元(SOLID185)，管子和壳体均采用实体单元，并沿壁厚都划分3层；管板采用实体单元，管子和壳体均采用实体单元，沿壁厚只划分1层；管板采用实体单元，管子和壳体均采用实体壳单元(SOLSH190)；管板采用实体单元，管子和壳体均采用壳单元(SHELL181)。

1.2 载荷与边界条件

有限元模型的载荷与边界条件设置如下：

a.在管板壳程侧、筒体内表面和换热管外表面施加0.937 MPa的压力。

b.以管板厚度方向为轴向，约束换热管以及筒体最外侧端面的轴向位移。

c.在对称截面上施加对称约束。

1.3 应力分析结果及比较

对于中低压管壳式换热器，壳体、管子轴向应力和管板横向变形是主要考核指标，下面就对3个指标提取分析结果并进行比较。

对于实体单元和实体壳单元，沿壳壁厚度进行应力线性化，可得膜(平均)轴向应力和膜+弯轴向应力；对于壳单元，软件可直接给出膜及膜+弯轴向应力。

在不同换热器模型的筒体中部(远离管板)同一位置提取的轴向应力如表2所示。

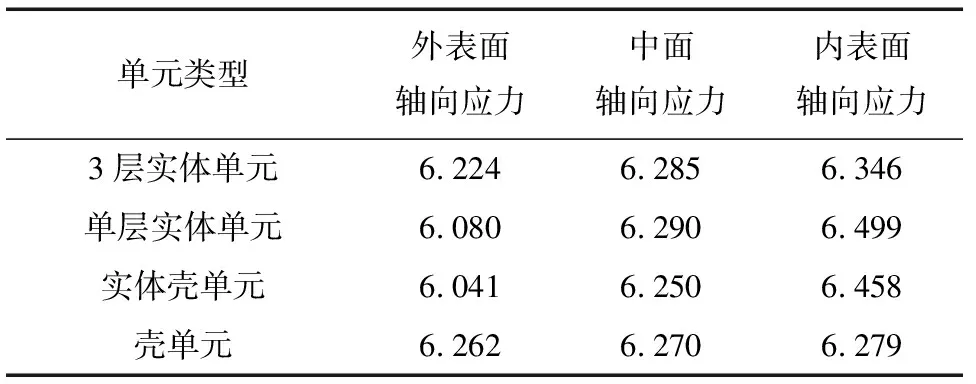
表2 筒体中部轴向应力分析结果 MPa

由表2可知，换热管与筒体无论采用实体单元、实体壳单元还是壳单元，无论是在筒体内表面，还是外表面或中面，筒体上的轴向应力没有明显区别，应力数值误差小于4%，其中平均轴向应力(中面应力)相差更小。从管板附近开始沿筒体轴向提取的平均轴向应力如图2所示。可以看出，各模型得到的结果差别都很小。对于轴向应力，采用3层或单层实体单元划分，结果没有明显差别。另外还可以看出，在管板附近，由于存在不连续应力，应力变化较大。

从管板附近沿换热管轴向提取的管子平均轴向应力如图3所示。可以看出，对于换热管，不同模型所得到的结果相差也不大，最大和最小相差在8%之内。同样，对于管子轴向应力，采用3层或单层实体单元划分网格所得结果几乎一样。

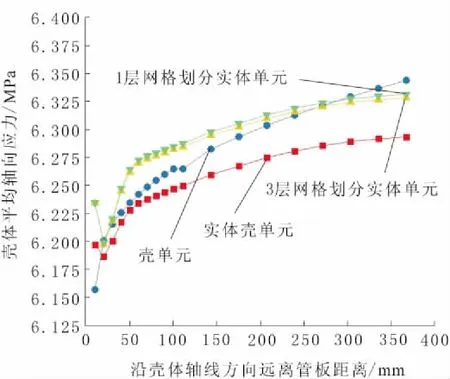
图2 筒体平均轴向应力随离开管板距离的变化

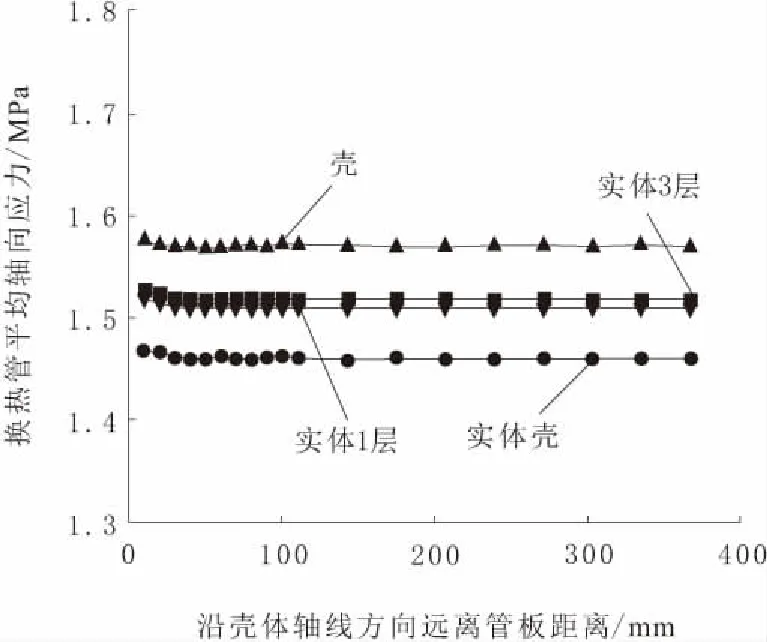
图3 换热管平均轴向应力随离开管板距离的变化

采用实体壳模型得到的管板挠度变化云图如图4所示。表3列出了不同单元类型的换热器模型中管板中心附近同一点的挠度，可以看出，各模型得到的挠度相差很小。

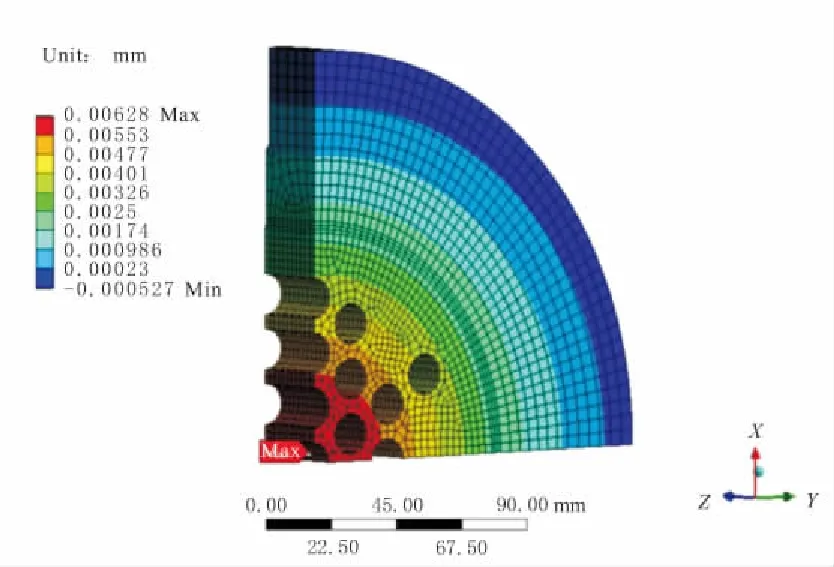
图4 管板挠度变化云图

表3 不同单元类型下管板挠度结果mm

综合前面的结果可以看出，对于薄壁管壳式换热器，进行有限元分析时，如需要进行疲劳分析，壳体和管子可以采用实体壳单元，而无需进行疲劳分析时，壳体和管子还可以采用壳单元划分。这一点有较大工程应用价值，因为对于大型管壳式换热器，这样数值模拟可以显著降低建模难度，减少计算时间。

2 换热器管束支撑分析

在管壳式换热器中，管子对管板有支撑作用，本节将以筒体中的轴向应力为指标，分析不同数量管子的支撑作用大小。本节将采用前面的实体单元模型进行分析，载荷和边界条件同前面一样。

为考察换热管根数对换热器管板的支撑作用，建立多个数目换热管的换热器模型。表4列出了换热器筒体中部的应力分析结果，显然，管子根数对筒体环向应力没有影响，而对轴向应力影响较大，管子越多，轴向应力越小，这是可以理解的，因为管子越多，换热器轴向承载面积越大。

换热器轴向应力分布云图如图5所示。可以看出，筒体所受轴向应力明显大于换热管所受轴向应力，因管板各处变形(挠度)不同，各个换热管所受轴向应力也不尽相同。

图5 换热器轴向应力分布云图

为比较起见，这里对筒体中环向和轴向应力进行以下简单理论计算[9]:

(1)

(2)

σz为筒体轴向应力；σθ为筒体环向应力；P为壳程压力；Di为筒体内径；t为筒体厚度；S为管板壳程承压面积；Ss为筒体金属截面面积；St为管子金属截面面积。

结果发现，按式(1)计算的筒体环向应力大小和表2中的有限元结果非常接近；在没有换热管时，按式(2)计算的筒体轴向应力值和有限元计算结果一致，但有换热管时，轴向应力的有限元计算值大于公式计算值，而且管子根数越多，相差越大，如表5和图6所示。

表5 筒体轴向应力随换热管根数的变化

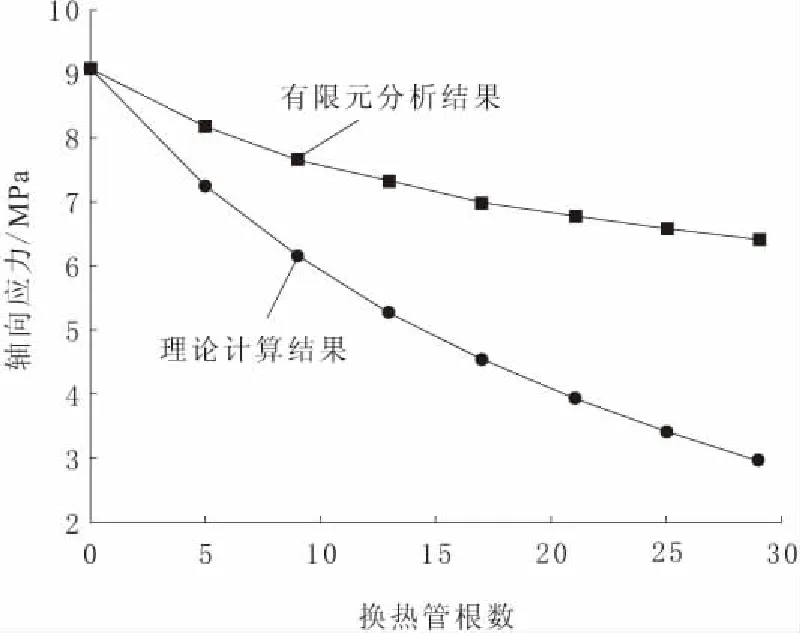
图6 筒体轴向应力随换热管根数的变化

进一步分析发现，管板横向变形(挠度)和换热管外侧及筒体内侧施加了壳程压力,是导致公式计算和有限元计算结果相差很大的原因。管板变形使得管子受力和筒体受力不一样；当换热管外侧受壳程压力作用时，由于泊松比效应，换热管伸长，结果对管板造成了支撑力减小甚至是附加推力，使得筒体轴向应力增大；筒体径向变形也会引起轴向应力变化。计算表明，若管板刚度足够大，管板不发生变形，则换热管所受轴向应力分布均匀，并且如果有限元分析时仅对管板进行加载，则筒体所受轴向应力与换热管所受轴向应力几乎相同，并且与式(2)计算结果相接近。所以影响换热器筒体中轴向应力的因素较多，也比较复杂，其精确计算最好采用有限元法，而以轴向力除以轴向承载面积的计算结果误差较大，对于本文的载荷，式(2)计算结果偏小，由此可知设计偏于冒进。

3 结束语

对于中低压管壳式换热器，换热管与筒体的网格划分无论采用实体单元、实体壳单元还是壳单元，筒体和管子上的应力计算结果差别都不大，轴向应力数值相差小于4%，管板挠度数值相差小于3%。所以，对于大型管壳式换热器，在需要进行疲劳分析时，可采用实体壳单元划分筒体和管子网格，而无需进行疲劳分析时，则可以采用壳单元，以显著降低建模难度，减少计算时间。

换热管数目对换热器筒体中的环向应力没有影响，但对轴向应力的影响明显，对于本文的壳程加载，换热器模型中换热管数目越少，换热器筒体所受轴向应力越大。

管板横向变形和换热管外侧及筒体内侧施加的壳程压力也都影响筒体中的轴向应力，采用有限元法是轴向应力精确计算的有限方法，如果简单地将轴向力除以轴向承载面积，其计算误差较大，对于本文情况，此设计偏于冒进。