存在同轴度误差的径向永磁联轴器传动特性分析*
田 杰,赵晓聪
(合肥工业大学 机械工程学院,安徽 合肥 230000)
0 引 言
随着铷铁硼永磁材料的广泛应用,永磁联轴器在近些年来得到了空前的发展,永磁联轴器具有对动力源隔离振动、过载保护、能够实现软起动、装配维修拆卸方便等优点,现已广泛应用到矿山机械、风力传动以及危险介质传动等场合[1]。
由于其在工程应用中具有非常好的应用前景,国内外关于永磁联轴器的研究在近年来也在不断推进,国外对于永磁联轴器的理论研究体系比较完善,从结构设计到参数优化,从仿真分析到实验探索都已经形成一套比较系统的研究体系[2-4];国内由于研究起步较晚,目前对于永磁联轴器的研究主要集中在磁场分布、结构优化、机械特性的计算[5-7],而对于永磁联轴器在实际工程应用由于制造或安装误差带来的传动不平稳问题国内外还没有系统的理论和方法来进行研究和分析。
径向永磁联轴器结构示意如图1所示。

图1 同步式径向永磁联轴器结构示意图1.主动轴 2.内转子 3.永磁体 4.永磁体 5.外转子 6.从动轴
其主从动转子上的永磁体采用轴向充磁,主动转子随着主动轴旋转时,永磁体间产生相对转角,从动转子受到磁力作用带动输出轴转动。由于径向永磁联轴器主从动转子不接触,在制造和安装过程中径向永磁联轴器主从动转子间易产生一定的不对中误差,从而引起传动不平稳、效率降低、轴心大幅度振动等问题,甚至导致结构的破坏[8]。因此,研究此类永磁联轴器同轴度误差下的转矩特性对于径向永磁联轴器系统的安装调整、结构优化、参数设定等方面具有重要的实用价值。
1 磁场分析
研究同轴度误差对径向永磁联轴器转矩特性的影响,首先需要对存在误差的系统进行磁场分析,研究误差对磁场分布的影响以此初步分析系统是否满足传动要求。由于径向永磁联轴器结构的对称性,可以采取轴心截面进行二维磁场分析。
根据参考文献[9],取径向联轴器两磁环的材料参数和几何尺寸如表1所列。以外磁环轴线为中心,将内磁环沿竖直方向偏移,设置同轴度误差分别为0 mm、1 mm、3 mm、5 mm。

表1 磁环材料参数及尺寸参数
在Ansoft Maxwell 2D中构建二维模型,根据磁极的矫顽力和剩磁参数设置永磁材料,将外部空气设置为Vector Potential边界。采用基于模型内部单元边长进行模型网格划分,长度设置为1 mm。设置求解器后启动求解。根据仿真结果可得二维磁场分布如图2所示。
根据图2中分析结果可看出,当同轴度误差为0 mm时,磁力线和磁场强度都是对称分布,径向永磁联轴器正常运转;随着同轴度误差的逐渐增大,系统磁场分布逐渐出现不对称不均匀的现象,导致系统出现传动不稳定的情况;当同轴度误差达到5 mm时,从磁场分布图2(d)中可以看到磁力线出现明显的疏密区别,上、下部分磁力线密度数值出现较大偏差,联轴器系统无法保证正常传动,故安装和制造过程中的同轴度误差对系统稳定传动会产生很大的影响,需要对其进行进一步定量分析计算。

图2 不同同轴度误差下的磁场分布图
2 传递转矩理论计算
磁荷库伦定律作为等效磁荷计算法的核心理论,其基本思想是计算空间内两微小固定点磁荷之间的作用力。对于径向永磁联轴器而言,将联轴器内的永磁体磁化表面等效为若干个磁荷微单元,进而得出两任意位置永磁体之间的磁力[10]。故同轴度误差下径向永磁联轴器结构可简化得以下计算模型,并以外磁环轴线方向建立x轴,以竖直方向建立z轴,构建笛卡尔空间直角坐标系Oxyz,如图3所示,假定内外两个永磁体磁环轴线相互平行无角度偏移且磁化方向相同。

图3 转矩计算模型
记M点是内磁环磁极表面1上任意点,则点M处的微元磁荷可表述为:
qm=σ1r1dr1dα
同理外磁环磁极表面3上任意点N微元磁荷可表述为:
qn=σ2r2dr2dβ
式中:r1为内磁环磁极表面任意点极长;r2为外磁环磁极表面任意点极长;σ1、σ2分别为内外磁环磁极表面的磁荷面密。
根据磁极化强度与磁荷面密度之间的关系式σ=Br·n(n为磁极表面的法线方向),当磁极化强度垂直于磁体表面时:
σ1=σ2=Br
基于磁荷库伦定律在同轴磁环内的推导公式,则两磁环的相应磁极表面1和3上任意两点之间的微元磁力为:
(1)
其中1、3磁极表面两微元磁荷的向量模长|r31|为:
式中:l为磁环轴向长度;Δx为轴向误差,Δy、Δz为径向误差(假定三个误差值分别沿坐标轴正向);r31为1、3面任意两点之间的空间向量;r1为内磁环的内径;r2为内磁环的外径;r3为外磁环的内径;r4为外磁环的外径。
微元磁力分解到三个坐标轴的分力为:
(2)
(r1sinα+Δy-r2sinβ)
(3)
(4)
同理可以得到联轴器其余磁极面之间的向量关系,将向量投影到各坐标轴长度如表2所列。
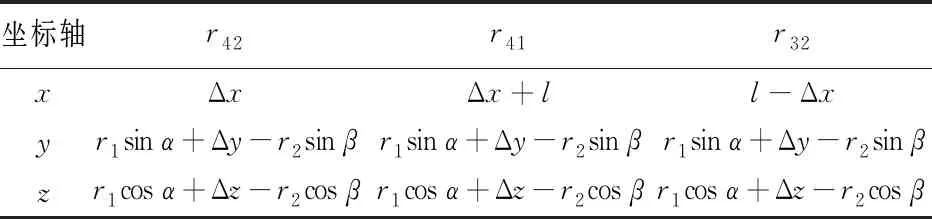
表2 其他向量在各坐标轴投影长度
表中r42表示4、2磁极表面两微元磁荷的向量模长;r41表示4、1磁极表面两微元磁荷的向量模长;r32表示3、2磁极表面两微元磁荷的向量模长。
磁力联轴器的传递转矩为各微元分力对x轴的转矩,如下表达式所示:
dT31x=dF31y(Δz+r1cosα)
+dF31z(r1sinα+Δy)
(5)
dT32x=dF32y(Δz+r1cosα)
研究组患者治疗后经胃镜检查结果痊愈率为88.33%,与对照组(68.33%)比较,研究组治愈率高于对照组,组间比较,差异具有统计学意义(P<0.05),详情见表2 。
+dF32z(r1sinα+Δy)
(6)
dT41x=dF41y(Δz+r1cosα)
+dF41z(r1sinα+Δy)
(7)
故联轴器系统对x轴的磁力转矩为:
dTx=dT31x+dT42x+dT41x+dT32x
[(r2sinβ-r1sinα-Δy)(Δz+r1cosα)+
(Δz+r1cosα-r2cosβ)(Δy+r1sinα)]×
r1r2dr1dr2dαdβ
(8)
对公式(8)积分可得到内外磁环之间磁力矩为:
[(r2sinβ-r1sinα-Δy)(Δz+r1cosα)+
(Δz+r1cosα-r2cosβ)(Δy+r1sinα)]×
r1r2dr1dr2dαdβ
(9)
3 转矩公式的仿真验证
公式(9)即为径向永磁联轴器在同轴度误差下的传递转矩计算公式。为验证公式正确性,利用Ansoft Maxwell仿真得出不同误差值下的传递转矩数值,与利用Matlab求解公式(9)所得传递转矩数值进行比对。
利用表1中数据建立不同安装误差下径向永磁联轴器三维模型,在Ansoft Maxwell 3D中构建三维模型,根据表1中矫顽力和剩磁参数设置永磁材料,将外部空气设置为Zero Tangential H Field边界。采用软件自带的自适应网格划分。设置力矩求解器后启动求解。
最后进行三维瞬态磁场分析计算,得出联轴器工作过程中的稳定传动转矩,将相同误差下磁场仿真值并与公式计算值进行对比,如表3所列。
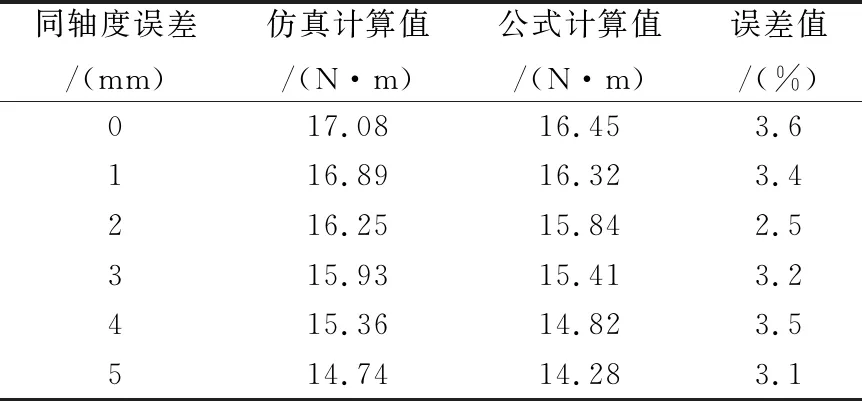
表3 转矩公式仿真验证对照表
从表3验证计算结果可以看出,公式计算结果与仿真值的误差保持在5%以内,证明所推导的公式具有很高的可行性,能够相对准确快速地计算出径向永磁联轴器存在安装误差下的传递转矩,可以为径向永磁联轴器的误差分析提供可靠的理论依据。
4 存在同轴度误差时转矩特性分析
传递转矩是径向永磁联轴器传动特性的关键衡量参数,通常在设计时通过改变表1所示的径向永磁联轴器的永磁体厚度,或调节主从动转子间径向气隙实现工作所要求的传递转矩,本节针对不同结构参数研究同轴度误差对传递转矩的影响,从而得出为保证各参数尺寸的联轴器系统可实现正常传动时的安装精度。
4.1 不同永磁体厚度下同轴度误差对传递转矩影响
永磁体径向厚度增加时其储存的磁能会增加,径向永磁联轴器的传动性能进一步提高,但会导致其制造成本的升高。因此一般在设计过程中遵循满足传动要求的最低成本化要求。保持联轴器系统其他结构参数不变,同时改变内转子的内径及外转子外径获得不同的内、外转子厚度。利用公式(9)计算得出各同轴度误差下永磁体厚度变化量为Δ时所对应的传递转矩,所得数据见表4所列,并利用Matlab作出相应的变化曲线如图4所示。

表4 同轴度误差下联轴器在磁体厚度变化下传递转矩 /N·m
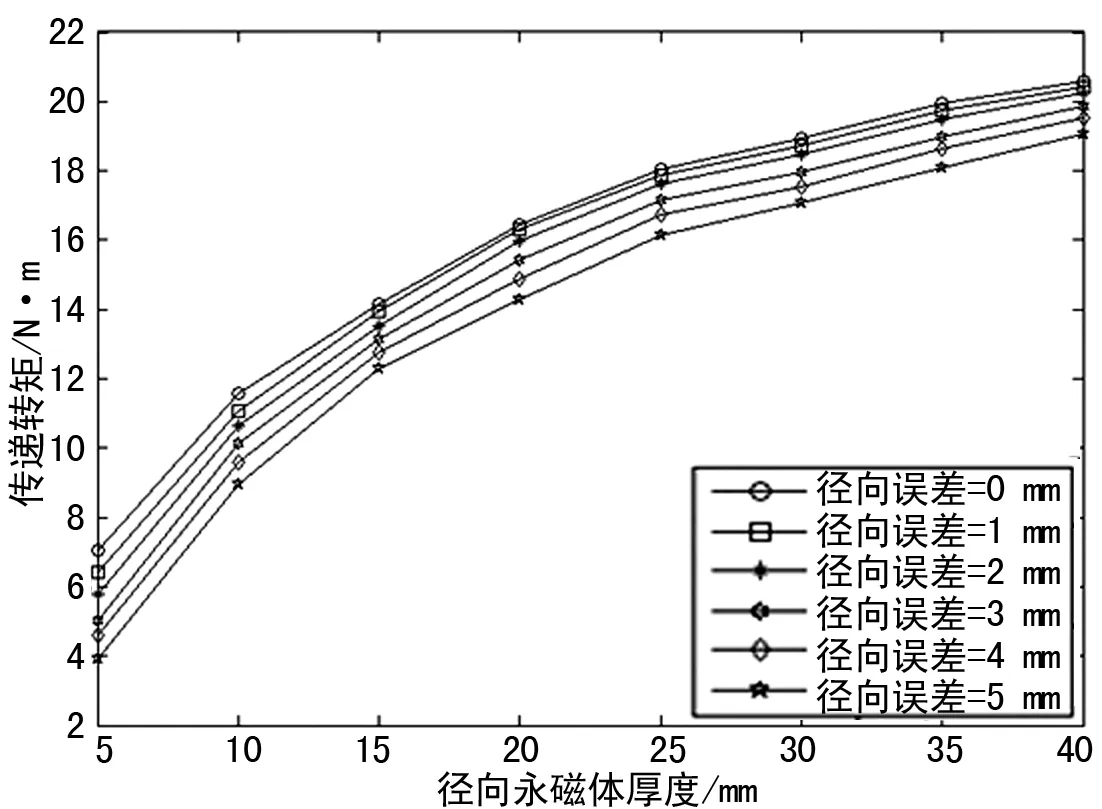
图4 不同磁体厚度下同轴度误差与传递转矩关系
从表4中数据和图4的变化趋势可以看出:随着永磁体径向厚度的增加,永磁体之间的作用力逐渐变大,即永磁联轴器的传递转矩越大,同轴度误差对联轴器系统的传递特性影响会逐渐降低。为了保证径向永磁联轴器传动的稳定性和高效性,即保证径向永磁联轴器在实际工作时的传递转矩可以达到原本设计时传递转矩的90%,进而推荐永磁体厚度尺寸为10 mm以下的径向永磁联轴器同轴度误差应保证在1 mm以内;同理,永磁体厚度为10~20 mm的径向永磁联轴器同轴度误差应保证在2 mm以内,永磁体厚度超过20 mm的径向永磁联轴器同轴度误差应保证在3 mm以内。
4.2 不同径向气隙下同轴度误差对传递转矩的影响
气隙是指在内外磁环之间的径向空气间隙,本节在分析不同气隙下同轴度误差对传递转矩影响时,通过将内永磁体磁环固定,改变外磁环尺寸达到改变径向气隙的大小。整个分析过程中外磁环尺寸增大会导致永磁体体积也进一步增大,所储存的磁能也进一步增大,过程中存在气隙和永磁体体积两个变量从而具有一定的局限性,相关计算分析对安装精度标准化有着相当可观的参考价值。计算得出各同轴度误差下内外磁环气隙变化量为Δ时所对应的传递转矩,所得转矩数据见表5所列,作出相应的变化曲线如图5所示。
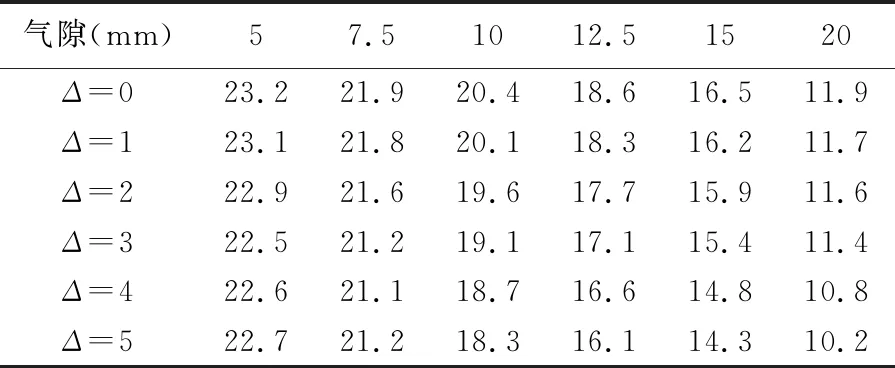
表5 同轴度误差下联轴器在气隙变化下的传递转矩 /N·m

图5 不同磁环气隙下同轴度误差与传递转矩关系
从表5中数据和图5的变化趋势可以看出:随着径向气隙的增大,径向永磁联轴器的传递转矩会逐渐降低;当内外磁环径向气隙较小时,同轴度误差对系统传递转矩的影响较小,但工作过程中当存在较大误差时较小的径向间隙很可能会导致主从动转子在产生振动的过程中发生碰撞;当内外磁环径向气隙逐渐增大时,同轴度误差对系统传递转矩影响逐渐增大。为了保证系统传动的稳定性和安全性,进而推荐内外磁环径向间隙为10 mm以下的径向永磁联轴器同轴度误差应保证在1 mm以内;同理,内外磁环径向间隙为10~15 mm范围的径向永磁联轴器同轴度误差应保证在2 mm以内,内外磁环径向间隙超过15 mm的径向永磁联轴器同轴度误差应保证在3 mm以内。
5 结 论
(1) 利用磁荷库伦定律推导得出同轴度误差下的径向永磁联轴器转矩计算公式,并通过数值计算和仿真验证对比验证了其正确性,从而可以应用到径向永磁联轴器的产品设计和同轴度误差标准化过程中。为径向永磁联轴器系统的安装调整、结构优化提供理论依据。
(2) 针对目前应用最为广泛的两类径向永磁联轴器,即永磁体厚度变化系列和径向气隙变化系列,利用公式计算得到联轴器正常传动所必须保证的同轴度安装精度,整个计算过程利用Matlab编程简单且准确率较高。
(3) 从磁场分析结果着手,利用等效磁荷法建立数学模型进行转矩计算的研究方法,可应用到其他类型磁力联轴器的结构设计和安装精度标准化过程。

