海洋环境下浮动堆设备闸门密封性能分析

(武汉第二船舶设计研究所，武汉 430064)

0 引言

在核电站事故工况下，设备闸门与安全壳一起形成第三层屏蔽，包容放射性物质，是安全壳压力边界的重要组成部分，也是安全壳压力边界较薄弱的环节[1-3];同时，浮动堆在海洋环境下会产生随机运动，压力载荷由外压转变为内压，因此，对设备闸门的密封性设计提出更为严苛的要求。

杜坤等[1]基于ANSYS有限元分析方案和国RCC-M《压水堆核电厂机械设备设计和建造规则》的理论，对核电厂设备闸门及支架部分进行了计算分析。左树春[4]基于ANSYS有限元分析研究了安全壳强迫位移造成的法兰面分离及相对错动，采用非线性接触分析，讨论了在事故工况压力作用下，法兰面的分离和相对位移。现有的研究简要分析密封性能变化，缺少对设备闸门密封面变形后O形圈密封性能定量计算分析。

本文结合水动力学和瞬态动力学，建立设备闸门三维模型，分析事故工况下设备闸门球面盖及下法兰的变形，提取最大变形处相对位移值；而后构建二维密封面模型，并基于二参数的Mooney-Rivlin本构模型，描述密封圈材料的应变能函数构建事故工况下密封面二维轴对称模型，模拟事故工况下密封面变形情况，分析密封圈总体变形、应力分布、接触应力分布，以判定海洋环境下浮动堆设备闸门事故工况下密封性能。

1 结构变形分析

核动力船舶与陆上核电站设备闸门结构分析的关键在于摇摆载荷与冲击载荷的确定，其余载荷可参照陆上核电设备闸门执行。

1.1 设计载荷

1.1.1 摇摆载荷

平台由船体和软刚臂单点系泊装置两部分组成。船体的运动与软刚臂的系泊回复力之间双向耦合，从而决定了平台为多体耦合模型，如图1所示。

图1 海洋核动力平台有限元模型

综合考虑海洋环境条件对船体的激励作用，以及由软刚臂提供的系泊回复力，船体时域运动方程[5]为：

=Fw(t)+Fwd(t)+Fc(t)+Fm(t)

(1)

式中m——船体的质量矩阵；

A(∞)——波浪频率无穷大时船体的附加质量矩阵；

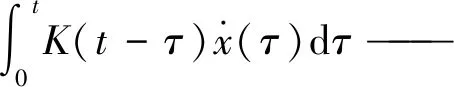
K(t)——时延函数；

C——船体的静水回复力矩阵；

Fw(t)——波浪载荷；

Fwd(t)——风载荷；

Fc(t)——流载荷；

Fm(t)——系泊回复力。

在考虑船舶摇摆对换料盖的影响时，假设换料盖为一质点，摇摆的中心位于水线面、船舶中心线与船舯的交点处。将其运动函数简化为角位移函数：

(2)

(3)

换料盖质心与水线面的垂直距离z=12.8 m，距离船舶中心线的水平距离x=5.55 m，距离船舯的纵向距离y=4.85 m，如图2所示。

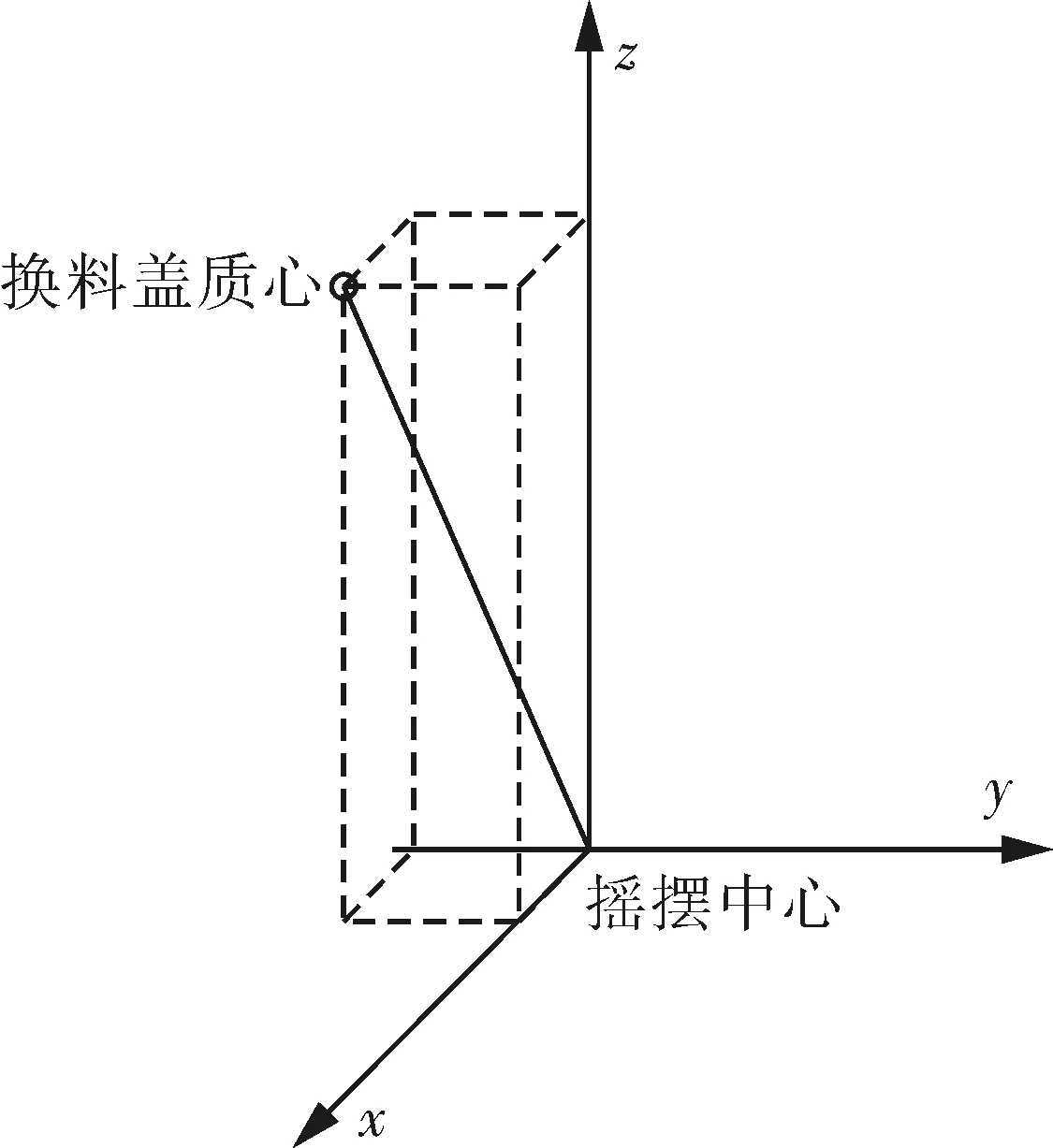
图2 换料盖相对于摇摆中心位置示意

横纵摇周期为5 s时，将横摇工况下换料盖的角位移函数转换为标准坐标系下的位移函数。将此位移函数作为位移载荷施加在换料盖下法兰底部，模拟正常工况下的纵横摇载荷。

1.1.2 冲击载荷

根据《浮动核动力装置设计中所选择的外部事件(试行)》中对船舶碰撞、爆炸等外部事件的要求，采用等效静力的方法确定设备闸门在设计工况下的冲击载荷为横向、纵向和垂向冲击谱加速度峰值均为4.5g，2.5g，1.5g，且在瞬态计算过程中考虑1.1倍的放大系数(动态系数)[6]。

1.1.3 其他载荷

在设备闸门球面盖板内侧面和法兰内侧面施加0.6 MPa的内压。结构自重G(包括附件重量)以惯性力的方式施加在整个模型上，为9 810 mm/s2。根据实际计算得到的螺栓数目确定螺栓的预紧载荷，施加在螺栓上。单个螺栓预紧力为110 kN[7]。

1.2 密封面变形分析

由于设备闸门整体受非对称载荷，选取变形量最大截面进行分析，如图3所示。在球面盖取1,2两点，下法兰取3，4两点，具体结果如表1所示。

图3 位移结果提取位置示意

表1 设备闸门球面盖及下法兰位移提取结果表

在图3中，可见提取的4个点的Y向位移的相对位移很小，可忽略不计，对上下法兰面的Z向位移，假设下法兰位置不变，转化为球面盖对下法兰的相对位移。

图3模型中，球面盖与下法兰初始间隙为4 mm，在事故状态下最终球面盖与下法兰两端的分离量分别为0.137，0.233 mm，其密封面在一定角度呈开口状分离。由此确定密封结构有限元模型中，下法兰施加固定约束，球面盖上法兰1，2两个端点的位移约束分别为3.863，3.767 mm，方向为贴合下法兰面方向，水平方向对球面盖和下法兰施加固定约束。

2 密封性能分析

2.1 密封判定准则

在密封性分析中，目前通用的O形密封圈密封性判定准则[8]是最大接触压应力大于工作压力的m倍则判定为密封，该m值即为垫片系数。本文密封圈采用三元乙丙橡胶，参考ASME第Ⅲ卷NE分册[9]要求，垫片系数m可取为1。因此，定义接触压应力大于0.6 MPa的密封接触面宽度为有效密封宽度。

参考文献[8]中压缩量试验，对其试验满足泄漏率要求的临界密封压缩量值，通过有限元建模计算，得到对应的有效密封宽度为3 mm，本文暂定设备闸门密封结构有限元计算结果中，有效密封宽度为3 mm时，也能满足许用泄漏率的要求。

通过有限元反复试算球面盖的上法兰施加向下位移量的大小，保证最大接触应力大于设计内压0.6 MPa，且留有至少3 mm的有效接触宽度，从而确定能保证密封的最小压缩量。

2.2 有限元分析

设备闸门密封圈材料选用三元乙丙橡胶(EPDM)，性能参数参照陆上核电站设备闸门相同材料的密封圈，泊松比μ=0.5，弹性模量E=7.84 MPa。

设备闸门球面盖和下法兰材料选用SA-738Gr.B级钢板。根据《D篇》[10]中表1A、表Y-1以及表TM-1可知，当温度为158 ℃时材料基本力学性能：材料许用应力S=168 MPa，材料屈服强度Sy=356 MPa，弹性模量E=192×103MPa。

2.2.1 理论模型

由于设备闸门密封结构是轴对称结构，故可简化为二维轴对称模型，如图4所示。

图4 设备闸门密封结构模型

在模型中，假设密封圈的泊松比为0.5，即不可压缩材料。上下法兰面的弹性模量是密封圈材料的几万倍，故假设上下法兰面为刚体，不考虑其变形。

密封圈属于超弹性材料，其力学模型表现出复杂的材料非线性和几何非线性，本文基于二参数的Mooney-Rivlin本构模型[11]描述密封圈材料的应变能函数，其函数表达式为：

W=C10(I1-3)+C01(I2-3)

(4)

式中W——应变能；

I1，I2——第一、第二Green应变不变量；

C01，C10—Mooney-Rivlin系数。

根据密封圈材料的硬度或弹性模量可计算两个参数的具体值，密封圈弹性模量E与两个参数的关系[12]如下：

(5)

对弹性模量为7.84 MPa的橡胶圈，得到C10=1.045 MPa，C01=0.261 MPa。

2.2.2 载荷及边界条件

模型中包含两个接触对：(1)上法兰与O形圈的接触；(2)下法兰与O形圈的接触。均为摩擦型非对称接触，摩擦系数为0.2，接触算法采用增强的拉格朗日乘子法[13]。事故状态下密封性分析的载荷及边界条件如表2所示。

表2 载荷施加情况

2.2.3 事故状态下密封性分析

密封结构的计算结果云图如图5～8所示。

图5 压缩率为5%时接触应力云图

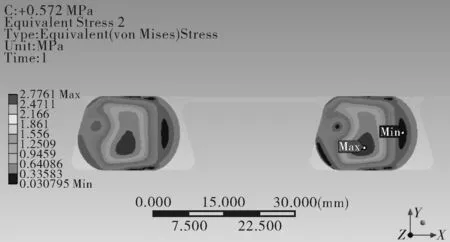
图6 密封结构应力云图

图7 密封圈接触应力云图

在施加载荷过程中，当压缩量为5%时，最大接触应力为0.962，有效密封宽度为3 mm，可认为已经达到有限密封。达到事故工况下的位移约束时，即两个端点的位移约束分别为3.863 mm和3.767 mm，压缩量为19.8%时，最大接触应力3.813 MPa，有效密封宽度为12 mm，且密封圈应力在材料性能范围内。

图8 有效密封宽度云图

3 结论

(1)本文通过结合水动力学和瞬态动力学，分析事故工况下设备闸门球面盖及下法兰的变形，并基于二参数的Mooney-Rivlin本构模型描述密封圈材料的应变能函数构建事故工况下密封面二维轴对称模型，分析密封圈总体变形、应力分布、接触应力分布，提出判定海洋环境下浮动堆设备闸门事故工况下密封性能的方法，可为实际工程提供参考。

(2)浮动堆安全壳由于空间限制，设备闸门安装在安全壳外部，事故工况下受内压，其密封面在一定角度呈开口状分离。密封圈压缩量由21%变为19%，密封面分离量达到0.233 mm，需要预压缩量为密封提供足够的余量。

(3)现有设计方案中，当压缩量为5%时，最大接触应力为0.962，有效密封宽度为3 mm，理论上可以保证密封，考虑到在实际工作中，密封圈受到加工、安装、密封面的加工精度等因素的影响，且密封结构需要在事故状态下依旧保持密封性能，结合以往工程经验，设密封圈预压缩率选取的安全系数为4，对预压缩量取整，得到密封圈的预压缩量为4 mm，预压缩量为21%。密封设计安全系数为4。