基于QD-SOA-XGM的全光逻辑或非门研究*

王玉倩，王海龙，孔雪纯，杨 帅，龚 谦

（1.山东省激光偏光与信息技术重点实验室 曲阜师范大学 物理系，山东 曲阜 273165；2.中国科学院 上海微系统与信息技术研究所 信息功能材料国家重点实验室，上海 200050）

0 引 言

全光网络系统作为光网络路由节点上信号电流光电转换的替代方案，引起了人们的广泛关注，其中对路由识别等信号的处理需要全光逻辑门器件。全光逻辑或非门（All-optical logic NOR gate，NOR）可以实现全光码型转换、传输误码检测、路由地址识别等信息处理功能[1]。全光逻辑处理系统在光通信的路由识别、全光码型转换等过程中都有重要用途[2]。半导体光放大器（Semiconductor Optical Amplifier，SOA）因其非线性、温度灵敏性好、体积小、重量轻、成本低、结构简单且易于集成等优点，成为研制全光逻辑器件材料的首选[3]。相对于SOA来说，量子点半导体光放大器（Quantum Dot Semiconductor Optical Amplifier，QD-SOA）具有更短的增益恢复时间，可以更高速地处理大量数据。

根据文献[4]可知，当输入信号光A和B中输入3个连“0”高斯脉冲时，量子点半导体光放大器的载流子浓度可以得到充分恢复，所以输出信号可以得到更高的增益，即峰值功率较高，定义为P30。然而，当输入信号光A和B中输入2个连“0”高斯脉冲时，量子点半导体光放大器的载流子浓度难以得到充分恢复，即输出信号难以得到较高的增益，即峰值功率较低，定义为P20。不同信号光对应输出波形峰值功率的比值P30/P20可以代表全光逻辑门仿真结果的码型效应特性。码型效应越小，P30/P20越小，即全光逻辑门性能越好。

本文研究了全光逻辑或非门的码型效应特性，基于级联结构的QD-SOA与单个SOA相比，能有效改善输出光信号的消光比，且也可以缓解码型效应的影响。

1 理论模型

1.1 QD-SOA的能级结构

QD-SOA与传统SOA的不同在于QD-SOA的有源区具有三维受限且按一定规律排列的量子点[5]。量子点的能级结构分为低能级基态（Ground State，GS，）、较高能态激发态（Excited State，ES）和浸润层（Wetting Layer，WL）[6-7]。电子跃迁时间能达到ps量级，使得QD-SOA的增益恢复时间也是ps量级。

如图1所示，如果注入电流载流子浓度足够高，电子会以跃迁时间τW2跃迁到ES，以跃迁时间τ21从ES向GS跃迁。此外，电子会以时间τWR从WL自发辐射，并以时间τ1R从GS自发辐射。另外，电子会从GS向ES和从ES向WL逆向跃迁，弛豫时间分别为τ12和τ1W。最后，输入光和GS电子得到受激辐射，输入光得到放大。

图1 QD-SOA能级结构

1.2 QD-SOA工作原理

假设QD-SOA是理想的双端QD-SOA，即模型忽略色散和ASE噪声，可以得到QD-SOA的光场传输方程[8-10]为：

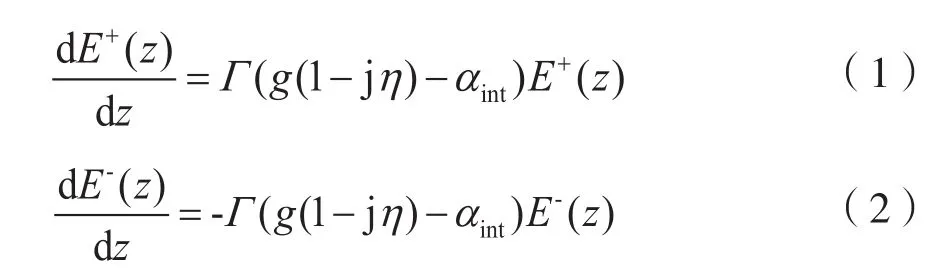
其中Z是光场的传输方向，E+是沿着正（反）方向传输的光场强度，而E-是沿着反方向传输的光场强度，Γ是光场的限制因子，j=(-1)1/2，η是限宽增强因子，αint是损耗系数。

上述方程的边界条件[10]为：

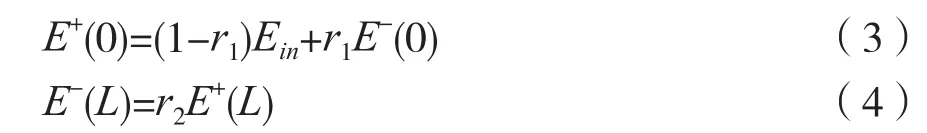
在QD-SOA中，载流子浓度分布变化、输出特性和增益特性采用三能级速率方程描述。该载流子跃迁速率方程[11-12]可以表示为：

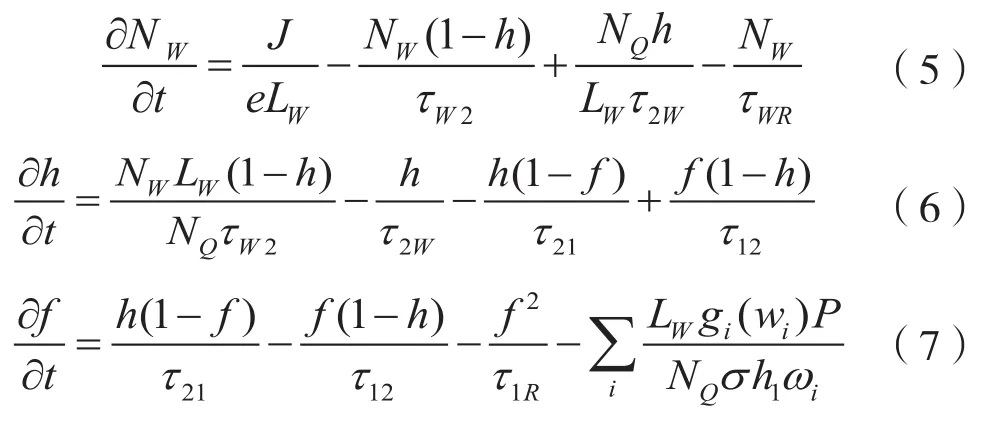
其中，NW为WL的电子浓度，J为注入电流密度，LW为有源区厚度，f和h分别为GS和ES中电子占有的概率，τW2为载流子从WL跃迁到ES跃迁时间，τ2W为电子从ES向WL弛豫时间，τWR和τ1R分别为WL和GS的自发辐射时间，NQ为量子点表面的密度，τ21为从ES跃迁到GS的跃迁时间，τ12为从GS向ES逆向跃迁的弛豫时间，gi为分段模型的第i段的模式增益，h1ωi为光子的能量，ωi为光波角频率。

采用分段模型[13-14]和四阶龙格-库塔法[15]求解上述方程。QD-SOA的有源区均被分为M段，第i段长为ΔL=L/M，第i段传输时间为Δt=ΔL/c，这样各段的载流子浓度分布可以近似认为是均匀分布的。

2 数值模拟

基于量子点半导体光放大器的交叉增益调制效应[16]的全光逻辑或非门结构图如图2所示。波长为λ1的连续光CW和波长为λ2的信号光A经耦合器耦合进入第一级QA-SOA。设置信号光A的峰值功率远大于连续光CW的峰值功率，则第一级QD-SOA的增益饱和效应主要由信号光A决定。当信号光A为数据“1”时，消耗QD-SOA1中的载流子，SOA1的载流子浓度降低。此时，无论连续光CW为“1”或“0”，输出为“0”。只有当信号光A为数据“0”时，CW才可以通过QD-SOA1得到放大，QD-SOA的输出为“1”，因此第一级SOA1的输出为A-。

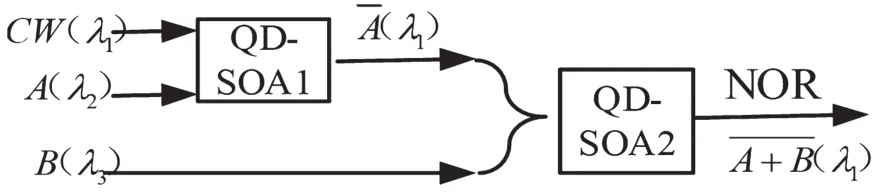
图2 QD-SOA-XGM型全光逻辑或非门结构

逻辑或非门的真值表，如表1所示。

表1 逻辑或非门的真值表

2.1 数值模拟结果

输入的两路信号是脉冲宽度为5 ps、速率为50 Gb/s的一阶高斯脉冲模拟信号[17]，注入电流为80 mA，输入信号数据A的峰值功率为10 dBm，连续光CW的峰值功率为0 dBm，输入信号光B的峰值功率为20 dBm，输入信号光A波长为1 550 nm，输入信号光B和连续光CW的波长为1 500 nm。

输出结果中，连续光的输出码型与输入信号光的码型相比，在时间上存在一个向后的延时[18]，这是因为量子点半导体光放大器载流子消耗速率迅速，但是恢复速率缓慢。所以，在实际模拟中，为了使第一级QD-SOA的输出与信号光B保持同步，需要将作为泵浦光的高斯脉冲B在时间上略微向前调整 0.5×20 ps。

要实现逻辑或非功能，需要满足信号光B的峰值功率远大于信号光A的峰值功率。不改变第一级QD-SOA1的参数，将A-的峰值功率衰减20倍[4]，同时设置信号光B的峰值功率为20 mW。信号的输入高斯脉冲序列为“110010001”，信号的输入高斯脉冲序列为“011001001”，所以输出信号的脉冲序列为“000100110”，最后可以模拟出逻辑或非的理论结果。模拟结果会出现码型失真，但可以通过调节参数的方法给予改善。

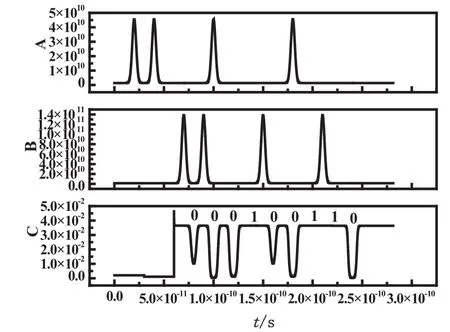
图3 QD-SOA-XGM-NOR仿真结果

2.2 输入光功率和P30/P20的关系

在其他参数不变的条件下，当两级半导体光放大器的注入电流分别为I1=80 mA、I2=90 mA，I1=80 mA、I2=100 mA和I1=90 mA、I2=100 mA三种情况时，P30/P20随P2-CW的变化，如图4所示。由图4可以看出，在一定取值范围内，第一级输入电流越小，P30/P20的值越小，逻辑或非门的性能越好。这是由于在一定范围内输入电流越小，第一级放大器的放大效果越差，输出的A-的值越小。而A-又作为第二级SOA的探测光，A-的值越小，第二级SOA的放大效果越好，或非门输出性能越好。此外，由图像可以看出，在一定取值范围内，输入连续光功率越大，P30/P20比值越小，或非门输出效果越好。这是因为连续光CW作为输入探测光，增大其峰值功率，会使有源区增益减小并迅速饱和产生非线性效应，从而加快增益恢复。

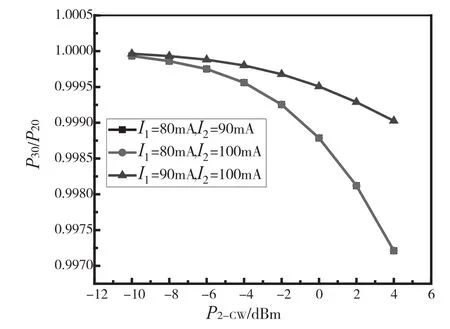
图4 连续光功率与P30/P20的关系

2.3 有源区长度和P30/P20的关系

在其他参数一定的情况下，当数据B的峰值功率分别为20 dBm、25 dBm、30 dBm时，随着有源区长度的增加，P30/P20的变化如图5所示。由图5可以看出，在一定取值范围内，有源区长度越长，P30/P20比值越小，或非门输出效果越好。当有源区长度从1.5 mm增加到2.0 mm时，P30/P20的值不断减小。这是因为有源区长度越长，累积的电流量越大，载流子数量越多，载流子也就越容易受激辐射，调制效果越好。但是，有源区长度一定时，改变峰值功率，或非门输出性能没有明显变化。

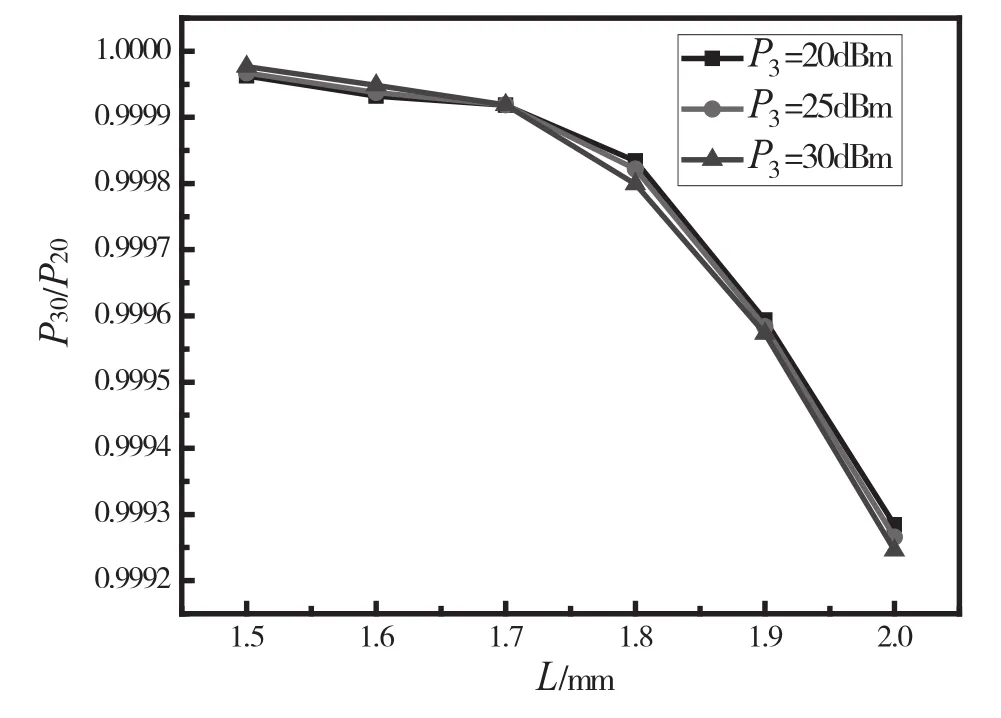
图5 有源区长度与P30/P20的关系

2.4 有源区宽度和P30/P20的关系

在其他参数一定的情况下，当数据B的峰值功率分别为20 dBm、25 dBm、30 dBm时，随着有源区宽度的增加，P30/P20的变化如图6所示。由图6可以看出，在一定取值范围内，有源区宽度越宽，P30/P20比值越小，或非门输出效果越好。当有源区宽度从2 μm增加到10 μm时，P30/P20的值不断减小。这是因为有源区宽度W越大，源源不断注入电流时累积的载流子数量越多，载流子也就越容易受激辐射，调制效果越好[19]。从图6可以看出，在一定取值范围内，或非门的性能随着输入光功率的增大而变好。这是因为输入光作为泵浦光，输入光功率越大，QD-SOA的放大效果越好，或非门输出性能越好。

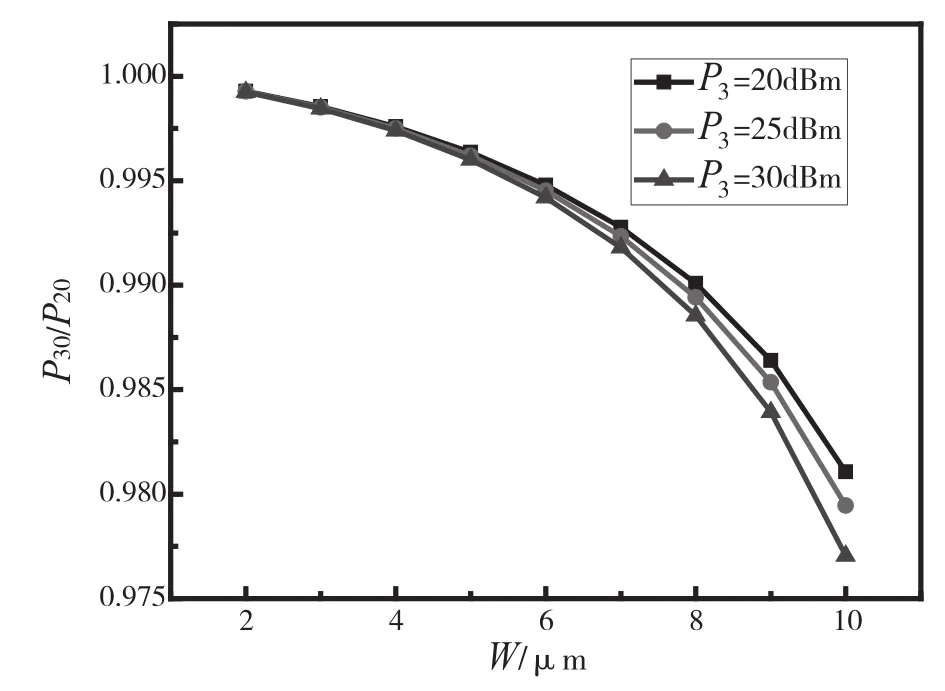
图6 有源区宽度与P30/P20的关系

2.5 最大模式增益和P30/P20的关系

在其他参数一定的情况下，当有源区长度分别为1.5 mm、1.8 mm、2 mm时，随着最大模式增益的增加，P30/P20的变化，如图7所示。由图7可以看出，在一定取值范围内，最大模式增益越大，P30/P20比值越小，或非门输出效果越好。当最大模式增益从1 200 m-1增加到3 000 m-1时，P30/P20的值不断减小。这是因为最大模式增益的增加，使得有源区内载流子的变化速率增快，最终导致载流子浓度的变化。从图7可以看出，当最大模式增益一定时，在一定取值范围内，或非门的性能随着有源区长度的增大而变好。当有源区长度从1.5 mm增加到2.0 mm时，P30/P20的值不断减小。这是因为有源区长度越大，载流子越容易受激辐射，泵浦光的调制效果也越好。

2.6 损耗系数和P30/P20的关系

在其他参数一定的情况下，随着损耗系数的增加，P30/P20的变化如图8所示。由图8可以看出，在一定取值范围内，损耗系数越大，P30/P20比值越大，或非门输出效果越差。当损耗系数从140 m-1增加到320 m-1时，P30/P20的值不断减增大。也就是说，随着损耗系数的增大，逻辑或非门的输出效果越差。这是因为损耗系数为逻辑或非门的输入信号实际损耗和额定损耗的比值，实际损耗越大，或非门放大功能减弱，最终导致逻辑与门的输出效果变差[17]。

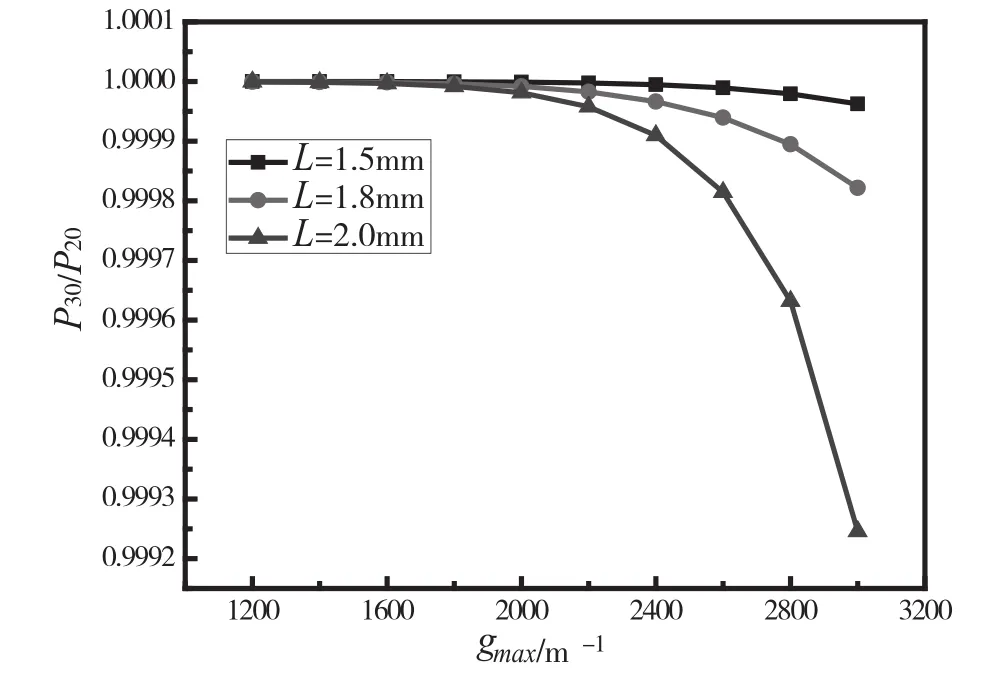
图7 最大模式增益与P30/P20的关系

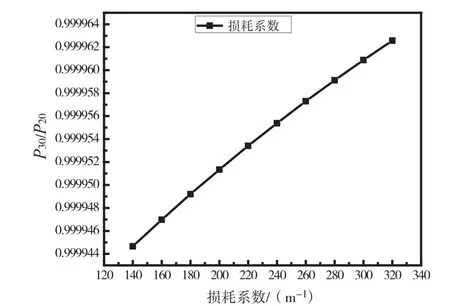
图8 损耗系数与P30/P20的关系

3 结 语

以P30/P20为指标，仿真分析了级联量子点半导体光放大器全光逻辑或非门的性能。研究结果表明：第一级输入电流越小，逻辑或非门的性能越好，而第二级输入电流对或非门性能影响很小；在一定范围内，输入连续光功率越大、有源区长度越长、有源区宽度越宽、最大模式增益越大、损耗系数越小，或非门输出效果越好。但是，在实际的应用中，需要结合实际情况选择合适的参数取值。