摩擦对斜齿圆柱齿轮啮合刚度影响规律研究

韩 林

（天津职业技术师范大学机械工程学院，天津 300222）

准确计算时变啮合刚度是对齿轮副进行设计或分析的关键一步，其重要性不言而喻。目前，计算齿轮啮合刚度的方法有4 种：有限元法[1-3]、解析有限元法[4-5]、解析法[6-9]和试验法[10-11]。其中，基于材料力学的势能解析法[6]由于其计算效率高，被广泛采用，特别适用于对齿轮传动系统进行动态特性分析。势能法将轮齿视为变截面悬臂梁，计算啮合力作用到齿面时的赫兹接触势能、剪切势能、压缩势能及弯曲势能等。众所周知，除在节线附近，主从动轮啮合点在其他啮合位置均存在相对滑动，产生摩擦力。在利用势能法计算齿轮副啮合刚度时，应考虑摩擦力。为此，Saxena 等[12-14]以势能法为基础，研究了直齿圆柱齿轮副中的摩擦力对啮合刚度的影响；Han 等[15]虽讨论了摩擦力对斜齿圆柱齿轮啮合刚度的影响，但当采用不同摩擦系数模型时，工况参数对啮合刚度的影响是否有所区别，其研究工作并未给出相关结论。此外，摩擦力对啮合刚度的影响程度，是否与斜齿轮副的螺旋角、模数等参数有关[16-17]，也未发现相关报道。针对上述问题，本研究以势能法为基础，计及齿面摩擦力的影响，通过采取不同摩擦系数模型，揭示工况参数对斜齿圆柱齿轮副时变啮合刚度的影响，探讨所述影响与斜齿轮副螺旋角、模数等参数之间的关系。

1 时变啮合刚度计算模型

1.1 势能法

啮合刚度计算模型如图1 所示。作用于该轮齿上的啮合力为F，可分解为径向、切向2 个方向上的分力Fa、Fb。

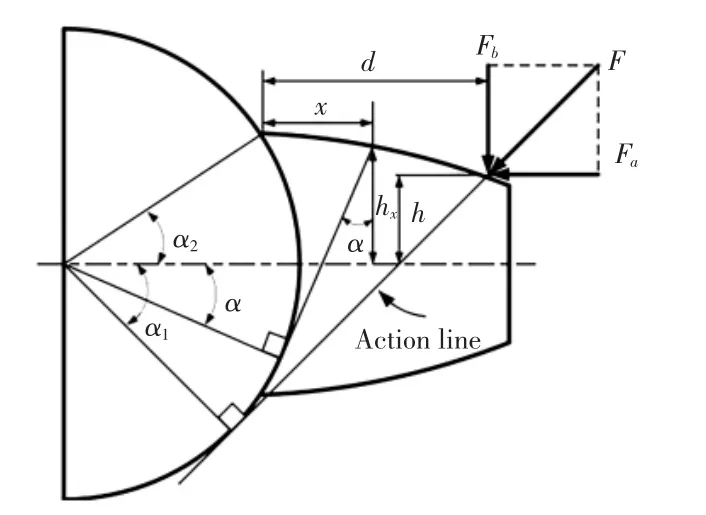
图1 啮合刚度计算模型

根据力学相关理论，存储于该齿内的势能包括赫兹接触势能Uh，压缩势能Ua，弯曲势能Ub及剪切势能Us，各项可表示为如下形式

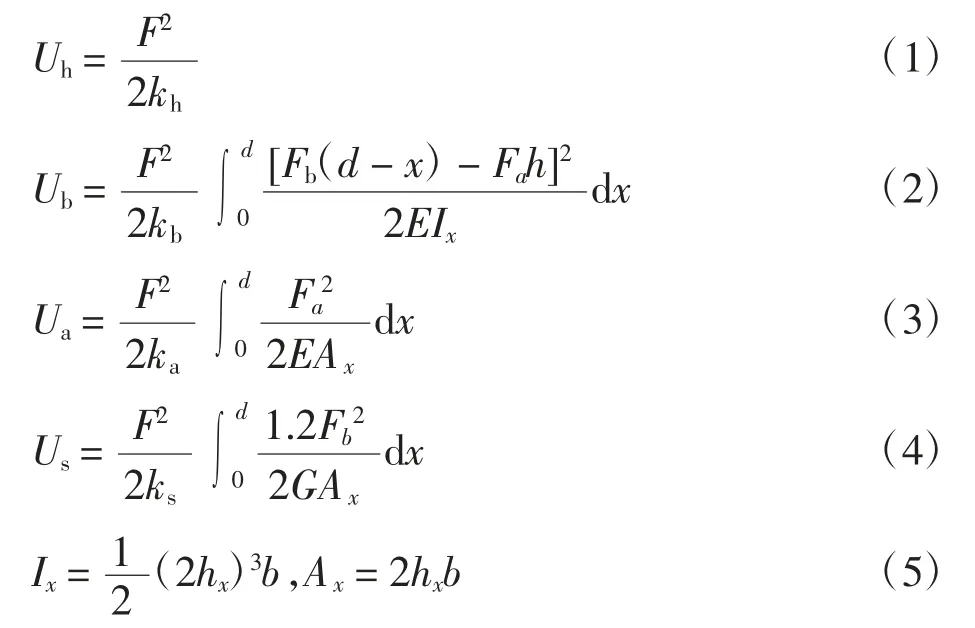
式中：kh、kb、ka、ks分别为赫兹接触刚度、弯曲刚度、压缩刚度和剪切刚度；G、E、b 分别为齿轮材料剪切模量、杨氏模量和齿宽；Ix、Ax为距离齿根距离为x 处的截面惯性矩及截面面积；hx为对应于到基圆径向距离为x、垂直于齿中心线的距离；d 为啮合力的作用点到基圆的径向距离。

Yang 等[18]的研究结果表明，式（1）中的接触刚度值kh实际上沿着整条作用线是一常数，与接触位置及穿入程度无关，可表示为

式中：v 为材料的泊松比。

除此表达式外，还需考虑载荷影响的经验公式[19]，为简化起见，此处采用式（6）。将式（5）代入式（2）-（4）中，得

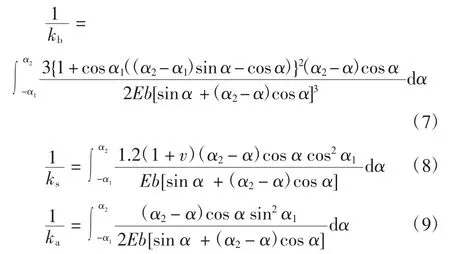
计算过渡圆角变形的几何参数如图2 所示。

考虑齿根基体变形[20]，相应的齿根基体刚度为

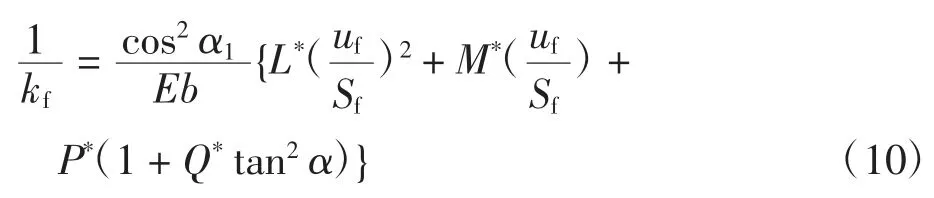
式中：uf、Sf如图2所示。

式中：Xi*为系数 L*、M*、P*、Q*，参数 Ai、Bi、Ci、Di、Ei和 Fi所涉及的参数值如表1 所示。hfi=rf/rint，rint如图2 所示。

图2 计算过渡圆角变形的几何参数

表1 公式（11）所涉及的参数值

根据上式，单齿对啮合刚度可表示为

式中：下标1、2 分别为主、从动轮。若一对齿轮副重合度为ε，则当有n=ceil（ε）对轮齿同时啮合时，其啮合刚度为

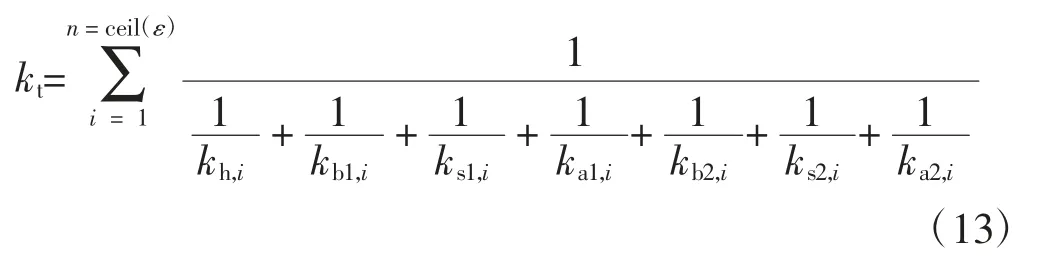
函数ceil（x）的含义是取比x 大的最小整数。

1.2 斜齿圆柱齿轮啮合刚度

与直齿轮不同，斜齿圆柱齿轮轮齿在啮合时，接触线与轴线不平行，且其长度是逐渐增大又逐渐减小。通常斜齿轮重合度 2 ＜ ε（ε = εα +εβ，εα 为端面重合度，εβ 为轴向重合度）＜3，斜齿圆柱齿轮啮合的作用面且对应于 εα ＞ εβ，如图3所示。

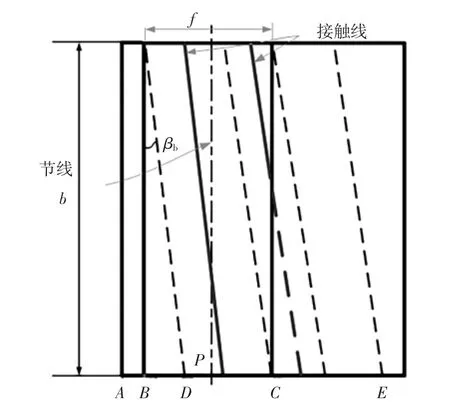
图3 斜齿圆柱齿轮啮合的作用面

从图3 可以看出，三齿对啮合的初始时刻，则单齿对接触线长度从进入啮合至退出啮合，可由下式计算获得

同理，对于每一对啮合轮齿，在一个啮合周期T内，其接触线长度可表示为

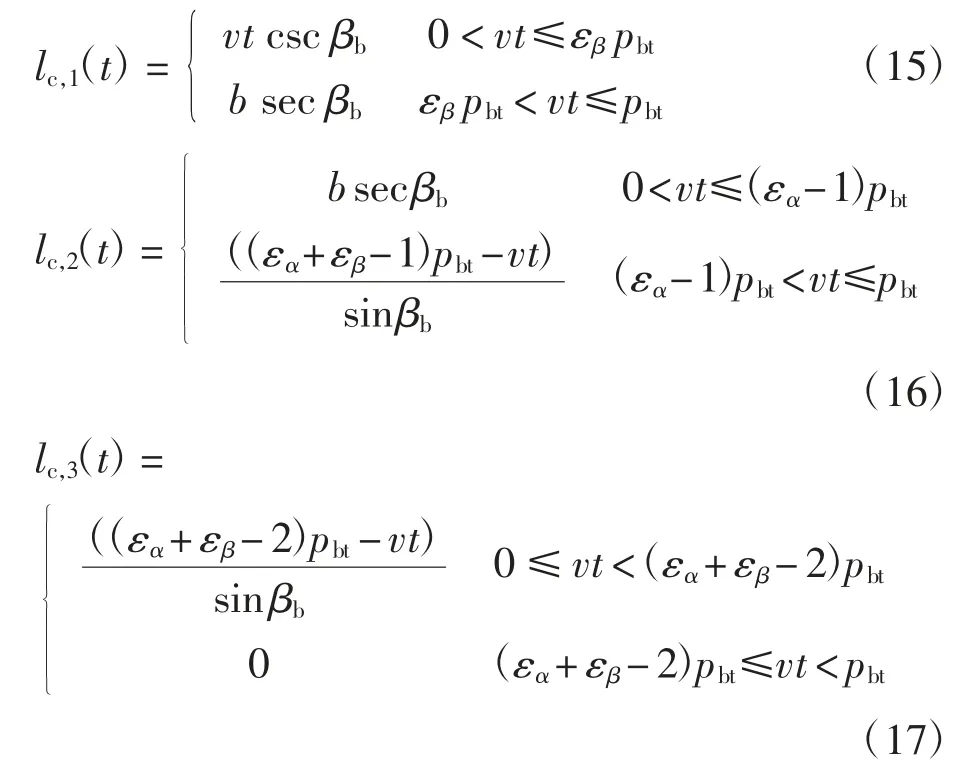
上述计算直齿轮啮合刚度的方法不能直接用于计算斜齿轮啮合刚度。为此，若将斜齿轮沿其轴线方向划分成诸多宽度为dy 的“切片”，则每一片即可视为一直齿轮。由此，可利用上述势能法计算每片直齿的啮合刚度，整齿啮合刚度可通过沿整齿齿宽的积分获得。切片法模型如图4 所示。

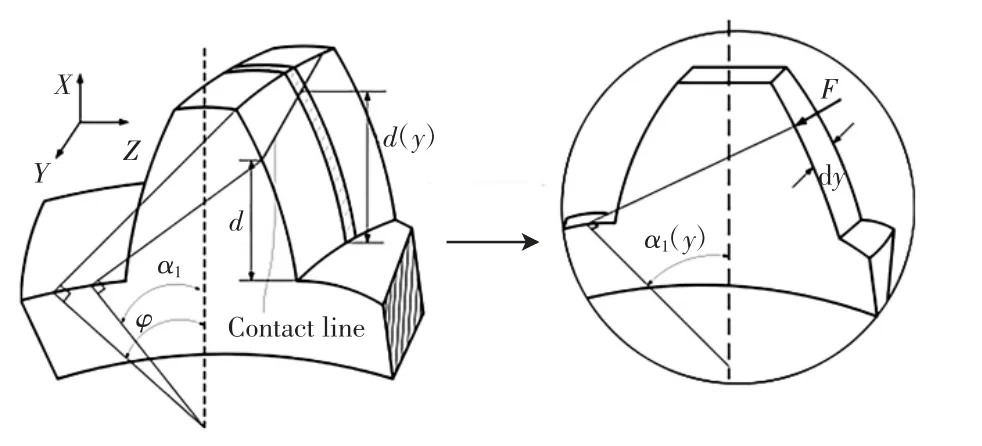
图4 切片法模型

作用于切片上的力如图5 所示。除啮合力F 外，与F 垂直方向上作用有摩擦力Ff，该摩擦力也可分解为 Ffa、Ffb，大小可由下式获取

式中：μ 为摩擦系数。

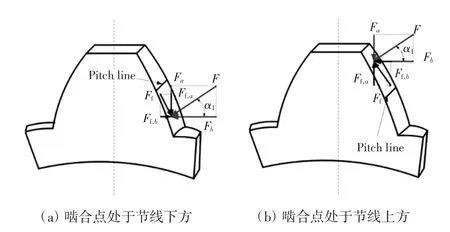
图5 作用于切片上的力

当接触线位于节线下方时，根据前述势能法原理，存储于每一切片的弯曲势能为

式中：dIx=（2hx）3dy/12，表示切片的截面惯性矩。

式中：参数α1（y）、d（y）、h（y）及x 如图1 所示。

将式（22）、（23）代入式（21），经整理，得

则有效接触线长度为l 的齿对弯曲刚度为

将x 和hx的表达式代入上式，同时由于上式求积分困难，故利用离散求和代替上式直接积分，可得

同理，当接触线位于节线上方时，有

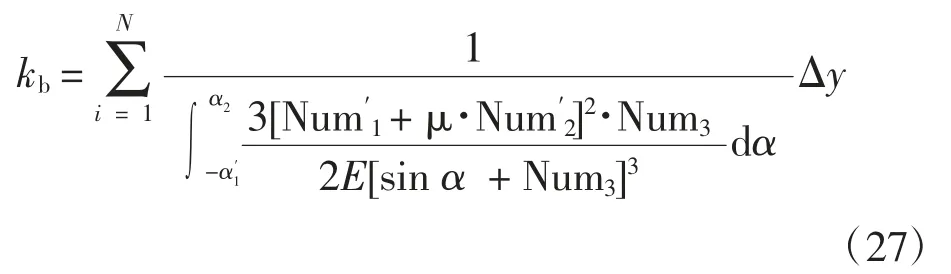
为简便起见，令

同理，可推导出剪切刚度的表达式

压缩刚度的表达式为

当某啮合齿对接触线部分位于节线之上，而另一部分位于节线之下时，该齿对弯曲刚度为

式中：N+为对应于接触线位于节线上部的切片数；N-为对应于接触线位于节线下部的切片数。

针对 2 ＜ ε ＜ 3 且 εα＞ εβ的情况，在整个啮合周期内，3 对啮合齿对的弯曲刚度分别为

式中：N1=lc，1（t）cos βb/Δy；N2=（lc，1（t）-（vt-lBP）/sin βb）cos βb/Δy；N3=lc，1（t）cos βb/Δy-N2；N4=（lBP+（εβ-1）pbtvt）/（Δy·tan βb）；N5=b/Δy-N4；N6=lc，2（t）cos βb/Δy；N7=lc，3（t）cos βb/Δy。

同理可得三齿对啮合的其他刚度项如ks，ka等，篇幅所限，此处不再列出。

1.3 摩擦系数模型

上述刚度表达式中的摩擦系数与工况及接触表面质量有关。本研究选用2 个摩擦系数模型，探讨工况参数和表面粗糙度对啮合刚度的影响规律及不同摩擦系数模型对啮合刚度影响的差异性。

BK 摩擦系数公式[21-22]

式中：η 为润滑油粘度，单位为cP；S 为用均方根值表示的齿面粗糙度，单位为μin；w 单位长度上的载荷，单位为lbf/in；us、ur分别为啮合点处相对滑动速度及卷吸速度，单位为in/s。该式中非标准单位在程序执行前，均通过与标准单位的关系转换。

Xu[23]根据非牛顿流体热弹流润滑理论提出了在节点处摩擦系数为零的摩擦系数公式为

式中：v0为在油入口温度下的绝对黏度（动力黏度），单位cPs；S 为表面粗糙度均方根值，单位μm；bi（i=1，2，…，9）为常系数，取决于润滑油类型，若为 75W90 齿轮油，则有 v0=10 cPs，bi=-8.92，1.03，1.04，-0.35，2.81，-0.10，0.75，-0.39 ，0.62 ；R 为有效曲率半径，单位 m，取决于齿轮几何特征及啮合位置；卷吸速度为Ve，跟齿轮转速有关；最大压力Ph取决于传递的载荷，由文献[24]所述方法获取，本文开发程序的有效性已在文献[25]中证实。

2 仿真结果与讨论

斜齿圆柱齿轮参数如表2 所示。

表2 斜齿圆柱齿轮参数

接触线长度和啮合刚度如图6 所示。从图6（a）可知，起始时间为轮齿刚进入啮合时刻，随着主动轮不断转动，接触线长度逐渐增大，然后保持一定值不变，又逐渐减小，直至退出啮合，接触线长度变为0。

摩擦系数公式不同，在相同工况条件下，所得摩擦系数分布情况不同。摩擦系数分布如图7 所示。

在负载扭矩T=600 N·m、表面粗糙度S=1.6 μm、主动轮转速n1=500 r/min 的工况条件下，2 种模型所获得的摩擦系数沿一对轮齿接触线方向上的分布情况。

从图7 中不难发现，BK 模型在整个啮合过程，摩擦系数差异性不明显，节线附近摩擦系数达到峰值；而Xu 模型所得摩擦系数在整个啮合过程分布差异较大，在节线附近达到最小值。

图6 接触线长度和啮合刚度

图7 摩擦系数分布

表面粗糙度对啮合刚度的影响如图8 所示。研究负载扭矩T=600 N·m，主动轮转速n1=500 r/min 的工况下，轮齿表面粗糙度对啮合刚度的影响规律。此处忽略了粗糙表面对赫兹接触刚度的影响。

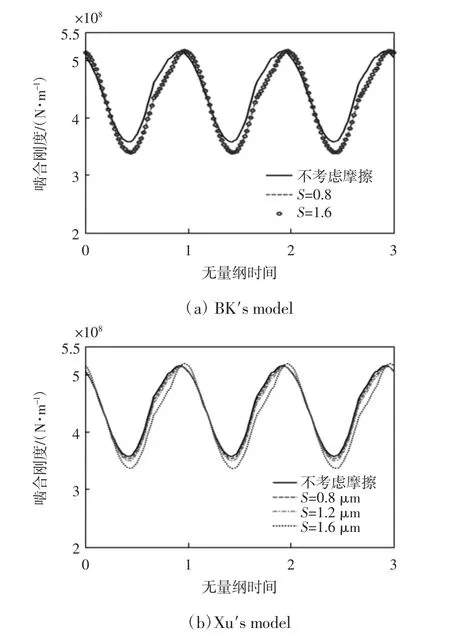
图8 表面粗糙度对啮合刚度的影响

从图8 可以看出，摩擦因素确实对齿轮副啮合刚度具有一定影响，且影响规律在整个啮合周期内并不一致，即部分时间段内是增大啮合刚度，而余下时间内则是减小啮合刚度，这主要是因啮合齿对在越过节线附近时，摩擦力换向所致；此外，从图8（b）可知，Xu的摩擦系数模型随着齿面粗糙度取值不同，其影响也随之表现出明显差异；而从图8（a）可知，BK 摩擦系数公式对齿面粗糙度不灵敏，摩擦系数变化不大，故对啮合刚度的影响趋于相同。

在S=1.6 μm、主动轮转速n1=500 r/min 的工况下，不同负载转矩对啮合刚度的影响如图9 所示。此处需要说明的是，本文所采用的刚度计算模型忽略了载荷对赫兹接触刚度的影响，故负载不同，摩擦系数不同，进而影响啮合刚度。从图9（a）和（b）可以看出，在不考虑对赫兹接触刚度影响的前提下，负载转矩对啮合刚度的影响不显著。

在之前的文献中，计算齿轮副啮合刚度时，未包括齿轮转速因素，即认为转速仅对啮合频率产生影响，对啮合刚度不会产生任何影响。而在本研究中，当计及摩擦因素对啮合刚度有影响时，由于转速会影响到摩擦系数，则势必会间接地对啮合刚度产生影响。主动轮转速对啮合刚度的影响如图10 所示。

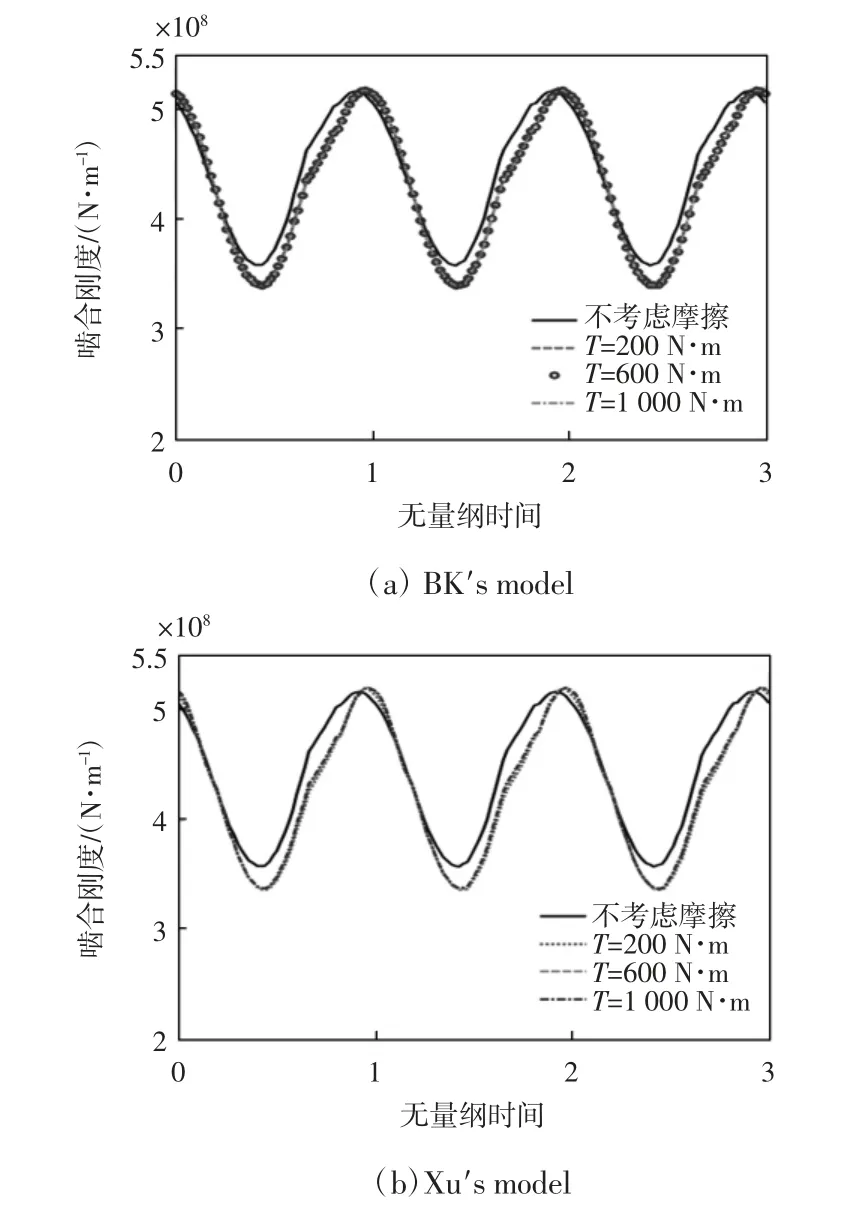
图9 不同负载转矩对啮合刚度的影响

图10 主动轮转速对啮合刚度的影响

由摩擦学理论可知，转速越低，接触表面间越不容易形成润滑油膜，摩擦系数越大，故图中当n1=100 r/min时，对应的摩擦系数值最大，其对啮合刚度的影响愈明显。然而，从图10 中可以看出，不同转速对啮合刚度的影响差异性不大。

以Xu 所提出的摩擦系数公式为例，探讨齿面摩擦对不同螺旋角、模数的齿轮副啮合刚度的影响特征，啮合刚度波动与齿轮基本参数之间的关系如图11 所示。

图11 啮合刚度波动与齿轮基本参数之间的关系

图中纵轴代表啮合刚度的波动量（定义为在1个啮合周期内，刚度最大值与最小值之差）。从图11（a）可知，螺旋角分别为 10°、12°、14°时，考虑摩擦及不考虑摩擦时的齿轮副啮合刚度的情况。不难看出，随着齿轮副螺旋角的增大，考虑摩擦因素的刚度值与未考虑摩擦因素的刚度值之差逐渐减小，即摩擦因素对啮合刚度的影响逐渐减小。从图11（b）可知，齿轮法面模数分别为2.5 mm、3 mm、4 mm 时，摩擦对啮合刚度波动量的影响规律与螺旋角情况不同，摩擦对齿轮副啮合刚度的影响随着模数增加变化不大。

3 结 论

本研究考虑斜齿圆柱齿轮副啮合时的齿面摩擦力，在势能法的基础上，改进了啮合刚度计算模型。同时，以2 种摩擦系数公式为例，探讨了摩擦对啮合刚度的影响及不同摩擦系数模型之间的差异性。研究结论如下。

（1）摩擦因素对啮合刚度有一定的影响，在计算啮合刚度时，应予以考虑。

（2）在1 个啮合周期内，摩擦对啮合刚度的影响不一致。

（3）摩擦系数模型不同，工况参数对啮合刚度的影响规律也不尽相同。

（4）摩擦对啮合刚度的影响随着螺旋角的增大而减小，而随着模数的增加，影响不明显。

基于上述工作，探讨摩擦对系统动力学行为的影响有待进一步深入研究。