单点交叉口行人机动车协同优化方法
徐明杰,焦振珅,卞 慧,韩 印,刘学刚
(1 上海理工大学 管理学院,上海 200093;2 北京物资学院 信息学院,北京 101149)
0 引言
交叉口是两条或两条以上道路的交汇处,是车辆、行人交通汇集、转向和疏散的必经之处。而大多关于城市道路交叉口的信号研究,都是在忽略城市道路上行人的影响下进行的。但实际上,城市道路都是各种机动车、非机动车和行人等多种交通方式混合通行的。中国大城市普遍拥堵的主要原因之一就是多种交通方式混合通行,不易进行控制造成的。当前,随着机动车数量的猛增,城市道路交通拥堵问题愈发严重,行人的出行过街问题也愈加突出。因此,作为交通参与者的行人也需要被纳入到信号配时体系中。
在城市道路网中,关于交叉口信号配时优化,国内外学者专家进行了大量研究。杨晓光[1]等针对交叉口信号配时提出了相应的理论和方法,利用波动理论和车流运行的时空图,建立了交叉口通行能力和损失通行能力模型,给出了在信号协调控制方面的建议。姚荣涵[2]等针对交叉口渠化左转短车道的情况,研究其时空资源的最优配置。通过分析短车道对进口道饱和流率的影响,建立以交叉口通行能力最大化与车均延误最小化,以短车道长度和相位有效绿灯时间为决策变量的多目标优化模型;刘岩[3]等为了解决过饱和状态下的信号交叉口路段长度对延误影响的问题,推导出了基于过饱和信号交叉口最大延误模型。通过对经典延误模型的分析和利用排队长度与延误关系,推导出适用于该状态下的延误模型,并且给出了最大延误计算方法;齐立群[4]等以增大系统的通过量为目标,研究了最短车辆排队长度和相位差之间的函数关系,利用波动理论研究上下游之间最短车辆排队长度的形成及其计算方法;肖秀春[5]等将延误作为信号延误的目标函数,以信号时长、有效绿灯时间为约束条件建立信号配时模型。通过寻求目标函数的最小值来获得最优信号周期与有效绿灯时间,最后通过实例验证可行性;游黄阳[6]等从中国城市交叉口的交通特征入手,在考虑排队长度和行人过街约束条件下,构造了多目标规划函数。建立的优化目标是使车辆平均延误和各相位关键车道组饱和度方差最小,约束条件是排队长度不超过车道的预设长度,且保证行人过街相位足够长;刘妍[7]等应用store-and-Forward理论和排队论,描述路段上车辆到发平衡状况。重点研究交叉口控制参数的优化,其中参数的优化包括相位差的优化和绿信比的优化。在保证各需求个体具有公平的道路使用条件下,以避免短支路上排队上溯和干道上需求的快速疏散,综合考虑排队大小及排队急迫程度2 个指标,建立了一个特殊的非线性规划模型。
与此同时,关于行人过街信号控制也受到了不少的关注。Wanjing ma[8]等通过分别建立单点信号控制交叉口下的行人专用相位、机动车兼顾行人相位下的定量准则模型,并将其纳入到统一的经济框架之下。通过敏感性分析,给出了行人专用相位的设置条件。杨晓光[9]等运用穿越理论,推导在行人通行时,穿越行人的转弯车辆通行能力模型和行人延误模型;在此基础上,通过设置专用相位前后的评价指标对比,论证了整个交叉口行人专用相位的条件;Chunhui yu[10]认为,行人过路需求是分布在主干道的两侧,需求起点、目的地构成了行人过路网络,并提出了一种同时优化中分块人行横道的数量、位置和信号设置的综合模型,以实现行人与车辆运行性能的最佳权衡;YangZeng yi[11]基于遗传算法,开发了一种有效的方法,来完成十字路口行人和车辆的信号优化;Xiang Li[12]等提出了一种改进交叉口交通性能的多目标优化方法,并在交通系统微观仿真中,考虑了车辆冲突和行人干扰。针对机动车流和行人流,优化了信号配时和车道分配。
结合上述国内外的研究资料,本研究将同时考虑行人、机动车之间的信号优化,建立单点交叉口行人-机动车协同优化模型,并与不同的智能算法相互对比,从而获得最佳信号方案。
1 信号优化模型
延误是评价交叉口运行状况的重要指标,据相关研究显示,每年通勤者因延误带来不少的经济损失。因此,本文研究的主要目标是,降低整个交叉口行人、机动车的总延误。
1.1 机动车延误模型
机动车平均信号控制延误模型,采用了美国交通研究委员会的《道路通行能力手册》中的延误计算方法,模型表述如式(1)~式(4):

其中,dv表示整个交叉口的平均延误;表示第i相位j个进口道的平均延误;表示均匀延误;表示增量延误;表示由于初始排队而导致的延误;c为交叉口的周期时长;gi表示第i相位的有效绿灯时间;T表示调查交叉口的观测时间;K、I为修正系数;qij表示第i相位j个进口道的车流量。
1.2 行人延误模型
行人过街的延误,主要取决于行人过街时等待过街信号而产生的信号延误,及转弯机动车对行人产生干扰条件下的延误。因此,行人的平均延误模型将由信号延误和右转机动车对行人过街产生的冲突延误构成。由于行人过街存在不稳定性,需对行人过街的行为做出以下假设:行人的个体状态稳定,不存在违反交通法规的现象;在行人与右转机动车的冲突点处,行人将寻找合适的安全间隙来通过;行人与行人之间的冲突不做考虑;行人是以单排多列的形式通过。
(1)行人信号延误模型[15]。行人信号延误模型表述如式(5)、式(6):

在式(5)、式(6)中,ts表示消散等待过街行人的时间;s表示行人信号开启时,等候过街行人的饱和流率;ti表示第i 相位绿灯损失时间;th表示第i相位的红灯时间;qp表示过街行人的到达率。
(2)转弯机动车辆对行人的冲突延误模型。转弯机动车辆与行人冲突延误模型表述如式(7):

其中,k表示转弯车流的流量,u表示行人过街所需的最小间隔时间。由此可得信号交叉口第i相位行人平均延误模型:

则整个交叉口的行人平均延误如式(9):

考虑行人的交叉口信号优化目标函数如式(10):
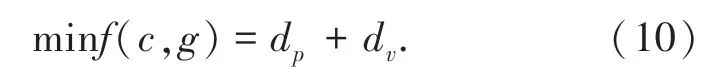
行人与机动车信号约束如式(11)~式(14):

其中,式(11)约束表示周期约束;式(12)约束表示有效绿灯时间约束;式(13)是最小绿灯求解公式,其意是用于消散本相位内所到车辆数的最小绿灯时间;式(14)是所有有效绿灯时间之和与交叉口整体损失时间之和,必须等于周期时长的等式约束。
2 优化算法
通常情况下,用于交叉口信号配时的算法是webster,只需要调查相关数据带入该模型中便可得出相应的信号方案。考虑到本文提出的信号优化模型是非线性的,因此需要考虑适合该模型的求解方法。该模型常用粒子群算法(pso)、遗传算法(ga)、内点法求解。
2.1 粒子群算法(pso)
粒子群算法是群体优化算法,源自于鸟类捕食的启发。粒子群算法首先在约束条件所围成的可行域范围内初始化一群粒子,每个粒子都代表优化过程中的潜在解。每一个粒子使用位置、速度、适应度值三项指标表示该粒子特性,适应度值由事先编好的适应度函数计算获得。适应度值的大小用于评价粒子的好坏与否和确定粒子下一次更新位置与速度。粒子在解集域内活动,通过追踪个体极值Pbest和群体极值Gbest 更新位置。粒子每更新一次位置,就计算适应度值,然后通过比较新粒子适应度值、个体极值、群体极值来更新个体极值和群体极值位置,通过一次次的迭代求出解。
2.2 遗传算法(ga)
遗传算法是一种自适应启发式搜索算法,旨在利用自然选择和遗传的进化思想来解决优化问题。遗传算法的进化始于随机产生的候选解的总体,也称之为种群。评估每个个体的适应度,选择更合适的个体,然后重组或可能随机变异,以创造一个新的种群,称为新一代。新一代将被用来创造下一代。重复迭代过程,直到达到所需的适应度级别或已创建预定义的最大生成次数。它是一个强大的方法,应用于具有非常大的候选解集和复杂的搜索空间的问题。因此,对该优化问题进行了遗传算法的实现。
2.3 内点法
内点法是一种用于求解非线性模型的算法,本质上是约束优化算法。通过引入效用函数的方法,将约束优化问题转换成无约束问题,其间再利用优化迭代的思想,不断寻求满足约束的最优解,使得算法收敛。
3 案列分析
本研究选取上海市杨浦区某一交叉口为测试现场,该交叉口为十字形交叉口。其中东西方向为主干道,南北方向为次干道。东西方向为双向六车道,南北方向为双向四车道,相位方案为东西直行,东西左转,南北直行,南北左转。交叉口的道路渠化如图1 所示;现状调查流量、信号方案见表1、2。
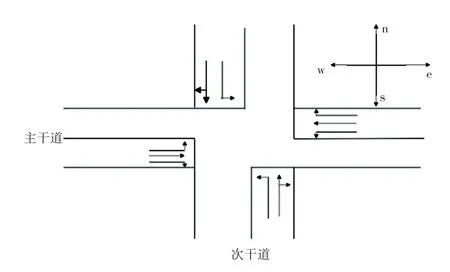
图1 现状交叉口道路渠化图Fig.1 Road channelization diagram at the current intersection
依据调查得到的数据,利用python 语言编写pso 算法程序。程序的配置环境为Pycharm2020,设置算法的迭代次数为200 次,初代粒子为200 个,其它相关的算法参数参考相关文献。遗传算法以及内点法相关程序均在Matlab 配置环境下编写,结果汇总见表3。
从优化效果可见,pso 算法对比现状车辆延误、行人延误分别降低了20.8%和20%,ga 算法对比现状车辆延误、行人延误分别降低了23.2%和23%,内点法对于现比状车辆延误、行人延误分别降低了23.2%和28%,webster 算法对比现状车辆延误、行人延误分别降低了12%和8.5%。总体而言,这些算法都能有效的解决模型求解并生成较优方案,证明了研究所提出模型和算法的有效性。从各自算法优化的结果上看,智能算法ga 和pso 相差不大,性能方面pso 更好。然而,内点法在性能上和结果上均优于其它算法。

表2 信号配时方案Tab.2 Signal timing scheme

表3 各种算法优化效果对比Tab.3 Comparison of optimization effects of various algorithms

图2 遗传算法性能收敛图Fig.2 Convergence diagram of genetic algorithm performance
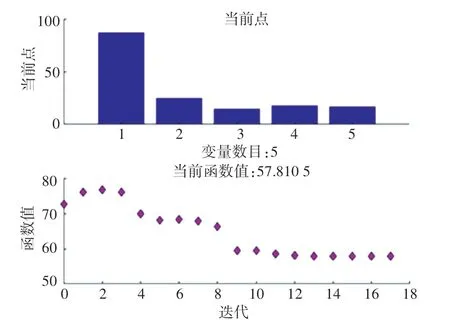
图3 内点法性能曲线图Fig.3 Performance curve of interior point method
4 结束语
研究以降低行人机动车的延误为目标,建立了行人机动车协同配时模型,并采用了不同算法对模型进行了求解分析。对比现状和常规的webster 算法,各算法均表现良好,验证了模型以及算法的有效性。但研究未能考虑到行人机动车的冲突问题,此外交叉口并不是独立存在的,未能考虑到上游交叉口对下游交叉口产生影响等问题。下一步将会对上述研究存在的不足进行进一步研究,以期获得良好的交叉口运行状况。

