基于多阶段向量量化算法的研究
刘丹青,李明勇
(1 东华大学 计算机科学与技术学院,上海 201620;2 上海市计算机软件评测重点实验室,上海 200235)
0 引言
随着互联网的快速发展,计算机技术已渗入到社会的各种行业。因此,高维的文本、图片、视频等多媒体数据呈现爆炸式的增长趋势[1]。传统的暴力搜索方法是通过遍历所有的数据点进行查询,随着数据集的增大,这种暴力搜索方法需要巨大的存储空间,并且每次检索的时间很长。因此,该方法只适用于小规模的数据集。针对大规模高维数据集的查询问题,研究者们提出了近似最近邻搜索方法,在可接受一定精度损失的情况下,查询到尽可能精确的结果。其中,基于向量量化的近似最近邻搜索方法是比较有效和受关注较多的方法之一。该方法可以有效地降低空间存储,提高检索速度。
向量量化[2]的基本思想是,仅用数据集特征向量空间中的一个有限子集,表示该数据集特征向量空间中所有数据集特征向量,因而大大减少了数据的内存存储。常用的向量量化方法有树搜索向量量化方法、乘积量化方法[3]和多阶段向量量化方法[4-5]等。本文着重研究多阶段向量量化方法,并对基于多阶段向量量化的近似最近邻搜索方法提出改进。在训练码本过程中,通过优化初始聚类中心,减小重构向量的均方误差,改善码本质量,进一步减小向量的量化误差,以此提高实验召回率。
1 相关工作
1.1 最近邻搜索
最近邻搜索在计算机视觉、多媒体搜索、机器学习等领域里应用非常广泛。最近邻检索就是给定数据集和目标数据,根据数据的相似程度,从数据库中查找与目标数据最接近的数据。一般情况下,可认为在空间中,两个数据点的距离越小,其之间的相似性越高。
假设,给定一个查询向量q,最近邻搜索的目的,是在一个向量集合X={x1,x2,…,xn} 里,找到与查询向量q距离最近的目标向量x*:
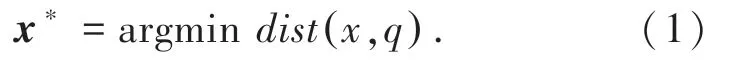
其中,dist(x,q)是目标向量和查询向量之间的距离。通常使用欧氏距离(Euclidean distance)定义两向量之间的距离,即两个数据点在空间里的直线距离。在D维空间中,两个数据点(A1,A2,…,AD)和(B1,B2,…,BD)之间的欧式距离可以表示为:
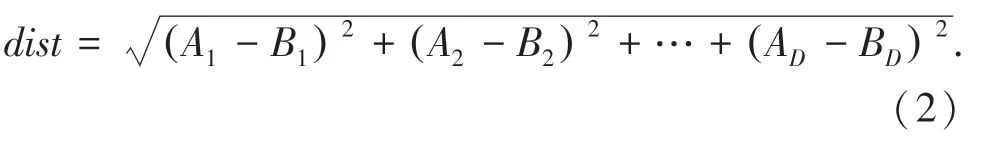
1.2 近似最近邻搜索
面对数据库中巨大的高维数据,当前基于最近邻搜索的检索方法不能得到理想的检索结果和可接受的检索时间。因此,为了较好的均衡准确性和资源,人们开始关注近似最近邻检索方法ANN(Approximate Nearest Neighbor)[1]。
近似最近邻搜索是给定一个查询向量,为了用尽可能低的空间存储成本,查找数据库中与之最相似的向量,在牺牲可以接受的精度范围内,加快检索速度。近似最近邻查询方法主要分为两类,一是基于哈希的方法,另一种是基于向量量化的方法。
基于哈希的方法是将数据映射到汉明空间,即通过哈希函数,将向量x转换成哈希码(海明码)b,通过二者哈希码的汉明距离,度量两个数据点之间的相似度,即将距离dist(x1,x2)近似成哈希码的距离dist(b1,b2)。基于哈希的研究方向主要是学习优化哈希函数。随着二进制化后数据信息的减少,准确性也随之降低。为了解决这个问题,近年来人们提出了各种基于向量量化的近似最近邻搜索方法。
1.3 向量量化
向量量化(Vector Quantization)多被应用在源编码和信号压缩方面[2]。向量量化是通过聚类方法,将向量集合聚类成多个类别,每一个类别里的向量都可以用其对应的类中心近似代替。换句话说,就是用其中的一个有限子集编码,表示一个向量数据空间中的向量。相对于需要存储原始数据的向量方法,向量量化方法只需要存储向量对应的类中心(即码元)的索引ID,大大减小了向量的存储空间。另外,只根据聚类中心的ID 去查找预先计算好的表格,其中存放着聚类中心与查询向量的距离。向量的欧式距离可以通过编码后码元之间的距离来近似表示,减少了计算时间,使得查询更加有效,提高了向量的检索速度。
人们开始重点关注将向量量化技术应用到近似最近邻搜索方向[3,5-11]。其中比较具有代表性的方法是乘积量化算法[3]。该算法的主要思想是,将高维的特征向量空间划分成若干个低维的子空间,对每个低维子空间的子特征向量进行量化,原始高维向量的量化结果就可以通过连接这些子特征向量量化后的编码进行表示。乘积量化是通过对每个子空间单独量化,从而减小量化误差。
乘积量化划分子空间的基本假设是,不同子空间内的向量分布是相互独立的,不存在关联。若子空间中数据分布之间的相关性很强,则乘积量化的性能就会下降。在实际情况中,真实的数据分布并不满足子空间相互独立的假设。因此,考虑到数据的分布,从而对数据进行更有效的量化。Juang 和Gray 等人提出了多阶段向量量化(MSVQ)[4]。在数据原始维度下,通过多个低复杂度的量化器,保留每次量化产生的误差,然后继续量化误差,使得量化误差进一步减小,从而提高近似最近邻检索方法的精度。
2 多阶段向量量化
多阶段向量量化方法和传统的向量量化方法不同,它并不是抛弃量化误差,而是保留量化误差,将其作为余差向量,进一步量化,从而减小量化误差。为了减少计算和存储,MSVQ 是使用几个阶段的码本,按顺序(即逐阶段)进行量化,之后连接每个阶段的量化结果表示输入向量。
多阶段向量量化是在原始高维空间上处理向量,通过多个低复杂度的量化器,由粗到细的量化向量,每一个阶段的输出是上一阶段量化产生的余差向量,将其作为下一阶段的输入再进行量化。有序的将每一阶段的量化器串联起来,每一阶段对应着一个由k-means 聚类算法得到的码本。
在训练阶段,通过在训练集X上进行k -means聚类,得到第一阶段的码本C1,将X在第一阶段码本上进行量化,得到其在C1对应的码元向量。第一阶段量化器的输出,即为X与其量化后码元向量的余差R1;R1作为第二阶段量化器的输入,在其上进行k -means 聚类,得到第二阶段的码本C2。将R1在第二阶段的码本上进行量化,得到其在C2对应的码元向量,第二阶段量化器的输出即R1与其量化后对应的码元向量的余差R2。
上述过程将持续至得到M个码本,即C=[C1,C2,…CM]。因此,原始向量可以表示为:

其中,Bi为码元索引,RM为第M 阶段的余差向量,即全局量化误差。
2.1 向量的编码和解码
在编码阶段,只需要存储向量对应的类中心的索引ID。因此给定数据集向量X和码本C1,C2,…,CM,在对应阶段码本里寻找使得当前阶段编码误差Ei最小的码元向量,即与当前所要量化的向量距离最近的码元向量,其对应的索引ID为Bi,也称为向量的编码。原向量即可表示为:
最后一阶段的编码误差E 可以忽略不计:

因此,多阶段向量量化算法可以根据向量编码近似地还原出原始向量,即重构向量。可以表示为所有阶段对应的码元向量之和。假设向量X的编码为[B1,B2,...,BM]∈{1,2,...,K},通过编码找到其对应阶段码本对应的码元向量,那么还原X的过程为:

2.2 距离计算
在查询过程中,数据库中的特征向量通过量化进行高效的压缩存储,也需要从数据库中尽快的查找到和查询向量相匹配的最近压缩向量。Jegou 等人提出了两种距离计算方法[3],分别是对称距离计算(SDC)和非对称距离计算(ADC)。
对称距离计算需要将查询向量x和数据库向量y都进行量化,得到q(x)和q(y)后计算二者之间的距离d(q(x),q(y)),即d(x,y)=d(q(x),q(y))。非对称距离计算,只对数据库向量y进行量化得到q(y),则x和y的距离d(x,y)就可以用查询向量和量化后的数据库向量之间的距离表示,即d(x,y)=d(x,q(y))。非对称距离计算进一步降低了量化误差,因此本文采用非对称距离计算。
查询向量q与重构向量的欧式距离为:
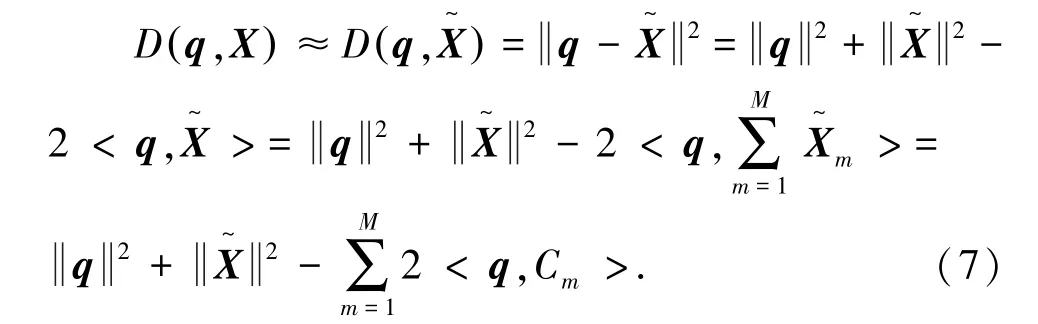
3 最小化均方误差的多阶段码本训练
本章提出在多阶段向量量化方法的训练码本进行改进,可减小量化误差,提高量化精度,从而提高实验的召回率。
多阶段向量量化方法在训练码本过程中采用经典的k-means 聚类算法。其主要思想是将空间中的k个点作为聚类中心(质心),进行聚类过程,对与它们最相近的数据进行归类。通过迭代更新每个类别里的质心的值,直至得到最好的聚类结果。虽然k-means 聚类算法应用广泛,但也存在着一些缺点:如,对噪音和异常点十分敏感。在初始化时,一般是随机选择初始的聚类中心,如果大多数聚类中心被分配到同一个簇中,那么聚类算法很有可能不会收敛。也就是说,初始聚类中心的选取会影响到聚类的收敛效果,导致影响最终的聚类结果。
为了避免初始聚类中心的选取影响聚类结果,本文提出最小化均方误差的多阶段码本训练方法,尽可能地选择相互之间距离较远的数据点作为聚类中心。通过优化初始聚类中心,改善训练出的码本质量,从而减小向量的重构误差,提高检索精度。具体实现步骤为:
(1)从数据集合的n个特征向量中随机选取一个特征向量。
(2)从剩余的n -1 个特征向量中按照一定概率(),选取聚类中心xj∈X,作为下一个聚类中心。该概率策略是数据点距离所有的聚类中心越远,其被选取的概率越大,反之,其被选取到的概率越小。
(3)依次进行上述过程,直至得到k个聚类中心。
初始的聚类中心的选取原则是:令其相互之间的距离要尽可能的远,逐个选取k个聚类中心,距离其它聚类中心越远的数据点,被选作下一个聚类中心的概率越大。
本文将上述方法应用到多阶段向量量化方法的训练码本过程中,该方法以最小化均方误差(Mean-Square Error,MSE)为目标,使得向量量化后的重构向量更精确。最小化均方误差计算如式(8)所示:
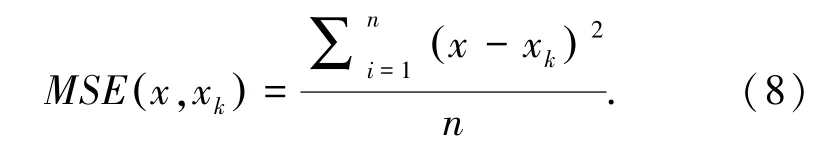
4 实验结果与分析
实验选用近似最近邻搜索最常用的一个公开数据集来进行实验性能评估,即SIFT1M 数据集[3]。数据集包含3 个子集:训练集、数据库集、查询集。SIFT1M 中的训练数据集是从Flicker 图片[12]分享网站上公开图像数据中提取的局部特征描述符,其数据集中的每一个特征向量都是128 维;样本数据集和查询数据集是由INRIA Holidays[12]数据库中的图像数据提取的特征描述符。训练数据集用于训练学习得到码本,样本数据集和查询数据集用于评估最近邻搜索的性能。本文主要采用召回率R1@100作为性能指标,即查询准确率,表示在查询阶段查询到的向量与验证数据集中的前100 个做对比得到的结果。数据集具体信息见表1。
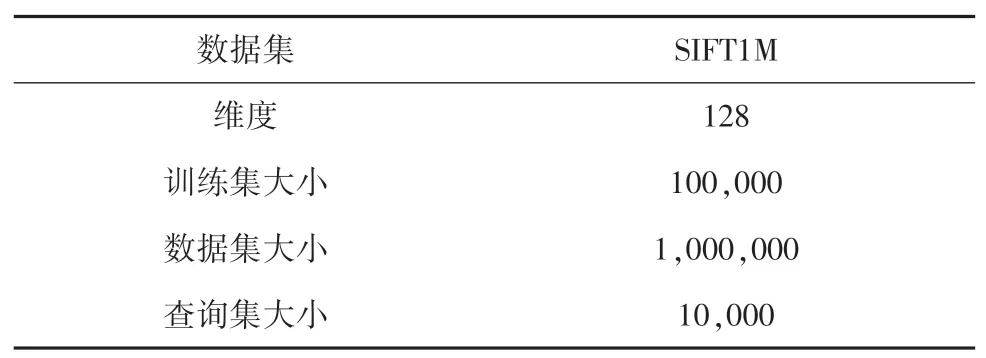
表1 SIFT1M 数据集Tab.1 SIFT1M dataset
实验设置码本数目为6,7,8,9,聚类中心数目K 为16,64,256。SIFT1M 数据集上的码本数目-均方误差的实验曲线如图1 所示。可以看出,本文提出的最小化均方误差多阶段码本训练方法曲线(IMSVQ),始终保持在多阶段向量量化方法曲线(MSVQ)的下方。表明本文方法可以进一步降低向量编码的量化误差,使得向量量化更精确。
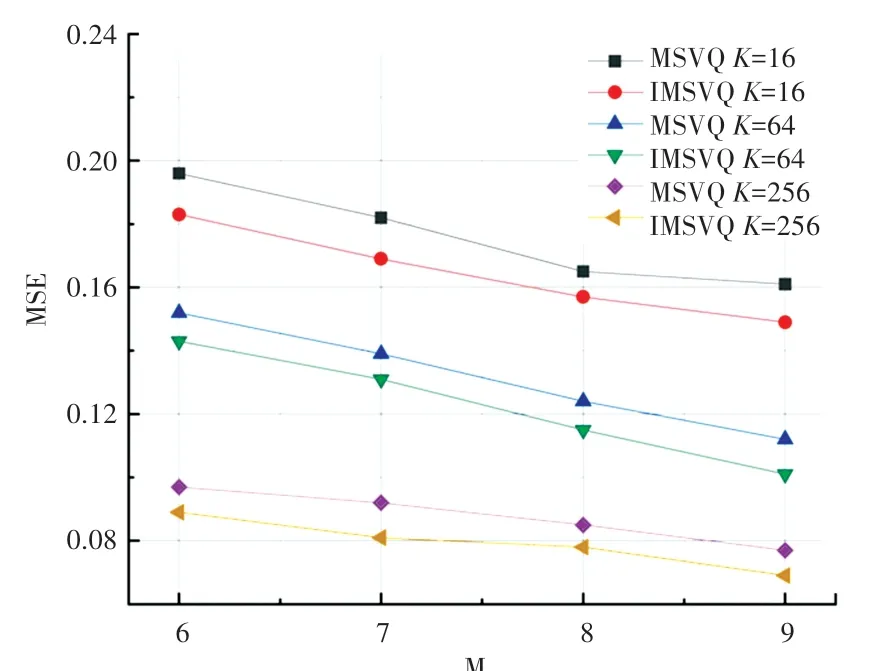
图1 码本数目-均方误差(SIFT1M)Fig.1 M-MSE(SIFT1M)
由于码本数目和码本中聚类中心数目是影响实验的重要因素。通过实验可以看出,在码本聚类中心数目保持不变的情况下,随着码本数目的增加,向量编码的均方误差逐渐降低。在码本数目保持不变的情况下,随着码本聚类中心数目的增加,向量编码的量化误差逐渐降低。因此选取合适的码本数目和码本中聚类中心数目可以提高实验性能。
SIFT1M 数据集上的实验迭代次数-召回率曲线如图2 所示。实验结果表明,在不同迭代次数下,本文提出的最小化均方误差的多阶段码本训练方法,性能优于多阶段向量量化方法。随着实验迭代次数的增加,从整体上看实验召回率逐渐增加。最小化均方误差的训练码本方法实验曲线始终保持在多阶段向量量化方法曲线上方,表明本文提出的方法可以有效地提高实验召回率。图3 是在SIFT1M数据集上的码本数目-召回率曲线。可以看出,优化初始聚类中心后的方法召回率高于多阶段向量量化方法。
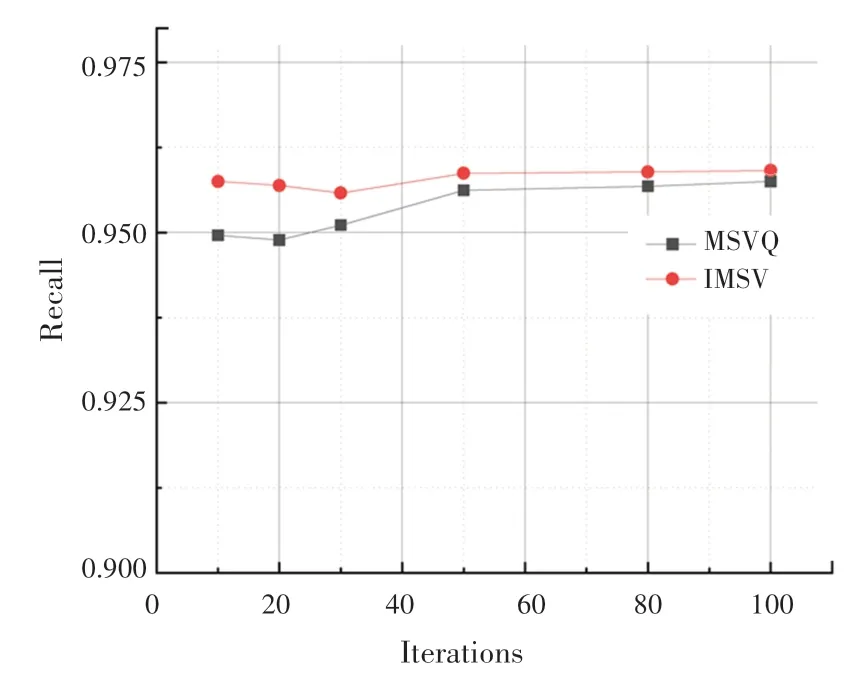
图2 迭代次数-召回率(SIFT1M)Fig.2 Iterations-Recall(SIFT1M)
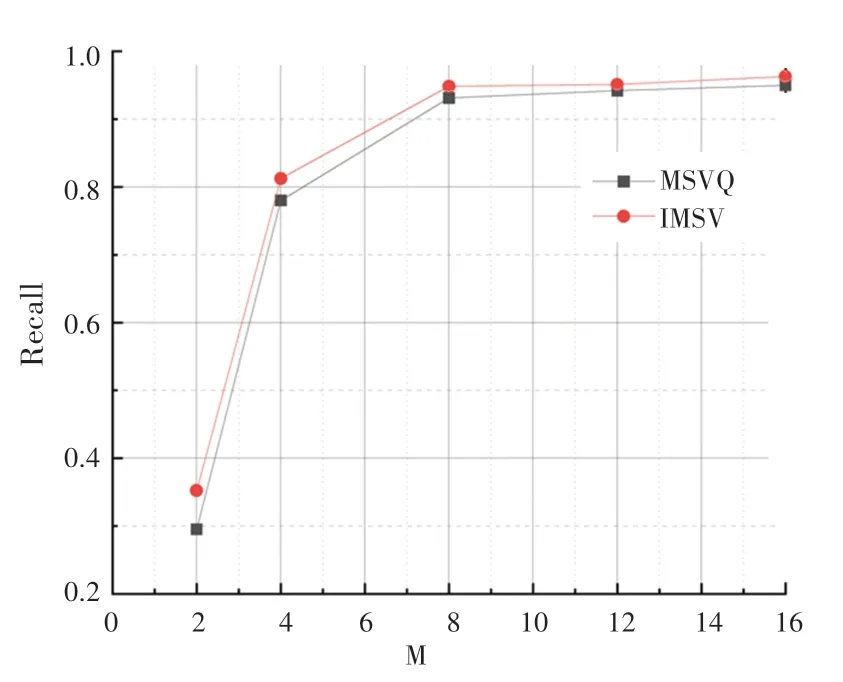
图3 码本数目-召回率(SIFT1M)Fig.3 M-Recall(SIFT1M)
综上所述,优化初始聚类中心,可以减小向量的量化误差,从而提高查询的召回率,证明本文提出的最小化均方误差的多阶段训练码本方法具有可行性和有效性。
5 结束语
本文在多阶段向量量化方法的训练码本过程中,提出了一种新的码本训练方法。原始训练码本的方法通过随机选择初始聚类中心,导致大多数聚类中心被分配到同一个类别中,向量量化后的重构向量不够精确,与原始向量相比误差较大,影响训练得到码本的质量。因此,为了减小随机选取初始聚类中心对训练得到码本质量产生的影响,本文采取选择距离较远的数据点原则,各个类别中的聚类中心差异度明显。以最小化均方误差为目标,通过优化初始聚类中心,减小向量编码的量化误差,有效地提高了聚类结果的准确性。
通过在公开数据集SIFT1M 上的实验结果表明,在近似最近邻搜索应用中,本文提出的最小化均方误差多阶段码本训练方法优于多阶段向量量化方法,可以进一步地减小向量编码的量化误差,提高查询精度,证明了该方法的可行性和有效性。

