基于动态规划的车站值班员交接班优化研究
孔德扬 高磊 吕晨
摘 要:為提升交接班环节的交接效率,减少无用项点的交接,本文现将交接班中的项点进行归纳总结,分析其重要性,将交接班时间指标作为背包容量,将交接班项点重要性作为物品价值,将交接班问题转换成0-1背包问题,利用动态规划法进行求解。以哈密东站车站值班号院交接班项点为算例,结果显示剔除冗余项点后减少了交接班时间,对于作业安全影响较小,对于现场交接班作业具有一定的指导意义。
关键词:车站值班员;交接班;动态规划
车站值班员是铁路运输调度指挥中的基本岗位,车站值班员工作范围涉及施工、接发车、调车与故障处理等,交接班环节异常重要。但是现场交接班普遍存在简化过程,一方面真正用于交接班的时间分配较少,交接期间涉及点名、文电传达与班前提问等环节,加之交班人员着急乘坐通勤车辆等,造成交班人员选择性交接,容易漏交、错交;另一方面由于各站在车站值班员交接班环节反复出现问题,各级管理人员将交接班项点不断增加,造成项点过于繁杂、冗余。
因此,本文从另一个角度来分析车站值班员交接班环节问题,即减少交接班项点,强化执行能力,从“多而乱”的状态转换成“少而精”的情况,但是减少的项点对于行车安全必须有较少的影响,从而保证车站值班员能够真正执行交接班的相关要求。
1 现行交接班问题及对策分析
1.1 优化交接班环节
各站交接班普遍是由点名、文电传达、班前提问、重点事项强调和对号交接班四个环节构成,其中点名、文电传达、班前提问和重点事项强调环节由值班主任将车站所有作业人员集中进行,耗时在15-25分钟,真正重要环节对号交接班一般只有5-10分钟,及在交接班的时段内,大部分时间无端消耗。
车站可将交接班环节进行改革,除点名与班前提问由值班主任完成外,将文电传达与重点事项强调划归至对号交接班的环节之内,并派驻专业管理人员对对号交接班进行全程盯控。将延长对号交接班时间,避免作业人员因时间问题被迫简化交接班流程的情况。
1.2 加强对交接班的现场控制
交接班环节无论如何优化,最终还是需要职工的严格执行,现阶段交接班环节基本无人能够自律执行相关要求,而管理人员在此阶段一般没有进行盯控的具体要求,造成交接班环节流于形式,交接纪律混乱。
因此现场管理资源向交接班进行倾斜,专业管理人员将对号交接的盯控作为日常工作的重点,充分利用视频监控,录音装置等远程监控手段,实现交接班在管控条件下进行。
1.3 优化交接班项点
交接班项点繁杂已是普遍现象,以哈密东站为例,车站值班员交接班项点多达15项,其中不乏卫生、备品和钥匙等与作业安全相关性较小的项点,优化哪些项点成文本文的主要研究对象。
2 交接班项点分析
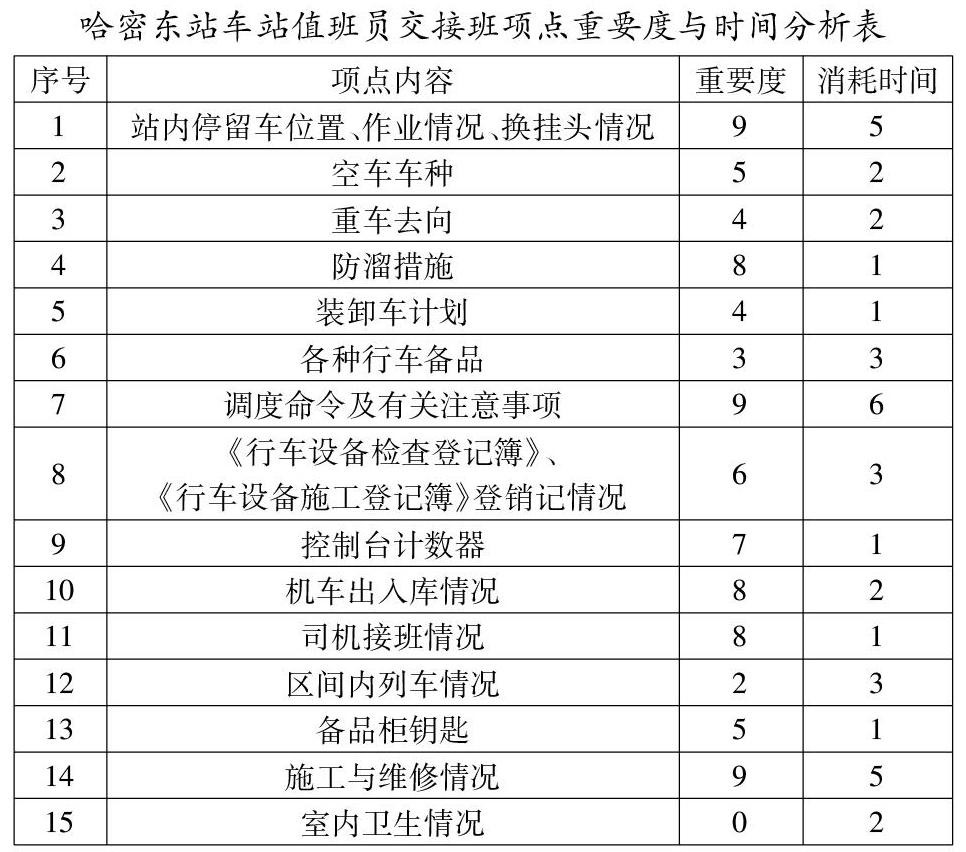
以哈密东站车站值班员交接班项点为例对其消耗时间及重要性进行分析。重要性权重赋值原则按照AHP层次分析法中专家打分的办法进行赋值:
(1)对于行车安全较其他项点有极端影响的赋值为9。
(2)对于行车安全较其他项点有强烈影响的赋值为7。
(3)对于行车安全较其他项点有较强影响的赋值为5。
(4)对于行车安全较其他项点有稍强影响的赋值为3。
(5)对于行车安全较其他项点有轻微影响的赋值为1。
(6)对于行车安全较其他项点没有影响的赋值为0。
相邻判断中间值:2,4,6,8。对于项点消耗时间,按照实际消耗时间统计,单位为分钟,将哈密东站对号交接项点按上述原则进行赋值,如下表所示。
如上表所示,16个交接项点总耗时为38分钟,而交接班时间一般需控制在30min之内。
3 利用动态规划进行求解
上文将交接班项点的消耗时间及重要度进行分析,可将问题转化成0-1背包问题,即项点时间为物品价值(W),项点耗时为物品重量(V),利用python3.7进行求解,具体结果将序号6(各种行车备品),12(区间内列车情况),15(室内卫生情况)三个项点剔除后消耗时间为30分钟,总价值下降值为5,价值总数符合预设目标。
4 结论
将哈密东站车站值班员交接班项点进行优化后,时间可缩短至30分钟以内,同时对于交接班安全影响较小,剔除项点与现场选择性未交接项点基本一致,利用此种办法对于现场车站值班员交接班优化具有一定的指导意义。
参考文献:
[1]孔德扬,广晓平,张红军.基于熵权模糊物元的客货混跑天窗模式优化[J].交通科技与经济,2012,14(6):28-31.
[2]孔德扬.铁路煤炭战略装车点布局规划研究[D].兰州交通大学,2013.
[3]郭风东,李涛.高速铁路调度指挥安全保障体系的探讨[J].铁道运输与经济,2011,9:28-30.

