高纵向应变下管道凹坑的评价方法

徐 婷，丁 飞，操建平 编译

（1.中国石油集团石油管工程技术研究院，西安710077；2.中国石油勘探开发研究院 石油工业标准化研究所，北京 100083）

0 引 言

管道施工建设和服役期间发生的外部干扰经常会导致管道产生凹坑。 此外，地面运动或其他异常情况可能使管道经受高纵向应变。 目前的凹坑评价方法是在假定主要载荷为内压且纵向应变水平较低的情况下，开发并进行验证的。 而凹坑在高纵向应变下的行为研究较少，需要制定评价方法。

对于通过现场检测工具以及现场开挖发现的凹坑，如何评价取决于凹坑的类型。 普通凹坑具有光滑的轮廓，没有凿痕或腐蚀异常等有害特征。 复杂的凹坑包括沟槽、 划痕、 焊缝或环焊缝，以及其他引起应力上升的凹坑。 对于普通凹坑，大多数评价方法以静载荷作用下的凹坑深度和凹坑应变为研究对象，采用现行规范和标准（如 US 49 CFR 192 和 195[1-2]、 ASME B31.4 和B31.8[3-4]、 CSA Z662[5]） 中规定的凹坑验收标准。全尺寸试验表明，在静态载荷作用下[6-8]，通过爆破失效，普通凹坑对管道的结构完整性未构成威胁，因此对普通凹坑的评价主要集中在循环载荷引起的疲劳失效，这是通过采用如API 579[9]或BMT[10-11]中各种凹坑疲劳评价方法进行的。 通过PHMSA （美国管道与危险材料安全管理局） 赞助的各种项目和联合工业项目[12-14]，制定了凹坑评价方法行业指南和推荐做法。

现有的凹坑评价模型大多没有考虑纵向应力和应变的影响，尤其还没有研究高纵向应变对疲劳寿命和抗压屈曲的影响。 对于抗压屈曲，大多数研究都集中在开发用于计算平端钢管或环焊缝钢管CSC （压缩应变能力） 的评价模型，如CSA Z662 （加拿大标准协会）、 DNV OS F101 （挪威船级社）[15]、 API RP 1111[16]、 UOA 模型[17]、 CRES（能源系统可靠性中心） 模型[18]。 近期主要研究了凹坑和材料应变硬化性能对管线管[19]抗压能力的影响。 然而，在文献[19]中评价的钢管是在纯轴向压缩下进行加载的，并不是在地面运动导致弯曲的情况下加载的，尚未研究含弯曲主导变形的普通凹坑管段的CSC。

普通凹坑对钢管CSC 的影响以及含凹坑钢管的CSC 评价方法是本研究的重点。 对于受高纵向应变作用的管段，凹坑附近的疲劳行为暂时不在本研究范围之内。

2 高纵向应变下管道凹坑的评价

2.1 CSC定义和计算

本研究将CSC 定义为有凹坑的钢管所能承受的与最大弯矩对应的压缩应变。 在达到最大弯矩并超过CSC 后，压缩应变会在管道的一小块区域内高度局域化，往往会形成褶皱。

本研究采用两种方法来计算CSC。 一种方法是计算局部2D CSC，它按照用于普通钢管的CSC 的传统定义，即在以褶皱处为中心的2D 测量长度范围内的平均压缩应变。 2D CSC 可能会受到褶皱处应变集中失稳的影响。 另一种方法是计算褶皱外的应变和推断褶皱处的应变，即整体CSC 或推断后的 CSC。 通过推断，CSC 的目的是反映凹坑钢管的整体能力，以适应整体/名义纵向弯曲变形。 下文中凹坑钢管的2D CSC 和推断CSC 用表示。

2.2 有限元分析

在施工过程中 （无内压） 或在服役中 （有内压） 可形成凹坑。 此外，凹坑会处于不同的限制条件下，即受限制的或不受限制的。 为了研究凹坑形成和限制条件对钢管CSC 的影响，采用有限元法模拟了不同的凹坑形成和限制条件，确定弯曲载荷下钢管的CSC。

使用有限元分析软件ABAQUS 进行分析。由于对称，仅对四分之一的钢管进行建模，模型采用四节点四边形壳单元简化积分法 （S4R）和大应变公式。 采用解析刚性表面 （ARSR） 对球面压头进行了数值模拟。 通过表面－表面接触模拟了压头与钢管的相互作用，钢管外径为323.85 mm，壁厚为 6.35 mm，径厚比为 51，压头直径为63.5 mm。 建模的钢管长度为10D，足以避免刚性钢管管端对凹坑附近应力/应变的影响，钢级为X65。

采用钢管生产企业质证书上给出的材料性能，建立了有限元的全应力－应变曲线 （SSC）。 屈服强度为471 MPa，极限抗拉强度为535 MPa。

对于施工过程中形成的无约束凹坑，需要5 个加载步骤来模拟凹坑的形成过程、 压力循环以及弯曲条件下的钢管变形。

5 个加载步骤为： ①在没有内部压力时，通过在钢管上产生凹坑，模拟凹坑的形成； ②移除压头，允许弹性复圆； ③模拟与静水压试验相关的压力循环； ④模拟运行过程中压力波动引起的压力循环； ⑤施加横向弯矩来模拟管道受压时由于地面运动而产生的弯曲载荷。 弯曲时，凹坑位于钢管的受压侧。

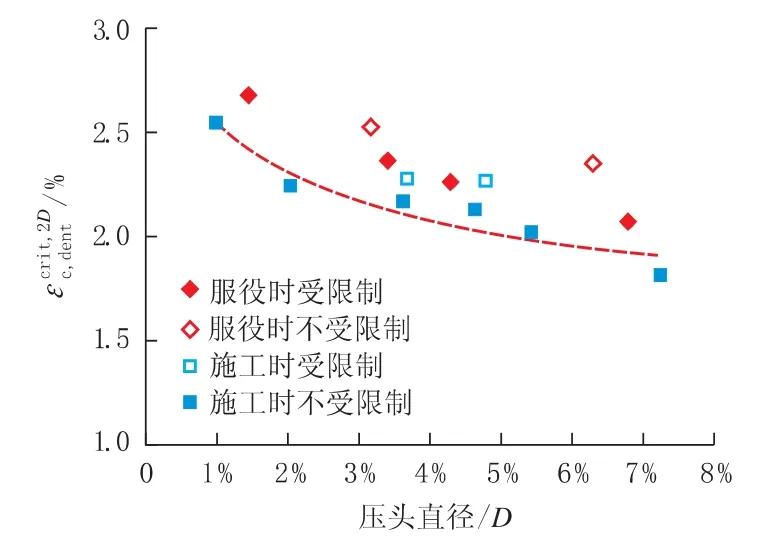
图1 不同凹坑形成和约束条件下凹坑钢管的2D CSC

2.3 全尺寸试验

采用C－FER 技术进行了全尺寸弯曲试验。共4 个试样，3 个试样包含凹坑，1 个未包含凹坑 （即普通钢管）。 试样从外径为324 mm、 壁厚为6.35 mm、 钢级为X65 的电阻焊管线管上制取。 采用直径63.5 mm 的钢球作为压头的伺服液压控制设施，在试件中部制作凹坑，如图2 所示。 零压力下，进行压痕和弹性复原后，制作的凹坑深度为 5.3 mm （1.6%D），13.6 mm （4.2%D）和 43.1 mm （13.3%D）。

图2 凹陷钢管和钢球压头示例

全尺寸弯曲试验在C－FER 设计的弯曲框架中进行，试验装置如图3 所示。 该设备为伺服液压控制加载系统，包括三个液压装置。 该系统能独立控制施加的弯矩和轴向力，并能自动补偿内部压力在试件端盖上产生的轴向力。

图3 全尺寸弯曲试验装置

试验测量项目包括顶、 底支板受力，试件内压，中跨挠度，试件旋转，试件在选定位置受拉伸和受压缩侧的轴向应变以及选定位置的环向应变。 在单轴/双轴应变仪的基础上，利用视觉图像关联三维成像系统绘制试件受压侧的表面应变图。

弯曲试验分两个加载阶段。 在第一个加载阶段，将带凹坑的试件加压至相当于90%SMYS的公称环形应力水平，以形成预期在使用前的水压试验中产生的凹坑的塑性复原。 然后，增加5 个压力循环，使最大环形应力水平达到72%SMYS，以稳定凹坑。 在第二加载阶段，压力保持在一个水平，产生72%SMYS 的环形应力水平，然后通过击打上、 下锤逐渐施加弯矩。 持续弯曲至试验设备达到变形极限，或直到试件由于压力容器的破坏而失效。 在增压过程中，施加外部轴向载荷来补偿压力引起的管端端帽上的力。

主要结果包括超过连接褶皱部位的规定测量长度的局部弯矩峰值和在弯矩峰值时的平均压缩应变 （即CSC）。 已知的平均压缩应变有两种计算方法： 第一种，使用侧拉伸应变计和测斜仪来确定，以试件中部为中心的1D 测量长度上的平均压缩应变，这里称为 1D 应变 （DI）； 第二种方法，利用压缩面图像的VIC （视觉图像关联）数据，确定以褶皱部位为中心的1D 和2D 测量长度上的平均压缩应变，这里称为1D 和2D 应变 （VIC）。 在文献[20]中第 3.2.5 条介绍了这些平均压缩应变的计算方法。

全尺寸弯曲试验关键的试验参数和结果见表1，这些数据包括凹坑深度、 局部弯矩峰值和得到的CSC。 从表1 可以看出，局部弯矩峰值和CSC 随着凹坑深度的增加而减小。 由VIC方法得到的CSC 的值，比由测斜仪和侧应变仪推断出的应变值更精确。 CSC 的值显示，凹坑深度从 0 增加到 2.7%D，导致 CSC 减少了约30%，局部弯矩峰值减少了约11%。 当凹坑深度继续增加到5.5%D 时，CSC 额外的减小值明显变小，与凹坑为 2.7%D 时相比，约 9%。 局部弯矩峰值未继续减少。

表1 全尺寸弯曲试验结果

局部弯矩和2D 应变 （VIC） 之间的关系如图4 所示。 当弯矩接近峰值且接近CSC 时，钢管内受压侧开始弯曲或形成褶皱。 然而，褶皱幅度在达到CSC 之前通常是非常小的。 达到CSC 后，弯矩开始下降，褶皱幅度逐渐增大，直至形成主褶皱 （紧挨着凹陷处）。 随着主褶皱的形成，次褶皱的幅值逐渐减小，在弯曲度增大的情况下，主褶皱幅值增长较快。 当试验设备达到弯曲旋转极限时，所有试验结束。 虽然在此阶段试验中的褶皱幅度非常显著，但是所有的试样都保持了压力完整性。 全尺寸试验中产生的向外褶皱如图5 所示，由图5 可见，4 种试样均在试样中点约48～63 mm 处产生了向外的褶皱。

图4 全尺寸弯曲试验中局部弯矩和2D 应变（VIC）对比

图5 全尺寸弯曲试验中产生的向外褶皱

2.4 有限元分析与试验结果对比

有限元分析和试验得到的凹坑深度对比如图6所示。 参数dde为弹性复原之后和压力循环之前的凹坑深度； dd0为压力循环引起的塑形复原之后和施加弯矩之前的凹坑深度，在无内压时测量凹坑深度。 由图6 可见，由有限元分析和试验得到的dd0和dde之间的关系趋势有着良好的一致性。 对于相同的dde，有限元分析计算得到的dd0略大于试验测得的dd0。

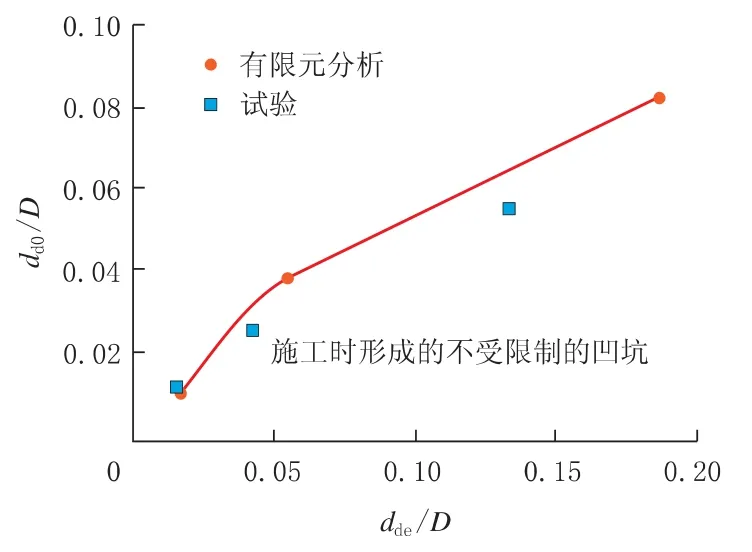
图6 有限元分析预测结果与试验得到的凹坑深度对比

有限元分析与试验得到的2D CSC 和凹坑深度的关系如图7 所示，有限元分析与试验得到的CSC 和凹坑深度的关系如图8 所示。

在图7 和图8 中，CSC 都以零内压下剩余凹坑深度 （dd0） 的函数来表示。 根据 FEA 预测和试验结果，CSC 和dd0之间关系的一般趋势显示出非常好的一致性。 然而，FEA 预测的CSC 始终低于试验结果 （约20%）。 预测和实测CSC 的差异被认为是由有限元分析中假定的钢管应力应变曲线 （SSC） 与小规模试验确定的钢管材料实际的应力应变曲线 （SSC） 之间的差异造成的。有限元分析与试验获得的SSC 对比如图9 所示。钢管在6 点钟的位置比在3 点钟的位置具有更高的强度。 在全尺寸试验中，焊缝位于中性轴附近，3 点钟位置的材料位于最外层受压纤维上，如图10 所示。 未被有限元分析识别的中性轴 （6点钟位置） 上较高强度的材料，可减少钢管的椭圆化和增加CSC。

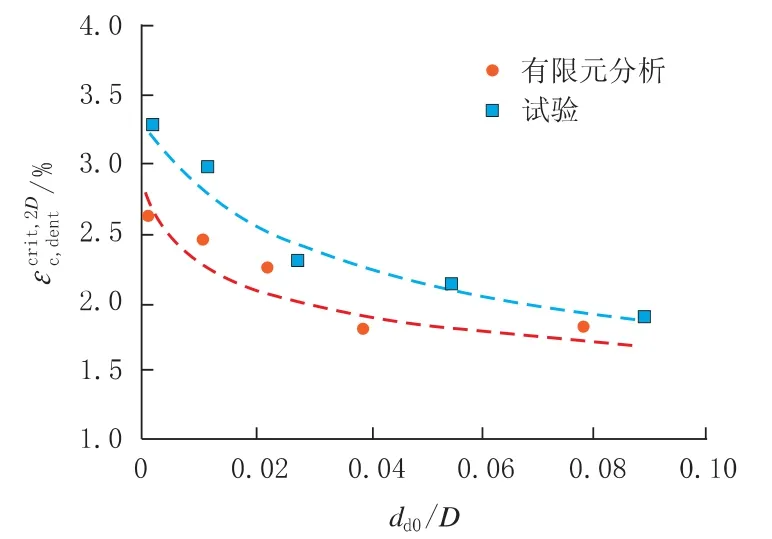
图7 有限元分析与试验得到的2D CSC 和凹坑深度

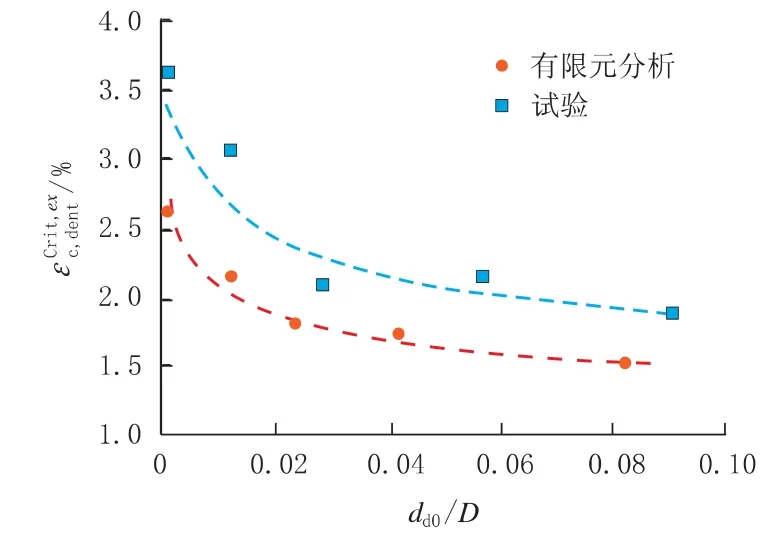
图8 有限元分析与试验得到的CSC 和凹坑深度

图9 有限元分析与试验获得的SSC 对比

图10 凹坑钢管全尺寸弯曲试验示意图

2.5 不同参数对凹坑钢管CSC的影响

参数化有限元用来检验钢管几何形状 （D/t=51 和 72）、 钢管材料应变硬化 （屈强比为 0.77和 0.88） 和内压 （fp=0 和 0.72） 对具有不同凹坑深度 （从 0 到 8%D） 的钢管的 CSC 的影响。 参数化FEA 的关键结果总结如下：

（1） CSC 随 D/t 比值和凹痕深度增加而降低。 D/t 比为 51，凹坑深度从 0 增加至 8%D时，CSC 逐渐减少。 D/t 比为 72，凹坑深度从 0增加至 1%D 时，CSC 快速减少。 一旦凹坑深度超过1%D，CSC 基本上不受凹坑深度进一步增加的影响。

（2） CSC 随屈强比和凹痕深度增加而降低，对于具有不同屈强比的两种钢管，随凹痕深度变化，CSC 的变化非常相似。 随着凹坑深度从0 增加至8%D 时，CSC 值逐渐减小。

（3） CSC 随着凹坑深度的增加和内压的减小而减小。 加压时，随着凹坑深度从0 增加至8%D，CSC 值逐渐减小。 在非加压条件下，凹坑深度从 0 增加至 1%D 时，CSC 快速减小。 一旦凹坑深度超过1%D，CSC 基本上不受凹坑深度进一步增加的影响。 在非加压条件下，由于凹坑的存在，CSC 的降低比加压条件下要高。

2.6 凹坑钢管评价的CSC方程

文献[18]中普通钢管的CSC 方程作为钢管几何缺陷的函数给出。 本研究将凹坑作为一种等效几何缺陷，采用附加方程的形式建立了带凹坑钢管的CSC 方程。 首先，采用普通钢管的CSC 方程反推计算等效几何缺陷，此等效几何缺陷导致了由参数化有限元分析得到的带凹坑钢管的然后，在如凹坑深度、 D/t 和屈强比等不同参数下，绘制了等效几何缺欠图。最后，通过曲线拟合确定等效几何缺陷与上述参数之间的关系。 结果表明，对于既定的凹坑，等效几何缺欠很大程度上受钢管D/t 的影响，而不是屈强比。 几何缺陷，以凹坑标准等效几何缺欠高度形式出现，与标准凹坑深度 （ddp/D） 和钢管 D/t 的函数相吻合，由下式进行计算

其中，ddp/D，D/t 和的单位均为 mm/mm。

2.7 凹坑钢管的CSC评价准则

准则包括两种不同级别的评价程序。 一级程序由易于使用的方程组成，二级程序涉及具体个案的有限元分析。 如果一级程序不适用，或评价结果被认为限制性太强，可以使用二级程序。 本研究仅涉及一级评价程序，二级评价程序见文献[21]。

2.7.1 确定一级评价中的输入参数

采用下列步骤确定一级评价中的输入参数：

（1） 确定钢管的工称直径和壁厚。

（2） 确定工作压力 （pi），正常操作时，应采用下限压力。

（3） 确定钢管屈强比 RYT（Y/T）。 应采用纵向上限屈强比。

（4） 确定钢管屈服强度 （σy），应采用上限钢管屈服强度。

（5） 确定加压条件下凹坑深度 （ddp），应采用预期的下限内压下的最大凹坑深度。 如果凹坑深度是在内压高于被测的下限压力的情况下测量的，凹坑深度应修正 （通常是通过在下限内压下得到一个较大的凹坑深度来增加凹坑深度）； 如果在零压下测量凹坑深度，在加压条件下，可采用API 579 中12.3.3.1 条文献[9]中的程序和方程来确定凹坑深度。

（6） 计算标准凹坑深度 （ddp/D）。

（7） 计算压力系数 fp=piD/（2tσy）。

（8） 确定一级评价的适用范围。 如符合下列适用范围及文献[18]中的CSC 方程的适用范围，便可进行一级评价。 如不符合以下适用范围或文献[18]中的CSC 方程的适用范围，则进行二级评价。 一级评价适用范围：

51≤D/t≤72；

0.77≤Y/t≤0.88；

0.72≤fp≤0.80；

0≤ddp/D≤0.08。

2.7.2 评价程序和CSC 方程

可采用下列步骤进行一级评价：

（2） 用文献[18]中给出的 CSC 方程计算无安全系数的用步骤1 中计算的标准等效几何缺欠高度代替标准几何缺欠高度

其中，γc为用于 CSC 的安全系数，推荐 γc≤0.8。由上述方程计算得到的参数为百分数。 例如，若 CSC 为 2.0% （即 0.02 mm/mm 或0.02 in/in），计算得到的为2.0。

2.7.3 准则适用性的注意事项

以上评价程序及CSC 公式适用于： 带普通凹坑的钢管； 在施工或使用过程中形成的受约束或不受约束的普通凹坑； 承受位移控制的纵向载荷的管段； 承受载荷控制的纵向载荷 （如自由跨度） 的管段，并使用基于应力的准则[22]对塑性挤毁进行额外的检查； 处于弯曲控制变形下的管段。 本方法不适用于承受纯轴向压缩的管段。

钢管抗压屈曲敏感性通常通过比较CSC （即阻力） 与应变需求 （即载荷） 来评价。 应变需求的定义和计算应与应变能力一致。 建议局部与包含褶皱附近的本地区域应变估计的应变需求一起使用。 例如，使用类似2D 的测量长度的惯性测量单位 （IMU） 工具测量的应变。 当IMU 测量长度大于2D 或应变需求由有限元法确定时，采用横臂式钢管模型。 推荐使用因为未发现由于褶皱引起的集中应变。

3 结 论

本研究涵盖了PHMSA 资助项目的研究结果，该项目旨在研究同时承受高纵向应变的异常钢管 （包含异常腐蚀、 凹坑和褶皱） 的评价程序。 通过有限元分析和全尺寸弯曲试验，研究了凹坑钢管CSC 的评价准则。

（1） 钢管的CSC 在纯凹坑存在时趋于减小。在施工过程中形成的无约束纯凹坑在CSC 中减少量最多。 在评价的条件下最大减少量约为 30%，最大减少量约为 40%。

（2） CSC 随着凹坑深度、 D/t 和屈强比的增加而减少。 对具有D/t 的钢管，随着凹坑深度的增加，CSC 迅速下降，最终达到一个平台，之后凹坑深度的进一步增加对CSC 的影响不显著。

（3） 在非加压条件下，由凹坑引起的CSC的减少比加压条件下要高。

（4） 所编制的准则可用于高纵向应变下，带纯凹坑的服役钢管的CSC 评价。