基于概率分析的核电传热管降质失效评估方法研究
陶于春, 任尚坤,彭志珍, 温俊鸽
(1.苏州热工研究院有限公司 深圳分公司,深圳518124;2.南昌航空大学 无损检测技术教育部重点实验室,南昌330063)
研发清洁能源和发展核能是国家能源安全的重大战略。 核安全是核电可持续发展的前提,是广大公众对核电技术发展的基本要求[1-3]。 核电传热管是核电安全的脆弱环节,对传热管的安全评价研究直接影响到整个核电机组的安全性[4-6]。 核电厂的重大事故多与传热管的泄漏、 破裂有关[7-8]。刘云[9]等开展了传热管胀管过渡段的超声无损检测技术研究,探索了常规涡流检查技术在传热管的胀管过渡段存在的检测问题[10]。
采用标准 GB/T 15260—1994 的方法,林震霞[11]等对蒸汽发生器690 合金传热管进行了晶间腐蚀试验,采用沸腾硝酸溶液和沸腾硫酸-硫酸铁溶液作为腐蚀介质,得到了晶间腐蚀速率的重要数据。 目前国内二代压水堆核电机组的蒸汽发生器在弯管区大都设置了防振条组件,用于支撑SG 弯管区的传热管,抑制运行期间管束的流致振动,以保证传热管在寿命期内的完整性。 但是,防振条对传热管的完整性也存在一定的影响。 崔素文[12]等研究了防振条的振动对传热管损伤的影响。 研究发现,防振条自身的问题对传热管的安全性有较大影响。 在蒸汽发生器传热管二次侧,横向流动的流体存在明显的激励和振动,具有固有的频率和振型,严重影响传热管的安全性,也是分析评价的关键因素[13-14]。 施少波等[15]利用ANSYS 有限元法对传热管的滚压堵头进行了仿真分析和评定,得到了具有一定意义的结果。
目前,对于传热管的降质评估研究较少见,本研究基于概率论理念,对蒸汽发生器传热管的安全性进行概率评估研究,期望能对核电系统的高效运行和安全生产提供借鉴。
1 核电传热管降质影响因素分析
引起核电站传热管降质的因素很多, 主要包括: 应力腐蚀、 高周疲劳、 微振磨损、 晶间腐蚀、化学腐蚀。 不同的降质机理,产生复杂多样的破损形式。 有些降质机理对传热管的影响相互独立,有些对传热管的影响相互联系和相互叠加。
(1) 应力腐蚀。 应力腐蚀是应力和腐蚀物质共同作用而产生的腐蚀,比纯粹的应力腐蚀破坏性更严重。 主要与高温腐蚀环境、 高残余应力和工作应力、 材料微观结构有关。 应力腐蚀是一次侧和二次侧区域重要的降质因素,在管体的弯头处、 胀管区、 凹痕处最易发生应力腐蚀。 当应力达到或接近屈服强度时,材料的腐蚀状况会迅速恶化。
(2) 高周疲劳。 高周疲劳是在长期周期性变化载荷作用下的一种降质过程。 在U 形弯管区和管板上表面最容易发生高周疲劳损伤。
(3) 微振机械磨损。 核电机组在运行过程中,传热管不可避免地会发生振动,防振条和支撑板的碰撞或切向滑动是微振机械摩损的主要原因。
(4) 晶间腐蚀。 晶间腐蚀是发生在传热管材料表面晶粒边界的相对均匀的腐蚀。 因为在管体壁上不可避免会积聚腐蚀物,导致管壁均匀减薄,从而应力增加加速生成裂纹,导致爆管。
(5) 化学腐蚀。 化学腐蚀是由于在二次侧水化学处理中,存在一些腐蚀性的化合物产生的。 化学腐蚀的表现是传热管外壁均匀减薄,最终加速生成裂纹,导致爆管。
2 基于Bayes分析的传热管降质失效的概率评估方法
2.1 传热管降质失效概率评估模型
2.1.1 先验分布和样本信息的确定
设A3表示失效堵管事件,P(A3)表示失效堵管事件的概率; A2表示降质达到预警临界值的事件,P(A2)表示预警管子事件的概率; A1表示传热管处于正常事件,P(A1)表示传热管处于正常事件的概率。 根据概率理论,由 A1、 A2、 A3基本事件组成完备的样本空间,Ω={A1,A2,A3},P(A1)+P(A2)+P(A3)=1。
在失效概率评估中,确定 P(A3)、 P(A2)、 P(A1)的先验分布通常有两种方式: ①历史检测数据法,P(A3)、 P(A2)、 P(A1)先验分布可基于历史记载的数据通过分析可获得; ②专家主观概率法,主观概率并不是没有根据的胡乱设定,是根据专家对事件的认识做出的切合实际的判断。 虽然具有主观性,但又是综合各方面知识积累和实践经验,对客观事物的发展规律进行推理、 综合判断而设定,有时比客观数据更可靠。 可作为主观概率先验分布。
在实践中,由于导致传热管降质的因素很多,先验分布无论来自主观数据或是客观数据,都不能作为未来降质失效堵管的可靠概率,都要在新的条件下进行重新评估。 因为各个影响因素的实际情况会时常发生变化,其内部构成及分布具有不确定的变化规律,各种事件的概率分布也会随之发生变化。 例如,核电站的满负荷运行、 半满负荷运行或者停机,降质因素的内部构成就不同。
假设使事件Ai降质的因素为B,B 可以分为 j 类,表示为 Bj。 第 j 类影响因素所占的权重比例为P(Bj)。 则发生事件 Ai后,Bj影响因素的权重分布为P(Bj/Ai)。 由于通过数理分析获得的条件概率P(Bj/Ai)要比获得条件概率P (Ai/Bj)容易。 所以先通过数理统计获得条件概率P(Ai/Bj),再通过Bayes公式求得P(Ai/Bj)。
2.1.2 影响因素的修正
首先讨论单影响因子的修正。 根据检测记录和专家数据获得P(Ai)先验分布和样本信息P(Bj/Ai)后,依据Bayes 定理对数据进行修正,可获得后验分布。 即可由Bayes 公式(1)获得影响因素B对堵管事件评估的后验概率。
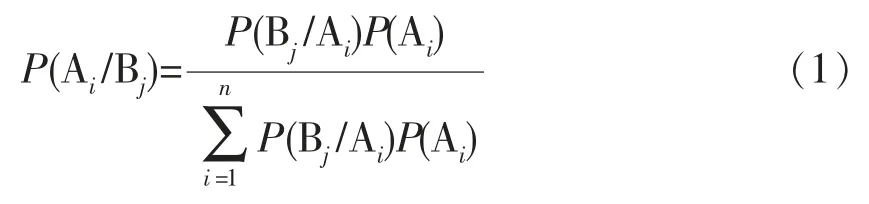
依据修正后的后验概率,结合影响因素各个类别的权重比例,利用全概率公式(2),便可得到考虑影响因素内部变化修正后的发生概率。
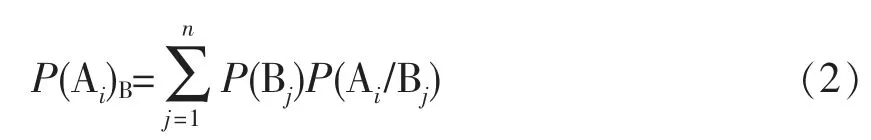
对于多影响因子的修正,可依次对每一项因素进行类似操作,对每一项影响因素逐一修正。当有多个影响因素需对概率进行修正时,假设各个影响因素是独立的,概率计算步骤如下。
第一步: 根据历史检测数据或专家数据,确定先验分布P(Ai)。 如可根据降质损伤程度确定P(A1)、 P(A2)、 P(A3)的权重值。
第二步: 对确定的影响因素进行分类,如影响因素 B、 C、 D 等。
第三步: 确定每种影响因素的特征、 每种影响因素的级别,以及不同级别所占的权重比例。如影响因素 B 类可分为 B1、 B2、 B3,即是影响严重、 影响中等、 影响轻微三个级别。 如可设定所占权重比例为P(B1)=0.4、 P(B2)=0.3、 P(B3)=0.3 等。P(B1)+P(B2)+P(B3)=1。
第四步: 根据以往记录的检测数据进行数理分析,得到某影响因素 (例如B) 下的样本信息P(Bj/Ai)。
第五步: 采用Bayes 公式计算影响因素B 的后验概率P(Ai/Bj)。
第六步: 采用全概率公式计算影响因素B的修正概率。
第七步: 以影响因素B 的修正概率值为基础,进而依次计算其它影响因素的修正概率。
2.2 案例分析
应用提出的概率论模型计算传热管降质失效概率问题的案例分析如下。 在现实实践中,通过对导致传热管降质的各影响因素分析,设影响因素可归结为两种,一是应力腐蚀因素B,包括晶间腐蚀和化学腐蚀,二是疲劳振动损伤因素C。 认为应力腐蚀和疲劳振动损伤是两个独立损伤事件。 以下首先分析应力腐蚀产生的管体失效分布状况。
将传热管降质事件设为A,A1表示管体处于正常事件,P(A1)表示管体处于正常事件的概率;A2表示降质达到预警临界值事件,P(A2)表示预警管体事件的概率; A3表示失效需堵管事件,P(A3)表示失效需堵管事件的概率。 则P(A1)+P(A2)+P(A3)=1。
步骤一: 根据历史数据统计或专家给出的主观数据,确定概率先验分布。 如记录的100 000 个检测传热管中,有10 个失效管,50 个预警管,其余为正常管,则可得到P(A1)=0.999 4, P(A2)=0.000 5,P(A3)=0.000 1。
步骤二: 根据历史数据统计或专家给出的主观数据,确定影响因素B 的权重值P(B)。 影响因素应力腐蚀B 和疲劳振动损伤C 的取值及表示含义和构成比例见表1。 根据应力腐蚀的程度和疲劳振动损伤的程度对影响因素所处状态的权重进行赋值。 P(B1)=0.4,P(B2)=0.3,P(B3)=0.3。 说明在历史检测的传热管中,有40%处于严重腐蚀状态、 有30%处于一般腐蚀状态、 有30%处于轻微腐蚀状态。 如果核电运行状态和环境有所变化,应对表1 权重分布状况进行调整。

表1 传热管降质失效影响因素的分布状态、 权重取值及表示的含义
步骤三: 根据历史检测数据的统计,或专家数据进行抽样。 通过数理统计,得到传热管三种状态事件发生时,关于影响因素分布的权重信息P(Bj/Ai),见表2 和表 3。 表2 表示应力腐蚀产生的样本信息P(Bj/Ai)分布,表3 表示振动疲劳磨损产生的样本信息P(Cj/Ai)分布。
步骤四: 采用 Bayes 公式(1)计算影响因素 B 和C 的后验概率P(A/B)和P(A/C),结果见表 4 和表 5。设P(A1)=0.999 4,P(A2)=0.000 5,P(A3)=0.000 1。
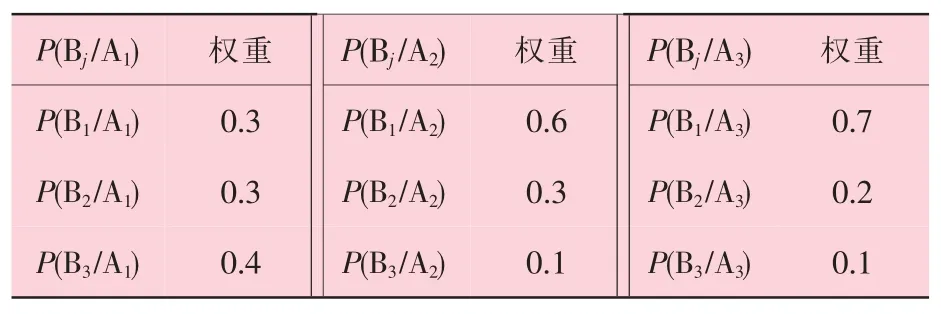
表2 应力腐蚀影响因素下的样本信息及其权重
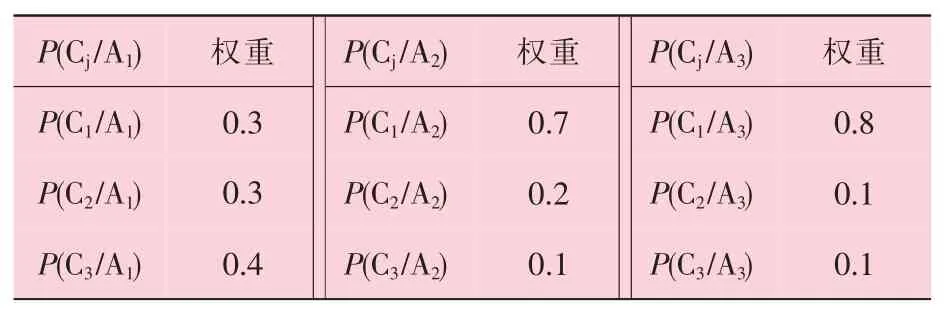
表3 疲劳振动损伤影响因素下的样本信息及其权重
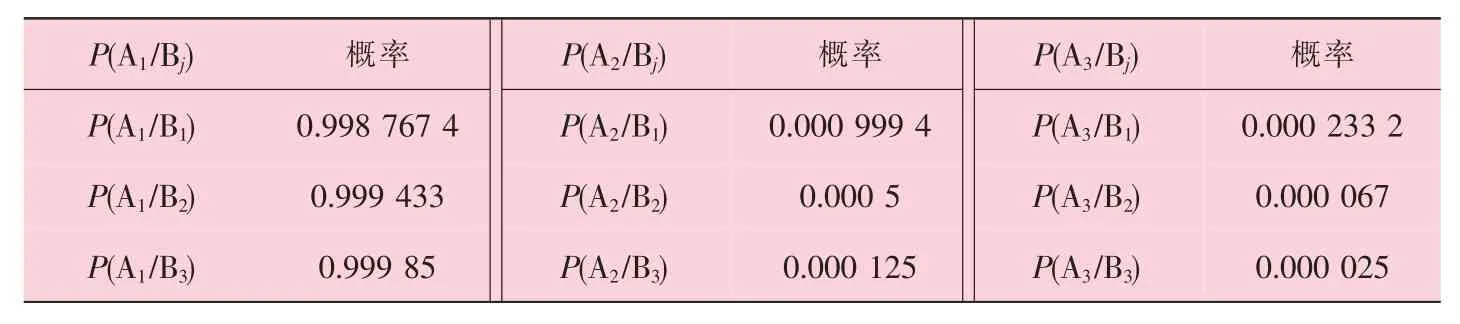
表4 应力腐蚀影响因素的后验概率分布
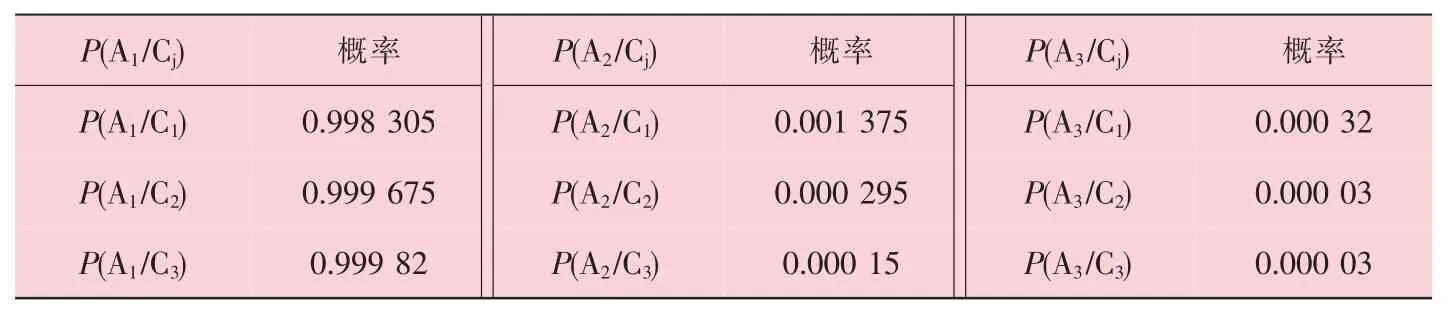
表5 疲劳振动损伤影响因素的后验概率分布
步骤五: 采用全概率公式(2)计算影响因素B的修正概率。 可得P(A1)B=0.999 29、 P(A2)B=0.000 59、P(A3)B=0.000 12。 即得到了经过影响因素B 修正之后的概率。
如果应力腐蚀严重,权重值修改为P(B1)=1、P(B2)=0、 P(B3)=0,经过影响因素B 修正之后的概率为 P(A1)B=0.998 7674、P(A2)B=0.000 999 4、 P(A3)B=0.000 233 2。 可见失效需堵管概率上升为1.94 倍(0.000 233 2/0.000 12=1.94),预警率上升为 1.7 倍。
如果应力腐蚀为轻微,权重值可修改为P(B1)=0、 P(B2)=0、 P(B3)=1,经过影响因素 B 修正之后的概率变为P(A1)B=0.999 85、 P(A2)B=0.000 125、P(A3)B=0.000 025。 失效需堵管率降低为0.21 倍(0.000 025/0.000 12=0.21),预警率降低为 0.21倍。 可见,腐蚀状态和疲劳损伤状况改变,失效堵管率会明显发生变化。
可见,由于应力腐蚀因素的影响,腐蚀严重和腐蚀轻微情况相比,管子的失效概率改变量将达到 9.24 倍 (1.94/0.21=9.24)。 即是如果上个检测周期系统是在轻微腐蚀的状态下运行,检测时管子的失效概率为η; 如果当前检测周期系统是在严重腐蚀的状态下运行,管子的失效概率将可达到9.6η。
步骤六: 以 P(A)B为基础,采用 Bayes 公式(1),计算影响因素C 的后验概率。 其后验概率P(A1/C)见表5。
步骤七: 采用全概率公式(2)计算影响因素C的修正概率。 可得到P(A1)BC=0.999 17、 P(A2)BC=0.000 684、 P(A3)BC=0.000 146。 又得到了经过影响C 因素修正之后的概率。 即可得到经过影响因素B 和C 修正之后的概率。
如果疲劳损伤严重,权重值修改为P(C1)=1、P(C2)=0、 P(C3)=0,可得到P(A1)BC=0.998 305、 P(A2)BC=0.001 375、P(A3)BC=0.000 32。 可见,如果疲劳损伤严重,失效需堵管率将上升为2.13 倍 (0.000 32/0.000 15=2.13),预警率上升为 1.93 倍。
如果疲劳损伤为轻微,权重值修改为P(C1)=0、P(C2)=0、 P(C3)=1,可得到 P(A1)BC=0.999 826、 P(A2)BC=0.000 15、 P(A3)BC=0.000 03。 可见,如果疲劳损伤轻微,失效需堵管率将降低为0.2 倍 (0.000 03/0.000 146=0.2),预警率降低为 0.21 倍。
可见,由于疲劳损伤因素的影响,疲劳严重和疲劳轻微,将导致管子的失效概率改变达到2.13/0.2=10.65 倍。 同时考虑应力腐蚀因素和疲劳损伤因素的共同影响,管子所处环境降质严重和降质轻微的不同,将导致管子的失效概率差值达到 9.246×10.65=98.4 倍。
3 结束语
本研究基于全概率概念和Bayes 理论,分析建立了核电传热管降质失效概率的评估方法。Bayes 公式和全概率概念相结合,解决了多个影响因素作用的复杂问题,Bayes 公式主要起到标定作用,全概率公式解决具体管子失效的概率问题,简化了计算方法。 该模型可以针对多个具体的降质因素进行逐一修正,该方法的特点是更灵活和方便,根据实际损伤因素和损伤程度随时调整损伤因素权重比例,可得到较准确的评估结果。 对于单一影响因素,损伤严重和损伤轻微,将导致管子的失效概率改变大约10 倍,即是由于单一因素的影响,设管子失效的最小概率为η,则管子失效的最大概率可达到10η; 如果考虑两种影响因素共同作用,两种因素损伤严重和损伤轻微,设管子失效的最小概率为η,则管子失效的最大概率可达到100η。 可见,检测灵敏度是可信的,可以进一步计算降质严重程度不同层次的概率。 该研究方法能够针对不同的影响因素,以数理方法为手段,可明显消除人为主观对评估结果的不利影响,具有很强的可操作性。 下一步的工作是进行大量的试验和数据信息的搜集,验证并提高该评价方法的准确性,下一步减小评价误差。

