中高轨航天器月影下能量平衡计算方法
崔波 孙世卓 陈世杰
(1 北京空间飞行器总体设计部,北京 100094)(2 中国空间技术研究院通信卫星事业部,北京 100094)
对于使用锂离子蓄电池组作为储能装置的中高轨航天器而言,全年有大部分时间处于长光照期,其电池处于搁置状态。与氢镍蓄电池组在长光照期始终保持满荷电态不同,锂离子蓄电池组为了降低搁置期的容量衰降,通常都采用低温半荷电态进行搁置,在进入地影季之际再调整至正常工作温度并充满电。
航天器在轨运行时会进入月影[1],其间太阳电池阵供电功率下降,电源转入联合供电状态或完全由蓄电池组供电。月影发生的时间不像地影那样相对固定,对于采用锂离子蓄电池组,长光照期电池处于低温半荷电态搁置的航天器[2]而言,存在蓄电池组过放甚至航天器掉电的风险[3]。相比地影,月影的出现时间不固定,且半影时间较长,要想精确的对月影期间电源工作情况进行计算以支撑蓄电池组在轨管理的相关决策,就需要对月影的发生时间、光照强度进行预测,结合预测结果计算太阳电池阵输出功率,进而计算蓄电池可能的放电深度。目前,相关研究大多关注航天器月影的预报方法[4-5],未结合能量平衡计算方法进行预测,指导意义不强。
本文提出了一种月影预测与能量平衡动态计算方法,对月影时间及月影时的光照强度进行计算,结合太阳电池的地面测试数据,计算整个月影过程中的太阳电池阵的输出功率。采用航天器太阳电池阵-蓄电池组能量平衡计算模型,对月影下能量平衡状态进行仿真,并与在轨的实际情况进行了比对。
1 光照因子的计算
要计算月影发生的时间及发生时的被遮挡的程度,就需要获取月球、太阳的位置。关于太阳和月球的位置计算,已经有非常成熟的方法,本文中采用了美国喷气推进实验室(JPL)发布的展开历表[4]完成月球和太阳位置的计算,使用的具体版本为2008年2月建立的DE421版本[6-7]。
在航天器位置计算方面,本文采用了SGP4模型[8]计算航天器的位置,相应的航天器的两行根数(Two Line Element)通过公开数据库获取。
在获取了航天器、月球、太阳位置后,统一转换至J2000坐标系,以航天器为中心获取月球、太阳的半张角及月球与太阳之间的角距,当月球与太阳间的角距小于月球太阳的视半径之和时即会发生月影。通过上述角度还可以计算太阳被遮挡的面积。具体过程如下。
设航天器A的位置为[xA,yA,zA]T,太阳位置为[xS,yS,zS]T,月球位置为[xL,yL,zL]T,则以航天器为中心,太阳的半张角ωS为
(1)
式中:RS为太阳的半径。 以航天器为中心月球的半张角ωL为
(2)
式中:RL为月球的半径。
以航天器为中心,太阳和月球的角距θSL为
(3)
当θSL<ωL+ωS且θSL>ωL-ωS时,月影为半影;当θSL<ωL-ωS时,月影为全影。
由于太阳距离较远,ωS的变化范围不大,以地球中心点观测全年的变化范围在15.7″~16.3″内;从地心观测月球的半张角变化范围约为14.7″~16.7″范围内,再加上航天器本身的运动,月球半张角的变化较上述范围更大。当月球的半张角小于太阳的半张角时,月影只会有半影;当月球的半张角大于太阳半张角时,只要满足了θSL<(ωL-ωS)的条件,就会出现全影。
当出现月影时,以航天器为起点观测太阳,太阳部分被遮挡(见图1),假设太阳是个亮度均匀的圆盘,计算相应的被遮挡的百分比,计算过程如下。

注:S为太阳的中心,L为月球的中心。
通过余弦定理计算α和β为
(4)
(5)
太阳被遮挡区中,区域ABD的面积等于α对应扇形的面积减去ΔABS的面积为
(6)
同理,区域ABC的面积为
(7)
被遮挡区域上下对称,最终的太阳遮挡后的光照因子F为
(8)
2 月影情况下太阳电池阵输出功率计算
2.1 日地距离的影响
考虑太阳为光照强度恒定的点光源,忽略卫星位置变化导致的距离变化,地球轨道的光照强度与日地距离的平方成反比。在进行月影预测时,若当前的太阳电池阵输出功率为P1,当前的日地距离为r1,日地平均距离为r0,则在日地平均距离光照条件下的输出功率为
(9)
日地距离在冬至前后达到最小值,其光照强度与全年平均值的比值在1.03左右;日地距离在夏至附近达到最大值,其光照强度与全年平均值的比值在0.97左右。如果对计算的精度要求不高,可忽略其影响。
2.2 月影过程中温度的影响
月影与地影相比,通常半影时间较长。较长时间的半影状态下,除了由于光照强度下降导致的工作电流下降外,太阳电池阵温度的变化也会对工作电流产生影响。以某卫星使用的28%效率的三结砷化镓太阳电池片为例,其电池片的典型参数见表1。

表1 三结砷化镓太阳电池片典型参数
注:AM0为Air Mass zero的缩写,表示日地平均距离处地球大气层外的太阳辐射量。
以AM0状态为基准计算,考虑工作点始终维持在恒流段,仅考虑电流变化。若温度变化30 ℃,电流变化不到2%(电流系数取0.01,工作电流取值16.8 mA/cm2)。在半影区内,温度的下降会导致电池片输出电流的下降,但与太阳被遮挡的影响相比,温度的影响因素贡献较小,在进行能量平衡计算时可以忽略或简单的采用等效因子进行折算。
2.3 光照强度与输出功率的拟合
月影由于其半影时间长,弱光条件下太阳电池阵的输出功率与光照强度间并不是线性关系,因此要精确的计算月影期间的功率平衡情况,就需要建立弱光条件下的太阳输出功率与光照强度间的对应关系。本文通过参考地面试验测试结果进行拟合的方式,建立了上述关系。
地面试验时,采用了偏转测试件使用不同的光照角度模拟光照强度变化的方法。图2为针对某型三结砷化镓太阳电池片开展的AM0条件不同光照角度输出特性曲线测试的结果,测试以光线与电池片法线夹角0°~85°,每组间隔5°开展了18组测试。

图2 不同光照角度下的三结砷化镓电池片输出特性曲线Fig.2 Output characteristics of triple junctionsolar cells under different illumination angles
图2中,曲线自上而下依次对应0°至85°的18个不同测试角度。从图2可以看出,在光照角变化时,输出电流随着光照强度变化而变化,相对的电池片输出电压受影响比较小,而针对卫星上典型的恒压直流电源系统,太阳电池阵通常都工作在恒定的电压点(即母线电压加上通路压降),在光照强度变化时单片的工作电压点始终不变。
以某卫星为例,其母线电压为42 V,考虑线路压降4 V,电池片串联数为28片,则单片的工作电压为(42 V+4 V)/28=1.643 V。从图2可以看到,即便是光照强度0.087(85°)时,电池片仍然会工作在恒流输出段。
因此,在通常情况下可以认为不同光照条件下输出功率的比值就等于该光照条件下短路电流的比值。以短路电流的变化值作为功率变化的比值,拟合曲线见图3。
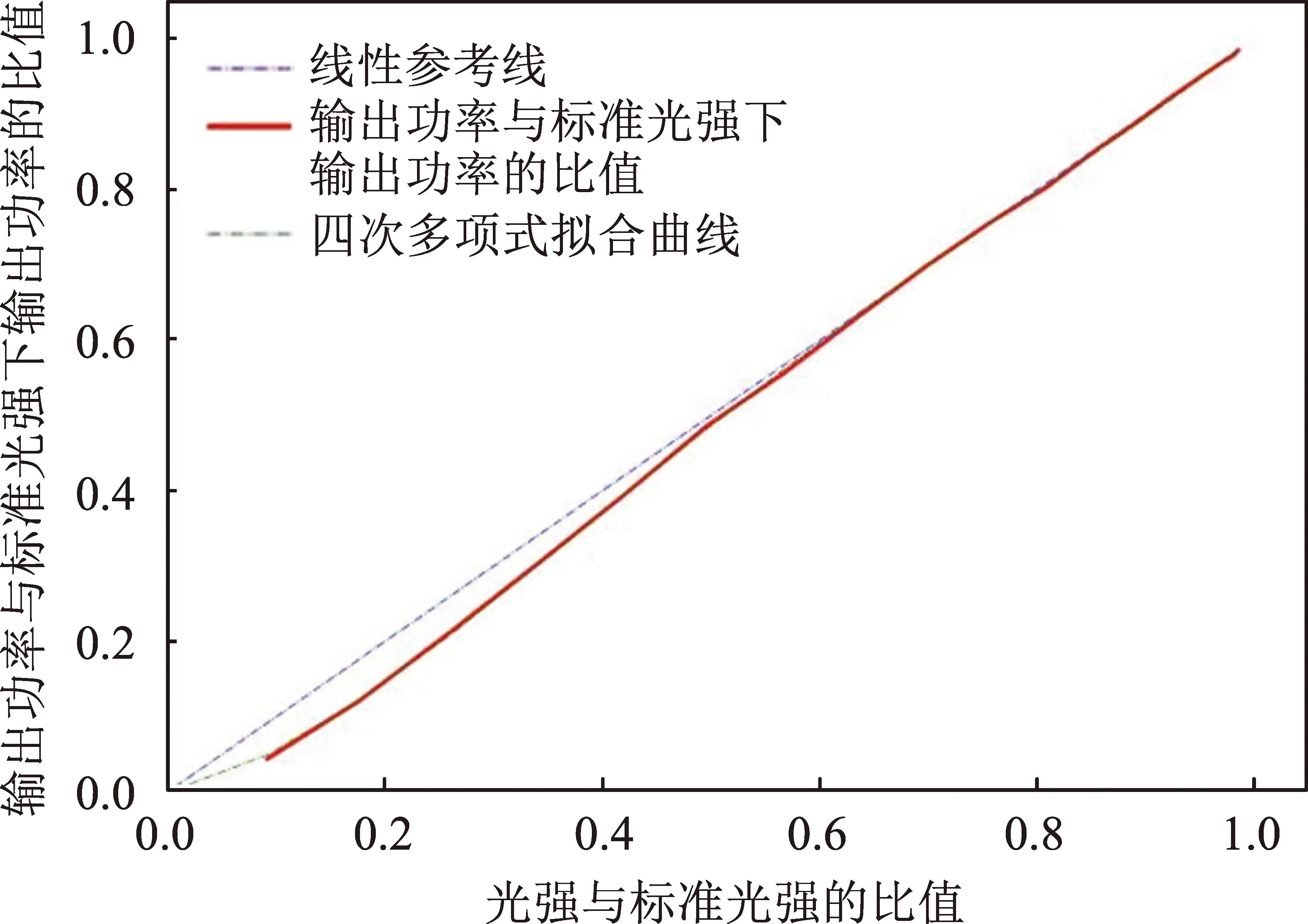
图3 不同光照强度输出功率与标准光强时输出功率的比值Fig.3 Ratio of output power to AM0
从图3可以看出,在光照强度比值0.6以上时,输出功率与光照强度能够保持较好的线性关系;在弱光条件下输出功率曲线会偏离线性参考线。通过多项式拟合,遮挡情况下太阳电池阵的功率输出值Px与发生遮挡时的光照强度因子x之间的关系为
Px=P0(1.364 377 95x4-3.262 254 41x3+2.557 863 25x2+0.344 742 38x-0.003 612 06)
(10)

3 能量平衡仿真模型
本文以中高轨航天器广泛采用的顺序开关分流调节(S3R)拓扑[9-10]为例,建立系统模型,结合太阳电池阵输出功率、母线负载、蓄电池组容量及初始荷电状态分析整个月影过程中电源的工作情况。构建电源分系统的仿真模型如图4所示。

图4 电源分系统仿真模型Fig.4 Electrical power system simulation model
仿真模型根据母线电容阵参数,结合分流调节器(S3R)、放电调节器(BDR)的输入电流及母线向负载模块和充电调节器(BCR)的输出电流,实时计算母线电压。通过母线电压与参考电压值的比例积分(PI)计算产生母线的主误差信号(MEA)。主误差信号控制分流调节器、放电调节器、充电调节器的工作状态。在充电调节器模块中,根据MEA值、蓄电池组电压、恒压充电设置值,共同计算充电电流大小及母线输入电流大小;在锂离子蓄电池组模块,参考地面试验数据(包含典型充放电曲线、内阻等)建立电池组模型[11],根据充电电流、放电电流大小及荷电态初始值,计算蓄电池组的当前荷电态及端口电压。
4 计算结果与在轨实际情况对比
某卫星在2018年7月13日8:02~8:34(UTC时间)经历月影,采用文章所述月影条件下太阳电池阵输出功率计算方法,以5月13日发布的两行根数参数进行预测计算,得到月影期间及月影前后的太阳电池阵输出功率计算值,与7月13日实际经历月影时的遥测数据进行对比,如图5所示。可以看出,计算结果与遥测数据高度吻合,证明本文的方法可以准确的预报月影对太阳电池阵输出功率的影响。仿真计算中,负载电流、太阳电池阵输出电流、蓄电池组搁置期间电压等数值按卫星在轨典型值计算,负载电流为42.5 A,太阳电池阵输出电流双翼108.4 A,蓄电池组电压为34.72 V。
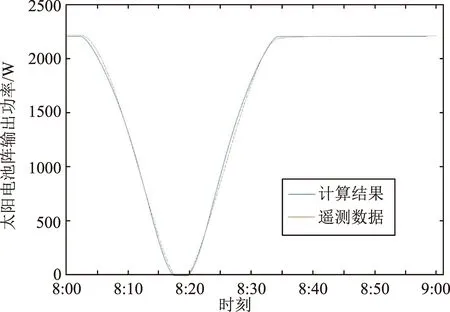
图5 计算太阳阵输出功率与遥测数据对比Fig.5 Comparison of telemetry data and calculated power of solar array
采用月影期间太阳电池阵输出功率计算结果以及能量平衡动态仿真方法,以该卫星在轨的平均负载作为输入,仿真蓄电池组在月影期间的工作状态,并与卫星在轨经历月影时的遥测对比见图6、7。

图6 蓄电池组放电电流仿真结果与遥测数据对比Fig.6 Comparison of discharge current simulation results and telemetry data

图7 蓄电池组电压仿真结果与遥测对比Fig.7 Comparison of battery voltage simulation results and telemetry
此次进入月影时蓄电池组处于搁置状态,对应容量约为50 Ah(该电池组满荷电态为75 Ah)。在进入月影后蓄电池组开始放电,最低放电电压仿真计算结果为33.88 V,遥测显示最低放电电压为33.87 V。由于采用平均负载进行仿真计算,因此仿真曲线较为平滑;而实际遥测由于功率负载会随着卫星工况的变化随之波动,因此电池组电压值也有明显的波动,但整体上仿真结果与遥测数据吻合。通过仿真确认,本次月影蓄电池组增加的放电深度在5%以内,荷电态在60%以上,满足放电深度不超过70%的指标要求,且月影过后蓄电池组自动完成充电,达到满荷电态,对航天器后续任务没有影响。在轨应用中,根据月影下能量平衡计算方法,一旦发现月影下蓄电池最大放电深度可能超过指标要求,可以率先将蓄电池组充电至满荷电状态。
经实际验证,月影期间太阳电池阵输出功率计算结果和能量平衡分析结果精度高,可以作为月影预测和能量平衡计算依据。
5 结束语
本文提出的月影状态下电源分系统的能量平衡计算方法,月影遮挡情况下的太阳电池阵输出功率、蓄电池组的放电深度计算精度均优于1%,通过仿真计算可以对月影前后电源分系统的工作状态进行准确的预测。中高轨航天器在轨运行期间,可以采用本文的方法结合航天器工况定期对月影影响进行预测分析,并可用于指导月影下航天器电源管理策略的制定。

