基于全局优选阈值列车走行部机会维护模型优化
贺德强,孙 一,苗 剑,农辉涛,罗 安
(1.广西大学 机械工程学院,广西 南宁 5300042.广西制造系统与先进制造技术重点实验室,广西 南宁 530004)
0 引言
列车车载设备的安全可靠运行是保证城市轨道交通车辆稳定有序运营的基础,城轨列车车辆设备的维修和维护工作尤其重要。目前,国内地铁列车检修大多沿用铁路机车车辆按运营里程和运营时间进行预防性计划维修的传统模式,以及列车发生故障以后进行的事后维修[1-2]。列车在运行途中发生故障会造成极大损失和影响,例如故障后的清客处理会极大影响列车正点率和运营服务水平。列车的预防性计划维修主要有日检、周检、双周检、月检等,该维护模式在一定程度上能够防止或延迟故障,但可能会出现过维修的现象。
针对上述两种维修模式的不足,有关学者提出将机会维护引入现有维修模式中,进而将预防性维修和故障维修相结合。机会维护指在系统停机对某些部件进行维护期间,同时判断其他相关部件是否满足机会维护的条件,若满足则一起进行维护[3]。引入机会维护可以有效解决预防性维护的过维修问题和故障维修带来的风险。
国内外学者在机会维护领域开展了一系列研究。Laggoune等[4]和王灵芝等[5]分别以部件的工作时间和可靠度作为机会阈值,判断是否对另一部件启动机会维护;侯文瑞等[6]基于风险水平,通过建立风险函数判断是否启动机会维护。针对多部件复杂系统,也有学者分别从经济、时间、故障、结构和功能等方面进行分类,并制定了相应的维修策略。Cheng等[7]和Shi等[8]以维修费用最低为目标,基于经济和随机相关性对系统机会维护策略进行研究;Geng等[9]基于多部件系统的结构和经济相关性,对部件采用多种方式进行维护;黄开敏等[10]提出一种考虑拆卸序列和随机故障的多部件机会维护策略。
以上研究从局部考虑引入机会维护的控制条件以及机会设备满足的预定条件,能在一定程度上降低维修成本,提高维修效率,但是没有考虑机会维护的方式,也缺少机会维护方式的决策模型,实际上机会维护方式的差异对检修费用的影响很大。考虑局部引入某个控制因素的机会维护往往存在欠维修或过维修的情况,也就是说机会维护虽然能减少维护准备费用,但是过度的机会维护也会造成维修资源浪费和对设备寿命的不完全应用。
因此,本文针对轨道交通列车走行部复杂零部件的运行特点和典型故障模式,基于故障之间的维修相关性,提出一种基于全局优选阈值的机会维护优化模型,该模型从机会维护的部位、时机、方式和判断标准4个方面全面考虑如何将预防性维修和故障维修相结合,在系统停机时,将与其相关并获得机会的部件提前采取机会维护,从全局优化角度使故障损失最低,形成一套针对列车走行部的故障预警防御方法。
1 列车走行部机会维护策略分析
本文引入机会维护,将计划性预防维修和事后维修有机结合起来,通过对轨道交通列车走行部零部件进行机会维护达到降低系统停机损失、最大化应用现有维修资源、降低系统零部件失效风险的目的。
机会型维修模型的关键是确定满足什么条件时才进行相应的机会型预防维修,包括[11]:①对系统中哪些部件进行机会维护(机会维护部位);②在什么时间进行机会维护(机会维护时机);③以什么样的方式对部件进行维护(机会维护方式);④采用怎样的判别标准进行维护(机会维护标准)。
1.1 机会维护部位
选择系统机会维护的部位一般需要遵循以下原则:
(1)故障与非故障部件之间具有相关性。机会维护往往以打乱预防性维修计划为代价,仅平摊系统的固定维修费用,这在很多情况下是不值得的。然而,当两部件在功能和结构上存在某种程度的相关性时,一个部件退化可能加速另外一个部件退化或者失效,从而诱发故障之间的耦合作用。因此,引入机会维护很有必要。
(2)故障与非故障部件的故障分布或维护周期一致或相近。
(3)根据实际情况,以部件的重要性顺序确定维修的优先级。有些部件虽然和停机维修部件的相关性较小,但是其对系统的重要性和行车安全性影响较大,也可以一起维护。
1.2 机会维护时机
预防性维修具有计划性,事后维修具有不可预知性,传统机会维护往往通过破坏预防性维修的计划性来实现,因此引入机会维护的时机是将事后维修和预防性维修相结合的关键;本文用机会维护役龄Tc(0 目前对部件采取的维修方式主要有完全维修(更换)、不完全维修和最小维修。完全维修是一种恢复至新的维修,部件的故障率经过完全维修后降为零,一般采取更换的方式;不完全维修是一种折中维修,维修后部件的故障率介于最小维修和完全维修之间;最小维修通常只恢复部件的功能,不改变部件维修之前的故障率。根据城轨列车维修的特性,为了更贴合实际,本文提出的基于全局优选机会维护策略采用的维修模式为:故障维修和机会修复为不完全维修;机会更换和预防性更换为完全维修。 机会维护役龄Tc仅从时间维度对部件是否进行机会维护进行约束,不能很好地解决部件维修中存在的过维修现象,因为系统中各个部件的失效分布情况各异,可能存在部件虽然达到机会维护役龄Tc,获得了维修机会,但是部件此时的可靠度仍然较高,基本没有执行机会维护的必要;同时机会维护还要考虑部件发生故障后对系统和行车安全的影响程度,有些部件虽然故障率较高,但是故障后对系统和行车安全影响不大,而有些部件虽然故障率较低,但是一旦故障则会严重影响系统和行车安全;另外,部件故障后的损失(计划外停机损失)也是是否对部件进行机会维护时需要考虑的因素。因此,本文基于全局优选机会维护策略,考虑在机会维护役龄Tc的基础上设置风险评估函数来约束部件进行机会维护的阈值Qi,其中Qi由故障发生的可能性(故障率)和故障引起的损失(计划外停机损失)决定。对Qi进行优选是本文的重点研究之一。 综上所述,在列车停运维修过程中,若走行部部件满足机会维护部位遵循的原则、役龄达到Tc及风险水平达到Qi,则可针对该部件采取更换或者修复的方式执行机会维护,达到对列车走行部预警防御的目的。 本文以观测周期T内的最小平均维修费用率为优化目标,对部件的机会维护役龄Tc和机会维护风险阈值Qi进行优化,从而获得列车走行部全局最优机会维护策略,如图1所示。 假定城轨列车走行部各部件的预防性维修役龄为Tp,机会维护役龄为Tc,机会维护风险阈值为Qi,则本文机会维护策略具体如下: (1)当走行部各部件的役龄处于(0,Tc)时,如果期间有部件出现故障,则对其采取修复如旧的最小维修。 (2)当走行部各部件的役龄处于(Tc,Tp)时,如果期间有部件出现故障,则对其采取事后维修;如果期间有其他部件因故障或预防性更换致使系统停机,则判断部件的风险水平,若超过Qi则执行机会维护,否则不执行机会维护,让其继续工作。机会条件下,对部件的机会维护分为机会修复(不完全维修)和机会更换(完全维修),进行机会修复还是机会更换,需要根据部件维护后减少的故障风险费用(利润)与维护费用(损失)的比率来决策。 (3)当走行部各部件的役龄达到Tp时,对部件实施预防性更换。 (1)设系统由N个不同的部件组成,各部件的故障率遵循Weibull分布,而且主要从故障及其耦合作用的客观存在性和经济相关性出发考虑部件之间的维修相关性。 (2)观测周期T内部件进行最小维修,故障维修和预防性更换的总次数为R。 (3)为了验算的需要,以列车定修周期(365 d)为一个观测周期。 (4)相同部件采用同种维修方式,不考虑相同部件之间的劣化程度因素。 城轨列车走行部的运行工况复杂,关键部件容易受疲劳载荷的严重影响,故障率会随时间的变化而变化。通过分析轨道交通车辆走行部各部件的历史故障数据表明,Weibull函数可较好地反映列车走行部各机械部件的故障分布。部件i关于时间t的失效概率密度函数为[12] (1) 式中:t为部件运行时间;β(β>1)为部件i的形状参数;η为部件i的尺寸参数。 部件i失效分布函数为[12] (2) 其可靠度函数为 (3) 可以近似地将部件的机会维护概率密度函数看作指数分布函数,则部件i的机会维护概率密度函数[13-14]为 (4) 根据上述列车走行部机会维护策略,在部件役龄处于(0,Tc)时,部件i进行最小维修的概率为 (5) 部件的役龄处于(Tc,Tp)时有两种情况:①部件自身出现故障时,对其进行故障维修;②由于其他部件出现故障或者对其他部件进行预防性更换致使系统停机时,对役龄处于(Tc,Tp)的部件进行机会维护判断,若Qi(t)达到风险水平阈值,则对该部件i进行机会修复或者机会更换。其中部件因自身故障进行故障维修的概率为 (6) 部件i因获得机会而进行机会修复或者机会更换的风险水平 Qi(t)=Z·ci(t)。 (7) 式中:Z为部件i的风险因子,Z∈[0,1],其体现了部件发生故障的概率;ci(t)为部件i出现故障导致的损失(计划外停机),ci(t)=C0+CiB,C0为系统单次停机维修的固定费用,CiB为部件i单次故障的维修费用。 假设在机会条件下,部件因提前被机会更换导致的剩余寿命损失为Pi[15],部件被更换时的可靠度为R(t),部件预防性更换时的可靠度为Rp,部件的等效寿命成本为Cr(这里取Cr=CiC,CiC为部件i单次预防性更换的费用),则部件的剩余寿命损失成本 (8) 部件修复和更换相应的费用为: (9) 其中:Si=CiB表示机会修复,Si=CiC+Pi表示机会更换。 部件被维护以后,因可靠度提高而减少的故障风险费用为Ai,则有 (10) 式中:Cc为部件故障后的费用,Cc=CiC+C0;R(t)为部件维修前的可靠度;R′(t)为部件维修后的可靠度, (11) 式中:θ为役龄回退因子,在[0,1]之间取值,其值与该部件的劣化情况、维修次数和维护方式有关,可根据经验得到;R′(t)=R(0)表示更换,R′(t)=R(θt)表示修复。 设更换参数为g,修复参数为x,则机会条件下维修方式M的决策为: (12) 其中M=Ig>Ix&Ig>1表示更换,M=Ix>Ig&Ix>1表示修复。 部件的役龄达到Tp时,根据工程实际对部件实施预防性更换的概率为 (13) 城市轨道交通列车的维修费用主要包括3类:①零部件直接维修的成本;②故障维修和预防维修产生的停机固定费用;③各个零部件未运行到允许的最低可靠度值而造成的剩余寿命未被充分利用的寿命损失成本。机会维护因为在系统停机期间进行,所以不包括固定费用。最小维修通常仅涉及一些轻微或者早期故障,而且维修时间相对较短,故不考虑固定费用。因此,系统在一段观测时间T内的维修总费用 Ci(T)=CiA·Ni[A]+(C0+CiB)·Ni[B]+ CiB·Ni[C]+(CiC+Pi)·Ni[D]+ (C0+CiC)·Ni[E]。 (14) 式中:CiA为部件i的最小维修费用;CiB为部件i的故障维修费用;CiC为部件i的预防性更换费用;Ni[A]为部件i实施最小维修的次数,Ni[A]=M·Ei[A];Ni[B]为部件i实施故障维修的次数,Ni[B]=M·Ei[B];Ni[C]为部件i实施机会修复的次数,Ni[C]=Ni[C]+1;Ni[D]为部件i实施机会更换的次数,Ni[D]=Ni[D]+1;Ni[E]为部件i实施预防性更换的次数,Ni[E]=M·Ei[E];C0为系统停机维修的固定费用。 由上述分析建立如下优化模型: (15) s.t. 0 (16) 式中W(Tc,Qi)为系统在观测周期T(单位:元/d)内的平均维修费用率。 在上述机会维护优化模型中,随着机会维护役龄Tc和风险阈值Qi的变化,走行部各部件的总维修费用及平均维修费用率也相应改变,本文基于动态仿真全局优选算法对机会维护策略进行优化,采用蒙特卡罗仿真法对系统中各选取部件的故障时间间隔进行抽样,按照仿真流程计算得到系统总维修费用和平均维修费用率。由蒙特卡罗原理知,当仿真次数足够大时,得到各次实验的平均值基本趋近真实值。 列车走行部机会维护过程仿真流程如图2所示。具体步骤如下: 步骤1输入已知条件,设定仿真时间Y、总仿真次数S和走行部各部件的预防性更换时间Tp;初始化各部件的维修次数和累计工作时间ti。 步骤2利用蒙特卡罗抽样技术产生走行部各部件的故障间隔时间Δti,并计算其预期发生故障的时间。选取其中的最小值Δtimin,当部件i最先发生故障时ti=Δtimin。 步骤3判断部件i的故障间隔时间Δti是否超过Tc,若未超过Tc,则进行最小维修,同时再次随机抽样产生部件i下一次的故障间隔时间Δti,令ti=ti+Δti;若超过Tc,则判断是否超过Tp,是则进行预防性更换,更新部件i的最近一次更换时间Tri,同时再次随机抽样产生部件i下一次的故障间隔时间Δti,令ti=Tri+Δti,否则进行故障维修,同时再次随机抽样产生部件i下一次的故障间隔时间Δti,令ti=θti+Δti。 步骤4针对其他未出现故障部件j(j=1,2,3,…,n),判断其余各部件j的故障间隔时间是否超过Tc,若超过Tc,则进一步判断是否超过风险阈值Qi,否则不维修,是则判断是否满足Ig>Ix&Ig>1,满足则启动机会更换,机会更换次数加1,更新部件j最近一次更换时间Trj,随机抽样产生部件j的故障间隔时间Δtj,更新其累计工作时间tj,令tj=Trj+Δtj;若满足Ix>Ig&Ix>1,则启动机会修复,将机会修复次数加1,同时再次随机抽样产生部件j的故障间隔时间Δtj,更新其累计工作时间tj,令tj=θtj+Δtj。 步骤5计算是否所有部件的累计工作时间ti均大于或等于仿真时间Y,若是,则仿真结束;若小于Y,则继续循环步骤2~步骤4。最后计算总维修费用和平均维修费用率。 本文选取城轨列车走行部轴承、抗侧滚扭杆、驱动轮对、减振装置4个部件为例,对机会维护模型进行计算验证;4个部件的编号分别为1,2,3,4。表1所示为列车走行部各选取部件的Weibull参数,二者由历史数据利用最大似然估计获得。表2所示为某B型列车单列车走行部所有同一类部件的单次平均维护费用,以及各部件的最优预防性维护周期。 表1 列车走行部各选取部件的Weibull参数 表2 列车走行部各选取部件的维修费用 首先,对传统机会维护阈值仅考虑时间因素、维修方式仅考虑更换的机会维护模型进行仿真;在各部件Tp已知的情况下,将各选取部件的机会维护役龄作为优化参数,以平均维修费用率最低为目标,得到平均维修费用率和机会维护阈值之间的关系曲线,并找出最低平均维修费用率及其所对应的机会维护阈值。设定仿真时间Y=365,总仿真次数S=2 000,步进长度为15 d,仿真结果如图3所示。 仿真结果显示,随着机会维护役龄Tc的增大,各部件的平均维修费用率先减小然后增大,该曲线符合实际维修经验。当机会维护阈值过小时,容易引起机会部件过维修,从而增大维护费用率;当机会维护阈值超过一定范围后,又会使部件故障率显著增大,导致部件突发故障增多,造成计划外停机增多,总维修费用增加,平均维修费用率增大[16]。当Tc=240时,平均维修费用率最小,为36.57元/d。 本文模型在对列车走行部各部件机会维护役龄阈值Tc进行优化的同时,重点考虑各部件的风险水平Qi,同时对机会条件下走行部各部件的利润—损失比率进行定量决策,针对不同部件比率使用不同维修方式,达到最经济维修的目的。 若部件的役龄处于(Tc,Tp),则根据式(7)对部件的风险水平进行定量判断,若超过风险水平阈值,则说明该部件拥有机会维护条件,计算其利润—损失比率,进而选择机会修复或机会更换,或者不维护。 在上述传统基于时间的机会维护阈值基础上,对部件风险水平阈值进行优化,以部件风险因子Z为参数,以最低平均维修费用率为目标,结合3.1节的算法进行仿真计算,设置步进长度为0.05,仿真时间Y=365、总仿真次数S=2 000。由于各部件的故障损失不同,为了简化运算,取各部件中故障损失的最低值作为风险阈值对应的故障损失,优化结果如图4所示。 从图4仿真结果可以看出,当风险因子为0.35时,各部件的平均维修费用率最低,为31.11元/d; 与传统仅考虑时间阈值的机会维护策略相比,考虑风险水平和利润—损失比率的机会维护策略减少的平均维修费用率为14.93%。以某地铁公司1号线30列B型列车(采用4动2拖的编组方式)为例,每列车包括走行部轴承12对,轮对12对,减震器8个,抗侧滚扭杆6根,则30列车一个观测周期T内可以节约维修费用约227.19万元。 以下为某次仿真过程中,部件1在t=280时发生故障,停机进行故障维修时各部件的机会维护方式决策结果,如表3所示。 表3 部件机会维护方式决策结果 由表3可知,在机会条件下,部件2和部件4的更换利润远小于更换损失,但其修复利润高于修复损失,因此对部件2和部件4采取机会修复的维修方式更加合理,若采用更换方式则会增加维修费用。针对部件3,其更换利润远低于更换损失,修复利润也低于修复损失,因此采用更换和修复都不合理,从仿真计算中发现主要是部件3的可靠度此时较高,该部件运行状态较稳定,进行机会维护的必要性不大,应让部件3继续运行,不对其进行维修。另外,从表中各部件的数据可见,部件采用机会修复比机会更换的利润—损失比率高出许多,这是由于在部件的可靠度较高时被提前更换的剩余寿命损失比较大,同时被更换部件本身的成本也比较高。因此,对机会条件下列车走行部各部件的维修方式进行决策具有重要的现实意义。 本文将故障风险水平和利润—损失比率引入城轨列车走行部各部件的维护中,充分考虑系统停机维修时各相关部件实施机会维护的可行性,建立了基于全局优选阈值的城轨列车走行部机会维护优化模型。该模型提出的多部件设备的机会维护策略有效克服了以往机会维护策略仅从局部考虑的不足,并将维修方式细化为机会修复和机会更换,同时给出机会维护方式的决策模型,更符合实际维修情况。本文从机会维护的部位、机会维护时机、机会维护方式和机会维护的判断标准4个方面全面考虑列车走行部各部件机会维护的条件,从全局优化角度实现故障损失最低,从而形成一套针对列车走行部的故障预警防御方法。考虑风险水平和利润—损失比率的机会维护策略可以减少平均维修费用率14.93%左右,有效控制了传统机会维护考虑因素单一引起的维护过剩问题,较好地解决了因各类维修而频繁停车,以及固定维修成本居高不下的问题。 下一步考虑将人工智能算法引入列车走行部机会维护优化模型,以加快仿真速度,同时有效减小模型复杂程度,为列车实现智能化维护提供技术支持。1.3 机会维护方式
1.4 机会维护判断标准
1.5 机会维护策略

1.6 建模假设
2 列车走行部机会维护模型
2.1 列车走行部部件的Weibull分布模型

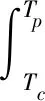

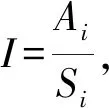
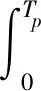
2.2 列车走行部部件优化模型
3 列车走行部机会维护模型的全局优选仿真
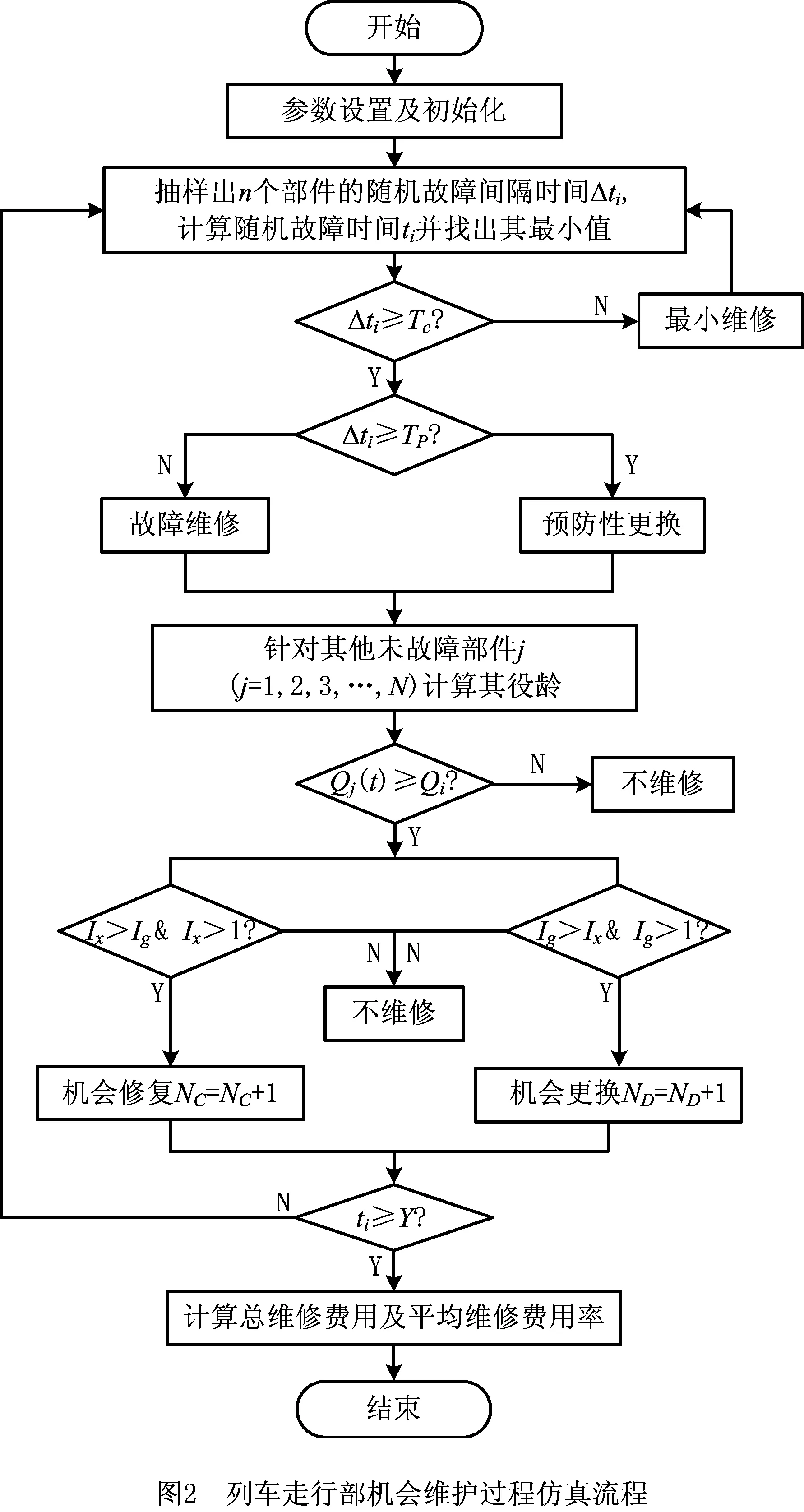
4 算例分析及比较
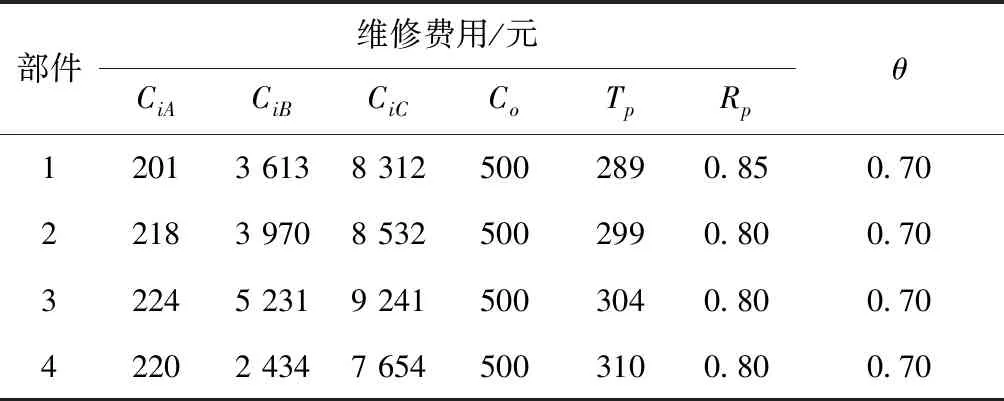
4.1 列车走行部部件的各个参数

4.2 仅考虑役龄的传统机会维护策略

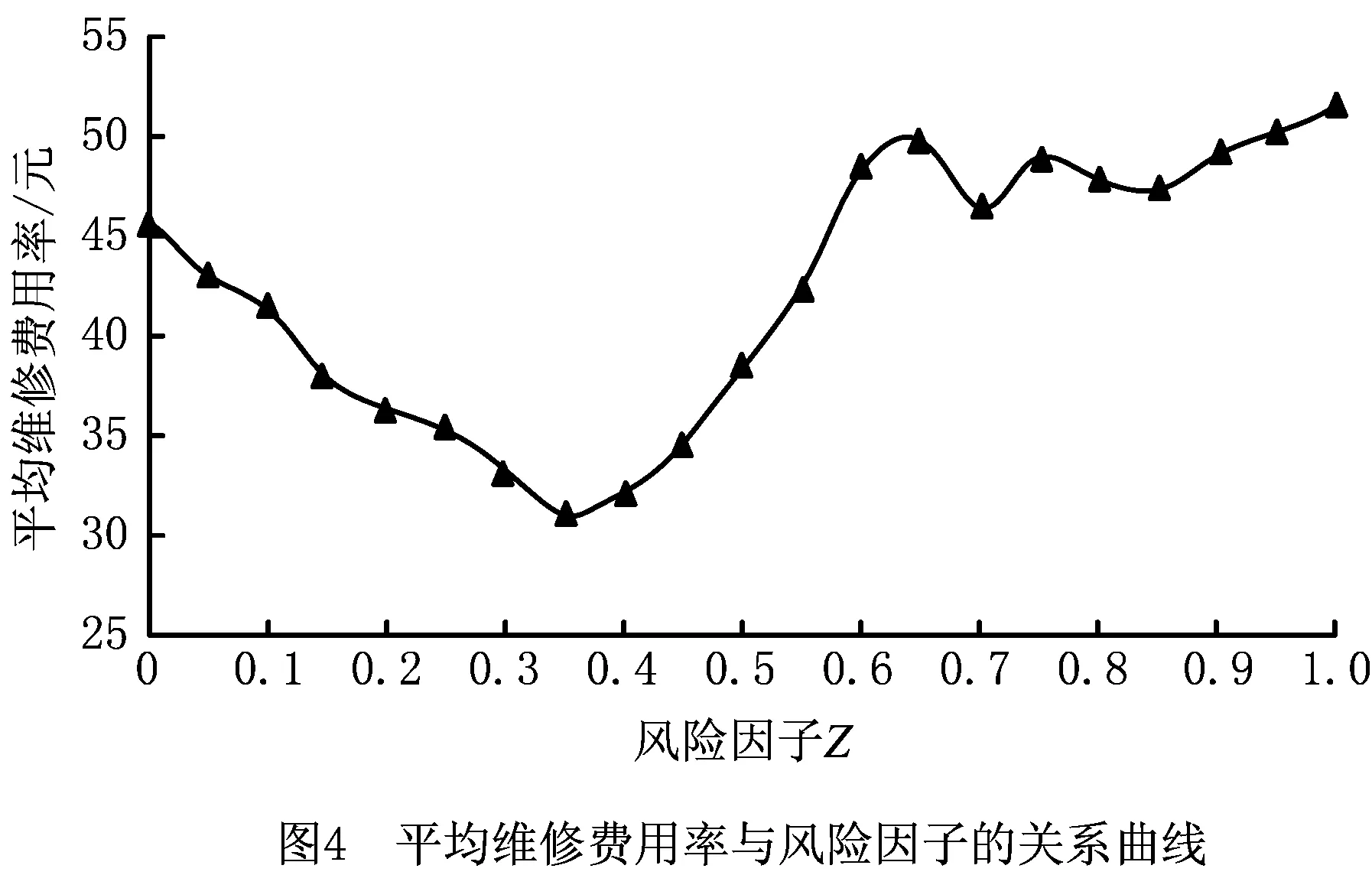
4.3 考虑故障风险水平和利润—损失比率的机会维护优化策略
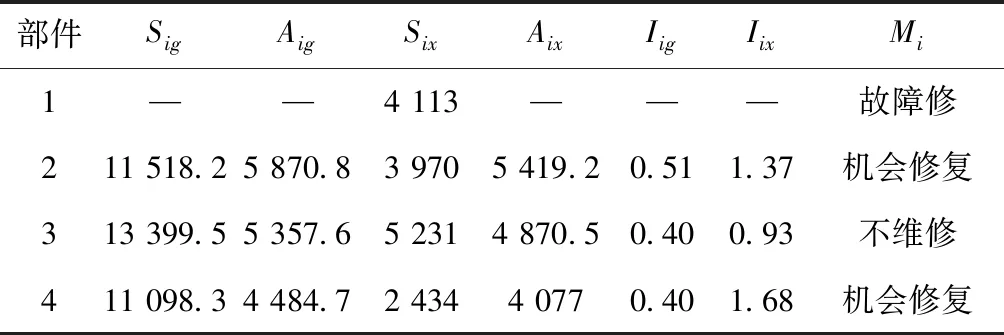
5 结束语

