磷虾群优化的改进粒子滤波算法

朱震曙，蒋长辉，薄煜明，吴盘龙

(南京理工大学 自动化学院，南京 210094)

在实际工程应用中，非线性系统无处不在.在这种应用背景下，基于卡尔曼滤波理论的滤波算法性能大大降低.

粒子滤波是一种基于蒙特卡罗方法和贝叶斯估计的统计滤波算法，利用大量带权值的随机样本来逼近状态.相对于传统的状态估计方法，粒子滤波没有状态函数、观测函数非线性和非高斯的限制，因此在非线性和非高斯的系统估计中有着广泛应用

标准的粒子滤波算法中，会出现权值退化现象[1-3]，表现为经过多次递推以后，只有少量粒子的权值较大，其余粒子的权值几乎为零.重采样可以解决权值退化问题，但也会带来样本贫化现象，即高权值粒子被过度复制，有效粒子数减少，导致粒子的整体信息容量降低.针对上述问题，国内外许多学者进行了大量的研究.文献[4]提出一种类电磁机制优化的粒子滤波，将采样粒子看成具有相互吸引和排斥的电荷粒子，通过电磁吸引力引导粒子运动，但是本质上仍然无法完全消除由重采样造成的样本贫化问题.文献[5]提出了基于引力场的粒子滤波算法，通过引力作用将粒子集中于高似然区域；文献[6]提出了一种自适应智能重采样粒子滤波算法，将粒子按权值大小分为两个子集；文献[7]采用了平方根嵌入式容积卡尔曼滤波产生的重要性密度函数，以此来提高滤波精度，这些算法在过程中都存在淘汰部分有效权值粒子的可能性，无法完全解决样本贫化问题.

近年来基于智能算法优化的粒子滤波成为一个重要的研究方向.很多学者将遗传算法、模拟退火算法、粒子群算法等引入到粒子滤波的重采样过程中，利用智能算法寻优引导粒子向高似然区域运动，这样可以提高粒子滤波的效率同时保持粒子的多样性.文献[8]提出一种利用遗传算法中变异、交叉操作的粒子滤波算法，修正权值较小的粒子，仿真表明该算法可以有效地保持粒子的多样性.文献[9]将粒子群算法引入到粒子滤波，文献[10]将蝙蝠算法引入到粒子滤波.文献[11]将一种改进的人工萤火虫算法和粒子滤波成功的结合，有效地提高了预测精度.群智能算法如果不针对粒子滤波的求解过程进行寻优策略的改进，就不能提高算法后期的寻优能力，在迭代过程容易陷入局部最优，如何快速寻找到全局最优解是亟待解决的问题.

磷虾算法[12](krill herd algorithm，KH)是由Gandomi和Alavi在2012年提出的一种群体智能优化算法.该算法来自于模拟地球南极海洋中的磷虾群体的行为，文献[12]通过仿真实验和常见的智能算法进行了对比.结果表明，磷虾算法具有更好的鲁棒性和全局搜索能力.但是直接将磷虾算法和粒子滤波结合容易出现局部最优现象，影响滤波精度.文献[13]提出了一种磷虾群免疫粒子滤波算法，该算法使用人工免疫算法中的变异操作优化了磷虾个体的分布情况，并将改进的算法用于粒子滤波中.但是根据文献[12]的表述，只使用遗传算法中的交叉操作效果更好.此外，该算法并未对磷虾个体位置变化的过程进行改进，无法在粒子滤波的不同时刻实时调整，影响了算法的性能.文献[14]在每次迭代中检测磷虾个体的运动状态来动态调整惯性权重，减少算法的无效迭代次数，但这种调整并不完全适用于粒子滤波.文献[15]将磷虾种群分为不同的子种群，进行二次寻优，提高了磷虾算法的局部收敛精度，但会降低收敛速度，不适合粒子滤波.

本文结合粒子滤波和磷虾算法的特点，提出了一种改进的磷虾算法优化粒子滤波 (improved krill herd algorithm optimized particle filter，IKH-PF)，动态地更新磷虾算法中诱导和觅食行为中的权值，并将改进的遗传算法交叉操作引入磷虾个体的更新过程，保证前期快速全局寻优，后期高精度局部寻优，提高了粒子滤波的精度，同时在寻优过程中并未舍弃低权值粒子，保存了全部粒子的信息，有效解决了样本贫化问题.

1 粒子滤波算法

粒子滤波基本思想是采用一组状态空间中的随机样本对条件后验概率密度函数进行近似，利用样本均值代替传统的积分运算，从而获得对非线性系统的状态估计如下：

xk=f(xk-1,vk-1)，

(1)

yk=h(xk,wk).

(2)

式中:xk为状态值；f(·)为状态函数；vk-1为系统噪声；yk为观测值；h(·)为观测函数；wk为量测噪声.

假设状态初始概率密度p(x0|y0)=p(x0)，则预测方程为

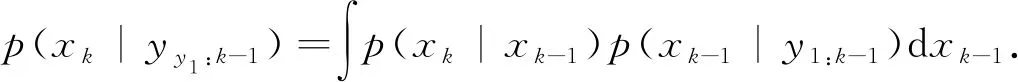
状态的更新方程为

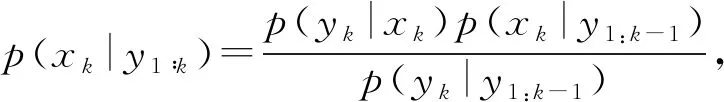
其中

重要性函数q(x0:k|y1:k)可以改写成如下形式:

则权值公式如下

(3)

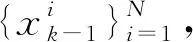
式中δ(·)为狄克拉函数，重要性权值更新如下

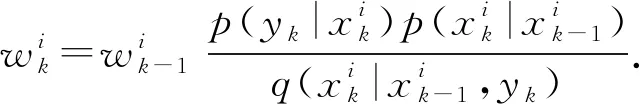
当粒子分布不满足贝叶斯滤波理论时，对粒子权值进行补偿和更新为

(4)

最后进行权值归一化，然后输出估计的状态如下：

(5)

(6)

2 磷虾算法

磷虾算法中，磷虾个体的位置变化主要取决于以下3个方面: 1)磷虾个体间的诱导运动；2)磷虾个体的觅食运动；3)磷虾个体的随机扩散运动.

具体公式如下

ΔXi=Ni+Fi+Di.

(7)

式中：ΔXi为第i个磷虾个体的位置变化;Ni为磷虾个体受诱导运动引起的位置变化；Fi为磷虾个体的觅食运动引起的位置变化；Di为个体的随机扩散运动引起的位置变化.

2.1 磷虾个体间的诱导运动

磷虾个体受到其他个体影响的行为可以表示为:

(8)

(9)

在磷虾群体中，相邻个体之间的影响定义如下：

(10)

(11)

(12)

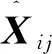
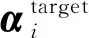
式中：rand为0和1之间的随机数；I为当前迭代次数；Imax为最大迭代次数.

2.2 磷虾个体的觅食运动

磷虾个体的觅食行为引起的位置变化可以表示为

(13)

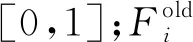
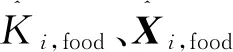
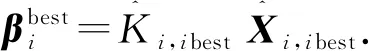
2.3 磷虾个体随机扩散运动

磷虾个体的物理随机扩散过程可以表示为

(14)

式中：Dmax为最大扩散速度；δ为随机的矢量方向，δ∈[-1,1].

3 磷虾算法优化的粒子滤波

在磷虾算法中，将粒子滤波中粒子的状态值作为磷虾群的个体位置，则个体适应度值最好的磷虾相当于权值最高的粒子.由此，粒子滤波的求解过程就可以转化为磷虾群的寻优过程.针对粒子滤波的特点，需要对磷虾算法进行改进，来提高算法的寻优效率和保持粒子多样性.

3.1 诱导权值和觅食权值的改进

根据文献[16]的证明，磷虾个体适应度值可以表示为：

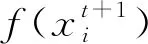
磷虾算法参数调整研究还很少，IKH-PF在求解过程中用到的适应度函数都为单峰值函数，本文主要参考文献[16]对于磷虾算法参数在单峰值函数下的测试结果，对权值wn和wf进行动态调整，设计了新的更新策略.当权值wn和wf取0.9时，在前几次迭代中，磷虾群就能迅速寻优；当权值wn和wf取0.1和0.3之间的值时，磷虾群的寻优结果稳定且准确；当权值采用线性递减时，算法寻优结果平稳，鲁棒性强.综上所述，本文提出线性函数和倒数函数相结合的非线性递减策略，更新公式如下

(15)

式中：I、Imax分别为当前迭代次数和最大迭代次数；w1、w2为需要设置的参数.

当w1=0.2,w2=0.6,Imax=20时，得到的权值变化曲线如图1所示.

从曲线图可以看出，在前5次迭代中，权值迅速减少，后10次迭代权值近似线性递减，符合之前的理论分析.

图1 权值变化曲线

3.2 磷虾群多样性改进

为了保持磷虾种群的多样性，需要将遗传算法引入磷虾种群寻优中.适用于磷虾算法的遗传算法包括交叉和变异操作，只执行交叉操作的效果更好[12].经典的遗传算法采用固定的交叉概率，但这种策略并不符合粒子滤波过程对于磷虾算法寻优的要求.因此，本文提出一种改进的交叉概率变化公式，提高磷虾群的多样性，最终提高算法的性能并保持粒子的多样性.

交叉概率可以控制磷虾种群新个体产生的速度.针对粒子滤波的应用环境，寻优初期，交叉概率取较大值，提高磷虾种群新个体产生的速度来保持种群的多样性，从而提高算法前期的全局寻优速度；寻优后期，交叉概率取较小值，保存较优的磷虾个体，从而提高局部收敛能力.由此设计的交叉概率更新公式如下

PC=PC0·e-2I/Imax,

(16)

式中PC0为需要设置的参数.

当PC0=0.9，Imax=20时，得到的交叉概率变化曲线如图2所示.

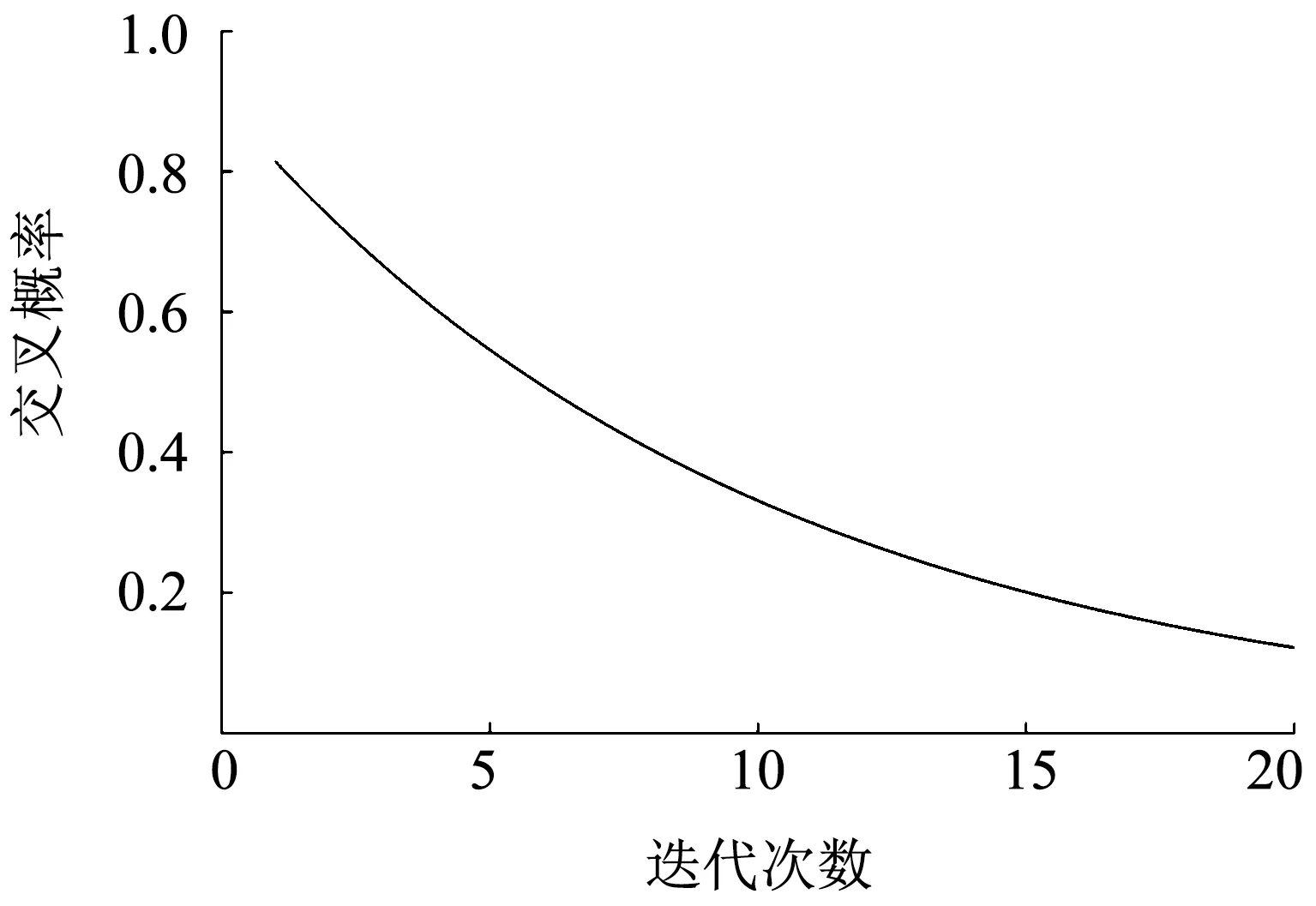
图2 交叉概率变化曲线

从图2可以看出，随着迭代次数的增加，交叉概率逐渐减小，符合粒子滤波求解过程的要求，同时在后期仍然能保持粒子的多样性.

3.3 算法收敛性分析

在磷虾算法中，令d(x(t),x*(t))表示当前磷虾个体位置与全局最优位置之间的距离，简化表示为d(x(t))，当x(t)≠x*(t)时，d(x(t))>0.对于一次迭代的解集X(t)={x(1),x(2),…,x(N)}，令d(x(t))=min{d(x(t)),x∈X}，可以得到每次迭代种群间的移动Δd(x(t))=d(x(t+1))-d(x(t)).以此定义迭代终止时间为

τ=min{t:d(x(t))=0}，

式中τ为第1个磷虾个体到达全局最优位置的时刻.如果E[τ]存在有限值，则算法最终就是全局收敛的.

文献[15]已经证明了标准磷虾算法满足以下两个约束条件，并进一步证明在约束条件下算法是收敛的.

条件1存在一个规模为m的多项式λ0(m)>0，使得d(x(t))≤λ0(m).

该条件说明每代磷虾个体和全局最优位置之间的距离在一个多项式范围内.

条件2存在一个规模为m的多项式λ1(m)>0，使得：

该条件说明当磷虾个体不断接近全局最优位置时，种群的移动限定在一个多项式倒数的范围内.

满足以上两个条件时，可以给出磷虾算法的时间估计E[τ]为

E[τ|d(x(0))>0]≤λ(m)，

因此，算法是收敛的.

本文对于诱导和觅食运动中权值更新策略的改进，只是改变了不同时期磷虾个体的运动速度，权值本身的取值仍在基本磷虾算法的范围之内，因此这项改进使算法仍然满足条件1和2；磷虾群多样性改进中对于交叉概率更新的改进，同样只是在不同时期采用不同的交叉概率，以增强群体的多样性，对磷虾群整体的移动没有改变，因此没有改变条件1和条件2.综上所述，本文提出的IKH-PF在迭代过程中，磷虾群是朝着全局最优位置移动的，存在可估的终止时间，算法是收敛的.

3.4 算法实现步骤

改进的磷虾算法优化的粒子滤波具体实现如下：

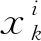
步骤3更新粒子状态. 根据提出的式(15)计算诱导和觅食权值，然后按照式(8)、(13)、(14)计算磷虾个体的诱导、觅食和扩散运动，最后根据式(7)计算每次迭代中磷虾个体的位置变化.

步骤4按照式(16)计算交叉概率，对磷虾群个体进行交叉操作.

步骤5设置一个迭代次数，判断是否达到设置的迭代次数，否则执行步骤3.

步骤6重新计算每个粒子的权值，按照式(4)对粒子权值进行补偿和更新，按照式(5)对权值归一化处理，最后按照式(6)输出每个粒子当前时刻估计的状态值.

步骤7重复执行步骤2～6，直到k=NK，完成NK个时刻的粒子状态估计.

由于磷虾算法的收敛性强，IKH-PF的终止条件为达到设置的迭代次数，使得磷虾个体向最优区域移动，但避免最终收敛.这样不仅可以保证粒子全部分布于高似然区域附近，保持粒子的多样性，同时也可以降低算法的复杂度.

4 仿真实验和分析

为了分析和验证算法的性能，选取一种单静态非增长模型，仿真环境为Matlab 2016a.

仿真实验中采用的单静态非增长模型的状态方程和观测方程如下：

8cos[1.2(t-1)]+ω(t),

式中:ω(t)、v(t)均为零均值高斯白噪声，ω(t)的方差Q在不同仿真中分别设为1和5，v(t)的方差R=1.在磷虾算法中，仅对粒子状态值进行估计，所有参数均没有单位.最大诱导速度Nmax设为0.2，个体觅食速度Vf设为0.1，最大随机扩散速度Dmax设为0.05，最大迭代次数Imax=20，w1、w2分别设置为0.2和0.6.

为了进一步验证算法的性能，在仿真实验中同时和标准的粒子滤波、粒子群优化粒子滤波(PSO-PF)和蝙蝠算法优化粒子滤波(BA-PF)进行了对比.

4.1 算法的精度测试

算法的精度测试主要在以下3个条件下进行：

1)粒子数N=20，Q=1，仿真结果和估计误差绝对值如图3、4所示.

图3 滤波状态估计(N=20，Q=1)

图4 估计误差绝对值(N=20，Q=1)

2)粒子数N=50，Q=1，估计误差绝对值如图5所示.

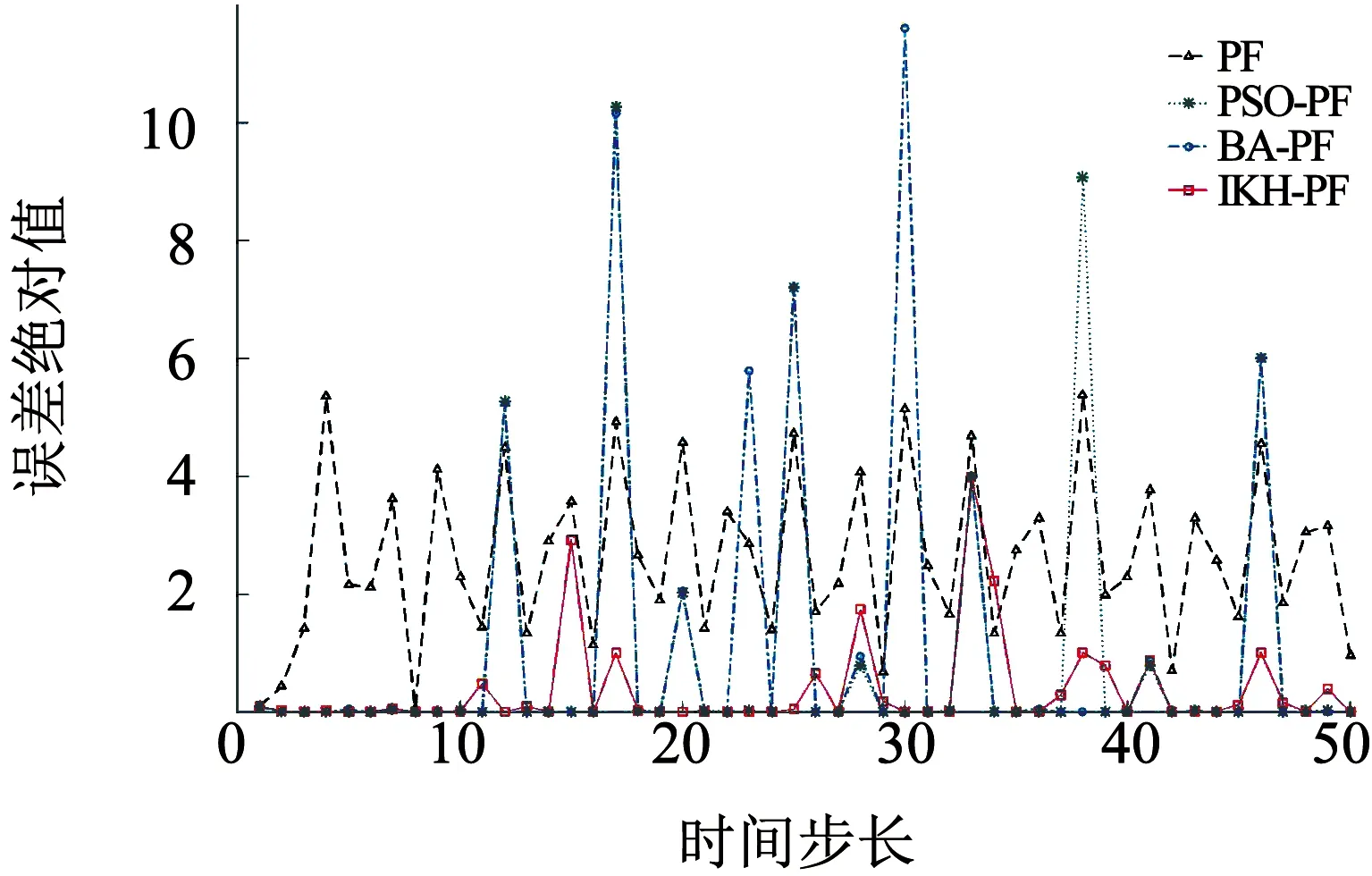
图5 估计误差绝对值(N=50，Q=1)

3)粒子数N=100，Q=1，估计误差绝对值如图6所示.

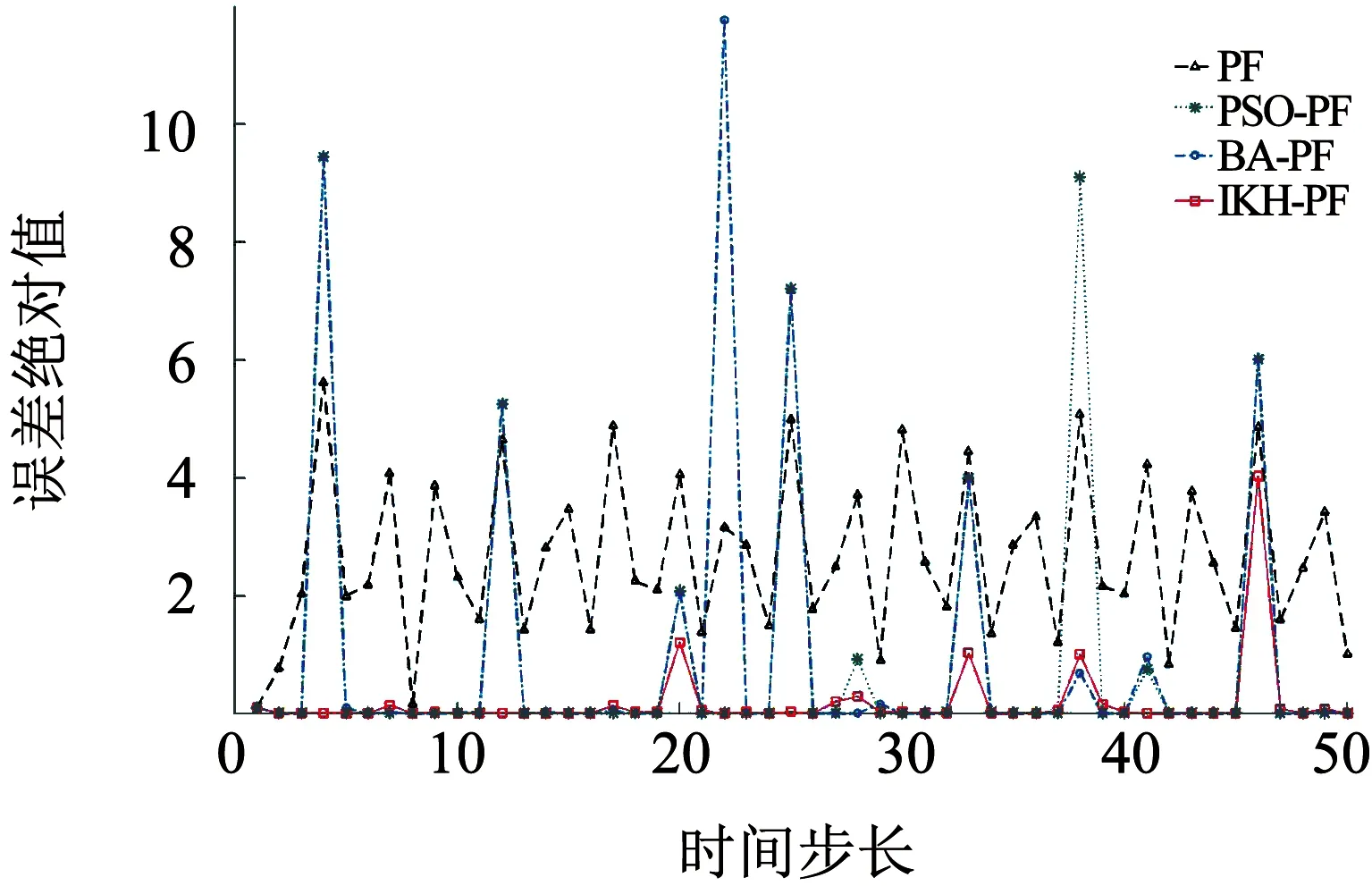
图6 估计误差绝对值(N=100，Q=1)

不同条件下整体误差采用均方根误差为

表1 整体误差对比

从图3～6可以看出，在相同的粒子数条件下，相对于标准PF、PSO-PF和BA-PF，IKH-PF具有更好的状态估计精度，这是因为磷虾算法迭代寻优之后的粒子分布更加合理，从而提高了粒子滤波的精度.从图4～6的误差绝对值可以看出，相对于PSO-PF和BA-PF，IKH-PF由于改进了诱导和觅食权值更新策略，在一些容易陷入局部最优的位置，具有更好的收敛精度.从表1的数据可以看出，当实验次数为50次时，本文提出的IKH-PF相对于其他3种算法，整体误差是最小的；当噪声方差变大时，IKH-PF误差也没有明显变化，体现了该算法的稳定性.由于动态调整了权值和交叉概率，IKH-PF在粒子数为20时的精度已经高于其他算法在粒子数更多情况下的精度，体现了算法的运行效率.

4.2 粒子多样性测试

为测试粒子的多样性，将仿真的最大运行时间步长设置为50，粒子数设置为100.这里选取了运行步数k=8，27，47时的粒子分布情况.粒子分布情况如图7～9所示.

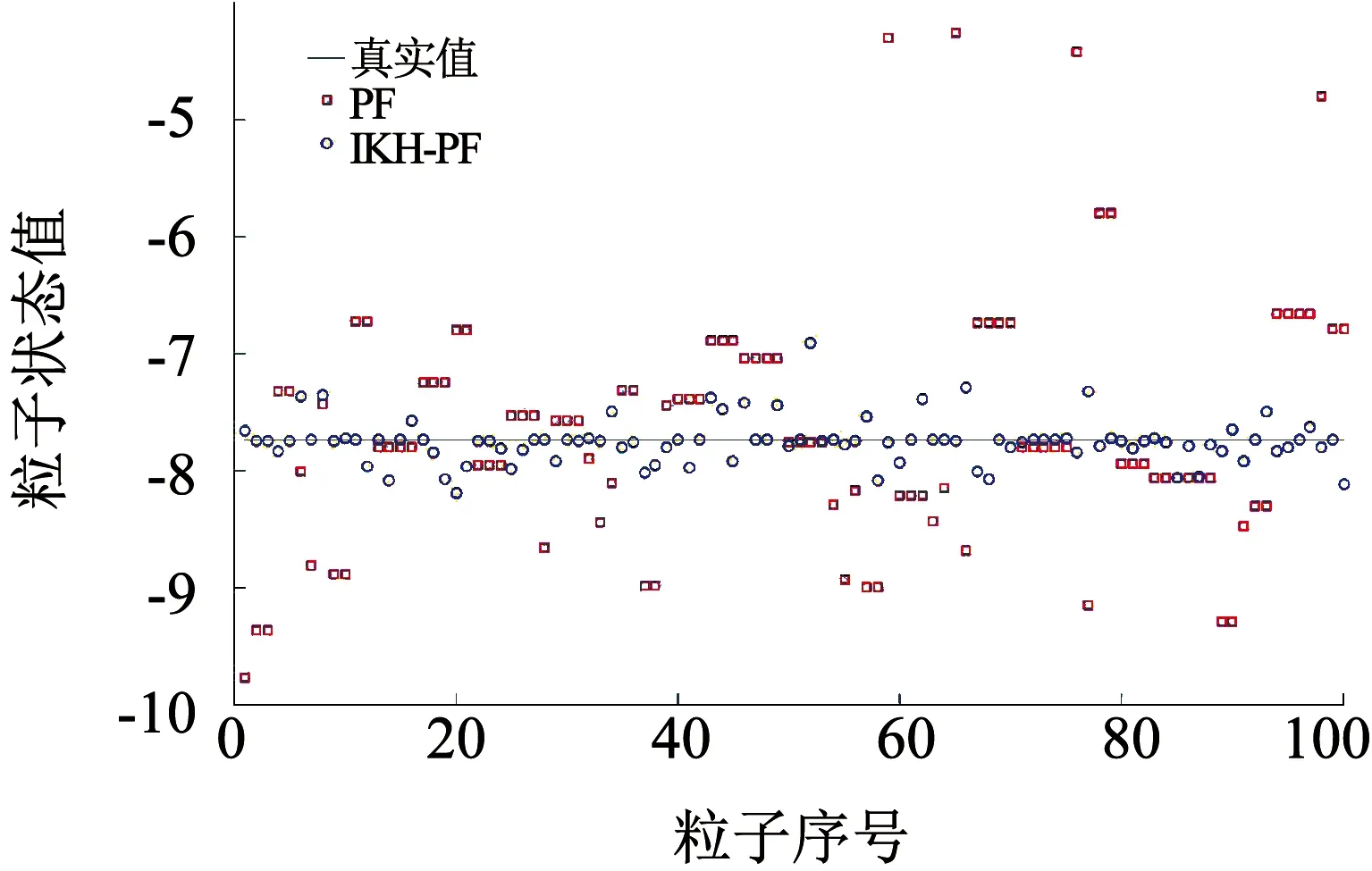
图7 k=8时粒子分布

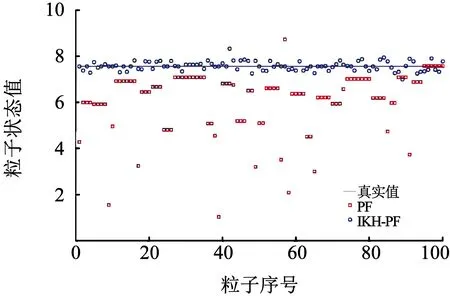
图8 k=27时粒子分布

图9 k=47时粒子分布

从图7～9可以看出，在标准的粒子滤波算法中，由于重采样时只采用权值较大的粒子进行状态估计，导致粒子分布于少数状态值上，出现了样本贫化现象，不利于整体状态估计.对于进行了交叉操作的磷虾算法，其优化的粒子大部分处于高似然区附近，也有少部分粒子分布于其他区域，整体保持了粒子的多样性，有效地避免了样本贫化现象.

5 结 论

1)为解决粒子滤波中的样本贫化问题，本文结合粒子滤波和磷虾算法的特点，采用改进的磷虾算法优化粒子滤波.

2)针对粒子滤波，在磷虾算法中改进了诱导和觅食运动的权值更新策略；同时为了保持粒子的多样性，对磷虾个体进行交叉操作，设计了新的交叉概率更新公式，以磷虾群的寻优引导粒子向高似然区域移动.

3)仿真结果表明，提出的IKH-PF相对于标准的粒子滤波、PSO-PF和BA-PF具有更高的状态估计精度，同时在运行后期能够保持较好的粒子多样性，避免了样本贫化现象.