不同张拉顺序下的斜拉桥施工索力分析

杨 雄

(兰州交通大学土木工程学院，甘肃兰州 730070)

0 引言

斜拉桥属于高阶超静定结构，斜拉索起着关键作用，通过对施工索力的精确计算，桥梁成桥索力可以精确收敛于设计的成桥索力。

斜拉桥索力张拉一般采用2次张拉，为了保证成桥后索力能够达到设计索力值，需合理确定斜拉索施工索力［1］。现有的有限元软件无法直接求出合理施工索力，在实际工程应用中，应用正装迭代法确定施工索力时，一般靠工程人员结合有限元软件进行正装分析，该过程需要不断地输入、提取大量数据［2］。本文基于的差值法确定施工索力的基本原理是给定任意1组施工索力后进行正装计算得到新的成桥索力，求出该成桥索力与设计成桥索力之间的差值，将其与该次正装计算的初拉力相加后作为下一轮迭代计算所需要初拉力。这种方法不需要提取影响矩阵且数据处理简单，宜于实际工程应用［3，4］。

1 工程概况

西北某斜拉桥为1座独塔双索面非对称混合梁斜拉桥，采取塔墩梁固结体系，跨径布置为158 m+45 m+40 m，其中辅跨45 m+40 m，为预应力混凝土结构，主跨长158 m，为钢箱梁，钢混结合部伸入主跨，距桥塔中心线15 m，梁高均为3 m。采用双索面，扇形布置，索体系平行钢丝冷铸锚式索。每侧索面共有24根斜拉索，全桥共48根斜拉索，斜拉索顺桥向间距为10 m(钢梁侧)和5 m(混凝土梁侧)。主跨水平索距由主塔中心左起为28 m+11×10 m+20 m，主塔一侧无索区为28 m，边墩无索区长度为20 m。边跨水平索距由主塔中心右起20 m+11×5 m+10 m，主塔一侧无索区为20 m，边墩无索区长度为10 m。该斜拉桥总体布置立面图和拉索编号如图1所示。

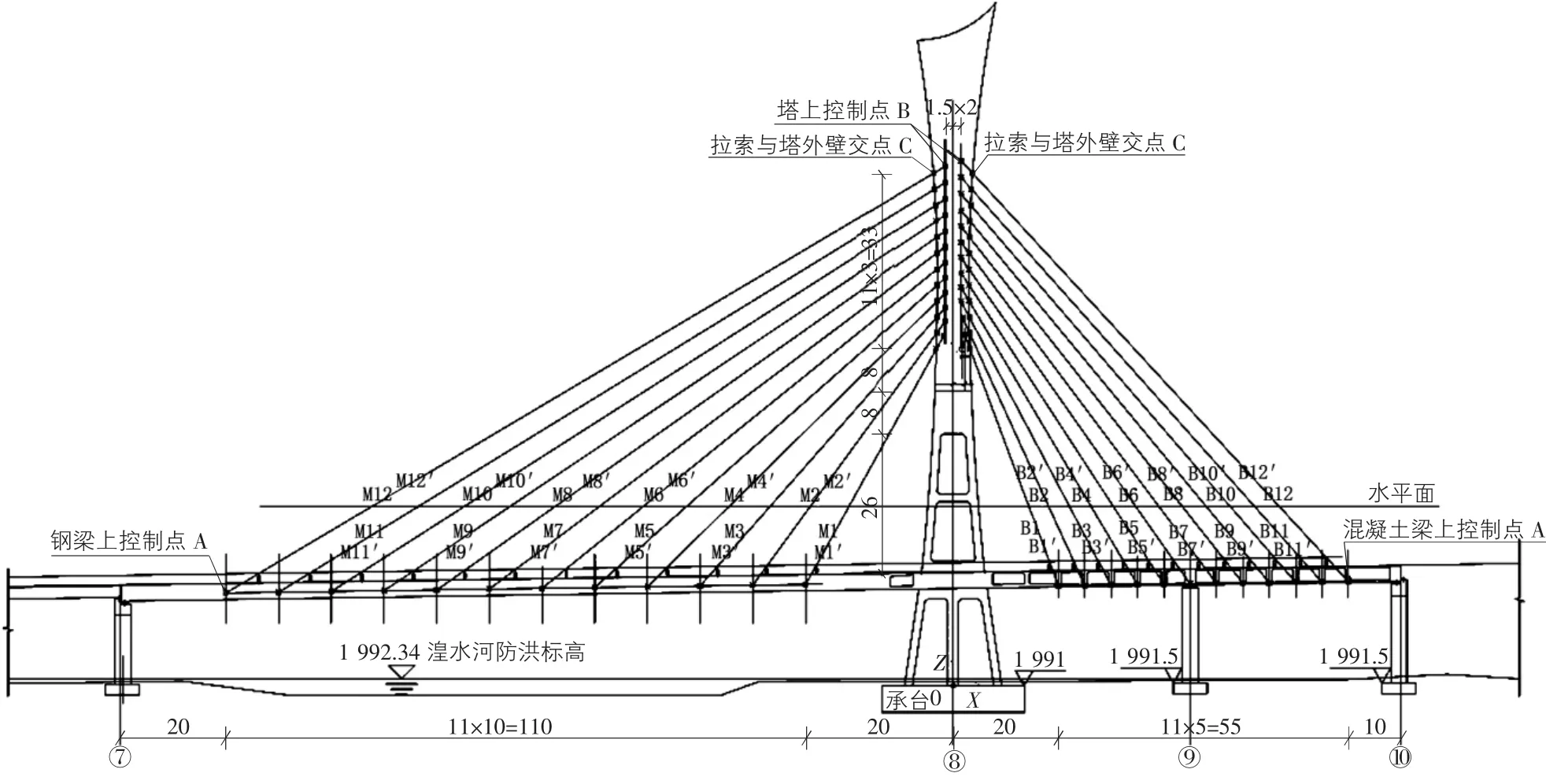
图1 斜拉桥总体布置立面图

2 张拉顺序

该斜拉桥辅跨混凝土梁采用满堂支架施工，主梁钢箱梁采用钢栈桥施工，主梁和主塔全部施工完成后进行斜拉索张拉。拉索采用2次张拉，原张拉方案为:①第一次张拉从塔端处开始两侧同时对称张拉4根拉索，依次顺序张拉，即 Mi，Mi'，Bi，Bi'(i=1，2，3，4，…，12)同时张拉，第二次施工顺序同第1次张拉。但由于现场采用对称张拉时，前三组索的张拉用千斤顶的放置空间不足，经施工单位、设计单位、监理单位、监控单位互相沟通，现场张拉方案改为:②前三组索第1次张拉从塔端处开始两侧同时对角张拉2根拉索，即先完成 Mi，Bi'(i=1，2，3)号索的张拉后，再进行 Mi'，Bi(i=1，2，3)号索的张拉，从第四组索开始，第1次张拉从塔端处开始两侧同时对称张拉4根拉索，依次顺序张拉，即Mi，Mi'，Bi，Bi'(i=4，5，6，…，12)同时张拉，第二次施工顺序同第1次张拉。

该斜拉桥有限元模型采用软件Midas Civil(2015)建立，结构采用单梁模式;桥墩、桥塔、主梁采用空间梁单元，拉索采用桁架单元;桥墩底弹性固结，墩、梁、塔刚性连接，拉索与梁、塔刚性连接。该斜拉桥有限元模型如图2所示。

图2 全桥有限元模型

3 不同张拉顺序下的施工索力

在两种不同张拉顺序下，采用差值迭代法，经过多次迭代直到施工索力满足精度要求，得到该斜拉桥的一张、二张施工索力，主要结果汇总见表1，表2。

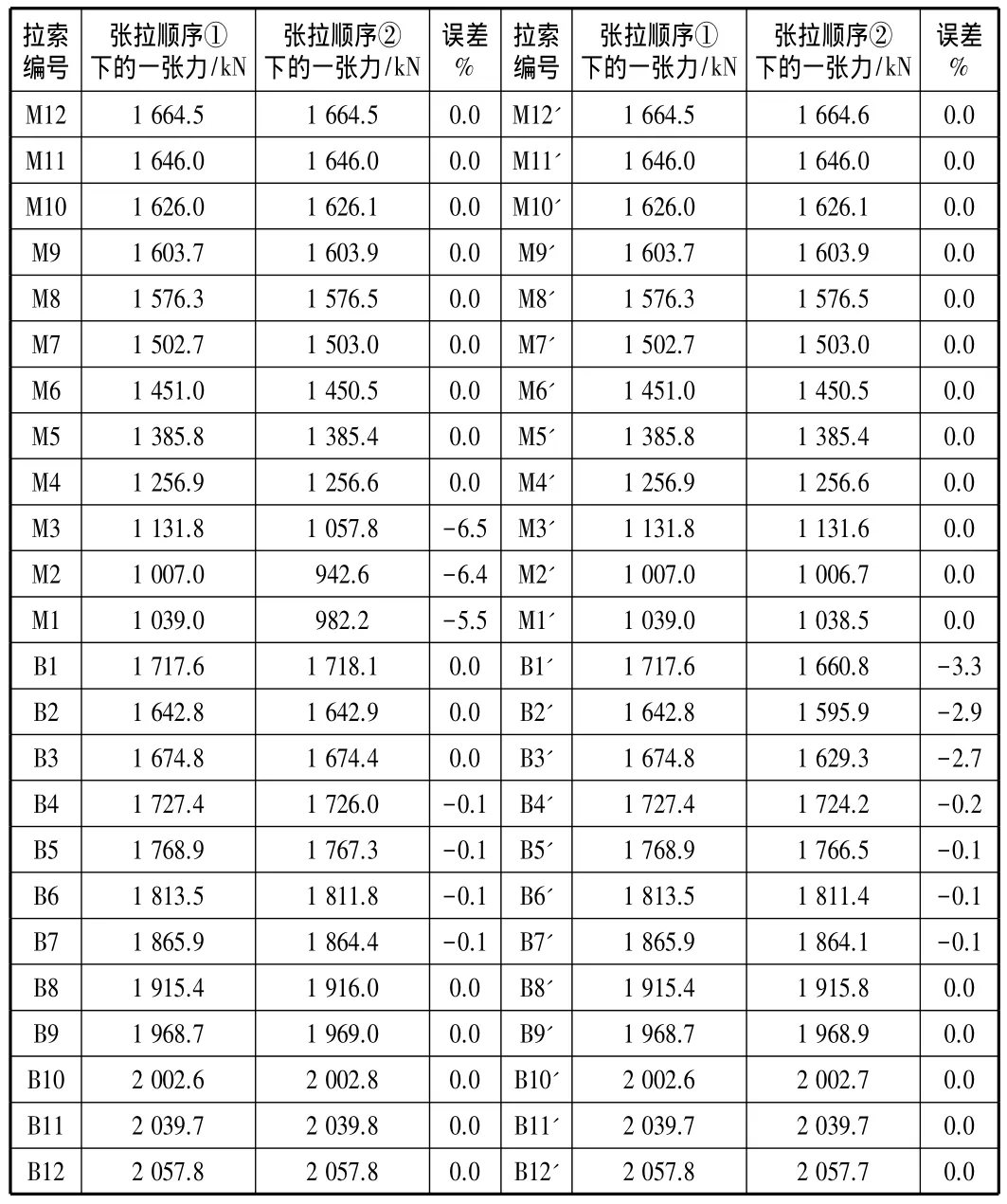
表1 两种不同张拉顺序下的一张力结果汇总

由表1可知:两种不同张拉顺序下得到的第一次施工张拉索力大致相同，只有前三对索的张拉索力相差比较大，成对角分布，但误差都在7%以内。说明张拉顺序的改变对第一次张拉索力的影响不大。

表2 两种不同张拉顺序下的二张力结果汇总

由表2可知:在钢箱梁侧两种不同张拉顺序下的二张力从12号索到1号索误差逐渐变大，符合规律;混凝土梁侧两种不同张拉顺序下的二张力变化不大。总的来说张拉顺序的改变对第二次张拉索力的影响较大。

4 结语

1)斜拉索张拉顺序改变根数比较少时，对第一次张拉索力影响不大，施工时可考虑第一次张拉索力不变，为技术人员节省时间。

2)拉索张拉顺序改变时，对第二次张拉索力影响较大，技术人员必须重新进行准确的计算得到第二次张拉索力，否则成桥索力难以满足设计与规范要求，必需耗费人力物力进行一次全桥调索，得不偿失。