典型地质条件深部岩巷锚杆长度的选择

丁昌伟 吴德义

(安徽建筑大学土木工程学院，安徽合肥 230601)

0 引言

巷道开挖时大量进行支护工作，支护工作不仅占用时间长，而且也与煤矿安全生产工作息息相关，运用锚杆(锚索)进行支护，不仅费用成本低，而且工作效率高，在支护强度方面也有强有力的保障，现如今已成为主流的支护方式，在工程实例中，工程技术人员普遍运用松动圈厚度理论来进一步确定锚杆(锚索)及其组合方式。本工程以淮北矿区许疃煤矿3238底抽巷为实例，采用Flac 3d软件，在地质条件主要为砂岩的情况下，试验将锚杆长度由原先的2 400 mm转变为2 000 mm，观察围岩支护过程中产生的应力变形情况，选择正确的支护参数［1］。

1 工程概况

巷道位于许疃煤矿3238底抽巷11 m～32 m处，地下部分的岩石种类存在有粉砂岩，细砂岩和泥岩，在巷道开挖支护过程中，排出的土质主要由粉砂岩，细砂岩和泥岩组成，泥岩表观颜色为深灰色，岩石规格呈块状，断面缺口参差不齐，在含有少量有机质的根部位置，岩石质地紧密，下部位置含有砂质成分，细砂岩外观颜色为青灰色，岩石内部架构组分最高的为硬质石英［2］，岩石层理相互交叉，硅质部分相互胶结，粉砂岩，表观颜色为灰色，岩石规格呈块状分布，断面缺口呈现为平坦状，少部分位置含有细砂质成分。巷道地面标高 ［25.42，25.82］，工作面标高［657.60，747.00］。

2 巷道围岩力学性质测定

在现有的实验室条件下，制作芯样并进行选取，由实验可得岩石弹性模量和泊松比等力学参数［3］。

2.1 岩石力学试验程序

1)依据试验条件，将试验所需选用的岩石进行破碎切割，制作为直径 50 mm，高径比为 2 ∶1，1 ∶1 的试块。

2)将原先准备好的试块，按顺序整齐的布置在承压板的中心位置，调整带有压力板球形底座的高低位置，让试件受均布荷载作用。

3)匀速的对试块进行加载试验，速度保持在0.5 MPa/s～1.0 MPa/s，试块发生明显变形时，得出试件破坏的荷载值及增加荷载时出现的表观状态。

4)根据每组试块的个数进行单轴抗压强度试验，每组要求3组，单轴抗压强度能够一定程度上反映岩石抵抗外荷载的能力，从而得到试验所需要的岩石力学参数。

2.2 现场实验结果

由实验室结果可得，砂岩的泊松比λ=0.25，弹性模量E=7.2 GPa，粘结力 c=4.0 MPa，内摩擦角为 30°。

3 工程分析

1)模型尺寸及边界条件。

工程中关于连续介质模型的边界条件有三种［4，5］，第一种被称为应力边界条件，巷道表面部分受到均布荷载和集中荷载的双向作用，第二种被称为位移边界条件，注意边界位置上是否存在位移变化，在边界位置上如果未观察到位移变化，则约束条件被满足，第三种被称为混合边界条件，此时在一个方向出现已知力，位移变化存在于其他边界位置上。在软件模拟分析的过程中，边界约束条件是我们必须要考虑的，我们在使用软件模拟的过程中，要充分考虑到边界条件与实际情况的差异，尽量模拟出与实际情况相类似的条件，以此来保证实验结论的准确，尽可能在模拟条件下达到误差的降低。与此同时，我们要有足够大范围的计算模型，保证分析的关键部位位于模型的正中部分。

2)支护方式。

淮北矿区许疃煤矿巷道周围岩性为砂岩，为了能够更好的起到约束作用，选用锚网喷射混凝土再加上锚索双向受力进行补强，在双重作用下增加围岩的稳定性，再加入直径20 mm长度为2 400 mm的高强度锚杆，两根锚杆之间的距离为800 mm×800 mm。将冷拔带肋钢筋进行组合焊接，制作成为6 mm钢筋网片，长宽为2 100 mm×900 mm，孔眼大小为150 mm×150 mm。使用长度6 200 mm，使用专业机具将半径为8.9 mm的钢绞线绞制成锚索，间排距为1 600 mm×1 600 mm，在巷道中顶及两边对称均匀布置3根，如图1所示。

4 数值模拟

4.1 锚杆长度选择

如图2所示，由数值模拟可得，巷道围岩条件为砂岩时，锚杆长度l=2 400 mm偏大，因此选用长度l=2 000 mm的锚杆。

4.2 松动圈厚度理论

1)围岩位移场数值模拟结果。

如图3所示在O1O2方向，初始位置位移量最大，下降速度也最快，后期当巷道表面距离继续增加时，位移量开始缓慢下降，两者关系适用于回归方程:

其中，k1，k2均为回归方程系数。

采用最小二乘法回归，可得:围岩岩性为砂岩时，k1=27.0，k2=1.01。

由式(1)可得在距离巷道表面r位置，围岩体积碎胀系数k为:

2)深部巷道围岩破碎松动理论分析。

由式(2)可知，巷道表面距离r的变化与围岩在O1O2方向不同位置围岩体积碎胀系数k存在相互作用，其影响程度如图4所示。

如图4所示，巷道围岩表面部分体积碎胀系数k值较大，表征围岩破碎显著，碎胀程度高。随着巷道表面距离r的增加，围岩体积碎胀系数k值下降的也越明显，当k值缩减到临界值kmin时，围岩的状态发生改变，由原先存在的松散剥落的表现形式逐渐转化为内部存在裂隙的塑性表现形式，参考围岩体积碎胀系数找到松散破碎区域的位置，由试验结果可得:不同情况下临界破碎时的体积膨胀系数可取为kmin=10.0 mm/m，由此确定松动圈厚度Lp。

图2 围岩支护变形情况

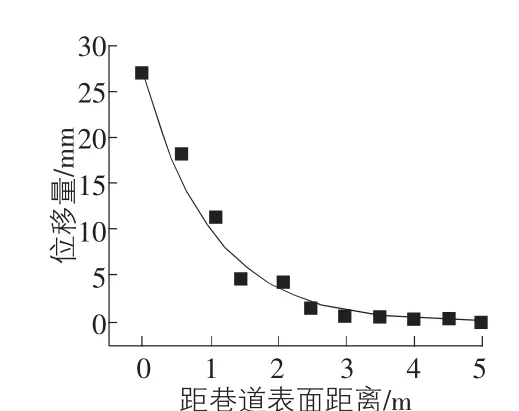
图3 巷道表面距离—位移量关系图

图4 体积碎胀系数

根据图2数值模拟结果，采用式(1)进行回归分析得出的围岩岩性为砂岩时回归方程系数，巷道围岩附近土质条件为砂岩时松动圈厚度Lp=1 100 mm。

3)锚杆长度的确定。

根据松动圈实测数据可得，巷道围岩附近土质呈砂岩时，可以定为中等松动圈Ⅱ类稳定围岩，依据松动圈理论来确定锚杆长度的数值，锚杆长度可由式(4)算得:

其中，Δl1为锚杆外露长度，取 Δl1=100.0 mm;Lp为松动圈厚度，取Lp=1 000.0 mm;Δl2为锚杆进入松动圈外长度，取 Δl2=300.0 mm。

未来开采过程中还会存在其他影响因素，松动圈范围Lp增加，锚杆长度最大为l=2 000.0 mm。因此选用锚杆长度l=2 400.0 mm不太合理。

5 实验结论

当围岩周边地质条件为砂岩时，锚杆长度由l=2 400 mm减少到l=2 000 mm。结果表明围岩的位移变形量减小，由此可知适当减小支护过程中锚杆长度，有助于减少巷道支护关键工序的时间，故巷道周边围岩条件不同时，适当减小锚杆长度不仅受力合理，而且节约材料，具备实际的经济价值。