基于屈服等值线模型的巷道冲击地压发生判断
孙中光
(1.瓦斯灾害监控与应急技术国家重点实验室,重庆 400037;2.中煤科工集团重庆研究院有限公司,重庆 400039;3.重庆大学 煤矿灾害动力学与控制国家重点实验室,重庆 400044)
冲击地压问题是困扰采矿与岩石工程界的一个突出问题,随着我国矿山开采深度和开采强度不断加大,矿井冲击地压危险也日趋严峻和复杂[1-5]。业内学者先后提出了一系列冲击地压触发理论,主要包括强度理论、刚度理论、能量理论、冲击倾向性理论、“三准则”理论、“三因素”理论、失稳理论及动静载荷叠加理论等[6-15],分别从不同角度对冲击地压发生的条件和过程进行了系统的研究和论证。其中,姜耀东等[5]建立了煤矿冲击地压的3种力学模型,即材料失稳型、滑移错动型和结构失稳型冲击地压。由于冲击地压发生机理复杂、影响因素较多,目前针对冲击地压的发生及防治机理的认识仍然不够深入,冲击地压事故依然时有发生。
笔者基于材料失稳型冲击地压发生的特点,以煤岩石屈服为研究对象,建立巷道受力力学模型,通过屈服准则解释巷道的围岩由弹性向塑性转化的趋势过程,得到巷道冲击地压发生的参考判断方法。
1 双屈服等值线模型分析
1.1 屈服应力场分析
考虑煤矿层状沉积岩覆岩的特性和顶底板的摩擦约束作用,选取矩形巷道侧壁为研究对象,将巷道侧壁简化为端部受约束的压缩体,半无限大板受力示意图如图1所示(图中θ为任意点A和荷载作用点连线与荷载方向的夹角,(°);L为荷载作用点间的距离,m;l为板厚(巷帮煤柱高度),m;r1、r2分别为任意点A与荷载作用点连线长度,m)。

图1 半无限大板受力示意图
端部约束可以认为集中力P作用于巷道上下两端,采用Airy应力函数计算。
表示A点受力的Airy函数Φ如下:
(1)
A点各应力分量如下:
(2)
采用莫尔圆将极坐标转换为直角坐标,则x、y方向上的应力如下:
(3)
若2个集中应力的负载相同,则2个集中应力可以采用弹性力学叠加原理,对式(3)进行转化,笛卡尔坐标系中点A的应力如下:
(4)
巷道开挖后,煤体向掘进空间膨胀,假设顶、底板岩石具有相同的特征,因此修正应力使其在y=0时,使应力σx一集中力分量为常数,并调整参数2P/πl。为满足应力量纲的常量Q,引入系数QA表示竖直方向的压缩力σy,A为无量纲系数,则式(4)可改写为:
(5)
1.2 屈服趋势分析
假设煤体服从莫尔-库仑屈服准则,不平衡力F的屈服函数可以表示为:
(6)
式中:σ1为中间主应力,MPa;σ3为围压,MPa;C为黏聚力,MPa;φ为内摩擦角,(°);K为判别因子。
当不平衡力F≥K时,煤体将发生屈服破坏,而K值取决于材料本身的性质。将σx、σy和τxy代入式(6),可得:
AQ≥K=2Ccotφ(1-sinφ)-1
(7)
将有关参数值代入式(7),计算得到屈服函数等值线如图2所示(不平衡力F范围0.0~1.0,F为1.0时表示达到屈服极限)。

(a)φ=40°, C=3.2 MPa
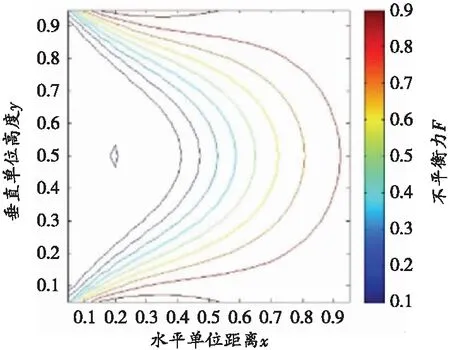
(b)φ=37°, C=(2.4x)MPa
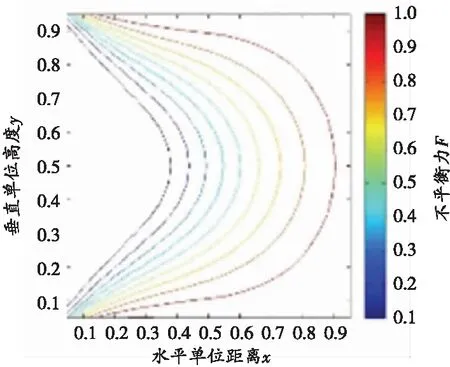
(c)φ=40°, C=(2.4x)MPa
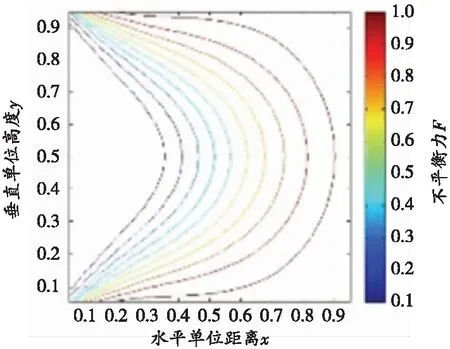
(d)φ=45°, C=(2.4x)MPa

(e)φ=50°, C=(2.4x)MPa
若竖直应力为均布荷载(即C=3.2 MPa),内摩擦角φ取40°,将C值代入式(7),用Matlab计算屈服函数F在笛卡尔坐标系里呈现出类双曲线的形式,如图2(a)所示,可以看出,屈服函数等值线最大F值出现在靠近巷道外缘的部分,说明煤体在受力过程中会由外到内逐层破坏。
在煤矿地应力实测中,最大水平主应力为竖直应力的1.2~2.0倍[16-18](以1.5倍为例),式(5)中水平应力取值为(0,2Q)。巷道或工作面中实测竖直应力集中系数取2.0~4.0(以3.0为例),假设在应力增高区域的垂直应力呈线性逐渐升高,校正系数取为0.6,故C值为:
C=2÷1.5×0.6×3x=2.4x
(8)
将式(8)计算值代入式(7),内摩擦角φ取37°,用Matlab计算屈服函数F在笛卡尔坐标系里等值线如图2(b)所示,可以看出,屈服函数等值线最大F值出现在巷道的深部,说明煤岩由深至浅破坏,煤岩浅部完整,最终巷道侧壁外缘完整块体突然剥离。
内摩擦角φ取值分别为40°、45°、50°,C值由式(8)确定,其屈服函数等值线如图2(c)~(e)所示。由图2(c)~(e)可知,随着内摩擦角φ的增加,其屈服函数等值线逐渐向深部移动,屈服函数等值线最大F值也在增大,这也印证了冲击地压多发生在硬岩或是硬煤巷道的规律。同时,由式(7)可知,围岩的内摩擦角φ值越大,冲击地压发生的位置越深、能量释放越强,造成的内部损伤也越严重;围岩的黏聚力C值越大,破裂面越靠近深部。
2 屈服等值线的实验验证
为验证屈服等值线的意义,运用有限元数值模拟软件模拟塑性区域的分布,并通过室内实验观察塑性变形带的形成。
2.1 端部约束压缩实验
实验设备选用重庆大学MTS815.03 电动液压伺服岩石实验系统,煤样取自天安煤矿(属冲击地压矿井),被加工成∅50 mm的标准圆柱型试样,以0.2 mm/min恒定速率加载。在试样端部采用卡箍固定,以模拟顶底板位移约束。煤样破坏过程如图3所示。

图3 煤样破坏过程
由图3可知,在加载过程中煤样破坏呈现阶段性特征:①弹性阶段煤样应力呈线性缓慢增长,在约达到其抗压强度的60%时,有少量的煤弹射出来,如图3(b)所示;②随着应力增大煤体继续变形,当应力达到抗压强度的78%左右时,煤体再次冲出,煤量较大,并伴随着明显的响声,如图3(c)所示;③随后煤体逐渐由内向外鼓出,但冲击现象并不明显;④当应力达到峰值强度时,煤体中心部分出现斜剪裂纹,其破裂面基本呈现出双曲线形状,如图3(d)所示。图3(d)与图2(a)所示情况非常相近。
2.2 煤体破坏趋势数值分析
采用COMSOL Multiphysics 4.4平台进行数值模拟,选用莫尔-库仑屈服准则和Prandtl-Reuss增量方程,验证内应力数值不均衡的情况。
计算区域内塑性应变分布如图4所示(红色区域表示塑性应变大,蓝色区域表示塑性应变小)。
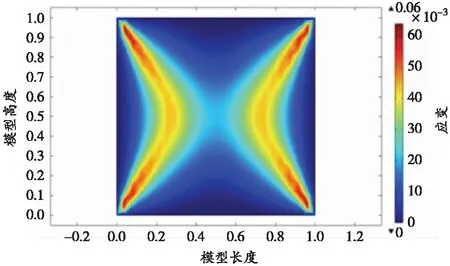
(a)矩形材料模型

(b)巷道模型
以煤体为矩形材料模型(煤体端部受到约束,竖直应力在矩形的中心较大,周边稍小)的塑性应变分布结果如图4(a)所示,模型大小为1.0×1.0。由图4(a)可发现明显的双曲线形态的塑性区域分布,且在矩形尖部有较大的塑性变形累计,并逐步将煤体以三角形块体整体形式切离。
上覆20 MPa压力下巷道开挖后塑性变形情况如图4(b)所示,模拟巷道尺寸为1.0×1.0。由图4(b)可知巷道的两帮有类似的双曲线塑性变形分布,与应力分析得到的图2(b)屈服函数等值线吻合。
3 现场观测验证
在冲击地压发生前,巷道会出现逐渐增大的鼓胀现象(如底鼓或帮鼓),直至发生突然失稳[16-17]。在巷道侧壁,竖直应力逐渐由均匀荷载变为内大外小的状态;在水平方向上,围岩逐渐向巷道空间膨胀,但受到端部约束的影响越来越大,当形成如图2(b)所示工况时,围岩深部将形成一条贯通内外的屈服等值线。因此,可通过对巷道围岩鼓胀量的判断来表征约束应力的发展情况,也可以此判断深部屈服等值线的发展情况;反之,通过对最大弹性鼓胀量计算也可以表征巷道冲击地压发生的临界状态。
一些典型冲击矿井发生冲击地压后的现场情况如图5所示。

图5 典型冲击矿井发生冲击地压后现场照片
由图5可知,冲击地压发生后,巷道煤壁一侧呈现出内凹的表面形状和冲出岩体的三角形岩块,与理论分析和试验模拟结果相吻合。
4 结论
1)通过巷道力学模型模拟得到的应力状态和双曲线形式的屈服等值线,若屈服等值线数值由外至内逐渐增大,则表明围岩深部破裂会导致煤岩体发生冲击。
2)围岩的内摩擦角越大,冲击地压发生的位置越深、能量释放将越强;围岩的黏聚力越大,破裂面越靠近深部。
3)室内单轴压缩实验表明,煤体破坏具有阶段性特征,且由外到内逐层破坏,最终破裂面基本呈现双曲线形状。
4)当竖直应力由外向里逐渐增大时,煤岩体内部容易形成明显的塑性变形带,从而诱发冲击地压。

