可解释性旅游需求量预测模型综述
王馨玉
(西安石油大学 计算机学院, 西安 710065)
0 引 言
随着社会的发展,越来越多的人选择出门旅游。对于城市、景区、酒店而言,需要依据淡旺季、客流量等因素调整规划和安排。因此,准确预测旅游需求量显得至关重要。
目前有很多的旅游需求量预测模型,但可解释性高的旅游需求量预测模型更值得信赖,也更有可能被有关部门所采纳。对于旅游规划者而言,探索出最影响旅游规划统筹的因素是非常重要的。通过对模型应用的解释,找出对旅游量影响的最主要的因素,从而制定出更好的旅游规划。对于模型开发者而言,模型的可解释性有助于在特定的情况(如过拟合等)下对模型进行修改。因此,本文针对旅游需求量预测模型进行了研究。
1 预测模型
1.1 时间序列模型
时间序列模型解释了一个关于其自身过去的变量和一个随机干扰项,探索所涉及的时间序列的历史趋势和相关因素(如季节性),并根据模型中确定的趋势和因素预测该序列的未来。
在使用时间序列预测技术的研究中,超过2/3的研究使用了不同版本的ARIMA模型。根据时间序列的频率,可以是简单的ARIMA,也可以是季节性的ARIMA。由于季节性是旅游业的一个主要特征,因此决策者对旅游需求的季节性变化非常感兴趣,所以在近几年中,季节性的ARIMA来越受欢迎。关于ARIMA和SARIMA模型的预测性能,实证研究提供了相互矛盾的证据。例如,ARIMA模型在所有情况下都优于AR模型和MA模型。SARIMA模型优于ARIMA、ARMA等其他8种时间序列方法,而非季节性ARIMA模型的性能高于所有考虑的预测模型的平均值。
1.2 其他预测模型
与时间序列模型相比,计量经济学方法的主要优势之一在于能够分析旅游需求(因变量)及其影响因素(解释变量)之间的因果关系。计量经济学分析“除了作为一种产生预测的工具之外,还发挥了许多有益的作用;例如,这些模型巩固了现有的关于经济如何运作的经验和理论知识,为渐进的研究战略提供了框架,并有助于解释其自身的失败”。就旅游需求而言,计量经济学分析从经济学家的角度解释旅游需求变化、证明政策建议以及评价现有旅游政策的有效性等方面具有实证意义。相反,在企业和政府主要关注的情况下,时间序列模型对于旅游需求和其他相关因素之间相互依赖的关系是没有帮助的。
粗糙集方法通过结合经典集理论对不精确、不确定或不完整的知识(数据)进行分类分析,是一种决策规则归纳法,用于对一组混合的数值变量和非数值变量之间的关系进行建模。它在旅游需求分析中的应用分别用于旅游购物、餐饮和观光支出分析。与经典的回归模型不同,粗糙集方法非常关注人口特征等分类变量,并根据这些变量之间的模型关系,预测与每个人口类别相关的旅游需求水平(而不是精确值),因此被认为是从微观角度分析旅游需求的计量经济模型的一个有用的补充工具。
模糊时间序列法在分析具有有限观测值的短时间序列时具有优势。灰色理论同样关注模型的不确定性和信息不足。研究者将模糊时间序列和灰色理论应用于旅游需求预测,利用模糊时间序列、灰色模型和马尔科夫修正灰色模型等三种模型,仅利用12项年度数据,对香港、德国和美国赴台旅游人数进行建模和预测。模糊时间序列模型预测性能的一致性有待进一步研究。
遗传算法(GAs)是基于自然选择和遗传进化思想的自适应、启发式搜索算法,通常被认为是一种优化方法。大量研究表明 , GAs适合解释旅游需求构成的变化。支持向量机(SVM)是另一种可用于解决分类、非线性回归估计和预测问题的人工智能技术[1]。
2 旅游需求量预测模型
2.1 建立预测模型
为了实现对时间维度和数据特征的可解释预测,本文开发了一个两阶段CNN架构。第一阶段是一个卷积层和一个k×1维卷积滤波器,学习过滤器识别出的,出现在不同情况下的重要的行为模式;第二阶段是一个1×1维卷积滤波器,可用于最先进的网络,如应用于最初的模型中,将第一阶段生成的特征映射的数量减少到1,即可以在第二阶段使用一维卷积。一维卷积使用的滤波器大小为k×n,其中n是特征数。使用一维过滤器可以提取所有特征中出现的重要行为模式。
通过这两个阶段,在网络模型中保持了多元时间序列的时间和空间动态,基于梯度的方法来生成显著性图,也称为属性图,以提取网络的注意力,可以认为它与对时间间隔和特征的预测最相关。
使用grad-CAM方法生成属性图。分别对产生fmaps=[f2d,f1d]特征图的两个阶段的最后一层应用grad-CAM,对于每个通用特征映射A上的每个激活单元u,获得一个与特定类输出c相关联的重要性权重wc,计算输出分数yc相对于A的梯度,对A进行全局平均,公式(1):
(1)
其中,Z为a的单位总数,在二维情况下,激活单位u为二维坐标{i,j}。
使用wc计算c类所有特征映射之间的加权组合,使用ReLU来删除负面影响,公式(2):
(2)
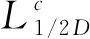
2.2 模型的可解释性
一些模型本身是具有可解释性的,如线性模型、决策树等。而很多机器学习模型是不具备可解释性的,对不可解释性模型的解释需要通过可解释性模型,即用可解释性模型去模拟拟合不可解释性模型。
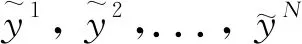
模型拟合过程如图1所示。
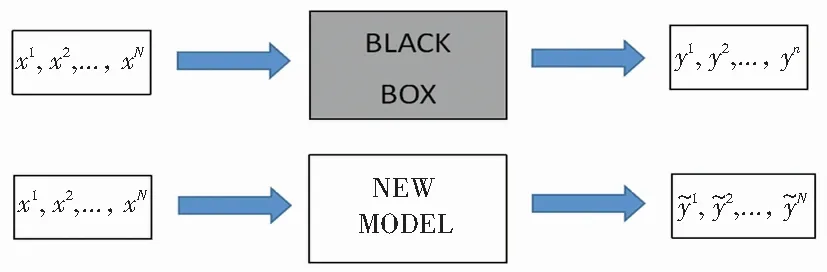
图1模型拟合
无法用一个新模型去完全地模拟黑盒模型的行为,只能用新模型模仿一部分黑盒模型的行为。LIME模型的原理如图2所示。
(1)找出一个待解释的数据点;
(2)在该数据点的附近进行数据点的取样;
(3)训练一个新模型使其可以模仿这个黑盒模型在样本点这个区域内的行为;
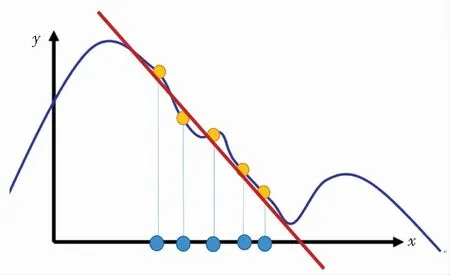
图2 LIME方法
3 结束语
可解释性是指人能够理解模型在其决策过程中所做出的选择,例如怎么决策、为什么决策和决策了什么,模型的可解释性对于相关单位解释模型的每一个决策至关重要。本文综合探讨了常见的旅游需求量预测模型以及模型的构建及其可解释性。有关单位提供的数据通过可解释性模型预测出的可解释性的数据,能够使这些单位更加具有针对性的做出决策(如旅游淡旺季分别开设旅游大巴数量、门票设置、安保人员设置等等),模型的可解释性研究将进一步发展,今后会为有关单位反馈更加精准的决策数据。

