基于有限元法及遗传算法的推力杆球铰多目标优化方法*

柯 俊，祖洪飞，史文库

（1.浙江理工大学，浙江省现代纺织装备重点实验室，杭州 310018； 2.吉林大学，汽车仿真与控制国家重点实验室，长春 130022）

前言

推力杆是商用车底盘系统中广泛应用的关键零部件，用于传递车桥与车架之间的纵向、侧向载荷及部分转矩，可使车桥传来的部分振动能量衰减。在推力杆服役过程中，其球铰中的橡胶衬套经常发生疲劳破坏，这将导致商用车底盘系统的导向功能部分失效，从而严重威胁行车安全。要显著提升推力杆球铰的疲劳寿命，除了提升橡胶材料的力学性能外，还须对其球铰结构进行针对性的优化设计。然而，推力杆的球铰结构复杂，球铰中的橡胶衬套不但具有变截面特征，而且其变形也具有非线性。此外，橡胶衬套被金属外套包裹，因此无法观察橡胶衬套的实际失效过程，使推力杆球铰的性能优化变得非常困难。目前，已有学者对推力杆球铰应力进行分析［1］，对推力杆纵向刚度优化方法［2］及修正方法［3］和疲劳寿命预测方法［4］进行了深入研究。然而，相关研究仍然无法为推力杆的球铰结构优化提供理论和方法指导，导致推力杆的球铰设计具有一定的盲目性。

要科学地优化推力杆的球铰结构，需解决如下关键问题：准确理解橡胶衬套的失效机理；确定球铰结构参数与性能参数之间的关系；针对性地建立球铰结构优化模型，并通过优化设计显著提高球铰的疲劳寿命。由于橡胶部件的刚度不仅影响其疲劳寿命［5-7］，而且影响整车性能［8］，因此，应在优化球铰应力应变分布状态的同时，兼顾其刚度特性［9-10］。此外，橡胶结构具有非线性和变截面特征。因此，有限元分析是实现橡胶结构优化的基本途径［11-12］。随着研究的深入，综合利用有限元法和遗传算法完成橡胶部件的优化设计取得了成功［13-14］，这为推力杆球铰的优化设计指明了方向。

本文中首先进行球铰失效机理分析和球铰刚度影响因素分析，然后基于有限元模拟结果与遗传算法建立了推力杆球铰结构的多目标优化模型，并进行了优化设计，结果表明，推力杆球铰的疲劳寿命显著提高，从而为推力杆球铰的优化设计提供了理论依据。

1 推力杆结构与失效模式

本文中所研究推力杆的安装状态和球铰疲劳破坏形式如图1所示，主要表现为大端头球铰橡胶衬套的疲劳失效。推力杆球铰的内部结构如图2所示。在球铰内部，橡胶衬套通过硫化的方式与端盖、芯轴、塑料层和金属外套固连。塑料层与芯轴之间为间隙配合，为橡胶衬套提供用于应力释放的旋转自由度。压缩预应力能促进橡胶材料疲劳裂纹的闭合，有助于提高橡胶衬套疲劳寿命。由于橡胶衬套自身也具有一定的过盈量，所以在装配过程中会产生一定的预压缩量。

图1 推力杆的安装状态及球铰的疲劳破坏形式

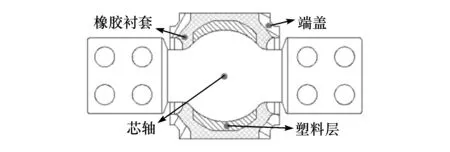
图2 球铰内部结构示意图

影响橡胶衬套疲劳寿命的因素主要包括外部载荷、橡胶材料力学性能、环境温度、球铰结构和橡胶衬套预压缩量。受安装环境和成本限制，只有优化球铰结构和调整预压缩量在工程实际中是可行的。

图3 在ABAQUS软件中建立的推力杆有限元模型

2 球铰失效机理

为使球铰结构优化更具针对性，须对推力杆原结构进行有限元模拟，并获取橡胶衬套的变形状态，进而分析推力杆球铰的失效机理。基于前期研究［1-3］建立的推力杆有限元模型如图3所示。其中，橡胶材料的本构模型采用2阶Ogden模型，泊松比设置为0.492。推力杆纵向刚度的有限元模拟值为57.63 kN／mm，试验值为58.78 kN／mm，刚度误差小于2%。同时，根据模态分析结果，模型1阶模态频率与样件1阶模态频率之间的误差为6.3%。由此可知，建立的推力杆有限元模型正确，且仿真精度满足要求。

模拟得到的推力杆球铰原结构在不同外部载荷作用下的变形状态如图4所示。根据图4（b），在承受150 kN纵向拉伸载荷后，橡胶衬套环面一侧产生了压缩变形，而另一侧产生了拉伸变形（图中矩形标识区域），且受压侧的橡胶被迫向球铰外侧延展（如图中箭头标识所示方向）。由于橡胶衬套与芯轴及端盖等金属件之间的硫化粘接对橡胶衬套的延展变形起到了约束作用，因此橡胶衬套端部的压缩侧产生了最大的拉伸变形，疲劳初始裂纹也将在该处产生。随着服役时间的增加，裂纹继续扩展，进而削弱球铰金属件对橡胶衬套延展趋势的约束作用，导致球铰整体刚度下降，使橡胶衬套环面的应变不断增大，最终橡胶衬套环面产生疲劳破坏，导致球铰疲劳失效。

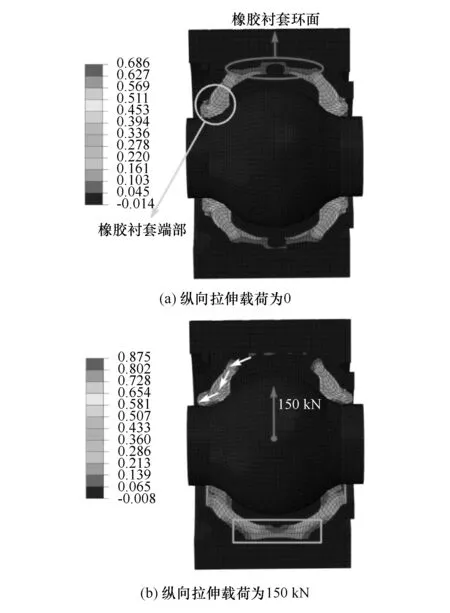
图4 承受不同纵向拉伸载荷时球铰的总体变形状态（图中量化参数为最大主应变）

3 球铰结构的多优化

根据球铰失效机理分析结果，提高橡胶衬套疲劳寿命的关键在于限制橡胶衬套端部的延展变形并降低橡胶衬套环面的变形量。由于橡胶材料具有非线性且橡胶衬套为不规则结构，因此橡胶衬套的变形量无法通过常规的数值计算方法准确量化。然而，在球铰内部空间和外部载荷一定的前提下，橡胶衬套端部延展变形量降低的宏观表现为推力杆球铰轴向刚度的增加，而橡胶衬套环面变形量降低的宏观表现为推力杆纵向刚度的增加。因此，可用推力杆球铰轴向刚度和推力杆纵向刚度来间接量化橡胶衬套的变形量。

3.1 球铰刚度影响因素分析

3.1.1 橡胶衬套预压缩量

球铰原结构橡胶衬套的径向预压缩量为2 mm，轴向预压缩量为5 mm。当橡胶衬套具有不同的径向预压缩量Sr和轴向预压缩量Sa时，通过有限元模拟得到的推力杆纵向刚度Kl和球铰轴向刚度Ka如图5所示。

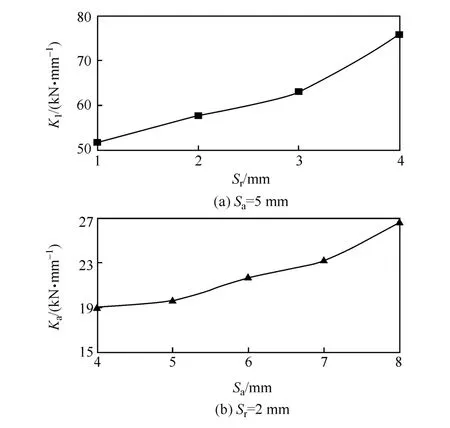
图5 不同橡胶衬套预压缩量下推力杆刚度参数的变化趋势

由图可见，随着橡胶衬套预压缩量的增大，推力杆的纵向刚度和球铰轴向刚度均明显增大。然而，过大的刚度会削弱推力杆的减振性能。因此，要保证推力杆刚度参数落在合理区间，须对橡胶衬套的预压缩量进行优化。

3.1.2 橡胶衬套体积

虽然橡胶衬套自由状态下的体积由预压缩量决定，但球铰中橡胶衬套的装配体积由球铰外套直径和塑料层的形状、宽度与厚度决定。通过有限元模拟得到的推力杆纵向刚度随橡胶衬套装配体积的变化情况如表1所示。

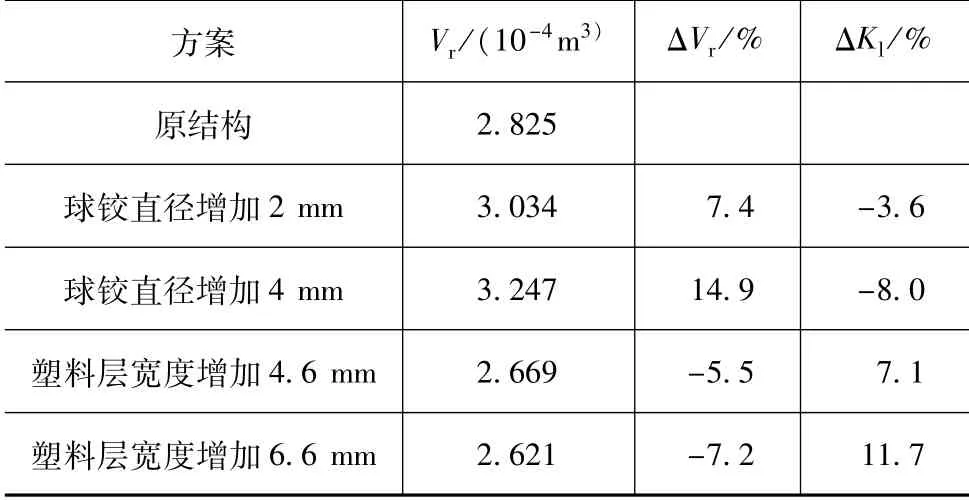
表1 推力杆纵向刚度随橡胶衬套装配体积的变化情况［2］

由表可见，推力杆的纵向刚度不但随着球铰直径的增大而减小，而且随着塑性层宽度的增大而增大。因此，减小橡胶衬套的装配体积可有效减小其变形。

3.1.3 橡胶衬套硫化面积

根据表1，当球铰直径增加2 mm时，橡胶衬套的体积变化率为7.4%，推力杆的纵向刚度减小3.6%。而当塑性层宽度增加4.6 mm时，推力杆的纵向刚度增加7.1%，几乎是3.6%的两倍。同时，对应橡胶衬套的体积变化率为5.5%，也小于7.4%。因此，增加塑料层的宽度对于提高推力杆纵向刚度方面具有更高的效率。这是因为增加塑料层的宽度不仅会减小橡胶衬套的安装体积，而且会增大橡胶衬套的硫化面积，从而加强了塑料层对橡胶衬套延展变形的约束作用。因此，增大橡胶衬套的硫化面积有利于推力杆疲劳寿命的提高。

3.1.4 塑料层表面形状

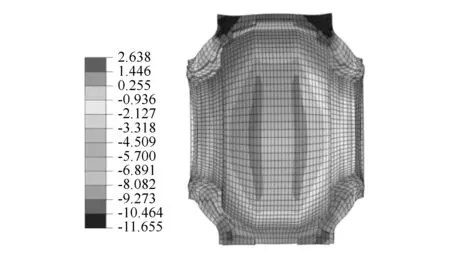
图6 橡胶衬套原结构拉伸侧的应力分布（图中量化参数为最大主应力）

理论上塑料层的表面形状可以有无数种设计方案。因此，应根据橡胶衬套的变形特点针对性地提出对塑料层形状的优化措施。橡胶衬套原结构在拉伸侧的应力分布如图6所示。根据图6，由于塑料层表面存在两条棱边，因此橡胶衬套环面产生了应力集中的现象。同时，根据图4（b），由于塑料层的表面形状为近似球形，因此，它不仅对橡胶衬套环面施加了纵向力，而且对橡胶衬套端部施加了轴向力。因此，塑料层表面形状的优化方案不仅要消除橡胶衬套的应力集中现象，还要尽量降低塑料层的轴向分力。

3.2 球铰结构的多目标优化

3.2.1 优化变量及基因编码

根据球铰刚度影响因素的分析结果，要降低球铰的变形量，不但要优化橡胶衬套的预压缩量、塑料层的形状和尺寸参数，而且还要保证推力杆的纵向刚度和轴向刚度满足载荷传递及减振的设计要求。优化模型中使用的塑料层的表面形状和相关变量如图7所示。

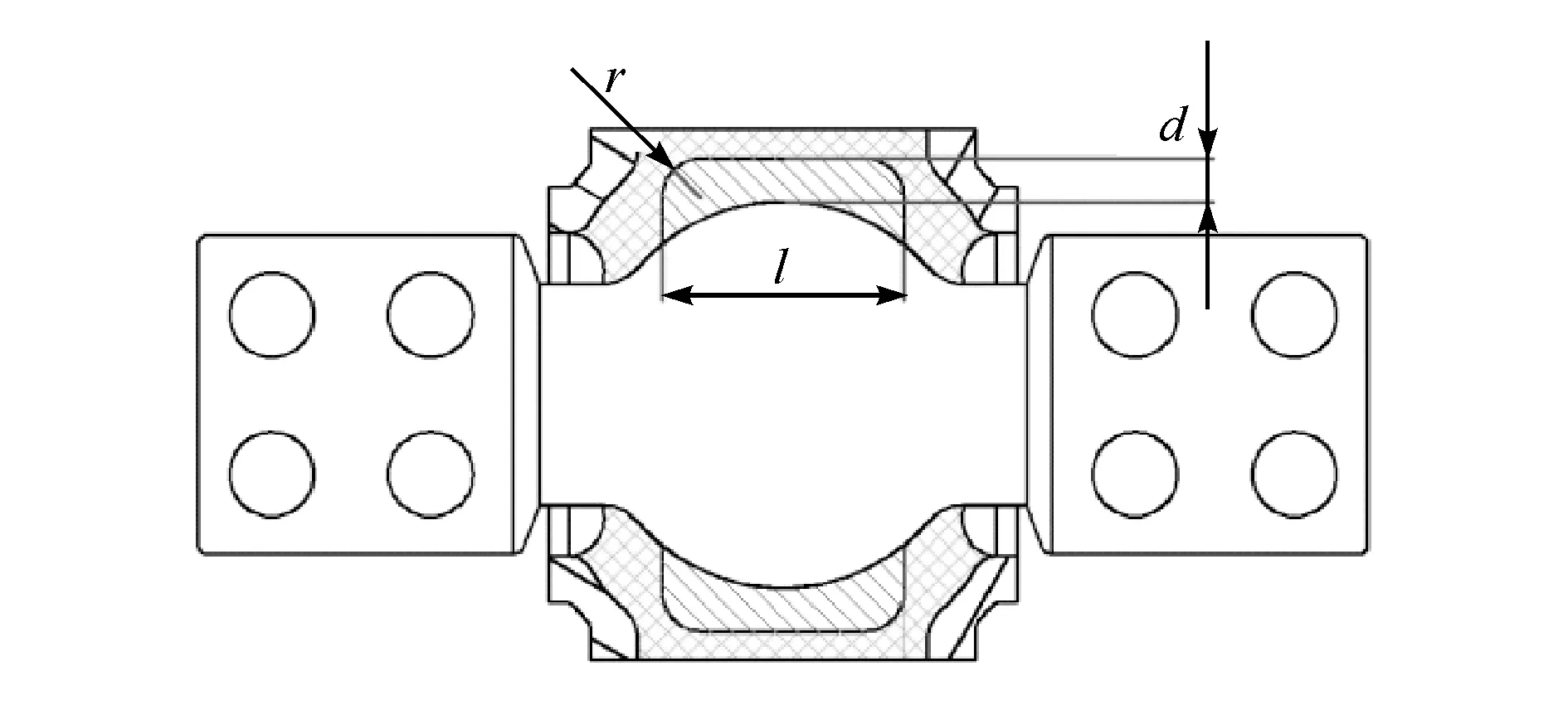
图7 优化模型中使用的球铰结构

图7中，塑料层表面形状为圆柱形，且在边缘设置了圆角。这种表面形状不仅消除了橡胶衬套的应力集中现象，而且最大程度降低了塑料层的轴向分力。受推力杆安装环境的限制，球铰的直径和宽度不宜变动。因此，橡胶衬套的体积取决于塑料层的厚度d、宽度l和塑料层圆角半径r。因此，选取的优化变量除了橡胶衬套的轴向预压缩量Sa和径向预压缩量Sr外，还包括上述3个变量。在优化模型中，一组5个优化变量的数值组合可以唯一地表征球铰的结构特征和性能，并对应于遗传算法中的某个个体。因此，选取的基因型是长度为5的双精度浮点数。

3.2.2 约束条件

为保证推力杆性能满足设计要求，并防止球铰内的运动干扰，优化模型的约束条件为

式中kr和ka分别为球铰的径向刚度和轴向刚度。设置λk的目的是使球铰径向刚度和轴向刚度的配比落入合理的区间。

3.2.3 适应度函数（目标函数）

塑料层的横截面积越大，则橡胶衬套的体积越小，且MATLAB遗传算法工具箱中规定罚函数值越小越优。因此，将考虑橡胶衬套体积优化的优化子目标函数定义为

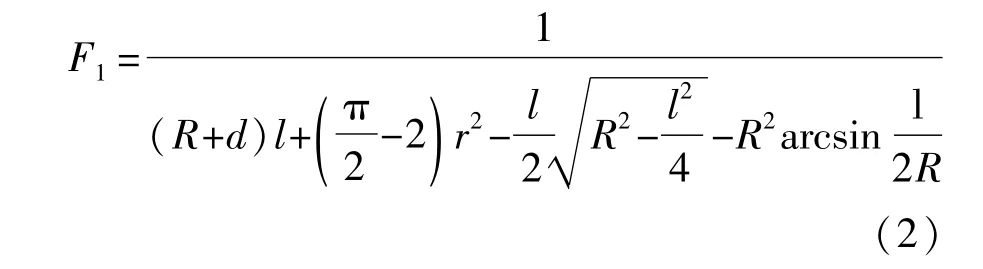
式中R为芯轴半径，R＝40 mm。

为得到球铰刚度参数与优化变量间的关系，利用有限元法计算了不同结构参数下球铰的刚度参数。基于大量计算结果，采用多元线性回归方法拟合了球铰刚度参数与优化变量间的数值关系：

则考虑球铰刚度优化的优化子目标函数定义为

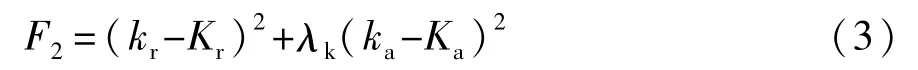
式中Kr和Ka分别为球铰径向刚度和轴向刚度的设计平均值，Kr＝80 kN／mm，Ka＝27 kN／mm。设计平均值代表理想的刚度特性，因此F2使得球铰的刚度特性落在合理范围，趋于理想刚度特性，且使进化方向偏向于增强球铰的轴向刚度，从而减弱橡胶衬套端部的延展趋势，抑制初始疲劳裂纹的产生。

此外，橡胶衬套的硫化面积也应最大，从而有效抑制橡胶衬套的延展趋势，并提高球铰的刚度。从橡胶衬套与塑料层、芯轴在球铰纵切面上的硫化粘结长度出发，定义硫化面积的优化子目标函数为

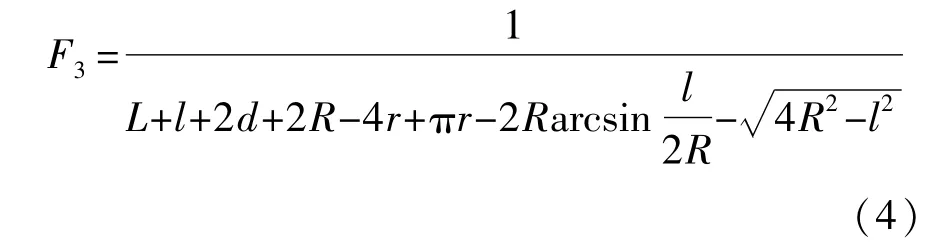
式中L为橡胶衬套与芯轴硫化区域的切面弧长，L＝85 mm。

3.2.4 优化结果

将F1、F2和F3作为各子种群的适应度函数，在MATLAB遗传算法工具箱中采用混合法进行优化计算，得到的优化结果如图8所示。

图中，刚度优化目标为式（3）的计算结果。最优解如图中的圆圈所示，对应球铰结构参数的最优组合为：Sr＝6.4 mm，Sa＝4.1 mm，l＝57.2 mm，d＝3.3 mm，r＝5.1 mm。

为方便批量生产和工程应用，将上述数值圆整，则球铰结构参数的优化方案为：Sr＝6.5 mm，Sa＝4 mm，l＝57 mm，d＝3 mm，r＝5 mm。

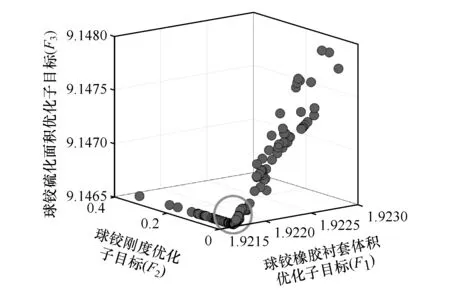
图8 通过遗传算法得到的最优解分布

3.3 优化效果分析

为预判优化方案的优化效果，对采用优化方案的推力杆进行有限元模拟。表2为球铰刚度优化结果与有限元模拟结果的对比。

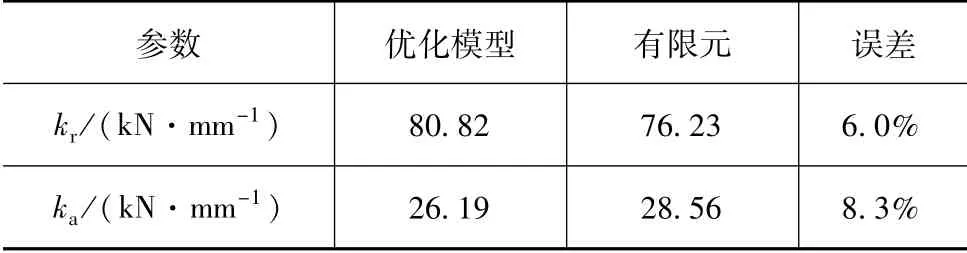
表2 球铰刚度优化模型计算值与有限元模拟值的对比

由表可见，两种方法得到的刚度值误差均小于10%。优化后橡胶衬套的应变分布如图9所示。根据有限元模拟结果，采用改进方案后，橡胶衬套的最大应变由0.875降低到0.747。橡胶衬套环面的应力集中现象也得到消除。因此，优化方案的优化效果良好。

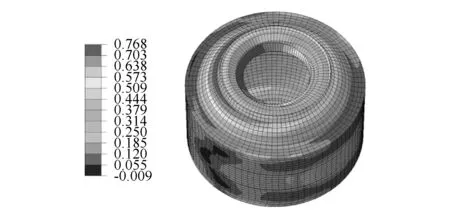
图9 采用优化方案后橡胶衬套的应变分布（图中量化参数为最大主应变）

4 试验验证

为验证优化方案的优化效果，对采用优化方案的推力杆样件进行纵向刚度试验和疲劳试验，如图10所示。在试验过程中，固定推力杆的两个小端头，对大端头球铰的芯轴施加峰值为150 kN、均值为0、频率为1 Hz的纵向正弦载荷。在加载过程中，根据需要，采集大端头球铰芯轴的位移和载荷数据，并通过风扇为球铰散热。试验结果表明，与原结构相比，改进后的推力杆样件纵向刚度由58.78提高至72.03 kN／mm，疲劳寿命提高了7倍。

图10 推力杆纵向刚度和疲劳寿命台架试验

5 结论

（1）提高推力杆球铰橡胶衬套疲劳寿命的关键在于限制橡胶衬套端部的延展变形并降低橡胶衬套环面的变形量。

（2）适当提高橡胶衬套的预压缩量，减小橡胶衬套的体积，提高橡胶衬套的硫化面积，优化塑料层表面形状，以消除橡胶衬套的应力集中并降低塑料层的轴向分力，这些措施均有利于推力杆球铰疲劳寿命的提高。

（3）提出的优化方案没有大幅度改变推力杆的原有设计方案，控制了改进成本，而且优化效果显著。说明提出的推力杆球铰结构多目标优化方法正确，而且适宜工程应用，这对完善推力杆的设计理论、保证商用车平衡悬架和轨道客车转向架的可靠性具有重要意义。