基于磁场重构法的轴向磁通轮毂电机建模研究

李 涛，张幽彤，梁玉秀，杨 业，艾 强

（北京理工大学机械与车辆学院，北京 100081）

前言

轮毂电机技术将电机固定在车轮内部，电机输出的动力直接作用在车轮上，具有传动效率高、转矩分配灵活、结构紧凑等优点［1-3］。轴向磁通永磁电机与传统径向磁通电机相比，具有功率密度大、效率高和轴向结构紧凑等优点，作为轮毂电机具有明显优势［4］。定子无磁轭模块化结构轴向磁通电机作为一种新型的轮毂电机，具有质量轻、损耗小的优点，有广阔的发展前景［5］。

快速准确地计算出电机的电磁特性是轴向磁通轮毂电机设计和优化的关键，轴向磁通轮毂电机特殊的三维结构使其无法像径向电机一样进行简单的二维有限元计算。三维有限元法［6］（FEM）可根据电机的实际结构尺寸，精确地计算磁场分布，但其计算耗时长，占用计算机资源多，通常用来验证其它计算方法的准确性。解析法［7］通常假设一组圆柱形切片穿过电机，并将切片展开成多个二维直线电机形式进行分析。该假设忽略了绕组的端部效应，并认为直线电机沿着径向方向的尺寸为常量，但实际上轴向磁通轮毂电机沿任何方向的尺寸都是变化的，特别是当永磁体采用斜极技术、定子齿采用斜槽技术或定转子沿径向方向尺寸不相等时，通过径向切片建模的方法无法满足精度要求。

磁场重构法（FRM）可利用少量的静态有限元计算获得电枢励磁和永磁体励磁时的气隙磁密分布，建立定子和转子的基础函数组，根据励磁电流的大小与转子位置的不同对气隙磁密进行重构，进而获得电机的电磁性能参数，包括电磁转矩、齿槽转矩和反电动势等，能避免电机等效模型不精确所带来的精度问题，同时可明显改善运算速度。目前，采用二维磁场重构法对不同类型径向磁通轮毂电机的电磁性能研究较为成熟。文献［8］～文献［10］中采用二维磁场重构法对永磁同步电机的转矩波动和径向电磁力波进行了研究。文献［11］中采用二维磁场重构法对感应电机的磁密分布和电磁力进行了计算。文献［12］中以转矩脉动为优化目标，提出了一种基于二维磁场重构法的双馈电机转子电流的优化方法。与径向磁通电机不同，轴向磁通轮毂电机具有三维结构特性，拓扑结构多，定转子数量也各不相同。文献［13］和文献［14］中采用三维磁场重构法对单定子单转子轴向磁通电机进行研究，计算了永磁体退磁、转子偏心等故障下电机的电磁特性。文献［15］中采用三维磁场重构法对考虑平行槽效应和永磁体伸出结构的单定子单转子轴向磁通轮毂电机进行了研究。与单定子单转子轴向磁通轮毂电机相比，定子无磁轭模块化结构采用双转子进行永磁体励磁，并去掉了定子轭，使电机的磁路结构、气隙数、绕组方式均发生了变化，三维磁场重构法在该类型电机上的应用还鲜有报道。本文中以一台基于非晶合金定子齿的无磁轭模块化轴向磁通轮毂电机为样机，采用三维磁场重构法对该轮毂电机的气隙磁密进行重构计算，结合麦克斯韦应力张量法对电磁力和电磁转矩进行计算，分析了磁链和反电动势波形，并与三维瞬态有限元法计算结果的精度和计算时间进行了对比。

1 轴向磁通轮毂电机结构

本文中以一台三相、24极、27槽的轴向磁通轮毂电机为研究对象，样机三维模型如图1所示。定子齿采用非晶合金材料1k101卷绕而成，齿顶部为开槽结构，横截面为空心圆形。图2为定子绕组和磁极的分布方式，绕组采用分数槽集中绕组，A、B、C为顺时针环绕，a、b、c为逆时针环绕，不同的箭头方向分别代表永磁体磁极的N极和S极。铁心与绕组之间注入环氧树脂，起到固定和绝缘的作用。永磁体采用钕铁硼材料N38EH，为减小齿槽转矩，永磁体采用圆形斜极，其位置通过转子背铁和转子支架进行固定，以防止永磁体在高速旋转时移动。定子支架、转子支架以及转子轴为不导磁材料，建模时忽略。电机主要的尺寸参数如表1所示，该电机由3个单元电机构成，每个单元电机为8极，9槽。

图1 样机结构简图

图2 绕组分布与磁极

表1 轴向磁通轮毂电机主要参数

2 轴向磁通轮毂电机的三维磁场重构法

2.1 算法简介与假设

三维磁场重构法以静态三维有限元计算结果为基础，通过静态求解器分别计算单元电机通入单位电流I0、单相电枢励磁时的气隙磁密和不同转子位置处永磁体励磁时的气隙磁密，将两者的计算结果分解为径向、切向和轴向气隙磁密分量Br、Bφ和Bz，如图3所示，并将这些气隙磁密分量作为基础函数组进行存储，然后利用基础函数组对任意励磁电流和转子位置下各向气隙磁密进行重构，获得气隙平面的合成磁密，进而计算电机的电磁转矩、电磁力和反电动势等电磁特性。

图3 电机转子和气隙磁密分量

建模时进行如下假设：

（1）忽略损耗与温升对电机的影响；

（2）电机工作在线性区域，定子齿和转子背铁的磁导率无限大，气隙磁密可线性叠加；

（3）忽略变频器产生的时间谐波电流；

（4）为方便基础函数组的存储，对气隙平面进行离散化假设。

图3中所示的气隙平面与非晶合金定子齿和永磁体的距离相等，该圆环面的内外径与转子的内外径相等。假设将气隙平面沿径向方向由内径Ri至外径Ro划分为M层，沿切向方向由0至2π／k划分为N段，每段弧长为2π／kN，k为单元电机数。因此，单元电机各向气隙磁密可通过M×N的阵列进行存储。如径向气隙磁密矩阵中第m行第n列的值用来表示半径为r、偏转角度为φ处的径向气隙磁密值。其中：

2.2 定子基础函数组

定子绕组产生的磁场是各定子槽电流励磁时产生的合成磁场。由于A相、B相和C相的电流是对称的，且B相和C相分别超前于A相2π／3和4π／3电角度，为提高计算速度，仅对单元电机单相绕组励磁时的气隙磁密进行计算，通过相移即可获得其他两相电流励磁时的气隙磁密。单相绕组励磁时的气隙磁密通过三维静态有限元法获得，建模时需忽略永磁体励磁。由于假设电机工作在线性区域，电流幅值的选取与定子基础函数组无关，为了方便计算，设置初始励磁电流I0为1 A。样机采用表贴式永磁体结构，永磁体的磁导率与空气的磁导率接近，可认为定子绕组产生的气隙磁密不受转子位置的影响。将单位电流励磁时引起的单元电机径向、切向和轴向气隙磁密作为定子基础函数组，分别用hrs、hφs和hzs表示：

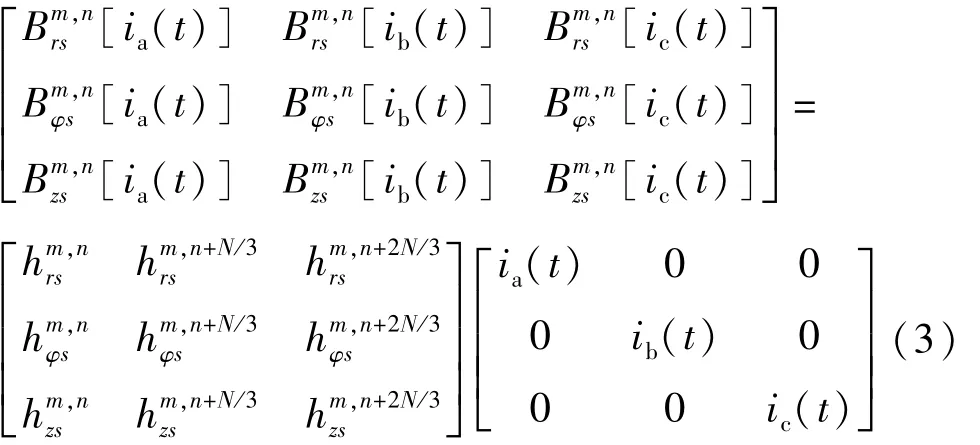
式中：Brs、Bφs和 Bzs分别为电枢励磁时沿径向、切向和轴向的气隙磁密分量；ia、ib和ic分别为三相电流。计算可得单相绕组励磁时单元电机的气隙磁密云图，如图4所示，提取气隙磁密时须通过式（4）和式（5）将直角坐标系下的气隙磁密Bx和By转换为沿径向和切向的柱坐标系下的气隙磁密Br和Bφ并存储。

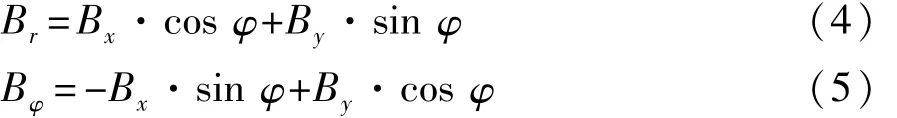
2.3 转子基础函数组

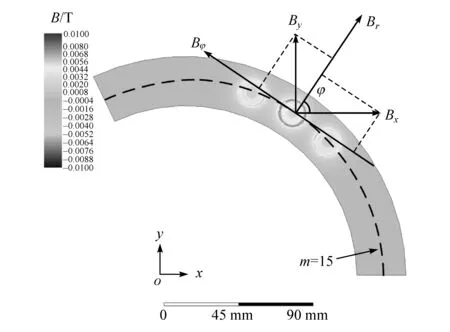
图4 单相电流励磁时的气隙磁密云图

由于非晶合金材料具有硬、脆、薄的物理特性，不易对定子齿顶部进行加工，通常设计为开槽结构。因此，建立转子基础函数组时必须考虑定子的开槽效应，须通过三维静态有限元法获得不同转子位置θr处的气隙磁密。设置定子的三相绕组均为开路状态，永磁体励磁时的转子基础函数组和可表示为

式中：BrPM、BφPM和BzPM分别为永磁体励磁时沿径向、切向和轴向的气隙磁密分量；q为转子旋转系数。转子位置θr的表达式为

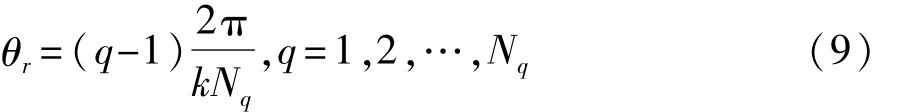
式中Nq为转子旋转位置数。提取不同转子位置处单元电机永磁体励磁时的气隙磁密并进行存储，当θr＝0时的气隙磁密云图如图5所示。

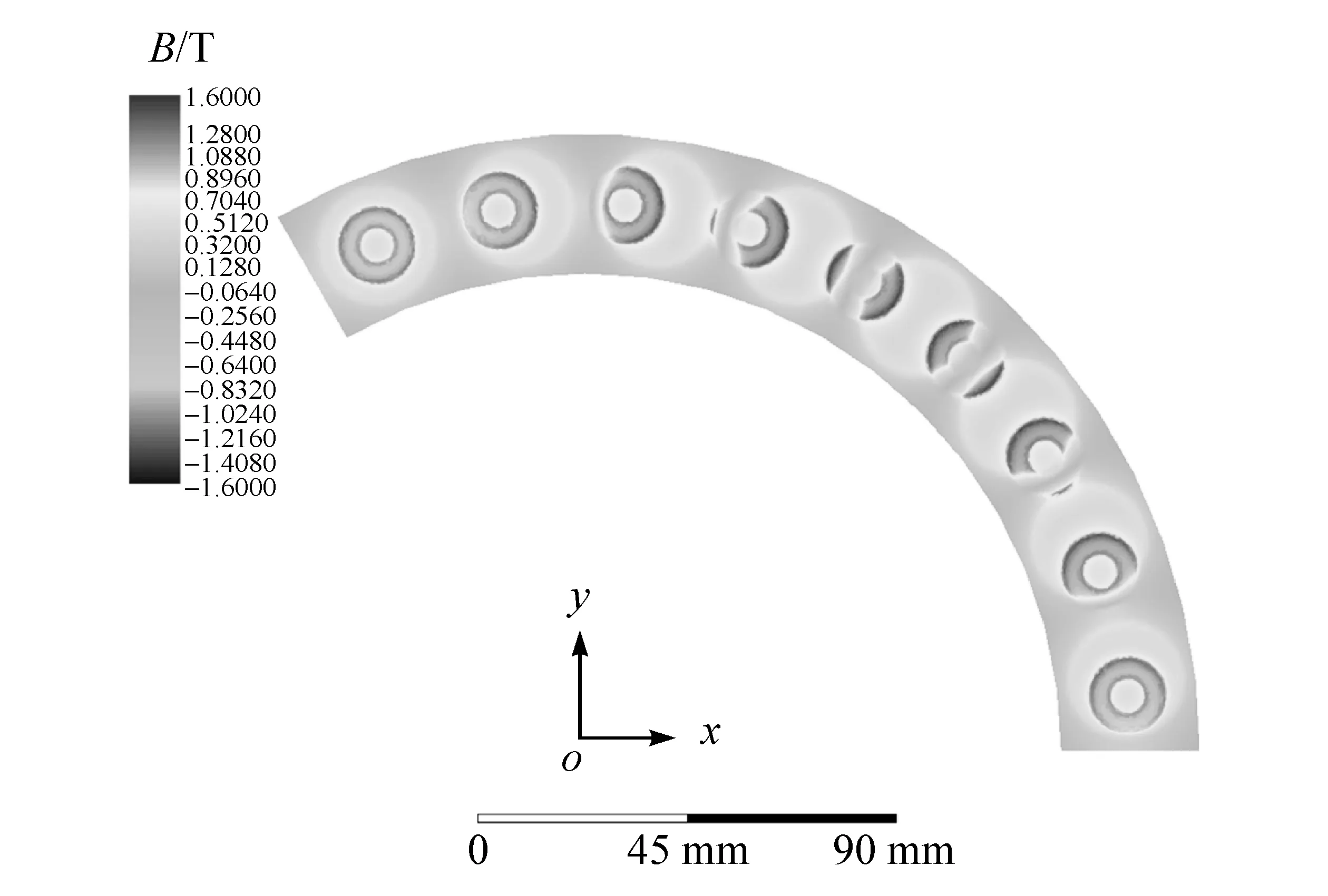
图5 永磁体励磁时的气隙磁密云图

2.4 气隙磁场重构

三维磁场重构法的算法流程图如图6所示。由已存储的定转子基础函数组通过线性叠加分别获得单元电机沿径向、切向和轴向的磁密分量Br、Bφ和Bz，可表示为

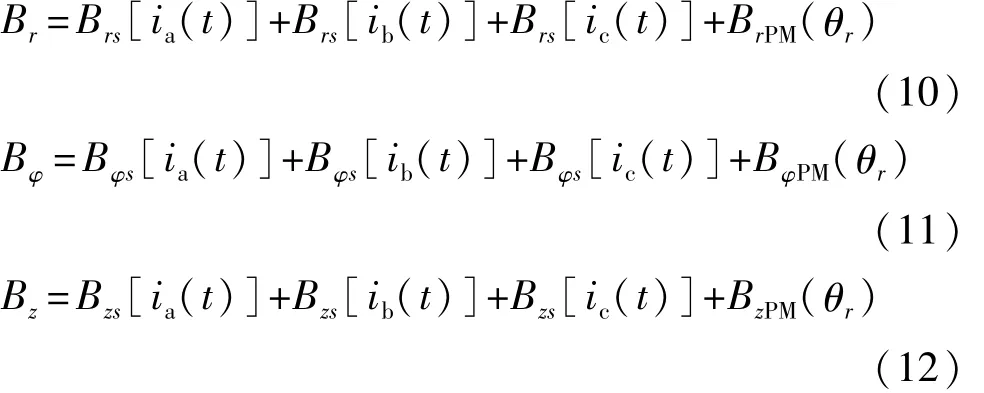
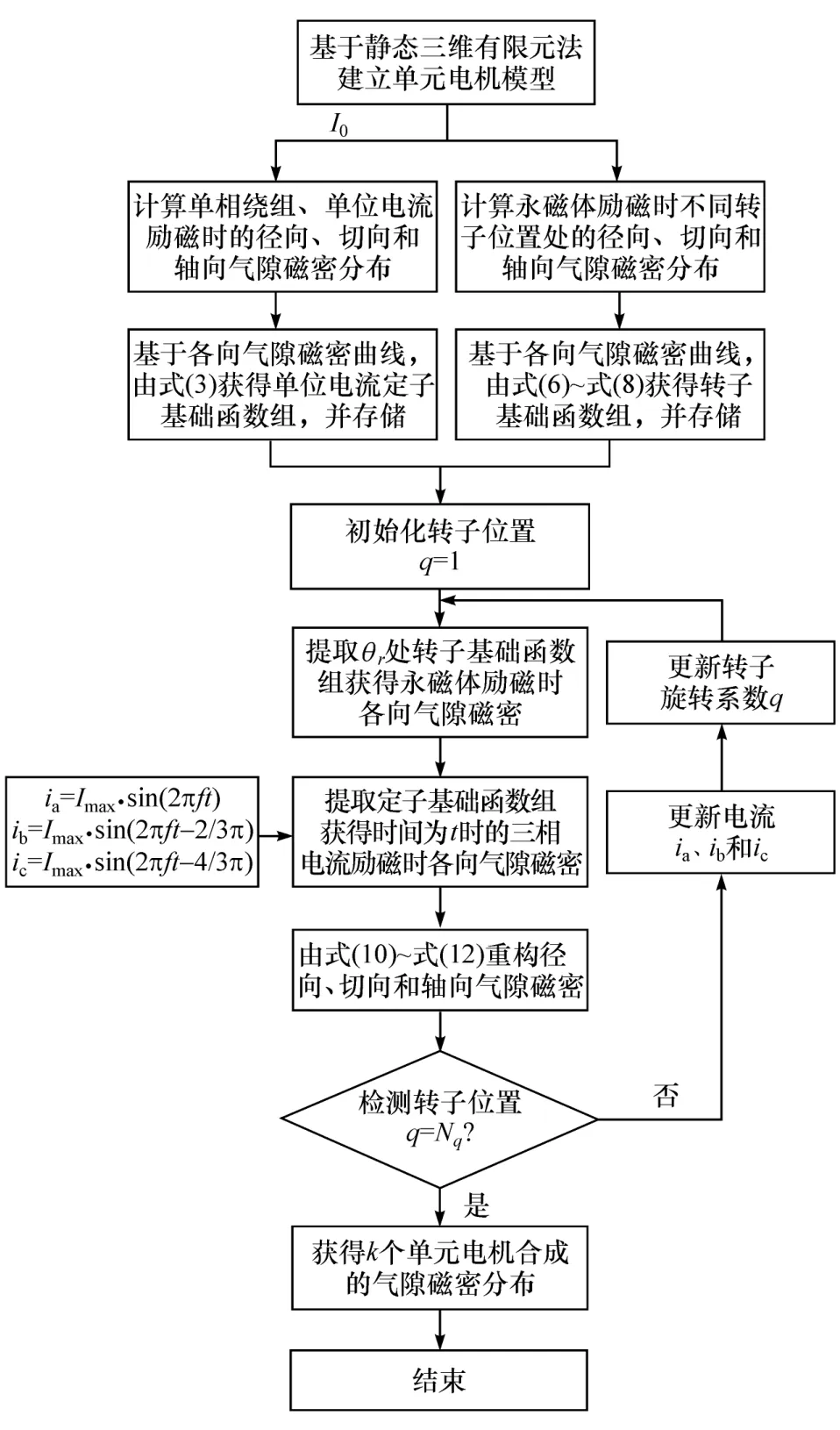
图6 三维磁场重构法流程图

图6 中的Imax和f分别为励磁电流的幅值和频率，在每一个电周期内选取Ni个时间点进行计算，其取值必须满足励磁电流波形要求。为了保证转子位置θr和励磁电流时间t同步更新，转子旋转位置数Nq和单位电周期内时间点选取数Ni应当满足如下关系：

2.5 电磁力与转矩计算

麦克斯韦应力张量法是用等效的面积力代替体积力的一种方法。将磁场重构后的气隙磁密计算结果带入麦克斯韦张量方程，即可得到单侧气隙的电磁力密度沿径向、切向和轴向的分量fr、frφ和

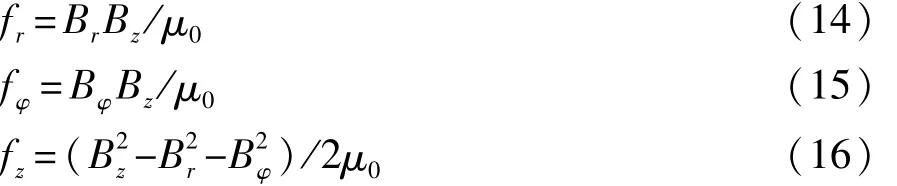
式中μ0为真空磁导率，其值为4π×10-7H／m。由式（14）～式（16）可求出离散化后气隙平面内任意一个子面域的三向电磁力密度。径向电磁力Fr由绕组端部与永磁体相互作用而产生，可认为是转子的内应力，通常用来校核转子支架强度。沿轴向的单侧转子电磁力Fz可表示为

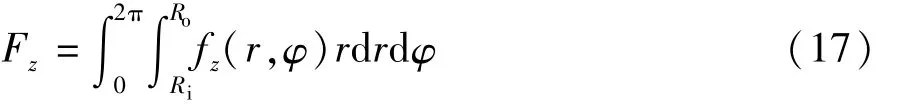
轴向电磁力Fz产生轴向不平衡磁拉力，通常用来校核轴承的轴向载荷，由于样机采用双转子结构，定子上受到的轴向电磁力合力为零，转子上受到的轴向电磁力通常较大。

切向电磁力Fφ产生电磁转矩Te，通过转子轴直接作用于车轮上。针对定子无磁轭模块化结构双转子双气隙特点，电磁转矩Te的表达式为

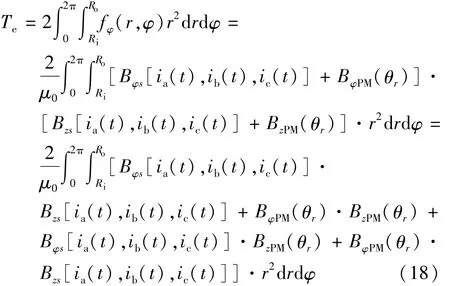
由于定子和转子无法单独产生电磁转矩，式（18）可简化为

当电机空载时，齿槽转矩Tcog可表示为

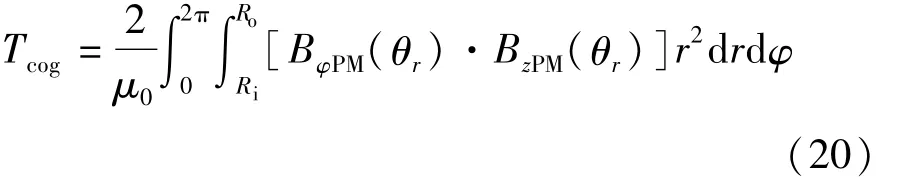
2.6 磁链与反电动势计算

进入定子齿的磁通线大多数会通过图7中设定的气隙平面，少量的磁通线会通过定子齿的齿间传递而不经过气隙平面，忽略这一部分齿间传递，通入单相电流时定子的磁通量可以通过气隙磁密进行计算。

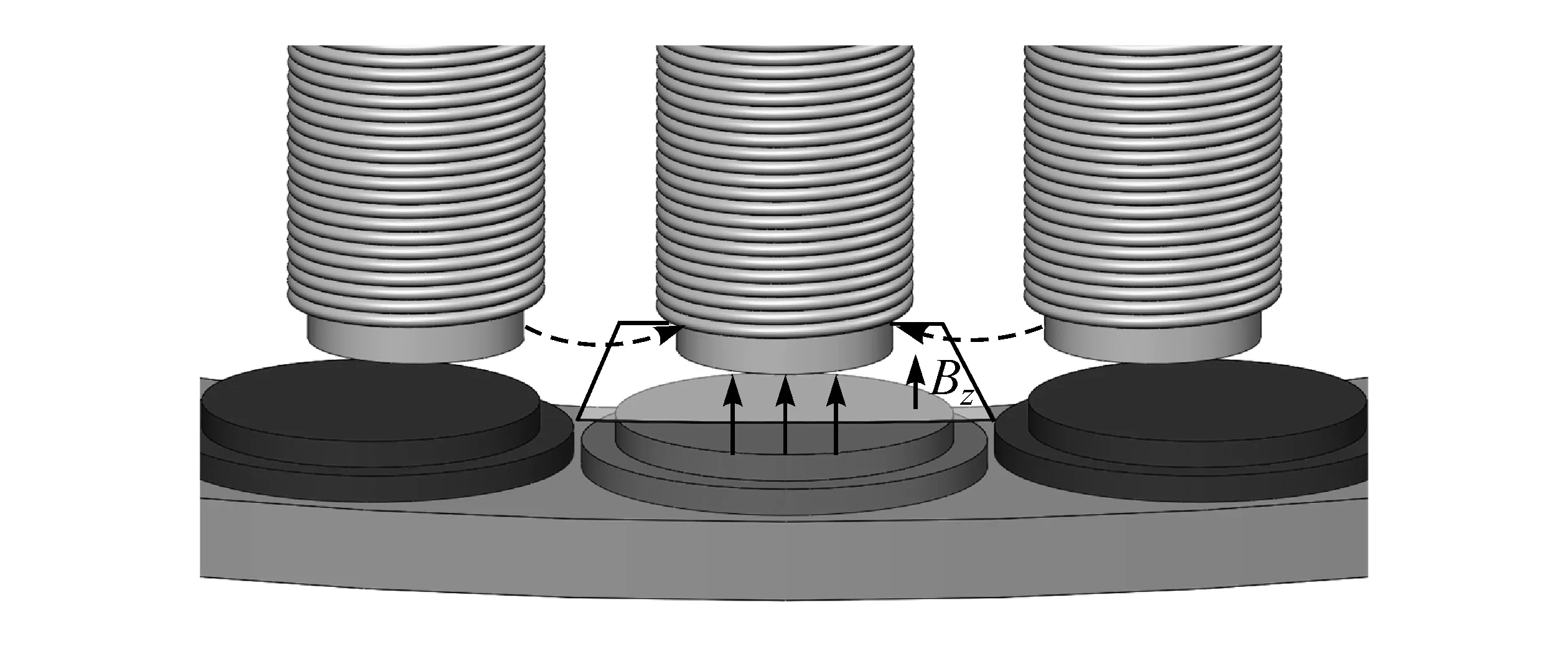
图7 定子齿对应的气隙平面

根据重构后的轴向气隙磁密Bz，可获得轴向磁通量Φz：

A相的总磁链ψa可由下式计算：

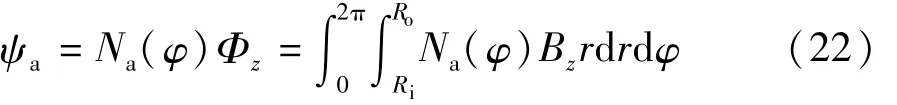
式中Na（φ）为A相绕组函数。样机的A相绕组函数如图8所示，绕组匝数N的取值见表1。

A相的反电动势Vemfa可由下式计算：

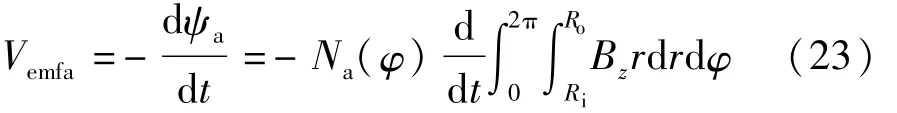
同理，B相和C相的磁链和反电动势可通过移相获得。

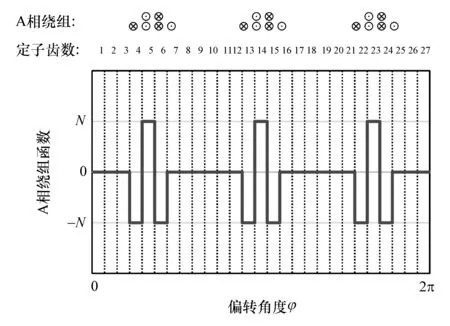
图8 A相绕组函数

3 模型验证与结果讨论

利用ANSYSMaxwell搭建轴向磁通轮毂电机的单元电机三维有限元模型，如图9所示。其中，转子旋转位置数Nq和单位电周期内时间点选取数Ni均为30，即转子每旋转1°机械角度，对气隙磁密进行一次存储。设气隙平面径向层数M为30层，切向段数N为240段，采用IDLE完成定转子基础函数组的提取。采用MATLAB完成三维磁场重构法程序设计。磁场重构后气隙磁密的准确性决定了轮毂电机电磁性能的准确性，采用动态有限元法对气隙磁密的计算结果进行验证，设置单位时间步长为0.15 ms。为了方便比较，选取层数m为1层、6层、11层和16层时的重构气隙磁密与动态有限元计算结果进行对比，如图10所示。由于磁场重构法基于电机的实际结构尺寸、材料和电气参数进行建模，能够反映出较为复杂的定子齿形状和永磁体斜极对气隙磁密所造成的影响。同时，由图10可知，转子旋转位置数Nq和单位电周期内时间点选取数Ni的取值较为合理，除个别点的气隙磁密稍有差异外，整体趋势与瞬态有限元计算结果所得非常接近。

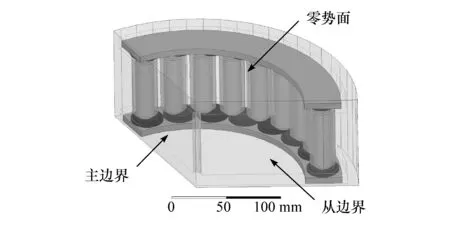
图9 单元电机有限元模型

图11 和图12分别为单侧转子轴向电磁力和电磁转矩的结果对比图。采用磁场重构法获得的单侧转子轴向电磁力平均值为2 313 N，与有限元计算值2 344 N相比，误差约为1.3%。另一侧转子受到大小相等、方向相反的轴向电磁力。采用磁场重构法获得的电磁转矩平均值为19 N·m，与有限元结果19.6 N·m相比，误差约为 3%，转矩波动为1.4 N·m，与有限元结果1.9 N·m相比，误差约为26%。值得注意的是，本文中研究所用的轮毂电机采用了永磁体斜极、定子斜槽和分数槽集中绕组等齿槽转矩削弱技术，齿槽转矩波动频率高且幅值小，无论通过磁场重构法或是有限元法都很难获得准确的齿槽转矩波形。

图10 不同层数处磁场重构法与有限元法各向气隙磁密计算值对比图

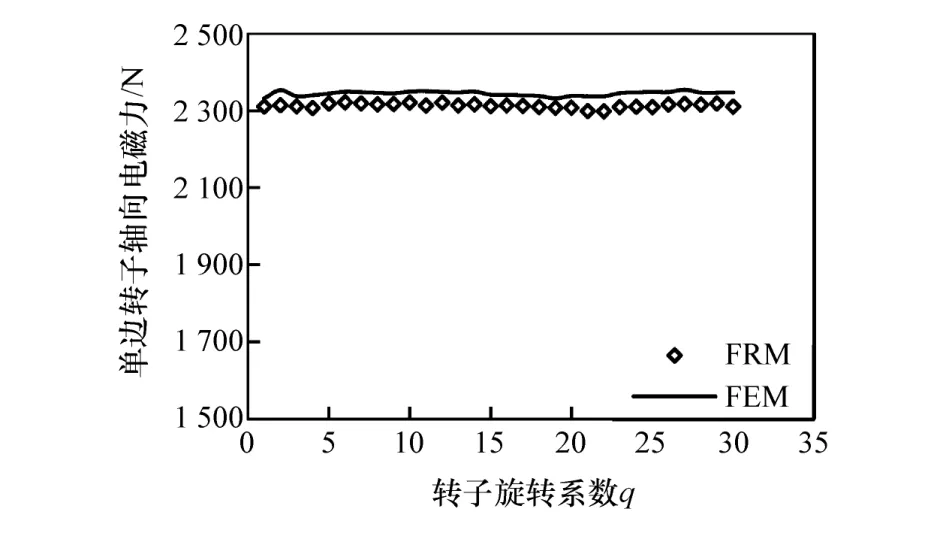
图11 单边转子轴向电磁力结果对比

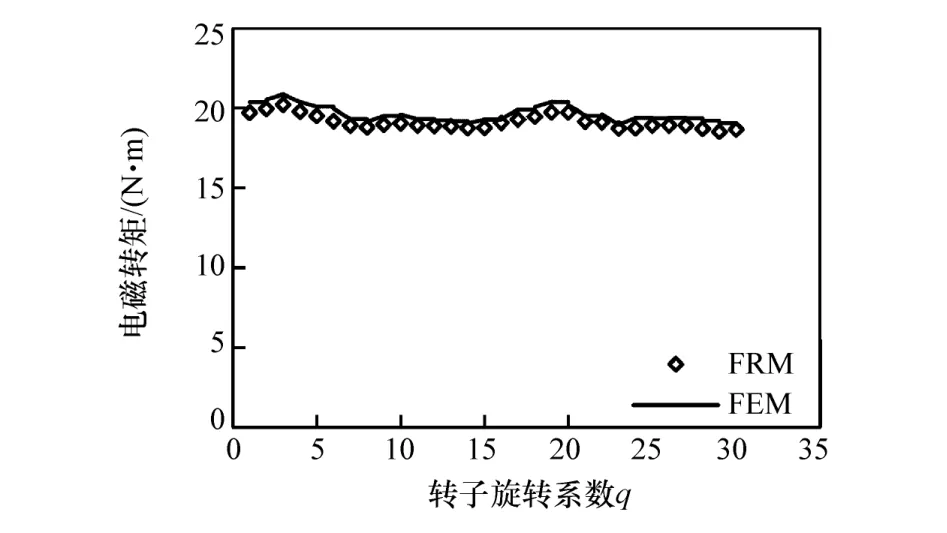
图12 电磁转矩结果对比

图13 和图14分别为A相磁链和反电动势计算值对比图。对图14（a）中A相反电动势波形进行快速傅里叶变换，得到各次谐波幅值图如图14（b）所示。各次谐波幅值与瞬态有限元计算结果基本相等，反电动势基波幅值为53 V，主要谐波为三次谐波，幅值为7 V，总谐波畸变率为16%。

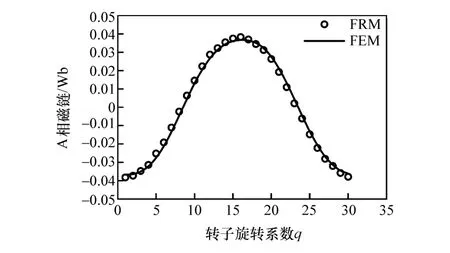
图13 A相磁链结果对比

三维磁场重构法与三维瞬态有限元法网格数量与计算时间对比如表2所示。三维磁场重构法的计算时间显著快于有限元法，其中计算时间并未包含模型的准备时间。三维磁场重构法计算的单元数量相当于一个气隙平面的网格数，显著少于三维瞬态有限元法的网格数，而且三维磁场重构法计算每个时间步长只须在静态有限元结果的基础上线性叠加，而三维瞬态有限元法每个时间步长都须重复一次完整的有限元计算，这是三维磁场重构法速度大幅提升的重要原因。

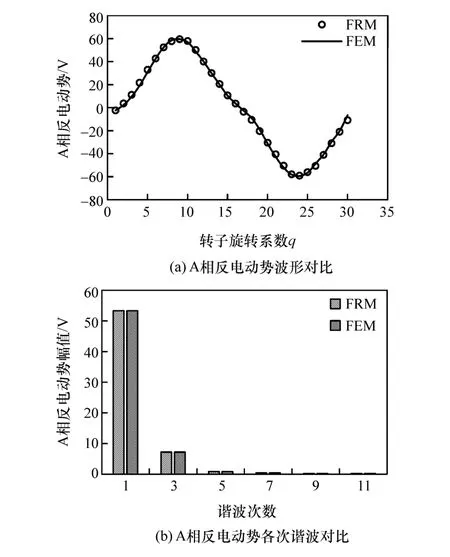
图14 A相反电动势结果对比

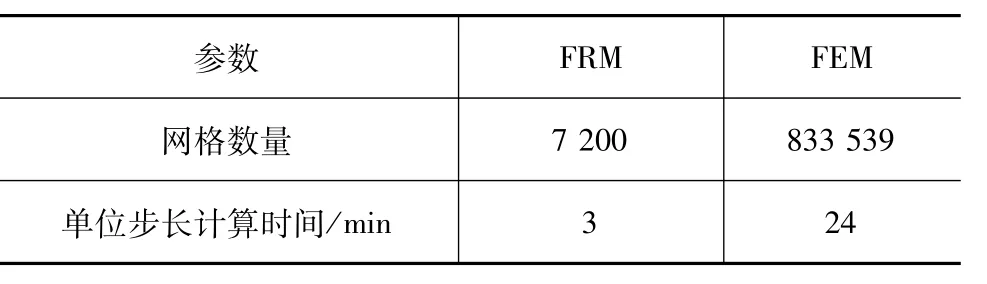
表2 计算时间对比

4 结论

（1）本文中提出了一种适用于定子无磁轭模块化轴向磁通轮毂电机的三维磁场重构法，结合麦克斯韦应力张量法和磁链计算法得到了给定励磁电流和初始位置角下轮毂电机的电磁特性。

（2）与三维瞬态有限元法的计算结果相比，三维磁场重构法能准确计算电磁特性的同时，显著减少了计算时间，能准确高效地预测轮毂电机的电磁特性。