基于遗传算法的机液传动系统参数匹配研究*

朱 镇，蔡英凤，陈 龙，夏长高，施德华

（1.江苏大学汽车工程研究院，镇江 212013； 2.江苏大学汽车与交通工程学院，镇江 212013）

前言

液压传动可柔性地实现减速增矩，多用于车辆的起步工况；液压机械传动具有高效无级调速的特性，多用于车辆的作业工况；机械传动具有较高的传动效率，多用于车辆的转场工况。机液复合传动是一种高功率密度、高效率和连续性的传动方式，综合了液压传动无级调速与机械传动高效变速的优点，可保证车辆的动力性、燃油经济性和通过性，因而对传动系统参数匹配更具研究价值［1-2］。本文中以一款扫地车的机液复合多功能变速器为研究对象，以动力性和燃油经济性为设计目标，根据多目标优化算法确定其主要参数，研究其在不同作业环境下的工作模式。由于路面工况较为复杂，车辆作业时会遇到不同程度的斜坡，因此该类型车辆除一般性能外，还要求具备良好的坡度通过性。

魏超等［3］分析了一款等差式液压机械无级传动装置的传动比特性，揭示了传动比跟踪系统对发动机转速的调节规律，为传动系统参数选择与匹配提供了理论依据。张海军等［4］将中间轴式机械有级变速器和静液压无级变速器并联，基于速度连续和效率最高的原则，确定了传动系统的参数。张明柱等［5］研究了装有液压机械无级变速器的1302R拖拉机的传动特性，根据效率最大的目标函数和约束条件，提出了无级变速拖拉机生产率-经济性综合评价指标和变速规律。Morteza等［6］针对所建立的功率分流混合动力车辆模型，采用基于多输入模糊控制优化的能量管理方法进行研究。Emmanuel等［7］对一种功率分流式混合动力车辆进行全局优化和基于离散动态规划的最优能量管理研究，并利用遗传算法对系统参数进行优化。

1 多功能动力传动装置设计方案

1.1 设计要求

工程车辆的复合传动系统应满足以下条件［8］：

（1）作业和转场工况自由切换，并可互锁；

（2）作业工况时，低速稳定性好，作业动力充足，转场工况时，高速运行，节省时间；

（3）为防止负载过大，在大功率起步或输出状态下增加液压起步挡；

（4）作业工况有较大的动力输出，转场工况发动机动力主要用于提高车速。

1.2 结构方案

机液复合传动装置结构如图1所示。该传动装置以液压传动实现启动和倒退，最大速度不超过5 km／h；以液压机械传动满足作业工况，速度约为5 km／h；以机械传动满足转场工况，速度约为25 km／h。必要时，可增加一个机械挡位，提高转场速度。车辆在作业时，常采用液压传动模式或液压机械传动模式，动力输出轴输出动力驱动清扫机构；在转场作业时，常采用机械传动模式，无动力从动力输出轴输出［9］。

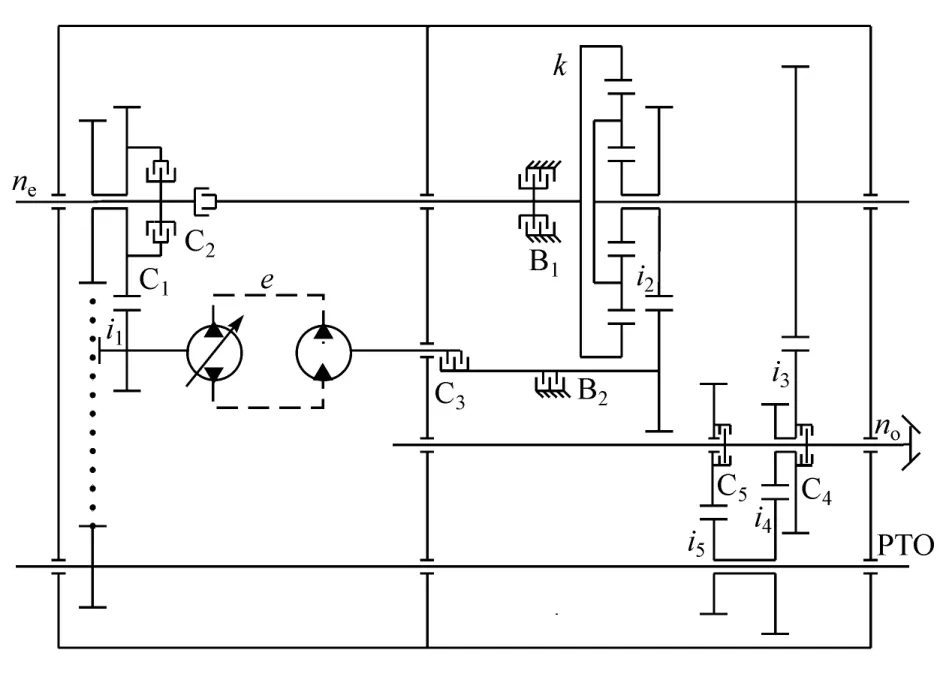
图1 机液复合传动装置结构

各挡位变速传动装置元件状态如表1所示。

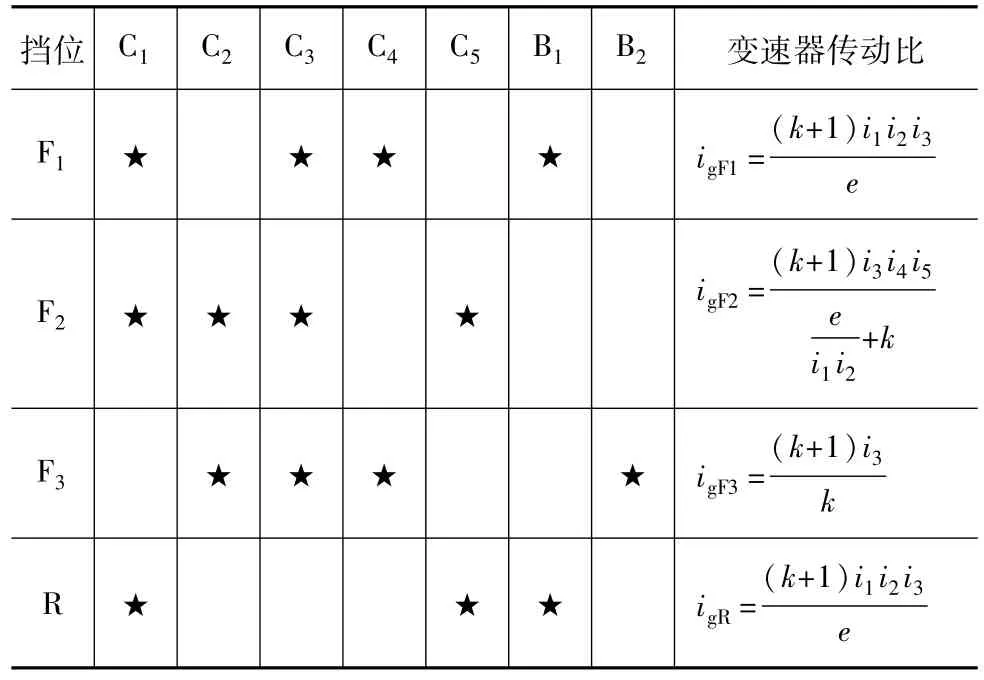
表1 变速传动装置元件状态

传动比为

式中：ne为发动机转速，r／min，nemax＝2300 r／min；rq为轮胎滚动半径，本文中取自由半径为滚动半径，rq＝0.400 m；ua为车速，km／h；iz为主传动比，iz＝22.4。当发动机以额定转速运行时，25 km／h对应的传动比约为0.62。

1.3 动力学分析

车辆行驶方程式［10］为

（1）驱动力Ft

式中：Ft为驱动力，N；Te为发动机转矩，N·m；ηT为系统机械效率。

（2）滚动阻力Ff

式中：Ff为滚动阻力，N；G为车辆重力，N，本文取G＝58 800 N；f为滚动阻力系数，本文取 f＝0.10；α为道路坡度角，（°）。

（3）坡度阻力Fi

式中Fi为坡度阻力，N。

（4）空气阻力Fw

式中：Fw为空气阻力，N；CD为空气阻力系数，本文取 CD＝0.6；A为迎风面积，A＝5 m2。

（5）加速阻力Fj

式中：Fj为加速阻力，N；δ为汽车旋转质量换算系数，δ＞1；g为重力加速度为车辆加速度，m／s2。

根据车辆驱动力 行驶阻力平衡图和爬坡能力的定义，可得

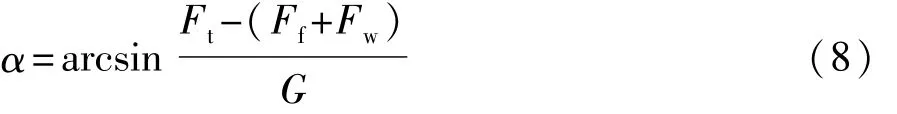
车辆起动时，还要求最大切向牵引力Ftmax不大于附着力即

式中：Ftmax为车辆产生的最大切向牵引力，N；Fφ为附着力，N；φ为附着系数，本文取φ＝0.7。

设计时，仅考虑车辆产生的最大切向牵引力Ftmax大于其满载时在不同坡面克服的阻力的要求，即

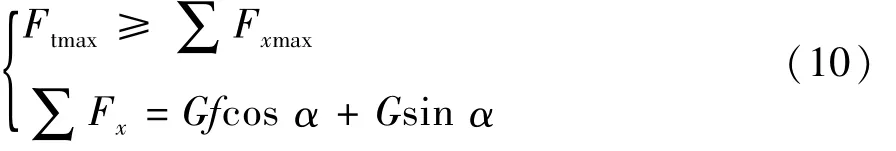
式中：Fxmax为车辆产生的最大切向牵引力，N；∑Fx为满载时在不同坡面克服的阻力，N。

根据式（9）和式（10）可得

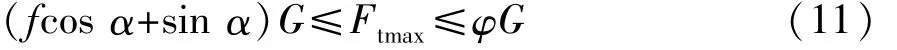
计算得：0.54G≤Ftmax≤0.70G，根据式（3），可知：当215 N·m≤Te≤280 N·m时，都能满足要求，发动机功率范围约为15.8 kW≤Pe≤67.0 kW。

车辆最大牵引力为

式中：FTmax为车辆最大牵引力，可求出地面限制的车辆牵引力为35 280 N。

1.4 发动机选择

发动机是传动系统的动力源，影响着整车性能和许多技术指标，因而在进行传动系统设计时，首先要对发动机进行选型［12-13］。

（1）车辆起步时的最大功率为

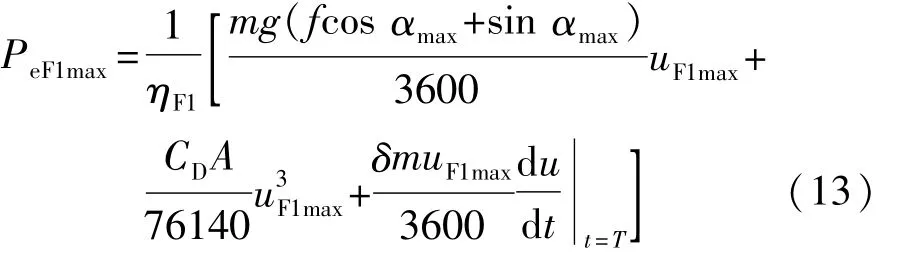
式中：PeF1max为液压挡发动机最大功率，kW；ηF1为液压挡效率；uF1max为液压挡最高车速，km／h；T为某一时间点。

式中：x为拟合系数，本文取x＝0.5；tm为整个起步加速过程所用时间，s；um为起步加速末时刻的车速，m／s；uT为加速过程中 T时刻的车速，m／s。

根据式（13）和式（14），估算可得 PeF1max＝66.2 kW。

车辆作业时的最大功率为

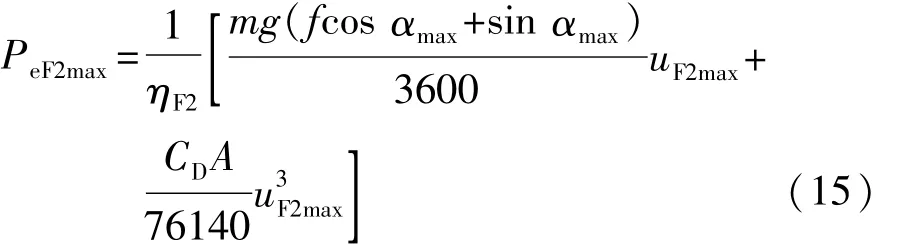
式中：PeF2max为液压机械挡发动机最大功率，kW；ηF2为液压机械挡效率；uF2max为液压机械挡最高车速，km／h。

根据式（15），估算可得：PeF2max＝56.4 kW。

（2）车辆转场作业时的最大功率为

式中：PeF3max为机械挡发动机最大功率，kW；ηF3为机械挡效率；α′为四级公路坡度角，平原微丘区为tanα′＝0.05，山岭重丘区为 tanα′＝0.09，本文取α′＝10°；uF3max为机械挡最高车速，km／h。

根据式（16），估算可得：PeF3max＝110.3 kW。

根据以上各挡位动力性指标的估算结果，发动机额定功率需满足［14］：

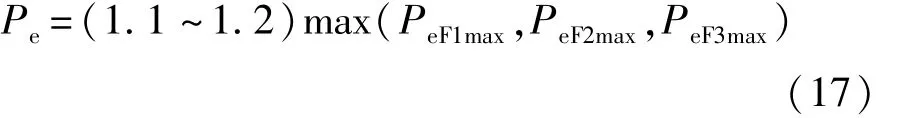
基于此，选择WP4.165E40柴油机作为动力源，其输出功率为121 kW，完全可以满足各种工况的要求，且在作业时可输出一半功率驱动其它机构。

1.5 运动学分析

一般来说，i1的作用是使发动机与变量泵相匹配。i1i2越大，e的调节范围越大；i1i2越小，e的调节精度越高。选择SAUER_DANFOSS055型液压系统，且 e∈［-1，1］，可得：i1＝0.67，i2＝1.5［15-16］。

F1挡和F2挡在中小排量比时，进行无动力中断换挡需满足：

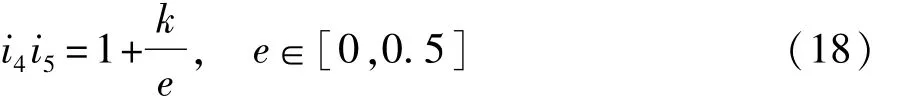
普通齿轮传动比和行星齿轮特性参数应满足：

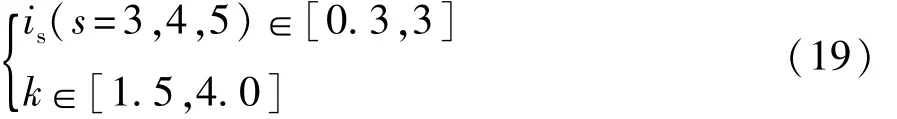
根据式（1），可得车速表达式为

2 基于Pareto最优原理的多目标遗传算法

基于Pareto最优原理多目标遗传算法的基本思想是：在遗传算法的每一代中都可产生大量的可行解，其对应的目标函数值对同一代的各个体进行从优到劣的排序，使排在前面的个体以更高的概率遗传到下一代群体中，经一定代数的循环，即可得到Pareto最优解［17-18］。

2.1 多目标优化问题

多目标优化的目的是寻求解集中的一个或多个满意解，以求解多目标、多约束的优化问题，即寻找一个决策向量，使其满足所有的约束条件和目标函数，这些目标函数是对性能指标的数学描述，常相互冲突。

多目标优化的具体步骤为：鉴别非劣解集，输入偏好信息，选择最佳妥协解。可表述为［19］

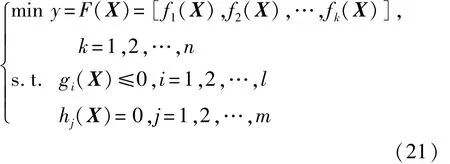
式中：X＝（x1，x2，…，xn）T为决策向量；Y＝（y1，y2，…，yn）T为目标向量；目标函数F（X）表示n个映射函数 f：X→Y；fk（X）（1≤k≤n）为各子目标向量函数；n为子目标的数量；gi（X）为目标函数满足的l个不等式约束条件；hj（X）为目标函数满足的m个等式约束条件。

2.2 Pareto最优原理

一般地，针对多目标优化问题min fk（X），在设计变量可行域内，存在变量X，当且仅当不存在其它变量X*，在不违背约束的条件下，至少存在一个k，使得 fk（X*）≤fk（X）成立，则称变量 X*为多目标优化问题的非劣解，即Pareto最优解。多目标优化中Pareto最优解不是唯一的，有很多个构成Pareto最优解集。Pareto解集是自变量的集合，每一个解集的目标函数就构成了Pareto前沿［20-21］。

双目标优化问题的Pareto前沿示意如图2所示。以两个目标函数分别为横轴和纵轴，确定可行解集。以点A为原点建立局部坐标系，若在该坐标系的第三象限和两个负半轴无其它可行解，则认为点A对应的可行解为双目标优化问题的Pareto最优解。因此，点A和点B对应的可行解都为Pareto最优解，点A偏重于obj2，点B偏重于obj1，点C和点D对应的可行解为劣解。用线将所有Pareto最优解连接起来就得到Pareto前沿。

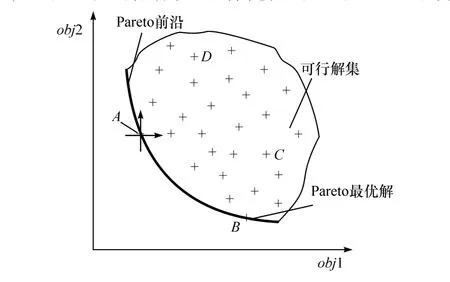
图2 双目标优化问题的Pareto前沿示意图

2.3 遗传算法

遗传算法是一种借鉴生物界适者生存、优胜劣汰演化而来的全局优化自适应概率搜索算法，在解决多目标优化问题时非常有效，其流程如图3所示［22］。

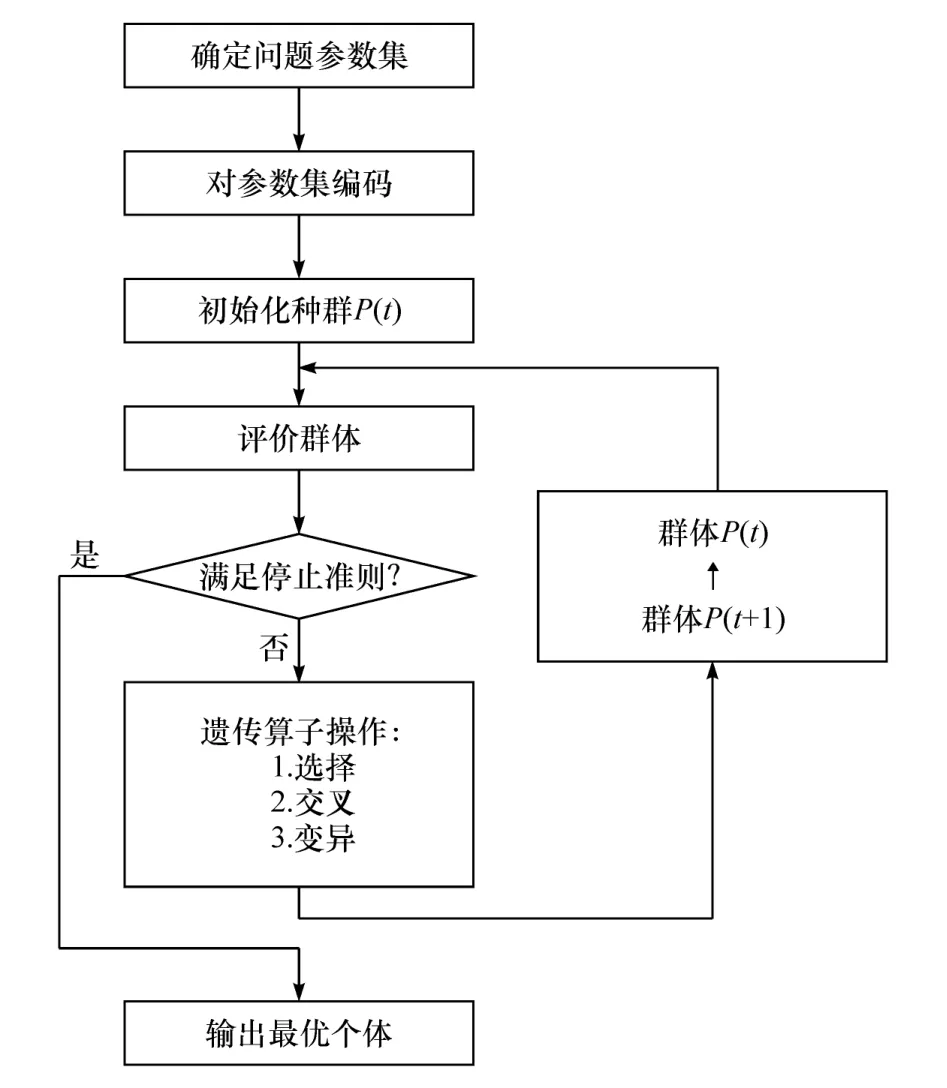
图3 遗传算法流程图

3 机液复合传动系统参数优化

在整车参数、发动机参数和主传动比确定的前提下，变速装置传动参数对车辆的动力性和燃油经济性影响很大，以液压机械挡位为研究切入点，分别以坡度角和燃油消耗率为动力性和经济性评价指标，打破了传统的以动力性为约束条件，以经济性作为目标函数的单目标优化方法的局限性。

3.1 设计变量

在参数优化过程中，使用一组设计参数来表达设计方案，将这些动态变化的设计参数称为设计变量，将设计变量的全体称为设计变量向量。设计变量的选取应遵循以下原则［23］：

（1）设计变量相互独立；

（2）选取对目标函数影响大的变量作为设计变量；

（3）选取有实际意义的无因次量作为设计变量，便于计算；

（4）在满足设计问题的前提下，充分分析各设计变量的主次，减少设计变量的数目，使问题得到简化。

针对本文中的研究对象，选定的优化模型设计变量为

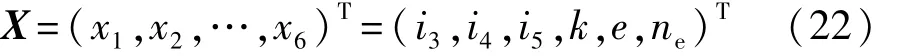
3.2 优化目标

优化设计的目的是对满足约束条件的设计方案进行比较并寻优，而目标函数就作为筛选优化设计方案的评价标准。车辆的动力性和燃油经济性既相互联系又相互矛盾，采用单目标优化法难以解决该类问题。本文中以整车动力性和燃油经济性作为双目标函数，选用最大爬坡度作为动力性优化目标函数，选用燃油消耗率作为经济性优化目标函数［24-25］，即

式中：F（X）为目标函数；G（X）为爬坡度函数；E（X）为燃油消耗率函数。

3.3 约束条件

传动系参数设计时，必须使车辆具有足够的动力性和良好的经济性。同时，在机液复合传动系统设计时，必须使设计变量满足一定的条件。液压机械挡约束条件主要满足式（18）、式（19）和式（24）［26］，即

4 仿真模型

基于modeFRONTIER的传动装置优化模型如图4所示。图中，aF2为液压机械挡爬坡度，geF2为液压机械挡燃油消耗率，vF1，vF2和vF3分别为液压挡、液压机械挡和机械挡速度。

图5给出了模型运行后，经后处理得到的历史图。由图可知：随着优化迭代步数的增加，爬坡度和燃油消耗率两个目标值都呈减小的趋势，并最终在一个小范围内收敛。

正常分位数图检测数据序列的概率分布特性，如图6所示。

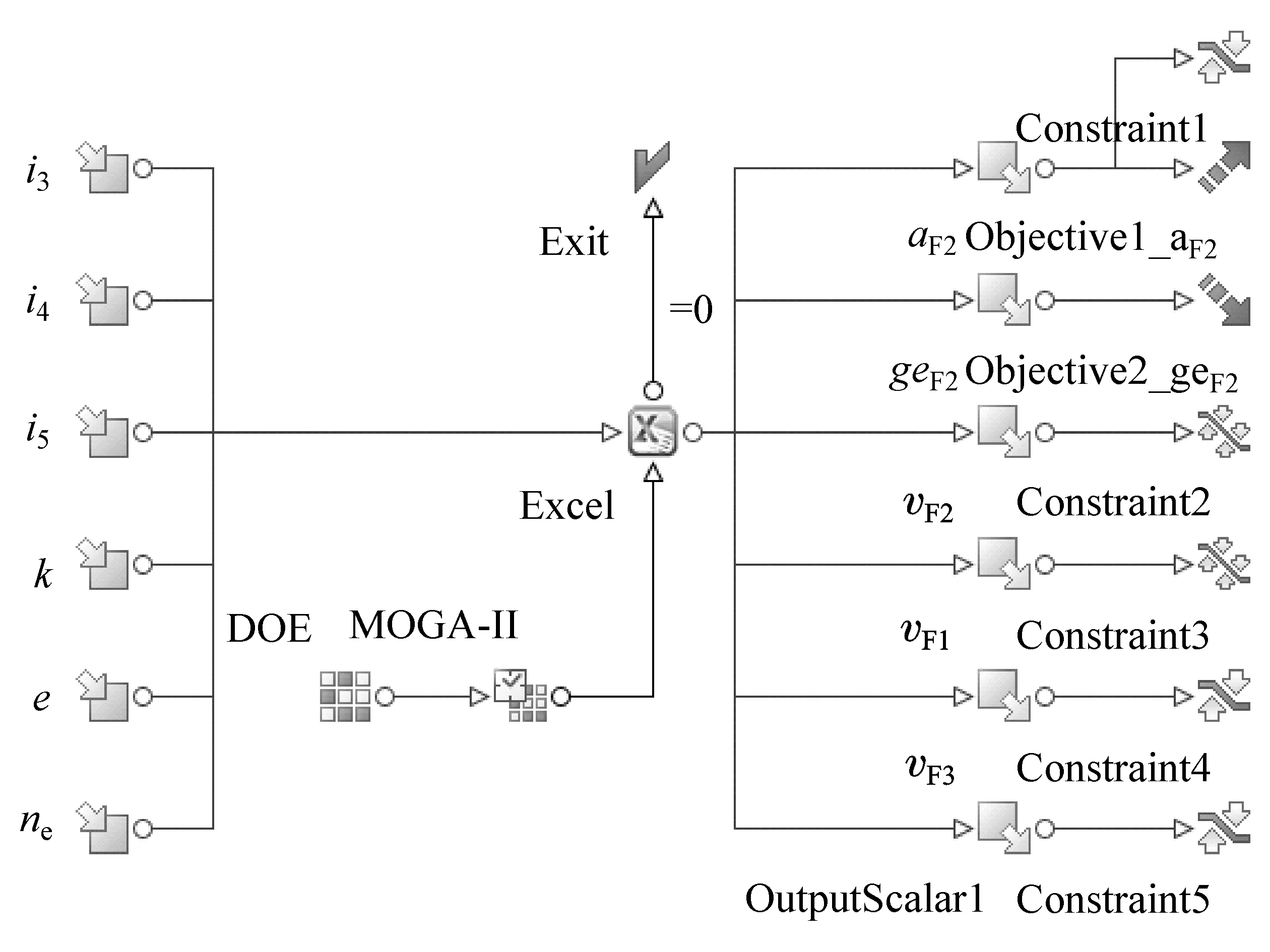
图4 基于modeFRONTIER的传动装置优化模型

可根据软件自带的分析功能得到相关参数：爬坡度平均值为27.26°，95%置信区间为［26.36°，28.16°］。燃油消耗率平均值为208.88 g／（kW·h），95%置信区间为［208.62，209.13］g／（kW·h）。Pareto最优解设计变量为 X＝（0.5，2.0，3.0，2.5，0.5，1300）T，此时可得：Fmin（X）＝（27.93，206.76）。

根据以上优化结果，绘制出如图7所示的调速特性曲线。结果表明：根据优化结果得到的设计变量能够较好地满足传动系统的设计要求［27］。

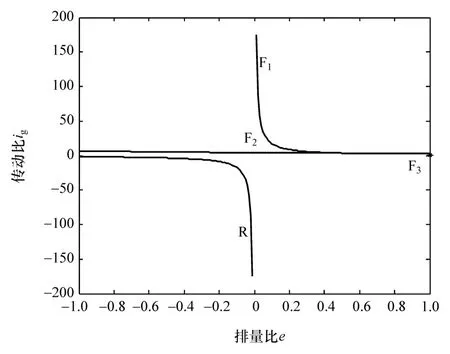
图7 无级调速特性曲线

5 结论

对一款多功能机液复合传动装置进行基于能量管理的多目标参数优化，探讨多模式多工况下传动系统的自适应匹配关系，探究约束条件下满足传动系统目标函数的优化解集。建立基于modeFRONTIER的传动系统目标优化模型，分别以爬坡度和燃油消耗率为动力性和经济性目标函数，使用实验设计与优化算法相结合的方法对多目标遗传算法进行全局搜索寻优。结果表明：爬坡度和燃油消耗率此消彼长，可根据实际要求选取优化解。随着优化迭代步数的增加，爬坡度和燃油消耗率两个目标值都将在一个小范围内收敛，且Pareto最优解的设计变量很好地满足了传动系统的匹配要求。