基于解释结构模型和模糊分析的黄淮海平原区土地利用结构优化——以河北省曲周县为例

史云扬 郝晋珉 陈 红

(中国农业大学 土地科学与技术学院/国土资源部农用地质量与监控重点实验室，北京 100193)

土地是人类一切生产和生活活动的源泉和依托，随着生产力的发展，作为自然物的土地逐渐由生存和发展最基本的生态环境要素转化为人类的劳动对象和劳动资料，人们对于土地利用方式和利用目标的不同会产生不同的土地利用结构[1]。土地利用结构是国民生产结构在土地上的具体安排，通过对区域土地利用结构的协调和优化，可以在不增加物质投入的基础上，产生系统的结构效益，对于区域经济、社会等多方面的高效发展具有重要的意义[2]。

在国内外研究中，不同学者根据研究目标的不同，所采取的研究方式和结果均存在着差异，李鑫等[3]将工科和数学领域中的不确定方法引入土地利用结构优化中，以江苏省扬州市为例，以多目标遗传算法为基础，在多次重复循环下测算出不确定因素在80%可能性发生范围时扬州市土地利用优化结构的弹性区间；黄迎春等[4]将北京和东京市的土地利用状况进行详细对比，对 2020和2030 年的具体目标定量，集成多目标优化模型和元胞自动机-马尔可夫(CA-Markov)模型对北京市土地利用数量结构和空间布局进行了优化；胡振琪等[5]根据矿区土地生态环境脆弱和针对复垦后土地优化结构配置不合理的问题，运用生态足迹法和多目标线性规划法以及景观多样性指数，利用SPSS软件进行择优选取出了符合矿区生态、经济和社会目标的复垦土地利用结构；Habber[6]建立了土地利用分异战略(DLU)，进行土地利用分类，划分区域自然单位(RNU)，通过敏感度和空间关系分析，从生态视角反映土地利用结构，以每个RNU中不同区域对环境影响的敏感性和范围为依据对现状结构进行优化。

对学者们研究所取得成果进行分析发现，目前土地利用结构优化的研究，主要通过建立以目标函数和约束条件为主体的数学模型来实现[1]，但大多数学模型只进行定量分析，对土地利用系统多目标协同、区域系统优化目标体系缺乏深入的研究，且所采取的定量方法多以资本价值量进行核算，难以体现出区域系统的异质性。解释结构模型是刻画大规模复杂系统组成要素间关联特征的一种有效方法[9]，通过构建多级递阶系统结构，可以降低土地利用结构优化目标系统的高熵现象，形成具有层级关系的耦合和协同目标系统。而模糊分析方法可以根据模糊数学的隶属度理论把定性评价转化为定量评价，其与多目标优化模型结合可以对受到多种因素制约的事物或对象做出一个总体的评价，具有结果清晰，系统性强的特点，能较好地解决模糊的、难以量化的问题，适合处理土地利用目标评价量化标准不一致的问题[13]。因此，本研究以区域土地利用系统的角度出发，利用解释结构模型(ISM)分析多目标体系，从黄淮海平原水资源需求压力大的现实条件出发，运用模糊分析方法，将耗水量计入经济-社会-生态的综合效益核算中，以两阶段算法求得土地利用结构优化方案，同时将优化方案与自然演化方案、现状方案进行对比并进行分析，旨在为黄淮海平原区土地合理利用提供新的科学依据，为区域土地利用规划的制定提供借鉴。

1 研究方法

1.1 多目标优化模型

多目标模型是目前土地利用结构优化的趋势，其主要由目标函数和约束条件两部分组成，优化即寻求在给定约束条件下达到最佳目标的途径，目标函数反映系统的功能目标与结构相互依存的关系，约束条件通过待定变量在数量上的表现得以体现。以多目标优化模型为基础框架，嵌入模糊分析和解释结构模型方法，得到多目标帕累托非劣解，最终通过比较分析可以获得最优解。

目标函数：

max(min)f(x)=(f1(x),f2(x),f3(x)…fn(x))T

(1)

约束条件：

(2)

式中：fi(x)=Bx，x=1，2，…,n；x为所求变量向量，B为目标函数的系数矩阵，x= (x1，x2,…,xn)T，Bi=B1，B2,…,Bn，n为变量个数。

1.2 解释结构模型

解释结构模型(Interpretative structural modeling，ISM)是Warfield[7]在1971—1973年为分析复杂系统的结构模型而开发的一种系统分析方法，它可将系统中各要素之间的复杂的和零乱的关系分析成清晰的多级递阶的结构模型，是一种用于分析和揭示复杂关系结构的有效方法。土地利用优化系统中的各目标存在着复杂的相互关系，很难清晰地理清其中心目标和辅助目标以及各目标的隶属层级关系，解释结构模型可以降低土地利用结构优化目标系统的高熵现象，形成具有层级关系的耦合和协同目标系统，也可以通过目标对优化模型进行限制条件的量化，有助于提高优化的系统性和层次性。

ISM的具体实现方法如下[8]：

1)生成连接矩阵。充分了解系统的各个组成要素Si(i= 1,2,∧,n)，并确定各组成要素Si和Sj之间的关系， 把2项关系的有无归纳成连接矩阵A=〔aij〕的形式,设矩阵A的(i,j)元素aij取值如下:当2项关系成立时为1,不成立时为0[9]。

2)生成可达矩阵。求A与单位矩阵I的和A+I,对某一整数n做矩阵(A+I)的幂运算(幂运算是基于布尔代数运算进行的),直至下式成立为止:

M=(A+I)n+1=(A+I)n≠A+I

n=1,2,…

(3)

矩阵M= (A+I)n称为可达矩阵。

3)生成缩减矩阵。合并可达矩阵M中相同的行和列。

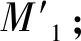
5)生成多级递阶结构模型(图1)。

图1 ISM核心部分简化图Fig.1 Core section simplification of ISM

1.3 模糊分析两阶段算法

在多目标规划过程中常常会出现目标函数性质和量纲不一致的情况，模糊分析方法可以通过制造模糊环境，以目标函数满意度代替原规划目标值，从而以目标函数满意度来寻求多目标规划中的条件极值[10]。通过模糊分析方法中的两阶段算法，可以通过满意度的形式统一各目标的评价标准，并以综合满意度作为最终方案的评价依据。

1.3.1最大(小)算子法

在多目标线性规划中，各目标函数在约束条件下很难同时达到各自的最优解。为此，Zimmermann等[11]针对多目标问题的决策方法，提出了最大(小)算子法，求得目标函数最小满意度的最大值。其实现途径如下[12]：

1)构建目标函数满意度隶属度函数。为了选取合适的初始值,决策者以反理想值向量为参考点,即选取初始值不小于反理想值,进而可定义各个目标值满意度的隶属度函数。首先求出各目标函数在约束条件下的理想值与反理想值，公式如下：

(4)

式中：x为模型变量，Zi(x)为目标函数，Ax≤0是约束条件。

然后以各函数理想值与反理想值构建满意度隶属度函数，设第i个目标函数满意度为ui，则有：

(5)

2)计算最小满意度。最大(小)算子法可以使各目标函数最小满意度达到最大，保证了解的公平性，使得所有函数满意度均在合理的解释区间内，其公式如下：

(6)

式中：k=1,2，…,n

1.3.2两阶段算法

由于在最大(小)算子法中最小满意度的提高一方面可以使得某一目标函数更加接近最优值，另一方面也可能使其他函数值远离最优值，当某一函数的最小满意度设置过大时甚至可能出现整体无解的情况，为此Lee[13]将平均算子法和最大(小)算子法结合，提出两阶段算法，以弥补不足，其实现算法如下：

1)以反理想值作为初始值代入最大(小)算子法中，得到各目标函数的最小满意度以及满意度的最优解x。

2)通过x得到相应目标函数的隶属度函数uk(x0)(0≤k≤1),并令λk=uk(x0),代入如下公式中,求得最优值即两阶段算法求得的解。

(7)

式中：k=1,2,…,n

1.4 基于Markov过程的土地利用转移矩阵预测

Markov过程是一种特殊的随机运动过程。如果随机过程X(t)在时刻(n+ 1)状态的概率只与时刻n的状态有关,而与n以前的状态无关,则称随机过程X(t)为一个Markov链[14]。记条件概率P{X(n+1)=j|X(n)=i}=Pij(n)，Markov过程具有无后效性及齐次性，其与土地利用转移矩阵结合，可以计算出当前自然演化下区域土地利用结构变化情况[15]，将自然演化下的区域土地利用结构情况同经优化后的土地利用结构进行对比分析，可以对优化方案的合理性进行验证。

设土地利用转移概率矩阵为：

(8)

转移矩阵中各元素为相应转移矩阵行列元素之和的比值:

(9)

那么对某一转移时段来说，时段起初所有地类面积向量t和期末的地类面积向量t'关系如下:

t′=t×pij

(10)

对于n个连续时段，存在n+ 1面积向量t1，t2，…，tn+1， 可得:

(11)

那么可以定义:

(12)

P(a,a+n)即为总时段下的土地利用转移矩阵，同时结合土地利用转移现状结构矩阵即可得到目标时段下的土地利用结构。

2 实证研究

2.1 研究区概况

黄淮海平原地理坐标位于32°00′N～40°30′N、113°00′E～121°00′E，包括京、津、冀、鲁、豫、苏、皖 7省 (市),总面积约31万km2，人口和耕地面积约占全国的1/5，是我国重要的农业生产基地。同时，由于长期的农业耕作以及存在着面积巨大的地下水漏斗地貌，黄淮海平原区域生态安全尤其是水资源安全面临着巨大挑战[16]。曲周县地处河北省南部，太行山东麓黑龙港流域上游地区，属暖温带半湿润大陆性气候，多年平均降雨量为556 mm，是黄淮海平原典型农区。截至2012年末，曲周县土地总面积为67 668.09 hm2，其中农用地56 645.24 hm2，占土地总面积的83.71%，建设用地9 635.35 hm2，占土地总面积的14.24%，未利用地1 387.50 hm2，占土地总面积的2.05%，耕地面积比重大，生态用地面积和城镇土地集约化水平有待提高，农村居民点缺乏统一规划，2017年曲周县被住建部提名为国家园林县城，未来曲周县面临产业转型压力，在保障生态功能的基础上拓宽经济发展渠道，因此有必要对曲周县土地利用结构进行优化调整。

2.2 数据来源

本研究主要采用了曲周县2012年土地利用现状数据、2012—2015年土地利用变更数据、2020年土地利用规划指标数据、农业、工业、服务业等相关部门的经济核算数据、各类用地固碳排碳数据以及区域内各地类耗水量数据等6个方面的基础数据。1)曲周县2012年土地利用现状数据、2012—2015年土地利用变更数据来源于曲周县2012—2015年土地利用更变数据表。2)2020年土地利用规划指标数据来源于《曲周县2010—2020年土地利用总体规划调整完善方案》。3)国民经济各部门相关核算数据来源于《2012年曲周县统计年鉴》。4)各类用地排碳数据根据赵荣金等[17]对于中国不同产业空间碳排放研究，固碳数据根据王博等[18]的研究，数据结果如表1。

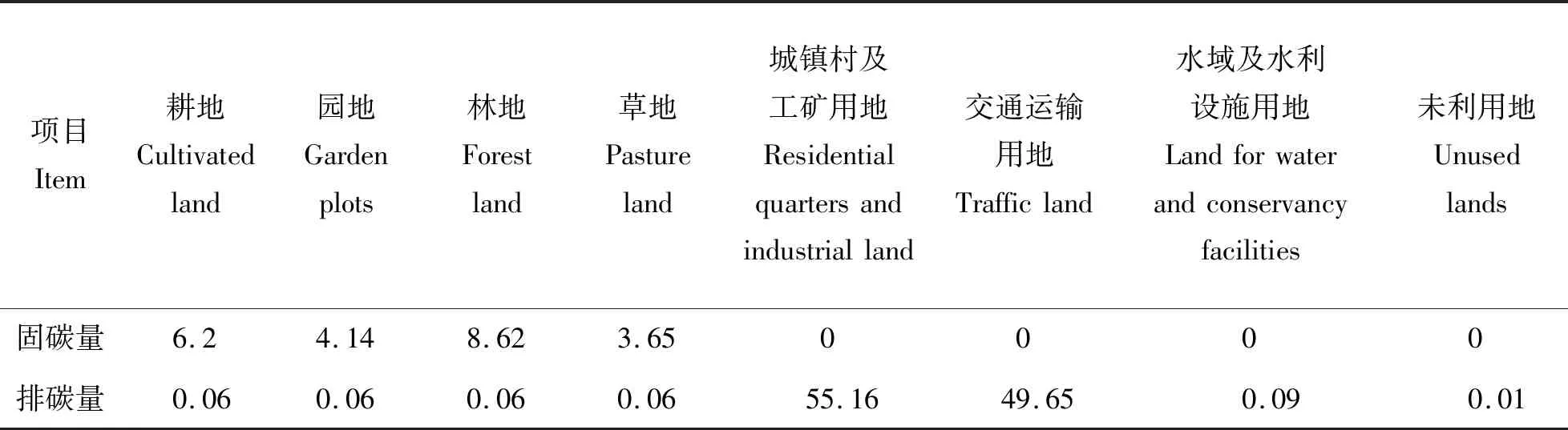
表1 不同地类单位土地面积年均固碳排碳量Table 1 Annual carbon sequestration and emission of different land type in unit area t/hm2

5)各地类耗水量数据来源于雷鸣等[19]对于黄淮海平原地下水资源量的研究，经过单位换算得到黄淮海平原区平均耕地耗水量为5 700 m3/ hm2，园地耗水量为6 331 m3/ hm2，林地耗水量为5 659 m3/ hm2，草地耗水量为5 093 m3/ hm2，城镇村工矿用地和交通用地耗水量为16 600 m3/ hm2，水域及水利设施用地耗水量(蒸发为主)为耗水量为4 938 m3/ hm2，未利用地耗水量为4 939 m3/ hm2。

2.3 变量设置

变量的设置选取是模型构建的关键。本研究考虑下列原则设置决策变量： 1)变量的选择符合《全国土地分类》和土地利用总体规划要求。2)全部变量应覆盖区域所有现存地类，并保持其独立性，不能重叠。3)变量设置应体现获取数据的典型性和便利性特征。综上所述，变量设置如表2。

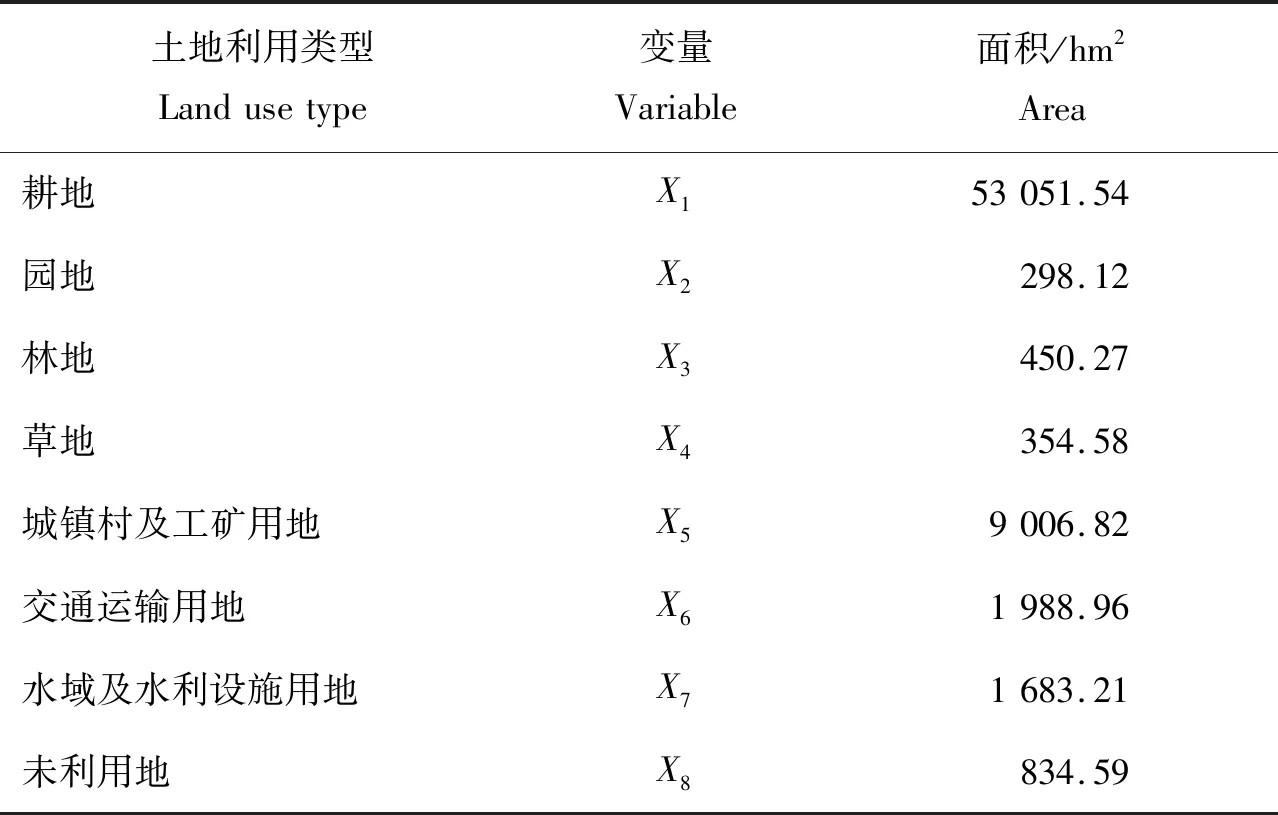
表2 曲周县2012年土地利用结构及模型变量说明Table 2 The land use structure and model variables of Quzhou County in 2012

2.4 区域土地利用结构优化模型构建

2.4.1区域土地利用结构优化目标体系

土地利用结构是国民经济结构落实在土地上的直接或者间接反映，因此土地利用结构的优化目标包含着来自社会、经济和生态等诸多方面的要素协同与融合关系，各优化目标之间往往具有相互影响的关系层次[1]。表3列举出了曲周县土地利用的一般优化目标[20]：

根据ISM的基本原理[7-8, 21]，首先通过专家咨询以及查阅相关资料，对各目标之间的相互关系进行界定，形成目标间的连接矩阵，之后遵循布尔计算以及后续算法，得到区域土地利用结构优化目标的多级递阶系统结构模型，如图2。

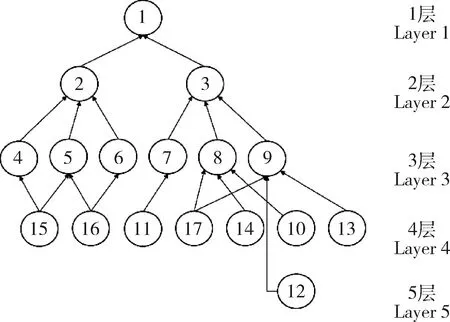
图2 曲周县土地利用优化目标体系结构Fig.2 Land use optimization of the target architecture in Quhou County

可见，曲周县土地利用优化目标体系中总目标为①即促进土地可持续利用，它的实现有赖于第二层子目标②(促进土地利用公平)和③(提高土地利益效益)的改善，而第二层目标的实现又依赖于第三层目标的完成，其他各层次与之类似，由此构建出关系明确，层次清晰的区域土地利用结构优化目标体系。

2.4.2目标函数构建

本研究设定经济、社会、生态效益以及耗水量4个目标函数作为L2层目标③以及L3层目标⑦、⑧和⑨的转化，单位面积各地类效益系数(单位面积土地价值量产出)与面积数的乘积之和共同构成目标函数的核算方程。

1)经济效益目标函数、社会效益目标函数。借鉴李景刚[22-23]对土地可持续规划中资源价值的核算研究，对曲周县相关经济社会数据进行核算可得区域各地类单位面积效益系数，如表4所示。

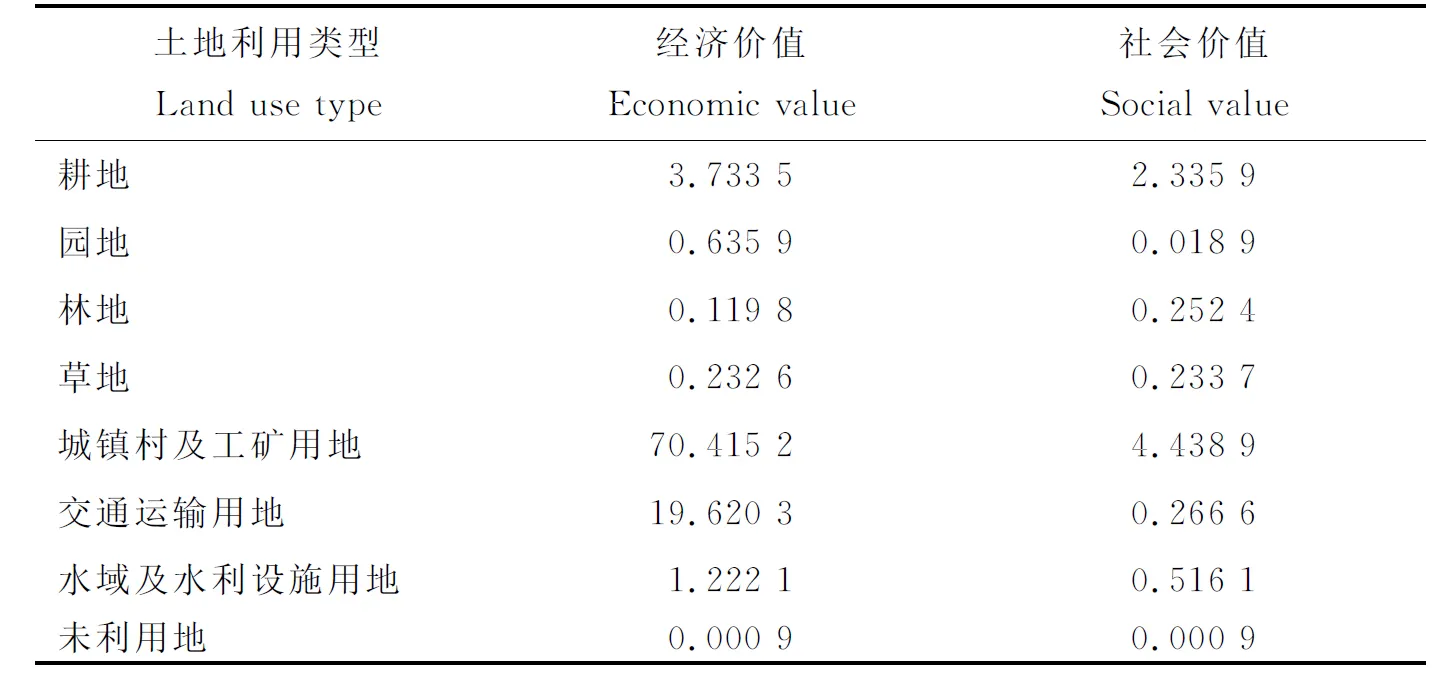
表4 曲周县不同地类单位面积经济、社会效益系数核算Table 4 Different types of unit area of economic and social benefit coefficient calculation in Quzhou County 万元/hm2

2)生态效益目标函数。随着社会生产力的不断发展，生态安全的重要性愈发受到重视。大多数生态功能难以准确计量，参考相关研究，依据“木桶法则”和“最小因子定律”，以无法替代、不能交易、数量稀缺作为测算基础和依据，选择以各地类的气体调节功能为切入点，通过碳平衡方法来体现区域的生态效益水平[18]。各地类的生态效益系数如表5。

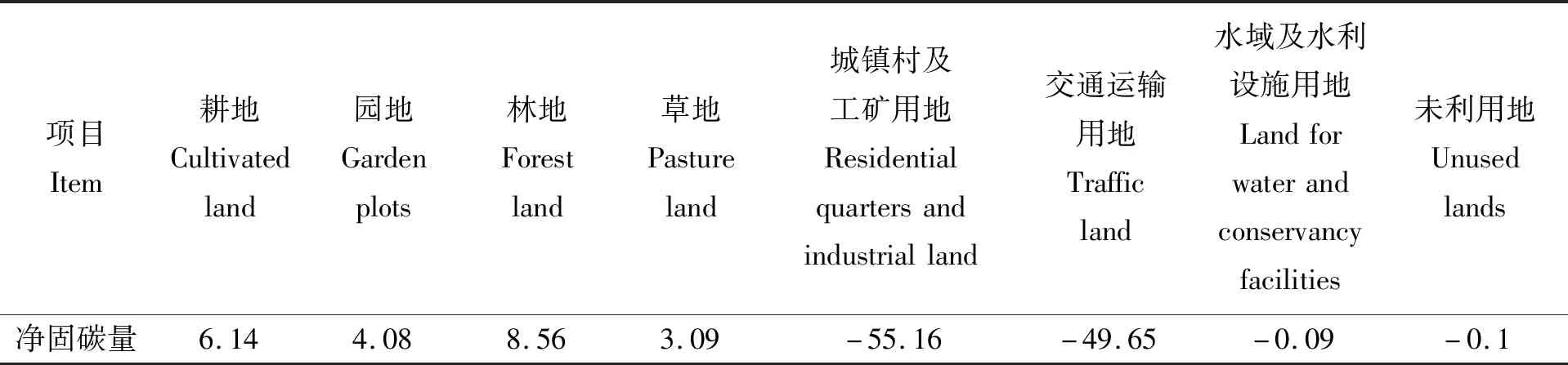
表5 曲周县不同地类单位面积生态效益系数核算Table 5 Different types of unit area of ecological benefit coefficient calculation in Quzhou County t/hm2

3)耗水量目标函数。黄淮海平原是我国重要的粮食生产基地，对于国家战略粮食安全具有不可替代的地位，同时该地区也是世界三大地下水漏斗区，地面沉降严重，水资源承载力面临挑战。曲周县地处黄淮海平原腹地，是传统的农业生产大县，土地利用结构优化中必须注意区域水资源平衡，因此引入耗水量目标函数，以各地类平均耗水量作为核算效益系数。

同时由于各目标函数中统计量单位不同，为了方便效益函数的综合分析，通过SPSS软件运用z-score 法对数据进行标准化得到各效益目标函数如表6。

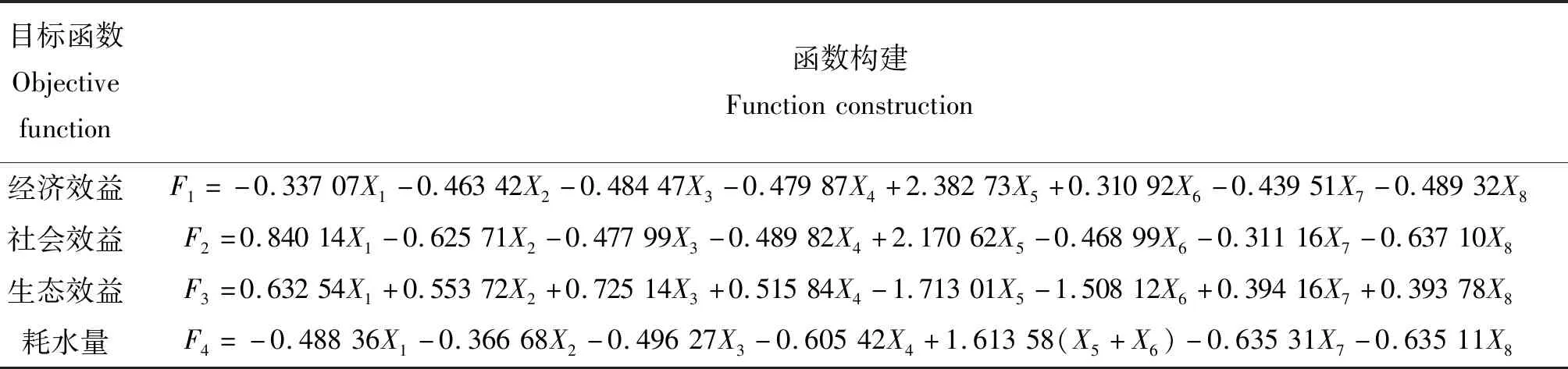
表6 曲周县土地利用目标函数Table 6 The objective function of land use in Quzhou County

2.4.3约束条件设定

1)土地利用公平子目标约束。土地利用公平是土地可持续利用评价的一项重要组成部分，但是由于各种现实原因，土地利用公平难以在核算中进行量化分析。本研究采用但承龙[24]的方法，通过各地类面积符合土地利用远景规划限制来表示土地利用公平即将目标②、④、⑤、⑥和转化为下式约束：

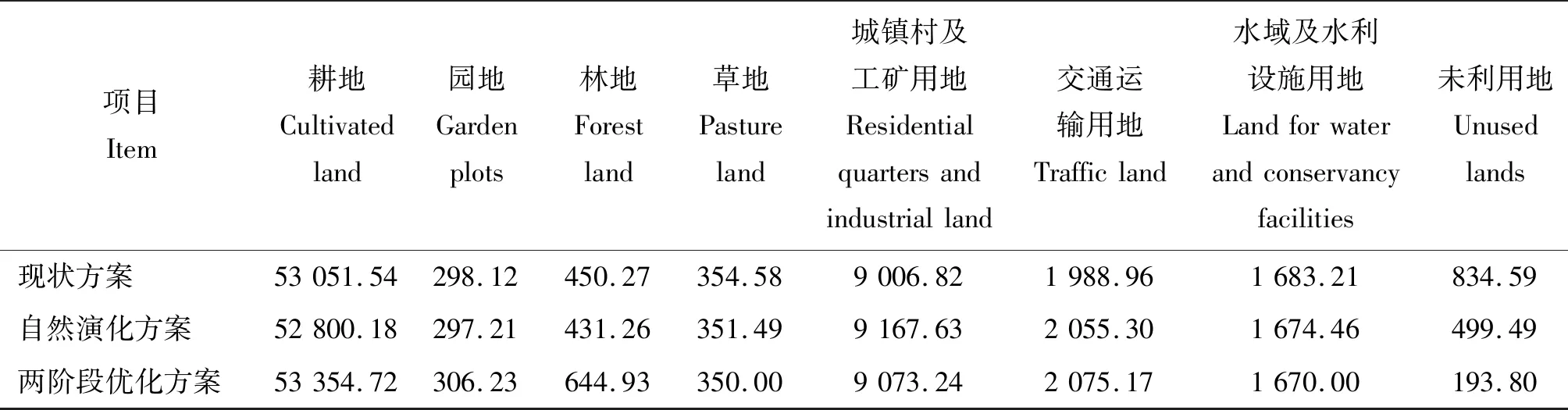
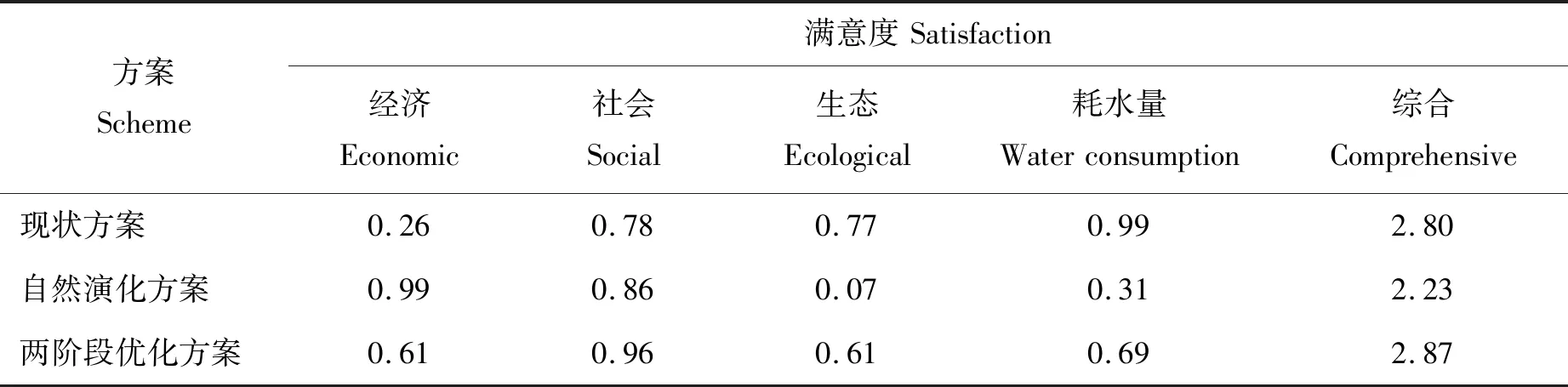
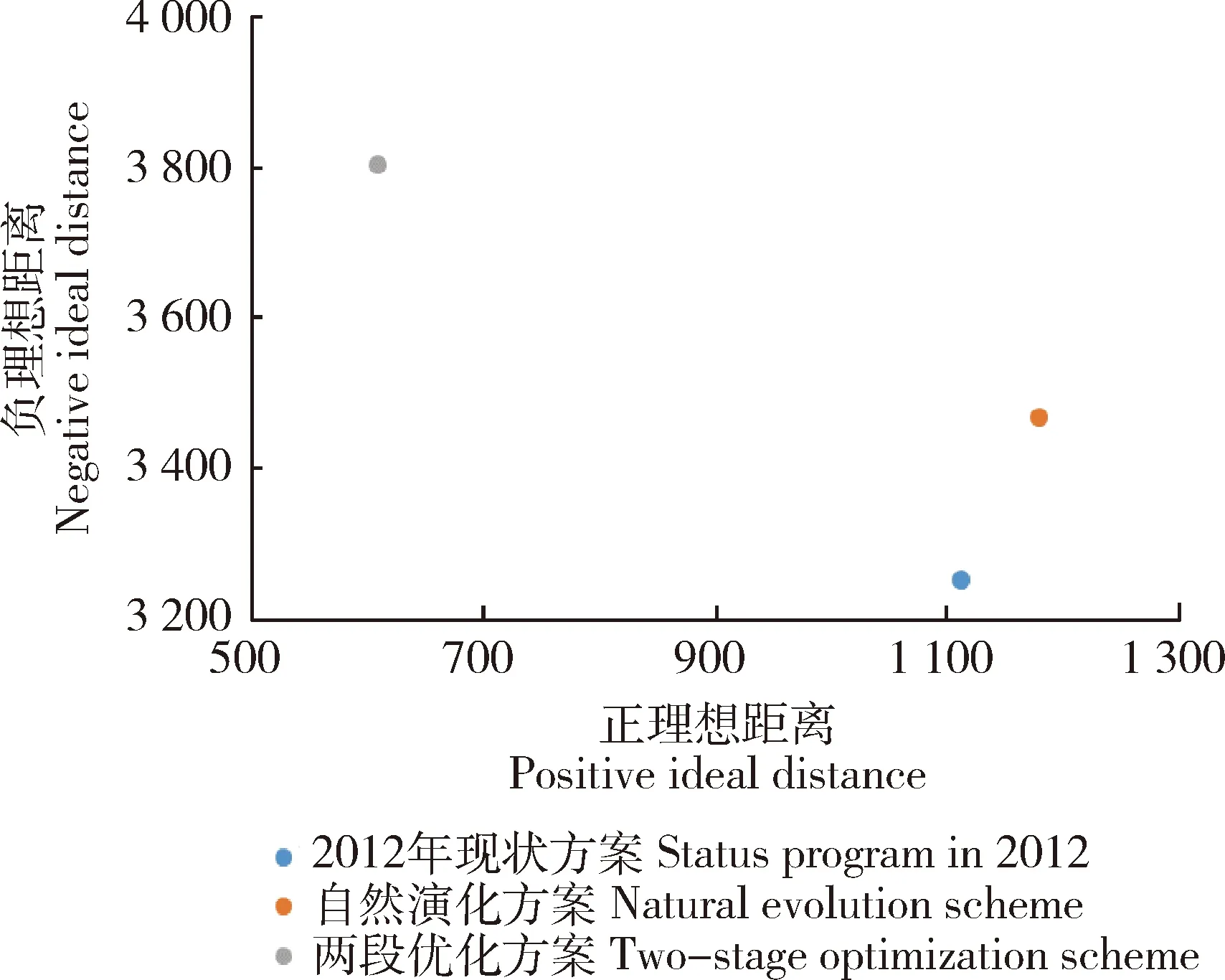
x1≥U,x2≥M,x3≥E,x4≥
T,x5+x6

(13)

式中：U、M、E、T、I和V分别表示《曲周县2010—2020年土地利用调整完善方案》中耕地保有量、园地、林地、牧草地、建设用地总规模的总量指标以及新增建设用地的增量指标。

x建设用地占农用地新增指标<α,x建设用地占耕地新增指标<
β,x整理开发复垦耕地指标>γ

(14)

x5+x6>δ

(15)

(16)

式中：α、β和γ分别表示《曲周县2010—2020年土地利用调整完善方案》中新增建设用地占用耕地规模、新增建设用地占用耕地规模、开发整理复垦补充耕地增量指标，δ表示基期建设用地面积，ε表示基期土地利用率。

x基本农田面积≥ζ

(17)

∑aixi∶∑ajxj∶∑akxk=l1∶l2∶l3

(18)

式中：ζ为基本农田保护目标面积，xi、xj和xk分别为曲周县一、二和三产用地面积，ai、aj和ak分别为一、二和三产用地单位面积社会效益产出，l1∶l2∶l3为产业结构调整目标，根据《曲周县国民经济和社会发展第十三个五年规划纲要》目标及本研究土地利用分类体系，产业机构目标为一产用地面积∶二三产用地面积=3∶17。

(19)

∑wixi

(20)

其中：η为基期生态用地保有率，W为区域供水总量，取值为561.3万m3。

5)其他约束。

非负约束：xi≥0,i=1,2,…,8

(21)

(22)

式中：S为曲周县土地总面积。

至此,图2中所示的土地利用系统优化目标体系,均已量化为多目标系统优化模型的目标函数和约束条件。

2.5 土地利用结构优化方案

基于非线性规划软件Lingo11平台，结合上述目标函数及约束条件模型参数，运行模糊分析两阶段算法程序，进行求解可以得到相应的Pareto最优解，其最小满意度λ0=0.61，模糊折衷指数λ*=0.72， 另外基于Markov链通过土地利用转移矩阵对自然演化方案下2035年曲周县土地利用结构进行预测，它们得到的结果如表7。

表7 曲周县土地利用结构优化方案对比Table 7 Optimization of land use structure comparison in Quzhou County hm2

2.6 土地利用结构优化方案评价

2.6.1土地利用结构变化分析

通过对3种不同情况下土地利用结构进行分析可以得到，耕地、城镇村及工矿用地以及交通运输用地仍是曲周县土地利用结构中占主体地位的3种地类，3种地类面积占土地总面积的90%以上，其中耕地占比最大，平均占比达到78%，说明曲周县农业生产大县的角色定位长期稳定，故耕地数量的保证是区域经济社会发展的重要前提。同基期相比，经两阶段算法优化的土地利用结构中耕地、林地、未利用地的变化最为明显，耕地、林地的占比上升了0.45%和0.28%，未利用地下降了0.94%，耕地、林地的增加来源也主要来自于未利用地，而自然演化方案下的土地利用结构耕地、林地面积均有所下降，说明优化后的土地利用结构对于生态用地面积的增加以及土地利用程度的提高具有明显的贡献。另外在建设用地方面，优化方案较现状占总量的比重增加了0.23%， 但较自然演化方案下减少了0.13%，优化方案满足了曲周县经济发展规划下关于产业结构的目标，说明曲周县存在建设用地扩增速率过快的问题，优化方案对于抑制不合理的用地需求也起到了一定的作用。其余地类比重变化均在0.1%以内，结构相对稳定(图3)。

图3 曲周县不同方案土地利用结构对比图Fig.3 Comparison of different schemes of land use structure in Quzhou

2.6.2模糊决策满意度分析

运用模糊分析方法，将3种不同情况下土地利用结构的相关数值代入满意度算法[25-26]中，可以分别得到其经济、社会、生态、耗水量以及综合的满意度值(表8)。

研究发现，经过两阶段算法优化后的土地利用结构其综合满意度明显高于基期水平，经济、社会满意度较之均有大幅度的提高，但生态、耗水量方面却下降了，究其原因，是因为在优化模型中生态效益和耗水量方面效益系数较低的城镇村及工矿用地和交通用地面积较基期显著增加，在满足了经济、社会效益提高的同时一定程度上损害了生态和耗水量的效益；另外，未利用地的开发也是导致效益下降的原因之一，未利用地对于生态、耗水量效益的负相关性较弱，而未利用地被开发为建设用地这类负相关性较强的地类就会降低生态方面的效益，但是县域社会生产力的发展需要保证足够的建设用地数量，健康的城镇发展水平是要在多种限制条件下达到综合效益最优的平衡点，所以综上，两阶段算法优化后的土地利用结构是优于现状结构的。同时，自然演化方案下(2035年)其综合满意度最低，虽然其经济效益、社会效益尤其是经济效益有了显著的提高，但是生态、耗水量效益损失更为严重，从侧面也反映出了当前曲周县大力追求经济社会效益，对于生态等考量不足的发展观，这种发展观反而会阻碍曲周县土地利用的综合水平，土地利用结构优化的现实需求十分迫切。

表8 曲周县土地利用结构不同方案满意度对比Table 8 Different land use structure scheme comparison satisfaction in Quzhou

2.6.3土地利用结构合理度分析

土地利用结构合理度评价是土地利用结构调整与优化的基础，也是土地利用总体规划的核心内容。本研究采用TOPSIS法中关于土地利用结构合理度Ri的计算方法[27]，通过计算样本点同理想点的相对距离进而得到合理度Ri，相对距离通过正理想距离和负理想距离进行表征，正理想距离表示样本点靠近理想点的直线距离，其距离越小表示越靠近理想点，合理程度越高；负理想距离表示样本点远离理想点的直线距离，其距离越大表示越远离理想点，合理程度越低。具体的计算公式如下：

(23)

根据相关算法，可以得到三种不同情况下土地利用结构合理度分别为R2012现状=11.09、R自然演化方案=11.77、R两阶段算法优化=6.04，对比可以看出经过两阶段算法优化后的土地利用结构其合理性最强，另外在计算到非理想点的相对距离后，同样两阶段算法的结果距离非理想点最远，土地利用合理程度最高。(图4)

图4 曲周县不同方案土地利用结构理想距离图Fig.4 Ideal distances of different schemes of land use structure in Quzhou

3 结论与讨论

3.1 结 论

本研究基于多目标规划模型，将目标函数和约束条件通过解释结构模型(ISM)同规划目标相衔接，并利用模糊分析法中的两阶段算法对土地利用结构进行优化，经过实证分析和实际经验，通过对比曲周县2012年基期、自然发展2035年以及两阶段算法优化结构在合理性等方面的结果，证明该研究方法可以有效地优化现有的土地利用结构，可以达到土地利用系统内不增加投入情况下的结构效益，主要的研究结论如下：

1)以多目标优化模型为基础框架，嵌入解释结构模型和模糊分析算法进行区域土地利用结构优化的方法，可以对土地利用优化目标体系进行系统的层次性划分，可以解决多目标间评价标准难以统一的问题，最终的比较结果也显示优化方案的土地利用结构综合满意度(2.87)明显高于现状方案(2.80)以及自然演化方案(2.23)的综合满意度,此方法对于土地利用规划的编制具有一定的借鉴意义。

2)以曲周县作为研究实例，对比3种方案的土地利用结构变化情况以及最终的评价结果可以发现耕地、林地、城镇村及工矿用地、未利用地4种地类之间的结构变化是影响评价结果的主要因素，其余地类囿于对目标效益贡献不显著以及用途难以转换等特性，对于评价结果的影响程度较低。因此，结合区域土地利用优化目标，保持其余地类结构的相对稳定，协调平衡耕地、林地、城镇村及工矿用地、未利用地间的结构比例是区域土地利用结构优化的基本途径。

3)对曲周县实证研究发现，对土地利用结构进行优化后的结果为：耕地面积53 354.72 hm2，园地面积306.23 hm2，林地面积644.93 hm2，草地面积350.00 hm2，城镇村及工矿用地9 073.24 hm2，交通运输用地2 075.17 hm2，水域及水利设施用地1 670.00 hm2， 未利用地193.8 hm2。

3.2 讨 论

1)多目标规划模型以及模糊分析方法存在着主观性较强的特点，其关于效益的核算方法是否可以体现出区域的发展特性有待商榷；另外土地利用过程是一个处于长期性变化的复杂过程，土地利用系统中的要素也在时刻的变化，多目标下的土地利用结构定量优化缺乏时间弹性，因此如何将土地利用的敏感性变化同土地利用结构优化进行整合研究，是值得探索的新命题。

2)本研究进行的土地利用结构优化是基于区域未来理想状况下的一种模拟性的合理安排，兼顾区域经济、社会和生态等效益，但是由于土地利用系统及目标的复杂性、不确定性和动态性特性，区域土地利用需求变化下优化的配置方案和真实的优化需求间会存在一定的偏差，为提高优化方案的现实匹配程度，对优化方案进行不同的情景设置，模拟情景条件，是未来研究的一个主要出发点。