实现公平而有质量的义务教育的最低成本测算——以H省B县小学为例

李祥云，周 云

教育公平是最基本的社会公平，而义务教育公平又是教育公平的基础。改革开放40年来，我国政府采取诸多措施致力于义务教育公平的实现，从确保每个适龄儿童都有学上，到每个学生均享有平等的教育资源，我国在义务教育公平方面取得了巨大的成就。伴随着县域内义务教育资源配置公平的逐步实现，民众对义务教育公平又有了更高层次的追求，即要求提升义务教育质量，追求教育结果公平。为回应民众对更高层次教育公平的诉求，党的十九大明确提出“努力让每个孩子都享有公平而有质量的教育”。所谓“公平而有质量”的义务教育，是指每所学校均应让学生达到一定的质量标准，并且该质量标准要与每个学生平等地接触高等教育和就业机会所需要的知识和技能相匹配。与受教育权公平和教育资源配置公平相比，公平而有质量的教育强调的是教育结果公平，属于纵向公平，教育资源投入更有利于弱势群体。因为要使弱势群体的学生达到同样的教育结果，需要为他们提供比普通学生更多的教育资源。然而，要将党的十九大提出的这一理念变成可以执行的政策，必须要解决两个关键问题：一是确立学校应达到的教育质量标准；二是估算学校达到设定的教育质量标准所需的最低成本。学校的教育质量体现在学生对科学知识的掌握程度和学校对学生德育、体育、美育和生产劳动教育等素质品质的培养程度两方面。其中，学生对科学知识的掌握程度可以通过标准化课程考试成绩来测量，而素质品质的培养程度不易测量。在此，我们采用了国外已有研究的处理方法，假设学生对科学知识的掌握程度与学生素质品质的培养程度存在高度正相关的关系，学校教育质量标准或学生成绩标准由当地教研室给定。在此基础上，本文以H省B县小学为例，运用成本函数法对B县所辖每一所小学达到给定教育质量标准所需最低教育成本进行测算，以此来考察县域内实现公平而有质量的小学义务教育究竟还需要增加多少财政投入。本文旨在为测算义务教育学校达到“公平而有质量的教育”要求所需的最低成本，在方法上提供一个可借鉴的案例。

一、测算达到一定质量标准的教育成本的方法

从已有的国外文献来看，目前测算学校达到一定质量标准所需教育成本的方法主要有以下三种：一是成功学校法，又称经验证据法。即通过事先确定一个教育质量标准，筛选出已经达到该教育质量标准的成功学校，确定其投入的要素类别与价格，并测算其成本，在此基础上根据各学校实际需求对成功学校的成本进行调整，得到各学校达到设定教育质量标准所需的最低成本。二是专家判断法，又称之为资源成本模型法。该方法是通过成立具有丰富教学经验的专家小组，由专家小组确定达到一定质量标准的“原型学校”所需的教学资源和教学策略，确定投入要素的数量和价格后计算得到实现教育质量标准所需最低成本，然后对该成本进行调整，以满足不同环境学校达到教育质量标准所需要的实际经费。三是成本函数法。成本函数法是先设定一个成本函数方程，因变量为生均成本，自变量以学校是否可以自主调节和控制为标准，分为学生成绩、资源价格等可控因素以及学校规模、特殊学生需求等不可控因素两类，采用各自变量的实际观测值代入到方程中进行回归得到各变量的回归系数。在单一变量的情况下，将设定的学生成绩代入到方程中，即可得出达到一定教育质量标准所需投入的最低成本。

成功学校法在理论上提供了测算达到一定教育质量标准所需最低教育成本的一个比较清晰的思路，但在实践上存在一定的困难：一是难以找到符合标准的成功学校。当教育质量指标制定得越高时，符合条件的成功学校就越难找。二是难以找到确定各成功学校权重的标准。将各成功学校投入的教育成本进行加权平均的目的在于要抹平各成功学校的自身差异，使得测算出的基础成本具有代表性，然而在实践中缺乏确定权重的标准与理论依据。专家判断法通过专家小组设计出一个原型学校进行教育成本测算，其缺点在于专家判断法过于依赖专家的主观判断。某个教育资源是否是达到教育质量标准的学校所必需的，以及该资源需要投入多少，都是来自专家的主观经验判断，而经验判断常常具有很大的不确定性。相比较之下，成本函数法虽然被一些人批评将教育过程视为一个黑箱，没有公开所投入的教育成本如何使用的细节，以及成本函数法在技术上的复杂性难以理解，但是成本函数法使用影响教育成本的因素的实际数据去测算学校达到教育质量标准所需的教育成本，其结果更准确，准确的测算结果有助于决策者制定更加精准的政策。因此，本文将采取成本函数法来测算学校为达到一定教育质量标准所需投入的最低教育成本。

二、模型设定、指标构造与数据来源

本部分将设定测算义务教育学校达到教育质量标准所需最低成本的成本函数模型。影响教育成本的因素主要包括学生成绩、资源价格、学生需求以及学校规模等。由于处于不同环境的学校购买相同的资源存在价格差异，如果不对其进行调整，将会导致最后测算出的教育成本不准确。由于学校投入的主要资源是教师，学校间的资源价格差异主要通过教师的招聘成本来反映，弄清学校间招聘一名同质教师所需成本差异尤为重要。因此，我们的成本函数模型构建分为两步：第一步，建立教师工资模型，通过该模型得到反映不同环境下学校聘请一位同质教师所需支付的基本工资差异的教师成本指标，并用该指标作为总成本函数中的资源价格的代理指标，以对总成本进行调整；第二步，建立总成本函数模型，进一步对因学生的需求和学校规模不同造成的学校达到给定质量标准所需成本的差异进行调整。

(一)模型设定

1.教师工资模型

我们将决定教师工资的因素以学校是否可以自主控制和调节为标准分为两大类，一类为可控因素，包括学生成绩、教师学历、教师职称、教师的教学经验等；另一类为不可控因素，包括学校规模、特殊学生需求、地理环境等。基于此，本文构建了以下教师工资模型：

avgwagei=α0+α1outcomesi+α2degreei+

α3protitlei+α4exprti+α5sclenri+α6Pavgpoori+districti+εi

(1)

式(1)中，i代表学校，avgwagei为i学校实际平均教师工资，outcomesi为i学校的生均成绩，degreei为i学校教师的平均学历，protitlei为i学校教师平均职称，exprti为i学校教师平均教学经验，sclenri为i学校规模，Pavgpoori为i学校困难学生占比，districti为反映i学校是位于农村地区还是城镇地区的虚拟变量，εi为随机扰动项。

教师工资的组成部分之一为绩效工资，而学校分配绩效工资是否与学生成绩挂钩、绩效工资是否会反过来影响教师的教学积极性进而影响学生成绩尚不明确，若绩效工资与学生成绩之间存在这种双向因果关系，则通过最小二乘回归得到的系数是有偏的。因此，为检验二者之间是否存在双向因果关系，我们在此选取学生成绩的工具变量，通过两阶段最小二乘法来估计教师工资模型，并将回归结果与最小二乘法回归结果进行对比。由于不同县镇之间学校的教学环境与质量可能会存在较大的差异，并且不同县镇的考试内容与评分标准无法做到统一，因此用临近县镇学校学生的期末成绩作为工具变量就不具有说服性；而除去每个镇内的中心小学，位于一个镇农村地区的学校大致处于相同的地理位置和外部环境，其学校特征更加相关。因此，我们将每个镇上中心小学的成绩保持不变，将镇上农村地区各小学的成绩按其离中心小学的距离进行等距互换，将此作为工具变量进行两阶段最小二乘回归，即：

第一阶段：

outcomesi=α0+α1outcomesi′+α2degreei+

α3protitlei+α4exprti+α5sclenri+α6Pavgpoori+districti+εi

(2)

第二阶段：

avgwagei=α0+α1outcomesi+α2degreei+

α3protitlei+α4exprti+α5sclenri+α6Pavgpoori+districti+εi

(3)

2.总成本模型

通过教师工资模型测算出不同学校聘请一名同质教师所需支付的预测教师工资后，我们用预测工资作为资源价格的代理变量测算为达到一定教育质量标准所需的最低生均成本。在总成本模型中，因变量是生均成本，自变量包括资源价格、学生特征和学校的教育环境。在学生特征方面，首先，对于学生成绩，县教研室要求学生成绩达到及格(60分)和要求学生成绩达到优秀(80分以上)，不同标准对应的学校教育资源投入水平是不一样的，即设定学生成绩标准越高，所需教育资源水平和教育成本也越高。此外，由于不同学生在家庭背景、天赋等方面都存在差异，具有特殊需求的学生一般需要额外的资源支持才能达到设定的成绩标准，用困难学生占比反映不同学校学生特殊需求。另外，学校的教育环境也可能会影响总成本，包括学校的招生规模、学校所处的地理位置等等。确定了影响总成本函数的因素之后，借鉴Duncombe和Yinger(2011)的建模思路，构建学校教育总成本模型为：

Avgstuexpi=β0+β1wagei+β2outcomesi+β3Pavgpoori+β4dis+εi

(4)

式(4)中，i为学校，因变量Avgstuexpi为i学校生均支出；自变量wagei为教师工资模型中测算出的i学校平均教师工资，outcomesi为i学校生均成绩，Pavgpoori为i学校的困难学生占比，dis为反映i学校规模的虚拟变量，εi为随机扰动项。在该模型中，我们重点关注教师工资和学生成绩回归系数的方向。由于教师工资占学校教育投入的绝大部分，因此，如果要达到一定的教育质量标准而增加教育投入，我们预计要增加在教师工资支出，即β1>0；在一般情况下，提高学生的成绩标准意味着需要投入更多的教育资源，因此随着学生成绩标准的提高，教育成本投入要增加，即β2>0。

(二)指标构造与数据来源

本文用于实证研究的数据是基于对H省B县小学的调研数据整理得来，以下将详细解释模型中各指标构建和主要数据来源。

1.学生人数

2.学生特征

(1)学生成绩。我国义务教育小学分为六个年级，且语文与数学为核心课程。在低年级(一、二年级)，学生成绩受初始资源禀赋的影响比较大，学校教育对学生个人层面上的影响不够突出，而三年级作为一个承上启下的中间年级，三年级学生的成绩在一定程度上较好地反映学校教育对学生成绩的影响。此外，由于六年级是毕业年级，六年级的成绩除了能够最大程度反映学校教育投入对学生成绩的影响之外，还直接关系到升学，具有重要性。因此，我们选取了每个学校三年级和六年级学生期末考试的语文平均成绩和数学平均成绩作为学生综合成绩的衡量标准，通过对年级和课程赋予相应的权重计算得出每个学校在一定教育支出水平下的综合成绩。在小学，由于不受分科等因素的影响，核心课程具有相同的重要性，于是我们将每个年级的语文和数学平均成绩分别赋予0.5的权重，计算得出每个年级的综合成绩。由于年级越高，在校受教育的时间就越长，就越能体现学校教育对个人实际能力的影响，并且六年级的成绩直接关系到小学毕业和中学入学所要求达到的成绩，因此我们将三年级和六年级的综合成绩分别赋予0.2和0.8的权重，通过计算得出全校的综合成绩，即：outcomesi=0.2×(0.5Ci3+0.5Mi3)+0.8×(0.5Ci6+0.5Mit)，其中，outcomesi为i学校的综合成绩指标，Ci3为i学校三年级语文平均成绩，Ci6为i学校六年级语文平均成绩，Mi3为i学校三年级数学平均成绩,Mi6为i学校六年级数学平均成绩。

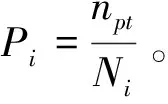
3.教师人数

我们主要根据各学校提供的教师信息作为参考。提高学生成绩是一个长期的过程，因此为提高学生成绩而进行的投资也应该是一种长期投资。由于各学校投入的教育资源主要是教师，因此在本研究中，使用的教师人数是各学校的专任教师数，即具有教师资格证书、专门从事教育工作的教师人数。

4.教师特征

(1)实际平均教师工资。教师工资由多个部分组成，其中，基础工资反映了教师的学历和职称，津贴反映的是教学年限和地理环境不同给予教师特有的补贴，绩效工资反映教师的工作量或者与学生成绩挂钩。此外，学校还要为教师缴纳社保和公积金。我们用基础工资、津贴、绩效工资、社保和公积金五项作为教师工资的组成部分，通过加权平均得到每个学校实际平均教师工资。

(2)预测平均教师工资。由于要求学校达到一定的教育质量标准需要为其提供最低水平的教育资源，因此必须考虑学校之间投入资源的价格差异。学校投入的教育资源包括师资、办公用品、教学设备等。其中，办公用品、教学设备等资源的价格都是由市场确定，县域内学校之间的价格差异不大，而除受学历、职称、教学经验等可控变量的影响之外，由于不同地区交通、地理位置等生活成本和学校规模等不可控变量，不同地区学校聘请一名同质教师的成本存在较大的差异，因此需要构建一个教师工资模型将可控变量对于教师工资产生的影响从不可控变量对学生成绩产生的影响中分离出来。将每个可控变量的县平均值和每个不可控变量的校实际值代入到教师工资模型中，就得到了预测平均教师工资，即：wagei=β1iX1i+β2iX2i。其中，wagei为i学校的预测教师工资，X1i为影响i学校教师工资的可控因素，包括学生成绩、教师学历、职称和教学经验等，β1i为影响i学校教师工资的可控因素的回归系数，X2i为影响i学校教师工资的不可控因素，包括学校规模、困难学生占比、地理位置(城镇或农村)等，β2i为影响i学校教师工资的不可控因素的回归系数。

5.学校特征

(1)地理位置。我们调研的是H省B县小学，通过每所学校所处的地理位置，对每个镇内的学校进行分类，分别为位于农村地区的学校和位于城镇地区的学校，并将此作为一个虚拟变量，当学校位于农村地区时，赋值为1，即：districtt=1；districti=0，学校位于城镇地区。

(2)学校规模。在计算教师工资模型时，我们将每个学校参加期末考试的学生数作为学校规模。在计算总成本模型时，我们以0-100人、100-200人以及200人以上将学校规模分为三部分，并引入虚拟变量：若学校规模为100-200人，令ds1为1，其它规模为0；若学校规模为200人以上，令ds2为1，其他规模为0。

6.生均成本

学校教育成本包括三类：一是教师工资，如前所述包括基本工资、津贴、绩效工资、社保和公积金五大类，我们在总成本模型中采用的教师工资是经过教师工资模型调整后的预测教师工资；二是公用经费，即为改善师生教学工作和学习环境所支出的各类费用，包括商品服务支出、维修费、培训费、房屋建筑物构建、办公设备购置等；三是用于学生的各种补助经费。将这三类经费加总，并除以学生数，即为每个学校的生均支出。

以上各变量的描述性统计见表1。由表1可以看出，在我们调研的所有学校中，从总体上看，各校的学生人数、教师人数、实际平均教师工资和生均成本的标准差很大，说明不同地区学校在规模、教育资源投入和教育成本投入上存在很大的差异；从平均值可以看出，学生成绩总体位于及格水平，每个学校的困难学生占比为50%左右，教师的平均综合特征为拥有大专学历、一级职称以及15年左右教龄。具体来看农村学校和城镇学校各指标之间的差异，主要体现在以下两点：一是地区间生均成本差异较大。农村学校的平均生均成本为17703元，是城镇学校生均支出的2.05倍，这可能是由于城乡学校规模差异太大所导致的(城镇学校的平均规模为1354.867人，为农村学校规模的7.86倍)，由于农村学校规模较小，而每门课程又必须要配备一定数量的老师，导致学校的师生比高于城镇学校，较高的师生比意味着学校要承担更高的生均成本。此外，随着规模的扩大，学校也可能会出现规模经济。二是地区间学生成绩差异较大。农村学校的学生平均成绩为63.3，远低于城镇学校的学生成绩71.6。出现这种现象可能的原因是农村学校的困难学生占比比城镇学校的困难学生占比要高，困难学生从家庭中获得的教育资源较少，在学习能力等方面与普通学生相比可能存在差距。此外，困难学生占比也可以反映一个地区的贫困程度，一般来说，困难学生占比越高，该地区的贫困率就越高，而贫困率又与较低的教育水平相关。

表1 描述性统计

三、实证结果与分析

(一)教师工资模型与教师工资指数的估计

为了筛选出拟合程度最高且最能显示各数据之间相关程度的模型，我们最终将教师工资模型中除虚拟变量以外的其他变量的数值取对数代入模型中回归。表2给出了三个教师工资模型的回归结果，前两个模型运用最小二乘法进行回归，差异在于是否将影响教师工资的不可控因素(学校规模、困难学生占比和学校的地理位置)放入模型中，第三个模型选取学生成绩的工具变量进行两阶段最小二乘法回归。从整体上看，第一、第三个模型回归得出的回归系数的方向是一致的，并且各回归系数均在1%水平上显著。在每个模型中，学生成绩、教师职称和教师学历三个变量的回归系数都相对较大，且对教师工资有显著正影响，这与预期和国内外已有研究的结果一致(Figlio and Kenny,2007；胡咏梅和杜育红，2009；薛海平和王蓉，2010)，即学生成绩越高，对教师质量要求越高，相应聘用教师的成本也越高，而反映教师质量的核心指标是教师的学历和职称。同时这也与我国的实际工资结构相符合，占我国教师工资较大比重的基础工资主要是由职称和学历决定的，部分津补贴和福利也与学历和职称挂钩。第二，表2中第(2)列为式(1)最小二乘法的回归结果，第(3)、(4)列为式(2)、式(3)两阶段最小二乘法的回归结果，对比两种方法的结果可看出，两种方法的回归结果在回归系数的数值、方向以及显著性上具有高度的一致性，并且在拟合程度上也完全相同。因此我们认为，没有明显的证据证明教师工资与学生成绩之间存在双向因果关系。第三，对比表2第(1)、(2)列的回归结果可知，不可控因素的加入提高了模型的拟合程度。在不可控因素中，学校规模对数值的回归系数符号为负，学校规模每扩大1%，师均工资将减少0.022%，出现这个结果可能的原因是学校存在规模效应，学校的规模越大，其教育效率越高，因此不需要投入与较小规模时等比的教育资源来提升相同的成绩标准。回归结果还显示，困难学生占比越高，教师工资越高。一般来说，困难学生占比可以在一定程度上反映一个地区的贫困率，贫困率越高的地区工作环境会更加艰苦，因此这些地区的学校必须支付更高水平的工资来吸引和聘请优秀的教师。另外，相比于城镇学校，农村学校的教师工资水平较高。造成该现象可能的原因有两点：一是农村相比于城镇吸引年轻师资的能力比较弱，因此农村学校教师的年龄普遍偏大，这也可以从表1中我们统计的教师工作年限中得以证实(农村学校教师的平均工作年限为15.31年，而城镇学校教师的平均工作年限为14.40年)。一般来说，工作年限越长，教师职称越高，教师的基础工资和教龄津贴也越高。二是在我国，农村学校教师获得的补助，例如高寒补助等，会比城镇地区教师获得的补助要多，因此农村学校教师的平均工资水平会比城镇学校教师的工资水平相对较高一些。

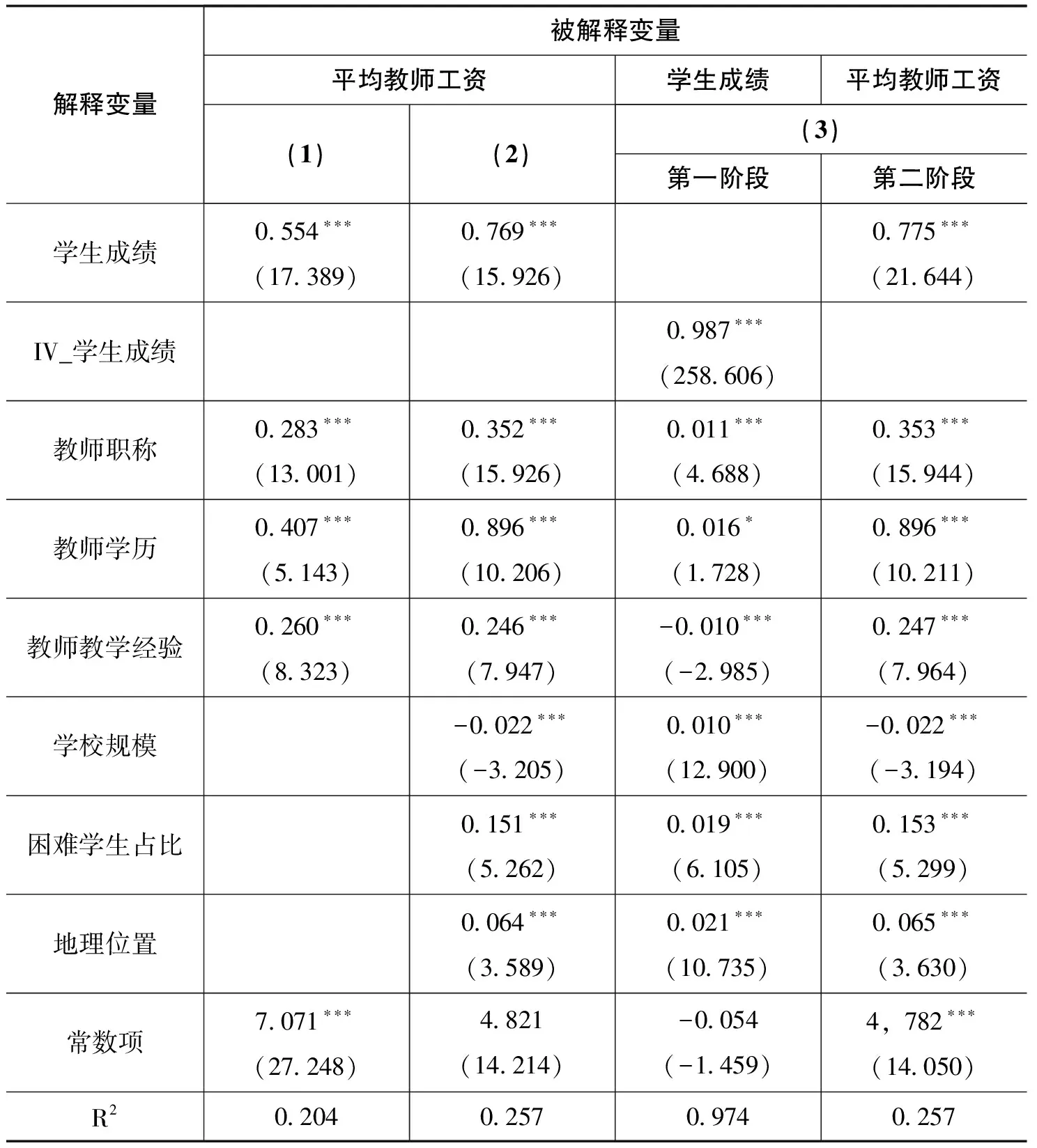
表2 教师工资模型回归估计结果

注：1.*、***分别表示10%、1%显著水平；2.括号内数值为t值。

估计教师工资模型的目的是为了将影响教师工资的可控因素从不可控因素中分离出来，制定学校吸引具有既定特征教师所必须支付的基本工资指标，该基本工资指标只衡量不可控因素的变化。因此，根据表2第(2)列教师工资的回归结果，我们将学生成绩、教师职称、学历和教学经验等可控变量的回归系数与该变量的平均值相乘，并把得到的结果添加到回归的截距项中，得到的结果是所有学校都一样的单一数值；将学校规模、特殊学生需求和地理位置等不可控变量的回归系数与该变量的实际值相乘，得到的结果在不同的学校之间有所不同。将二者加总，便得到每个学校预测教师工资的对数值，将该值取反对数，即为调整后的每个学校的预测教师工资。为制定教师工资指标，我们引入普通学校的概念，即该学校所有影响教师工资的变量都处于县平均水平，将这些变量的县平均值分别与回归系数相乘，加总得到的结果并取反对数，便得到普通学校聘请一名优秀教师所需要的成本。用测算出的预测教师工资除以普通学校的教师工资，再乘以100，即得到教师工资指标，该指标反映了不同学校聘请一名同质教师的成本差异。根据我们测算的教师工资指标的结果显示，将近有70%的学校的教师工资指标大于100，反映出大多数学校都需要支出比普通学校更多的经费来聘请一名同质的教师。我们按学校所处的地理位置将学校分为城镇学校与农村学校两类，分别计算了城镇学校与农村学校的教师工资指数，结果如图1所示。由图1可知，城镇学校的教师工资指标为91.8，农村学校的教师工资指标为104.5，农村学校比城镇学校要多花将近13%的县师均工资才能聘请到一位同质的教师。

图1 城镇学校与农村学校聘请一名同质教师的工资指标

(二)总成本模型

得到预测教师工资后，我们就可以用它作为资源价格的代理变量，估计总成本模型。我们回归了两个总成本模型，这两个模型的差别在于是否将可能影响生均支出的不可控因素加入到模型中，回归结果分别为表3第(1)、(2)列所示。由回归结果可看出，对于不加入不可控因素的模型(1)，教师工资和学生成绩的回归系数均在1%水平上对生均支出有显著正影响，并且教师工资的回归系数要远大于学生成绩的回归系数，说明教师工资对于生均成本的影响要更大。随着不可控因素加入总成本模型中，可决系数R2的值由0.482增大至0.525，解释变量对被解释变量的解释力度增强。式(4)的回归结果如表3第(2)列所示，其回归模型的系数与预期基本上是相符的。其中，学生成绩在1%水平上对生均成本具有显著正影响，说明学生成绩越高，所需的教育成本越高。预测教师工资对生均成本也具有显著的正向影响，且预测教师工资的回归系数是所有影响生均成本因素的回归系数中最大的——预测教师工资每增加1%，生均支出将增加3.554%，这表明学校教育成本有很大一部分用于教师工资。在学生特殊需求方面，较高的困难学生占比与生均成本呈正相关，且在1%水平上显著，困难学生占比每提高1%，生均支出将提高0.816%。另外，学校规模虚拟变量dis1和dis2的回归系数分别为-0.173和-0.310，且均在1%水平上显著。这意味着相比于规模为100人以下的学校的生均支出水平，随着学校规模扩大，生均支出将会逐渐下降，并且由于dis2回归系数的绝对值大于dis1回归系数的绝对值，当学校规模扩大至200人以上后，生均成本下降的幅度将会变大，这个结果与Smet(2001)研究的结果是一致的，即不考虑私人教育成本，学校公共教育支出与学校规模呈“L”型。

表3 总成本模型OLS回归估计结果

注：1.***表示1%显著水平；2.括号内数值为t值。

(三)达到一定教育质量标准所需的最低教育成本测算

在得到总成本函数之后，我们将利用总成本函数来制定成本指标，测算各学校达到一定教育质量标准所需投入的最低教育成本。需要注意的是，对达到一定教育质量标准所需投入的教育成本测算仅限于实际成绩低于设定成绩标准的学校的成本测算，对于没有达到教育质量标准的学校，若测算的教育成本与实际教育支出的差额为正，则代表该学校需要额外的教育财政拨款；若差额为负，则表示在资源更加有效配置和利用的条件下，该学校的教育支出已经足以支付达到一定教育质量标准所需要的教育支出，因此不需要再对该学校进行额外的教育拨款。在测算达到一定教育质量标准所需要的教育成本以及成本指标时，我们引入基准学校和普通学校的概念。基准学校是指除学生成绩外，其他影响教育成本的因素均处于平均水平的学校，基准学校教育成本的测算是将除学生成绩以外的总成本模型中变量的回归系数与该变量的平均值相乘，并将得到的结果添加到截距项中；将设定的成绩标准与学生成绩的回归系数相乘，加总二者得到的结果，并将其取反对数，即为基准学校测算的教育成本。普通学校是指所有包含在总成本函数模型中的变量均处于县平均水平的学校，普通学校的教育成本测算是将所有变量的回归系数与该变量的县平均值相乘，加总并添加到截距项中，将得到的结果取反对数，即为普通学校的教育成本。

成本指标旨在衡量不可控变量对达到设定的教育质量标准所需最低教育成本的影响，其制定方法与教师工资指标的制定方法类似。第一步，将模型中所有可控变量(即预测教师工资和学生成绩)的回归系数乘以该变量的平均值，加总得到的结果，并将其添加到回归的截距项中，得到的是所有学校都不变的单一数值；第二步，将模型中所有不可控变量(即困难学生占比和学校规模)的回归系数乘以该变量的实际值，并将所有的结果加总，不同的学校得到不同的结果；第三步，加总第一步和第二步中得到的结果，即得到预测生均支出的对数，对该对数取反对数便可计算出每个学校的预测生均支出；第四步，将每个学校的预测生均支出除以普通学校的测算支出，再乘以100，即可获得教育成本指标。将教育成本指标与基准学校测算的教育成本相乘，再与学生人数相乘，即得到每个学校达到教育质量标准所需的最低教育成本。

根据我们测算出的教育成本指标结果显示，在我们调研的学校中，有95%以上的学校的教育成本指标在100以上，说明绝大多数学校要达到设定的教育质量标准所需的最低生均成本都高于普通学校的生均成本。其中，成本指标最大的为251，最小的为91，表明成本指标最大的学校要比成本指标最小的学校多花两倍多的生均成本才能达到相同的教育质量标准。我们以100人与200人为界线将学校规模划分为100人以下、100-200人以及200人以上三类，测算每一规模下学校的教育成本指数，结果如图2所示，可以看出规模越大的学校达到教育质量标准所需的生均支出就越少。我们按学校所处的地理位置将学校分为城镇学校和农村学校两类，分别测算城镇学校和农村学校的成本指标，结果如图3所示，城镇学校的成本指标为118.7，农村学校的成本指标为170.4，说明农村学校对每个学生要多花40%左右的成本才能达到与城镇学校相同的教育质量标准。

图2 不同学校规模下的教育成本指数

图3 不同地区学校的教育成本指标

由表1可知，我们调研的B县小学的平均成绩为65.8分。根据当地县教研室认可标准，测算了当成绩指标设定为80分、85分和90分时，基准学校的教育成本分别为13322.7元/人、13658.9元/人和13983.5元/人。根据回归结果，我们测算了2018年B县小学达到县设定的教育质量标准所需的教育成本，在计算过程中发现，有部分学校实际投入的教育成本要高于达到一定教育质量标准所需的最低教育成本，因此我们将保持这些学校的实际教育成本不变进行测算，结果如表4所示：从整体上来说，当学生成绩标准设定为80分时，每所学校所需最低生均成本为16767.3元，比实际生均成本高91.85%；全县义务教育学校所需最低教育成本为4.448亿元，其中，有86%的学校实际教育成本低于达到成绩标准所需的最低教育成本，这些学校一共需要额外增加教育拨款2.054亿元，占实际投入教育成本的88.6%。当成绩标准设定为85分时，每所学校所需最低生均成本为17190.4元，比实际生均成本高出96.7%；全县义务教育学校所需最低教育成本为4.561亿元，其中，有88%的学校实际教育成本低于达到成绩标准所需最低教育成本，这些学校一共需要额外增加教育拨款2.173亿元，占实际投入教育成本的93.7%。当学生成绩标准设定为90分时，每所学校达到该成绩标准所需的生均成本为17599.0元，比实际生均支出高101.4%；全县义务教育学校所需最低教育成本为4.669亿元，其中，有88%的学校实际教育成本低于达到成绩标准所需最低教育成本，这些学校需要额外增加教育拨款2.288亿元，占实际投入教育成本的98.7%。从测算的城镇学校和农村学校达到一定教育质量标准所需最低教育成本来看，随着设定的成绩标准的提高，城镇学校的生均支出均低于农村学校，可能的原因是规模经济；城镇学校所需要的额外支出远高于农村学校，可能的原因是城镇学校规模较大。

表4 2018年B县小学达到一定教育质量标准所需教育成本测算结果

四、结论与政策建议

本文运用成本函数法测算县域内每所小学达到县教研室给定教育质量标准所需的最低教育成本。结果发现，由于资源价格、特殊学生需求、学校规模等影响因素的差异，不同学校达到县教研室设定的教育质量标准所需最低的教育成本有很大的差异，根据回归与测算结果，主要得出以下结论：一是学生成绩、教师工资和特殊学生需求均对教育成本具有正向的影响，学校规模对教育成本有负向的影响，不同学校达到设定的教育质量标准所需的最低教育成本不同。教师作为学校主要投入资源，教师工资对教育成本的影响最大，且不同地区学校聘请一名同质教师所需要的成本也相差较大，农村学校相比于城镇学校所需要的成本更高；二是设定的成绩标准越高，所需投入的教育成本就越多。在设定的成绩标准下，绝大多数学校现有支出水平远低于达到设定成绩标准所需的最低教育成本或支出水平，这说明县域内小学的教育财政投入还不够充足；三是通过成本指标的测算可以发现，除县城学校的成本指标低于100以外，镇所在地学校和农村学校的成本指标均大于100，且农村学校的成本指标要高于城镇学校，在达到相同的教育质量标准之下，农村学校需要花费的生均成本或支出更多；四是有10%左右的学校实际投入的教育成本要高于达到一定教育质量标准所需的最低教育成本，且其中绝大多数学校都位于农村地区，说明学校在使用教育经费的过程中存在低效率的问题。

基于以上的研究结果，本文提出如下几点政策建议：一是本研究表明，实现党的十九大提出的“努力让每个孩子享有公平而有质量教育”，需要额外增加财政支出。值得注意的是，若把成绩标准从及格(60分)提升到优秀(80分以上)时，所需增加的财政支出为原来的一倍左右，这会给地方财政带来较大的压力，故义务教育学校质量或成绩标准政策设定，需要充分考虑我国财政承受能力。二是要确保县域内每一所学校的学生均达到政策设定的教育质量标准，需要对农村学校和城镇学校采取差异化的拨款标准，即对条件艰苦、特殊需求学生多、规模小的农村学校给予远高于城镇学校的生均拨款水平。三是鉴于县级财力有限，实现公平而有质量的义务教育需要大幅度提高财政支出水平，故需要进一步强化中央和省级政府的义务教育支出责任，即适当提高中央和省的义务教育支出分担比例。四是建立和完善我国义务教育质量监测体系，引入问责制，促使学校更加有效率地使用教育财政资金。