软岩巷道锁拱锚杆精细化数值模拟研究

管清升 ，杨 博 ，王德超 ，李为腾 ，梅玉春 ，杨 宁 ，马海曜

（1.山东科技大学 山东省土木工程防灾减灾重点试验室，山东 青岛 266590；2.济南轨道交通集团有限公司，山东 济南 250101；3.江苏建筑职业技术学院，江苏 徐州 221116）

随着浅部煤炭资源的枯竭，煤矿开采向深部发展已成为必然趋势。由于软岩巷道围岩承载特性差、力学环境复杂、流变特征显著，致使巷道变形量大，支护构件容易发生破坏，难以保证长期稳定。软岩巷道支护已成为制约煤矿安全高效开采的重要技术难题[1-2]。目前，锚杆-拱架（拱形支架）联合支护是常见的软岩巷道支护形式。这种支护形式是在常规锚网喷支护的基础上增加拱架支护，形成刚柔相济的完整支护体系。拱架的主要形式是U 型钢，目前以U36 为主；此外，钢管混凝土拱架也逐渐发展起来，其承载力是U36 型钢拱架的2 倍以上[3-4]。

然而，随着软岩巷道支护难度的不断增加，拱架大变形及屈曲失效的问题仍时有发生。对此，常在拱架发生大变形的部位增设锁拱锚杆。目前，谢文兵[5-6]、荆升国[7-8]分析了U 型钢支架失稳的原因，研究了支架-锚杆（索）协同作用机理，强调棚-索补强控制理念，提出了U 型钢支架-锚索耦合支护技术；罗彦斌[9]、陈丽俊[10]分析了隧道硐室锁脚锚杆与拱架间的联合承载机制，优化了锁脚锚杆参量。但是，上述研究并不能作为锁拱锚杆的位置、长度等参数设计的理论依据。此外，在软岩-支护作用机制分析手段中，理论分析局限性明显，模型试验成本高、操作困难，数值模拟最为常用。学者在模拟中以围岩特性为主，对支护构件力学行为考虑不足，如FLAC3D中的beam 单元和cable 单元常用来模拟拱架和锚杆，但都不具备合理的失效行为，支护构件承载能力被放大，模拟精度较低。对此，首先介绍了最新开发的锚杆-拱架联合支护精细化模拟技术，以梁家煤矿典型软岩巷道为工程背景，开展了以锁拱锚杆安设位置、长度为变量的数值模拟试验，分析了锚杆-拱架联合支护的失效过程，对比研究了不同锁拱锚杆参数与巷道支护效果关系，确定了优化设计方案并进行现场验证。

1 锚杆-拱架联合支护精细化数值模拟技术

在锚杆-拱架联合支护的FLAC3D数值模拟中，用自带beam 单元模拟拱架时，发现拱架屈服失效不受轴力影响而仅与弯矩有关，轴力可无限增加，这与工程实际不相符。针对此缺陷，以拱架截面的压弯极限承载力为拱架屈服判据，进行了beam 单元的修正和后续完善[11-12]。用自带cable 单元模拟锚杆时，发现当杆体变形很大时轴力始终保持恒定，无法发生破断。针对此缺陷，建立了锚杆破断判据，实现了锚杆破断失效的模拟[13-14]。

随着对数值模拟精度要求的不断提高，发现beam 单元建模的拱架与围岩之间的相互作用也需改进，因此建立了拱架-围岩相互作用模型，实现了拱架与围岩法向可脱离、轴向可滑移的有效模拟[15]。目前，开发的锚杆-拱架联合支护精细化模拟技术主要包括3 个模块，精细化数值模拟技术的3 个模块如图1。

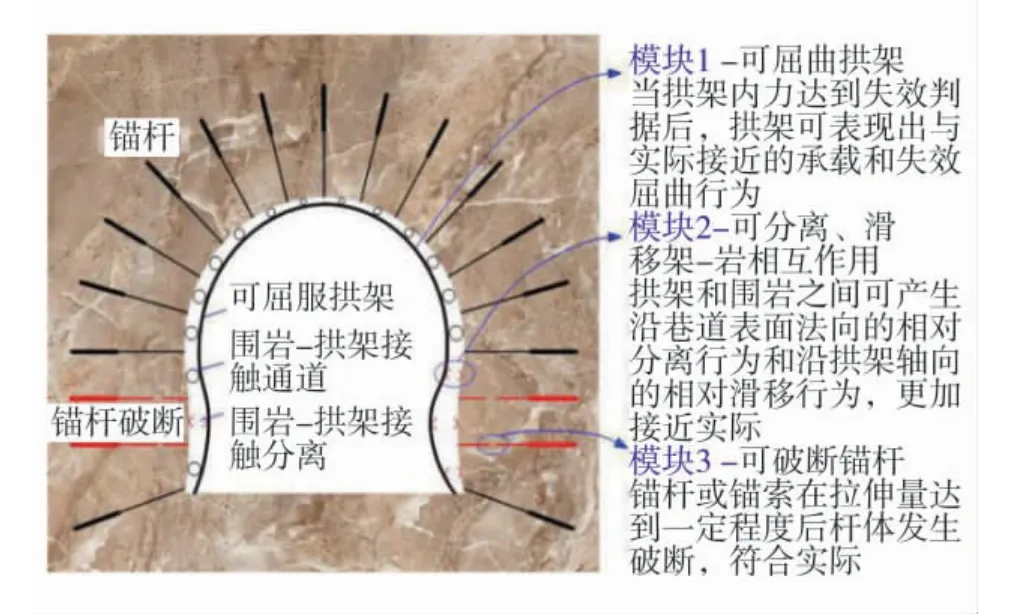
图1 精细化数值模拟技术的3 个模块Figure 1 Three modules of refined numerical simulation technology

1）可破断锚杆（索）模块。在自带cable 单元中引入锚杆（索）失效破断判据，见式（1）。

式中：S 为锚杆自由段长度；Smax为锚杆自由段极限长度，由自由段初始长度和极限伸长率决定。当自由段长度小于Smax时，杆体轴向力学模型为自带的理想弹塑性模型；当杆体自由段长度超过极限长度Smax时，通过FISH 程序使锚杆极限轴力与轴向刚度均变为0 且恒定，从而实现锚杆杆体破断[13-14]。

2）可屈服拱架模块。以拱架截面压弯极限承载力计算公式作为拱架屈服失效判据，该修正判据以特定函数的形式将轴力N 纳入屈服判据，使判据表达式界定出包含弯曲和轴压因素的屈服包络范围，若内力超出此范围，则拱架单元发生屈服[12]。

式中：m、n 分别为弯矩系数和轴力系数，m=M/Mu，n=N/Nu；M、N 分别为 beam 单元的弯矩和轴力；Mu为梁构件在纯弯曲作用下的极限弯矩；Nu为柱构件在轴压作用下的极限轴力。

3）拱架-围岩相互作用模块。提出了拱架-围岩法向分离判据，通过手动修改拱架节点与围岩之间link 连接的参数，改进了拱架-围岩相互作用的本构关系，使拱架在围岩接触面法向可与围岩分离，在接触面切向可发生相对滑移[15]。

2 数值试验方案

2.1 典型案例概况

山东龙口市梁家煤矿属于典型三软地层，主采1#煤层、2#煤层和4#煤层。其中4#煤层厚度13.7 m，结构极为复杂，稳定性差。4#煤层巷道典型断面直接顶主要为炭质泥岩及泥岩夹黏土岩，易风化脱落，吸水膨胀，下沉量大，属易垮落顶板；直接底板为0.65 m 泥岩，局部为炭质泥岩；再向下为油4#岩层。巷道所处地层埋深-620 m，竖向地应力10 MPa，水平向最大主应力14.5 MPa，最小主应力10 MPa，最大主应力方向与研究巷道轴向基本一致。

巷道为直墙半圆形断面，采用锚杆拱架联合支护形式，采用MSGLD-335/18×2250 螺纹钢锚杆，间排距 650 mm×800 mm；后喷射 120 mm 厚 C20 混凝土；最后架设U36 拱架，排距800 mm。巷道围岩变形仍然难以控制，拱腿出现弯折现象、屈服失效严重，锚杆破断现象频发。

2.2 试验方案

试验方案分3 组：第1 组为原支护方案，无锁拱锚杆；第2 组以锁拱点高度H（施加位置距巷底垂直高度）为变量；第3 组以锁拱锚杆长度L 为变量。数值模拟试验具体方案见表1。

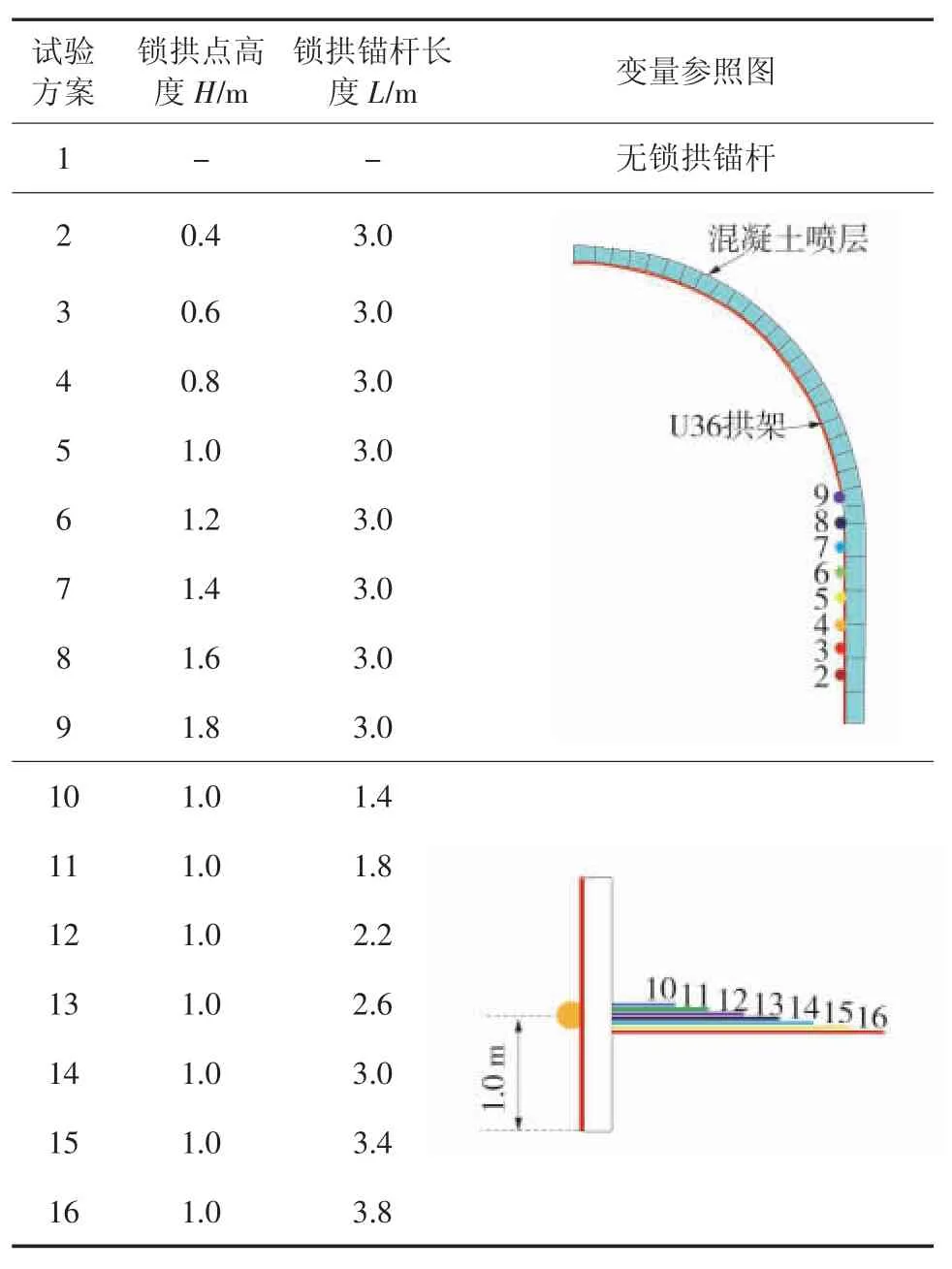
表1 数值模拟试验方案Table 1 Numerical simulation test scheme

2.3 试验模型及材料参数

结合实例，建立宽×高×厚为40 m× 40 m×0.8 m的模型，模型侧面约束法向位移，底面约束全位移，顶面施加面荷载进行应力补偿，模型及边界条件如图2，巷道全断面1 次开挖，然后进行混凝土喷层、锚杆和拱架的模拟。围岩采用SVISIC 蠕变模型，混凝土喷层选用Mohr-Coulomb 模型。断面及支护构件布置图如图3。岩层及喷层力学参数见表2。

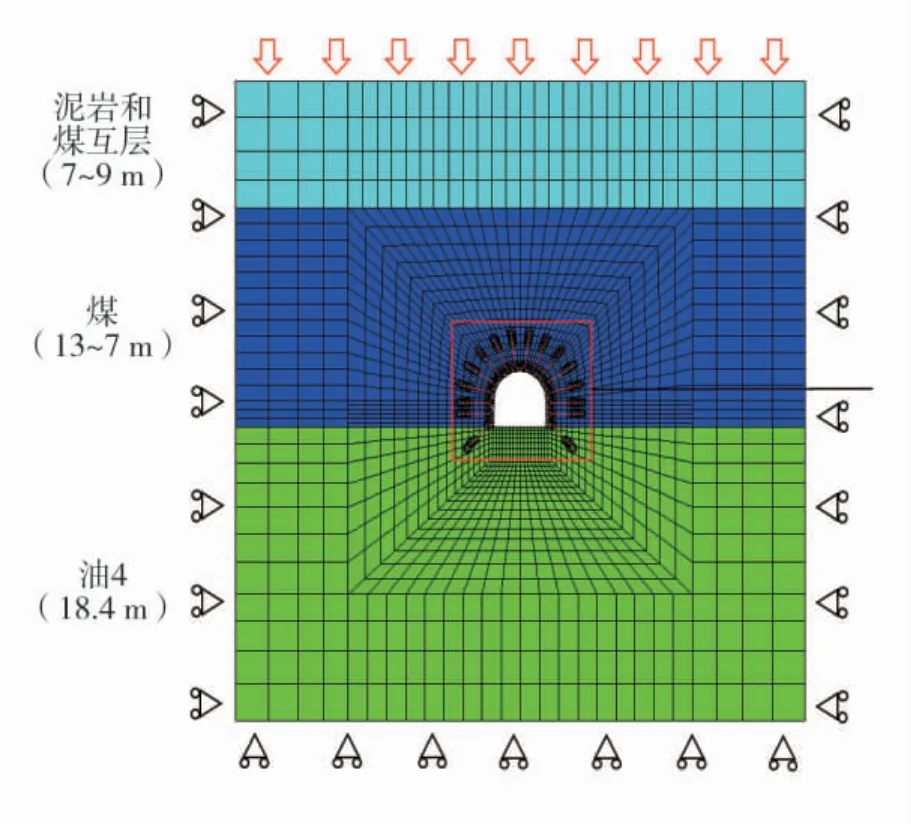
图2 数值计算模型示意图Fig.2 Numerical calculation model

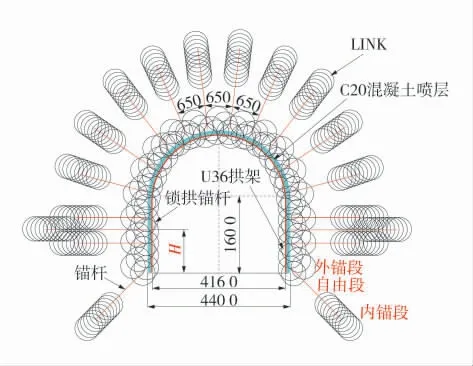
图3 断面及支护构件布置形式示意图Fig.3 Section and support member layout

锚杆（cable）单元布置在厚度方向中截面（0.4 m处）位置。常规锚杆按间距650 mm 布设，直径为18 mm，长度2.2 m，划分为22 个单元，其内锚段、自由段和外锚段长度分别为0.8、1.3、0.1 m，外锚段的端点与喷层的临空轮廓线平齐；锁拱锚杆根据各方案的具体要求进行建模，每个单元长度0.1 m，锚固段长度均为0.8 m，自由段外端点固定于拱架上；常规锚杆及锁拱锚杆力学参数见表3。

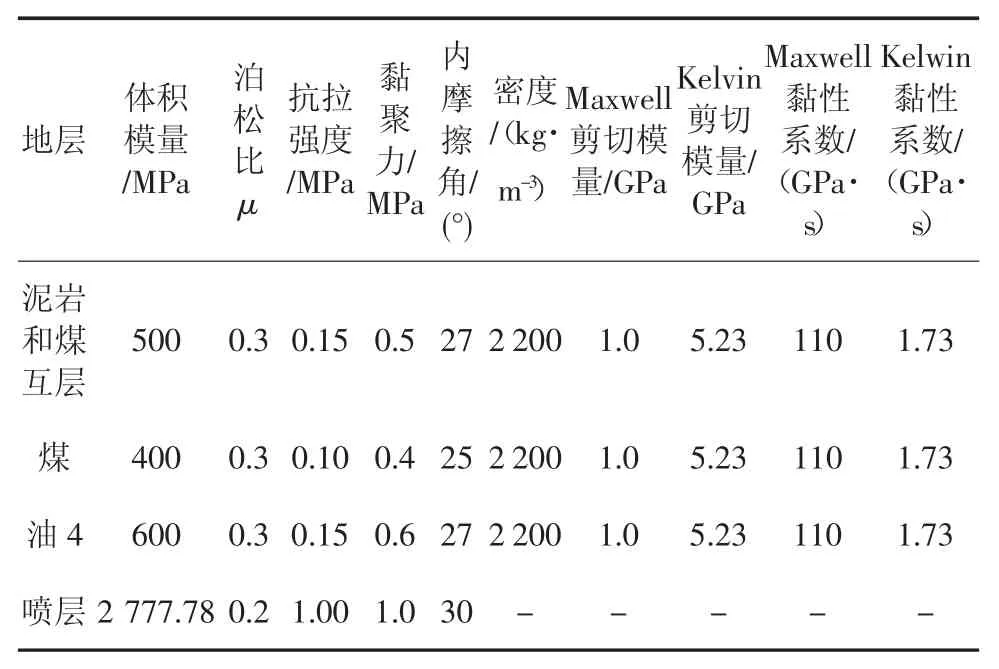
表2 岩层及喷层力学参数Table 2 Mechanical parameters of rock and jet formation

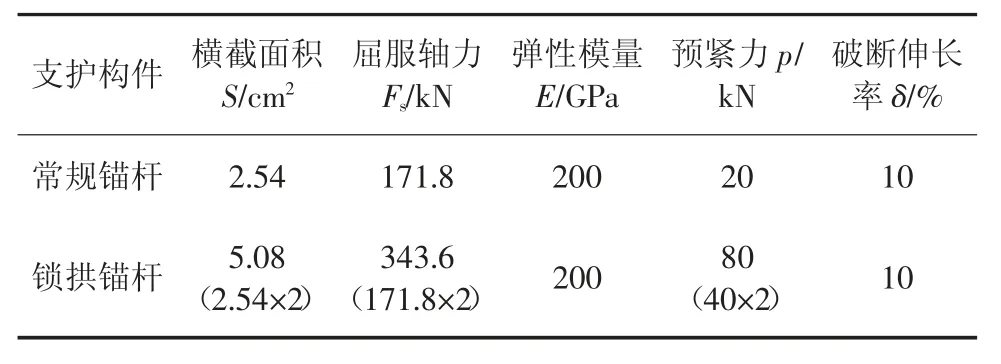
表3 常规锚杆、锁拱锚杆力学参数Table 3 Mechanical parameters of conventional bolt and arch locking bolt

进行锚杆模拟时，将自由段处锚固剂参数设置为0，并删除node 与围岩建立的link 连接；内锚段无需其他处理，外锚段处锚固剂参数设置为较大的数量级，以此模拟锚杆托盘。考虑到现场锚杆受到复杂的组合荷载作用，破断时的伸长小于其轴拉极限延伸率，因此将2 类锚杆自由段总体破断伸长率均设置为10%，如方案5 锁拱锚杆自由段极限长度S1max=（1+0.1）×2.1=2.31 m，常规锚杆自由段极限长度 S2max=（1+0.1）×1.3=1.43 m。

拱架模型共划分52 个beam 单元，2 个直腿处各有8 个单元，高度为1.6 m；半圆拱处共有36 个单元，半径为2.08 m。拱架采用U36 型钢拱架，将U36 型钢压弯组合判据m-n 公式写入主程序，并激活拱架-围岩相互作用模块，实现拱架与围岩的法向分离和轴向滑移。拱架截面几何参数为：①截面形式：U36；②横截面积：45.69 cm2；③惯性矩 Ix：9.29×10-6m4；④惯性矩 Iy：1.25×10-5m4；⑤弹性模量：206 GPa；⑥极限轴力：1 457.6 kN；⑦极限弯矩：48.30 kN·m。压弯破坏判据为[15]：

2.4 计算及监测

计算过程中对巷道变形量、塑性区体积、拱架支护反力、锚杆内力等进行监测，以蠕变时间达到50 d 为计算终止标准，部分计算结果统计见表4。

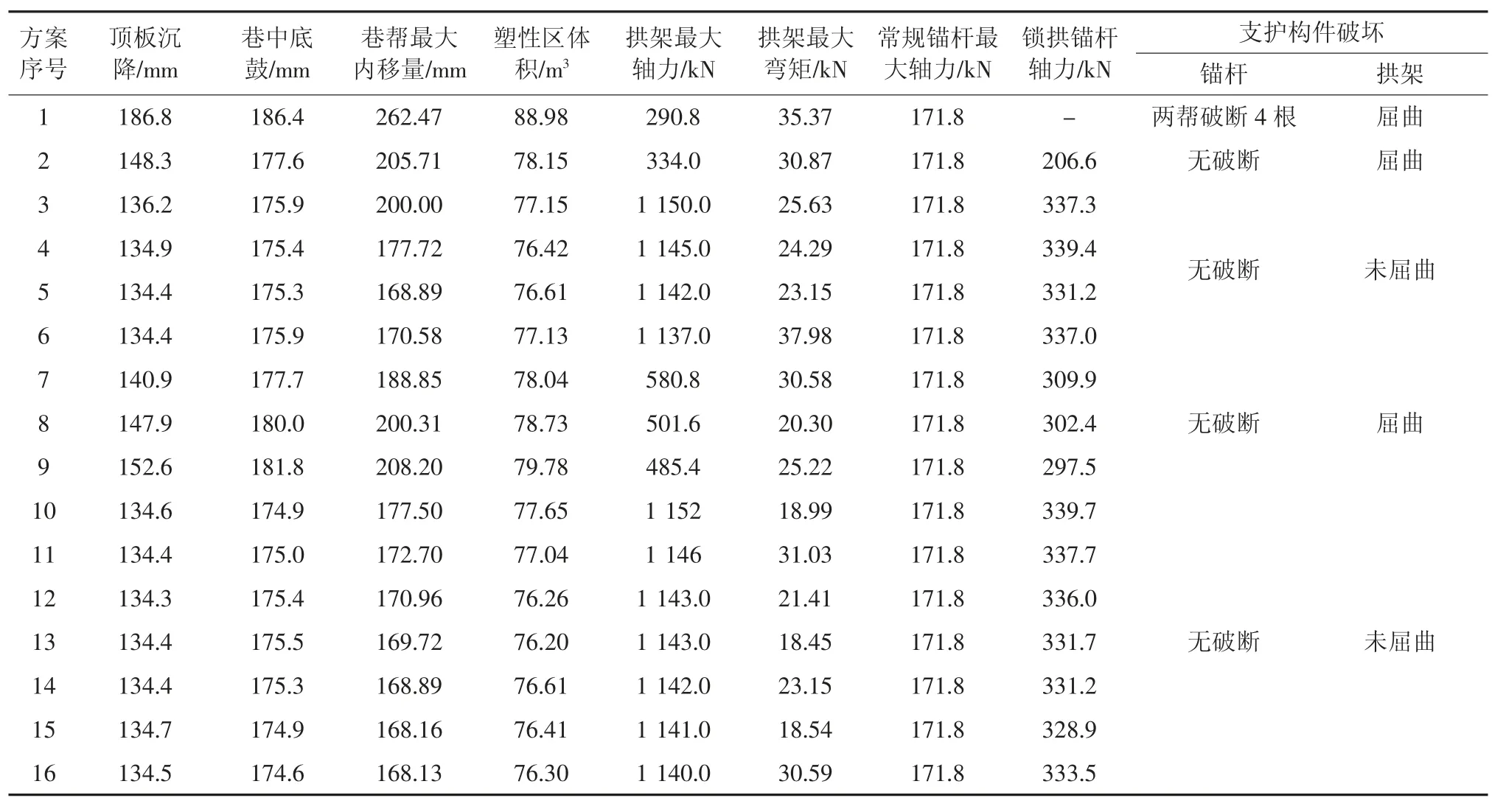
表4 部分计算结果（50 d）Table 4 Partial calculation results（50 d）

3 数值试验结果分析

3.1 锁拱锚杆效果分析

方案1（原支护）与方案5（H=1 m, L=3 m）的位移云图如图4，部分方案围岩变形、塑性区范围、拱架形态及锚杆轴力图如图5。

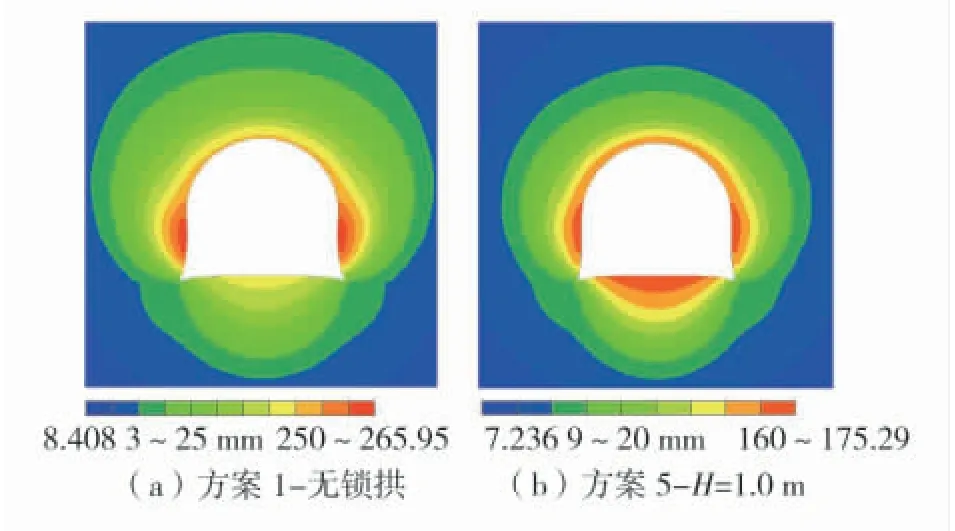
图4 方案1 与方案5 巷道围岩位移云图（50 d）Fig.4 Cloud diagrams of surrounding rock displacement of roadway in scheme 1 and scheme 5（50 d）

分析计算结果可知：

1）无锁拱锚杆情况下，围岩最大变形量达到了266 mm，如图4（a），塑性区深度达 4.5 m 以上，如图5（a），塑性破坏发展深入，围岩变形严重导致支护构件稳定性较差；计算至12 d 时，拱架拱腿率先发生曲折，轴力大幅下降，拱架-围岩逐渐分离；50 d 时拱架整体变形剧烈，如图5（a），拱架屈曲失稳，两帮锚杆破断4 根，支护构件已基本丧失承载能力，与现场情况基本一致。

2）锁拱方案效果明显改善，如采用高度1.0 m锁拱方案时，围岩最大变形量、起拱点内移量、塑性区范围比无锁拱锚杆支护方案对应值分别降低了34%、32.6%、23%，锚杆均未出现锚杆破断现象且拱架形态保持完好，拱架轴力较大且保持稳定，拱架未屈曲，锁拱锚杆作用体现较为明显。

对比分析可知，在无锁拱锚杆时，直墙半圆形巷道帮部产生内挤变形，使拱腿较早达到压弯极限，导致拱腿弯曲变形进一步发展，使拱架丧失承载能力；另一方面，围岩压力使拱腿的弯曲变形速度大于巷帮的内移速度，导致拱架与围岩分离，进一步使巷帮变形失控，进而导致整个巷道的变形破坏；此外，锚杆的破断失效也导致了围岩支护失效。

总之，拱腿部位的内弯变形和与围岩的脱离是拱架支护最终失效的突破口。而在锁拱锚杆方案中，锁拱锚杆有效控制了拱腿内弯变形且防止了拱架与围岩的脱离，保证了支护体系的完整性，最终支护效果明显改善。因此，对于锚杆拱架联合支护巷道，在关键部位安装锁拱锚杆是保障支护体系围岩控制能力持久有效的重要途径。

图5 部分方案围岩变形形态、塑性区范围、拱架形态及锚杆轴力（50 d）Fig.5 Part of the plan： surrounding rock deformation form,plastic zone range, arch form and axial force of anchor rod（50 d）

3.2 锁拱锚杆高度影响分析

方案1～方案9 巷帮最大内移量、塑性区体积、拱架与锁拱锚杆内力变化曲线如图6。其中，拱架最大轴力是指计算完成后拱架各截面受到的最大轴力。拱架拱腿中部单元（beam 单元编号356）轴力随时间变化曲线如图7。

分析图6、图7 可知：

1）当锁拱点高度由 0.4 m 逐步增大至 1.8 m（方案2～方案9）时，巷帮最大内移量呈先减小后增大的规律，在H=1.0 m 时下降至最低点，锁拱点位置影响显著；塑性区体积也先减小后增大，在锁拱点高度0.8 m（方案4）时最小，但在之后增幅较小，基本控制在80 m3以下。

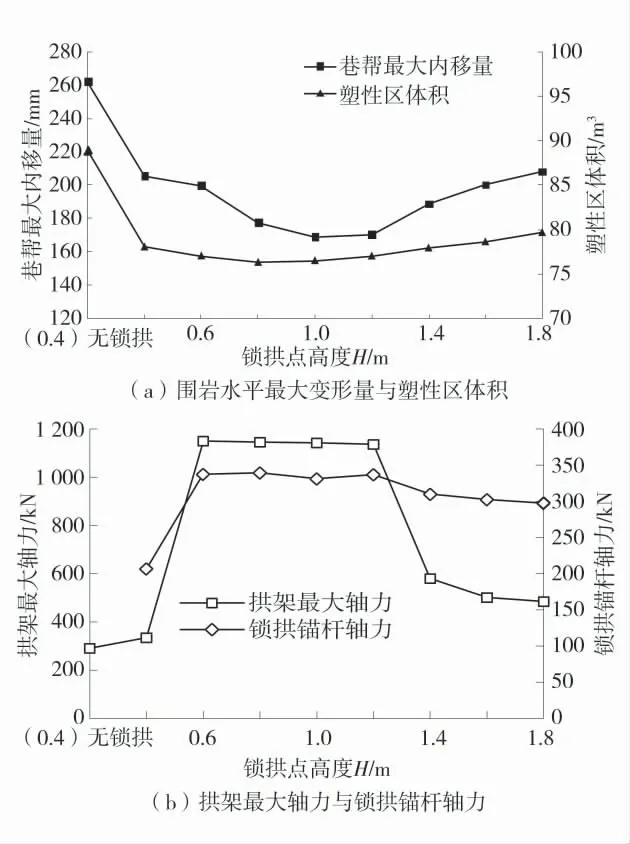
图6 方案1～方案9 围岩及支护构件响应指标变化曲线（50 d）Fig.6 Change curves of response indexes of surrounding rocks and support components for schemes 1-9（50 d）

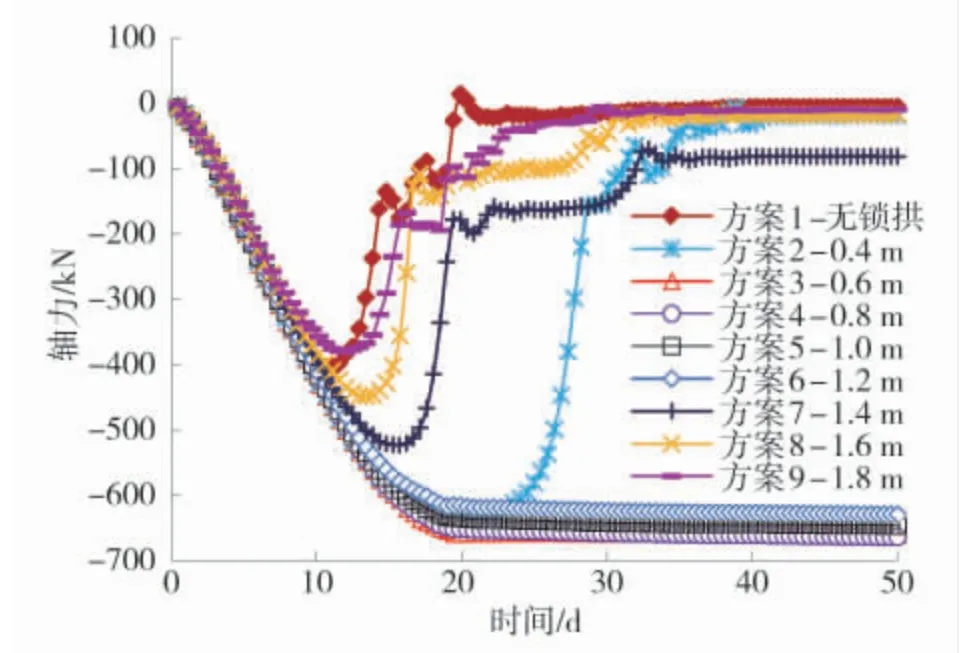
图7 方案1～方案9 拱腿轴力随时间变化曲线（轴力取自拱腿中点单元，编号356）Fig.7 Variation curves of axial force of the arch leg with time（axial force is taken from the mid-point unit of the arch leg, No.356）

2）锁拱高度0.4 m 时，锁拱点以上至起拱点位置拱腿曲折严重，拱架轴力出现大幅下降，拱架发生屈服；锁拱高度 0.6～1.2 m（方案 3～方案 6）时，支护构件受力变形程度基本一致：拱架最大轴力与锁拱锚杆轴力分别为1 140 kN 和330 kN 左右，已接近但未达到极限荷载，表明构件处于正常承载状态，拱架形态保持完好未发生屈曲，如图5（b）、5（c）。随着锁拱点位置继续提高，锁拱锚杆轴力出现明显下降，拱架拱腿部位再次出现弯折现象，最大轴力由1 137 kN 骤减至 580.8 kN，拱架屈曲，如图5（e）和 5（f）。

3）锁拱高度0.4 m 方案中，拱腿轴力初期直线上升，18 d 时达到峰值并保持稳定，而23 d 时轴力骤降，后保持在 0 值附近；锁拱高度 0.6～1.2 m 时，拱腿轴力在19 d 后基本保持在615～630 kN 的稳定状态；锁拱高度 1.4～1.8 m，拱腿轴力后期衰减并丧失的现象再次出现，而且衰减出现时间随锁拱高度增大而提前。

因此，锁拱点高度对于围岩变形及支护构件受力影响显著，存在最优锁拱高度。对于本工程实例，应该在拱腿中部或中部偏上为宜，以锁拱点高度1.0 m 为最佳方案。

3.3 锁拱锚杆长度影响分析

方案10 和方案14 围岩变形、塑性区范围、拱架形态及锚杆轴力图如图8；方案10～方案16 围岩水平最大变形量、塑性区体积、支护构件内力变化曲线图9。结合图8 和图9 分析可知：对比无锁拱锚杆支护方案，锁拱锚杆长度为 1.4～3.8 m 的所有方案中，锚杆无破断现象，拱架形态完好，支护效果均改善显著；增大锁拱锚杆长度，围岩变形量呈减小趋势，但减幅随锁拱锚杆长度的增加而减小，在长度3 m 后基本不再变化。塑性区体积受锁拱锚杆长度影响更小；拱架最大轴力与锁拱锚杆轴力均随锁拱锚杆长度的增加而减小，但并不显著。

从工程实践的层面来讲，虽然1.4 m 的短锚杆也能达到较好效果，但应考虑短锚杆现场锚固效果不佳；增加锁拱锚杆长度能够换来一定的巷道控制效果，但应考虑支护成本和施工难度因素。因此，锁拱锚杆长度应在综合考虑围岩控制效果、施工难度与经济成本等因素的条件下确定一个合理值。

基于上述数值试验结果，结合案例巷道的实际施工条件，确定了锁拱点高度为1.0 m、锁拱锚杆长度为3.0 m 的优化方案，并在进行了现场实施。监测表明该优化方案段的巷道，拱架未发生屈曲大变形，锚杆未发生破断，围岩控制效果明显优于原方案，锁拱锚杆使支护体系的整体支护能力得到提升。

4 结 论

1）锚杆-拱架联合支护数值模拟技术可实现锚杆杆体破断、拱架压弯屈曲、拱架-围岩相互作用的精细化模拟。

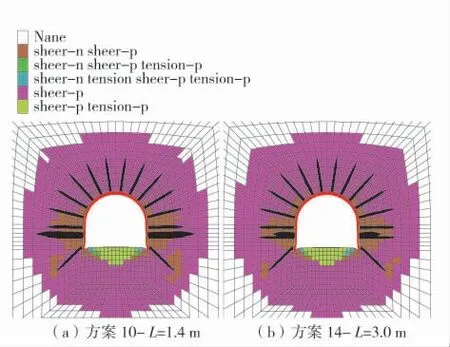
图8 方案10、方案14 围岩变形形态、塑性区范围、拱架形态及锚杆轴力（50 d）Fig.8 Surrounding rock deformation form, plastic zone range,arch form and axial force of rock bolt（50 d）

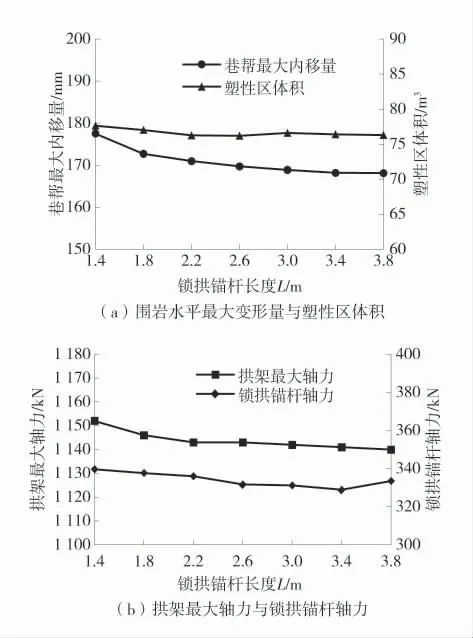
图9 方案10～方案16 围岩及支护构件响应指标变化曲线（50 d）Fig.9 Change curves of response indexes of surrounding rocks and support components for schemes 10 to 16（50 d）

2）无锁拱锚杆方案巷道中，拱架拱腿部位的内弯变形和与围岩的脱离是巷道最终变形失效的突破口；锁拱锚杆方案中，锁拱锚杆有效的控制了拱架拱腿的内弯变形且防止了拱架与围岩的脱离，保证了支护体系的完好性，最终支护效果明显改善，典型锁拱方案（H=1.0 m, L=3.0 m）围岩变形量降低了 34%。

3）锁拱点高度对于围岩变形及支护构件受力影响显著，巷道变形量随锁拱点高度（0.4～1.8 m）的增加呈先减小后增大的凹形曲线，存在最优锁拱高度；巷道变形量、塑性区体积和支护构件受力的等支护效果指标随锁拱锚杆长度L 的增大趋好但并不显著。

4）结合施工条件确定了锁拱点高度为1.0 m、锁拱锚杆长度为3.0 m 的优化设计方案，现场实践表明锁拱锚杆使支护体系的整体支护能力得到提升。