基于逆可靠度的单轨梁容许应力计算方法
王识嵎,梁 力
(1.华北水利水电大学土木与交通学院,郑州 450045; 2.东北大学资源与土木工程学院,沈阳 110819)
引言
长期以来,我国铁路桥梁设计一直采用容许应力法,通过安全系数K赋予结构充足的安全裕量,保证在各种荷载组合作用下能够维持其预定功能。而在公路桥梁设计领域,基于可靠度理论的第二套结构设计方法早已推广,将安全系数K写成分项系数的做法不仅提高了规范的适用性,而且赋予了极限状态方程以概率含义,使得设计者可以从失效概率层面控制结构的安全性能。
在铁路建设新形势下,基于结构力学-材料力学的容许应力法显然不利于材料的节约,而且缺少对结构安全裕度的科学解释[1-2]。中国铁路总公司已经出台《铁路桥涵极限状态设计暂行规定》(以下简称“极限状态铁标”)[3],可以预见在不久的将来,基于可靠度的概率极限状态设计法将获得更大应用空间。
现阶段公路桥梁设计大多参考GB 50153-2008《工程结构可靠性设计统一标准》(以下简称“国标”)[4]中关于目标可靠度的规定;而对于铁路桥梁来说,并没有一个足够权威的说法,规定中要求基于校准法通过参考规范中隐含的可靠度来确定各分项系数[5]。容许应力法中K的规定值往往较大,对应的可靠度也偏大,不适于单轨梁。“极限状态铁标”基于极限状态法确定了分项系数,为单轨梁的设计提供了目标可靠度指导。
逆可靠度分析是近年来兴起的一种逆向求解极限状态方程中未知量的新方法,当未知量为安全系数时,恰好克服了试错法求解可靠度庞杂的计算量。目前逆可靠度原理在桥梁工程中应用还很有限,大部分集中在稳定系数的求解[6],少数学者通过编程[7]、构造响应面[8]等方法实现逆可靠度分析,但都具有工作量大的问题。如何妥善地构造极限状态方程并求解未知量,是逆可靠度分析的关键。
提出一种基于函数拟合原理的逆可靠度分析方法,首先明确了不同恒活载比对可靠度的影响程度,随后取适当的荷载比并根据“极限状态铁标”中已知的混凝土构件受弯极限状态方程和分项系数计算了目标可靠度;接着,在目标可靠度基础上基于函数拟合原理反解安全系数,修正了GB 50458—2008《跨座式单轨交通设计规范》(以下简称“单轨规范”)[9]中各工况对应的应力提高系数;最后,讨论了不同参数的概率特征值对可靠度计算结果的影响,明确了各项参数对可靠度计算结果的控制程度,为单轨梁的设计提供指导。
1 逆可靠度理论
逆可靠度分析的核心在于极限状态方程的构建和其中未知量的求解,文献[10]将逆可靠度分析过程定义为如下规划问题

(1)
其中,βt为给定的目标可靠度,u为随机变量,θ为待求参数,G(u,θ)为极限状态方程。
对于式(1)一类规划问题,早期学者大多使用试错法进行求解,但主观随意性很大,效率往往较低。
实际上,根据逆可靠度的理念可将可靠度看作关于未知变量的函数。当未知变量为安全系数K时,式(1)规划问题可转化为
β(K)=βt
(2)
K反映了结构构件安全裕量的多少,显然,β(K)关于K连续且单调递增,某一确定的β有且仅有一个K与其对应,这满足反问题求解的适定性。
在未知β-K的关系时,将式(2)视为β-K平面上一条任意形状的曲线。根据函数拟合原理,可通过已知的样本点(Ki,βi)得到β(K)的拟合方程,再迭代求解βt对应的安全系数,当极限方程可靠度满足收敛要求即可。
需要指出的是,拟合函数次数越高所需的初始样本点越多,由此带来的可靠度正向分析的代价也越大。经大量试算,绝大多数工程结构的可靠度与安全系数近似满足二次函数关系,以二次函数作为拟合表达式求解目标可靠度能够满足精度要求。
2 “容许应力铁标”可靠度的校准
2.1 确立极限状态方程
传统铁路设计规范以安全系数K评价构件的安全性,其各项力学指标应满足式(3)要求。其中,对于预制混凝土构件来说,主力作用下K取值为2,SG和SQ分别表示恒载效应和活载效应,R表示对应的抗力。
K(SG+SQ)≤R
(3)
其中,材料抗力的不确定性受诸多因素影响,以km体现材料性能的不确定性,以kC体现计算模式的不确定性,以kG和kQ分别体现恒载效应和活载效应的不确定性,则式(3)对应的极限状态方程如式(4),随机系数的概率特性见表1。
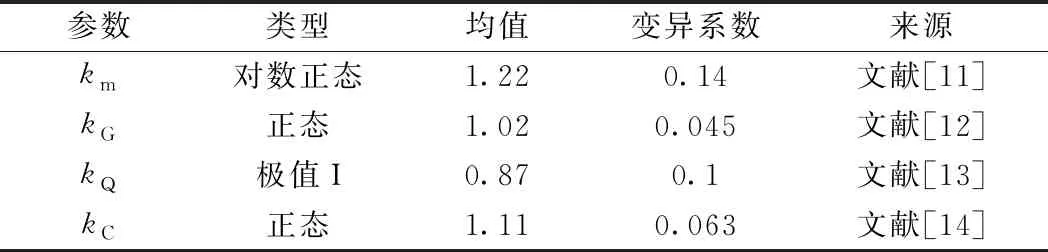
kCKkm(SG0+SQ0)-(kGSG0+kQSQ0)=0
注:活载效应中仅考虑占绝大部分的列车荷载。
2.2 可靠度的计算与比较
为便于说明,以0.1为步长,令SQ0和SG0的比值α为0.4~1.0,安全系数K值为1.5~2.2,对应的可靠度见图1。
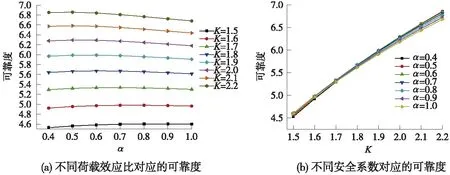
图1 “容许应力铁标”隐含的可靠度
由图1可知,随着活载效应占恒载效应的比例提高,同一安全系数下极限状态方程的可靠度下降趋势并不显著。当安全系数K=2.2时,β1.0-β0.4>0.2,证明活载效应的占比对基于容许应力法设计的铁路桥梁安全性能来说影响不大。这是因为容许应力法通过安全系数实现“一把抓”,设计结果对荷载的适应能力较强,结构的安全性也更易被工程师掌控。
另外,参考部分实际算例可知,铁路桥梁的活载效应占恒载效应的65%~85%,TB 10092—2017《铁路桥涵混凝土结构设计规范》[15](以下简称“容许应力铁标”)中关于安全系数的规定,铁路预制混凝土构件(K=2)对应的设计可靠度约为6.27,与国标中规定的目标可靠度βT=5.2存在较大出入。若以国标目标可靠度进行铁路桥梁设计,则有可能导致铁路桥安全度不满足正常运营需求,甚至酿成惨痛工程事故。
3 “极限状态铁标”可靠度的校准
相比于公路规范来说,容许应力铁路规范的安全系数提供给结构的安全度更大,但是以这样的安全度进行设计可能存在浪费,尤其是对于以客运为主的城轨桥梁来说更不适用。
“极限状态铁标”基于概率极限状态法制定,恰好为校准单轨梁的设计目标可靠度提供了契机。通过参考极限状态方程隐含的可靠度,校准单轨设计目标可靠度,使得结构安全度处于合理水平,进而实现改进单轨规范的目的。
3.1 可靠度的计算
“极限状态铁标”中以分项系数的形式对结构设计的安全性进行了规定,对于受弯构件来说,在承载能力极限状态下的基本组合I(主力组合)对应的极限状态方程为R′-(SG1+SG2+SQ)=0,其中SG1,SG2分别为一期恒载效应和二期恒载效应的标准值,SQ为活荷载效应标准值,R′为抗力设计值,根据分项系数的要求,R′必须大于γm(1.2SG1+1.4SG2+1.4SQ)。
以0.1为步长,令二期恒载与一期恒载的比值θ为0.7~1.2,活载效应与恒载效应的比值α为0.4~1.0计算式(5)的可靠度。其中γ0为结构重要性系数,γm为材料分项系数,kG1和kG2分别为一期恒载和二期恒载不确定性系数,其他参数的含义同式(4)。约去公因子SG10后求解可靠度,见图2。
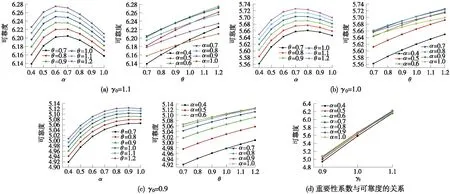
图2 铁路极限状态规范的隐含可靠度
γ0kCkRγm×(1.2kG1SG10+1.4kG2θSG10+
1.4×0.7kQ(SG10+θSG10))-kG1SG10-
kG2θSG10-0.7kQ(SG10+θSG10)=0
(5)
3.2 可靠度的校核
由图2可知,对某一确定的γ0来说,式(5)隐含的目标可靠度随α值的不同先升后降,存在一个最优的活载占比,使得设计目标可靠度达到最高。这意味着使用极限状态法进行铁路桥梁设计时,可以通过调节荷载效应的占比优化设计可靠度。当γ0=1.1时,α≈0.7;当γ0=1.0时,α≈0.75;当γ0=0.9时,α≈0.9,基本与传统铁路荷载效应占比相一致。容许应力法通过安全系数K实现“一把抓”,设计者们往往不能反推各项荷载效应的控制作用,给规范优化制造了困难。再者,铁路桥跨径越大,受到恒载效应的制约就越明显,活载效应的占比也越小。因此,当γ0=0.9时,最优活载占比约为0.9,大于γ0=1.1时的最优活载占比,印证了极限状态规范的科学性。其次,当活载占比固定时,设计可靠度将随二期恒载占比的增加而增加,但增加幅度有限,最大值<0.1,这主要是因为二期恒载的组合系数高于一期恒载的组合系数,由二期恒载控制设计更加安全,因此设计时可以考虑适当提高二期恒载占比。最后,由图2(d)可知,在不同活载占比的情况下,可靠度随重要性系数增长近似呈线性增长的态势,且重要性系数γ0越高,荷载占比对可靠度的影响越小,可见极限状态铁标中等差重要性系数的确定是有科学依据的。
铁路活载与恒载效应的比值一般在0.7左右,二期恒载效应与一期恒载效应的比值在0.8左右,因此可以推定,当重要性系数γ0=1.1时,目标可靠度约为6.22;当重要性系数γ0=1.0时,目标可靠度约为5.67;当重要性系数γ0=0.9时,目标可靠度约为5.06。除三级结构的可靠度稍小,其余结构的可靠度均大于国标中规定的目标可靠度,对应的失效概率也远高于前述风险基线,这充分体现了铁路桥涵结构的特殊性和重要性[16]。另外,与容许应力铁标可靠度比对,发现重要性为一级的结构目标可靠度与旧铁标近乎一致,验证了铁路规范中的目标可靠度确实是经过校准法得来的,在制定跨座式单轨梁的设计规范时,有必要在参考铁标中目标可靠度的基础上做出适当调整。

表2 铁路桥涵结构安全等级划分标准
4 修正容许应力提高系数
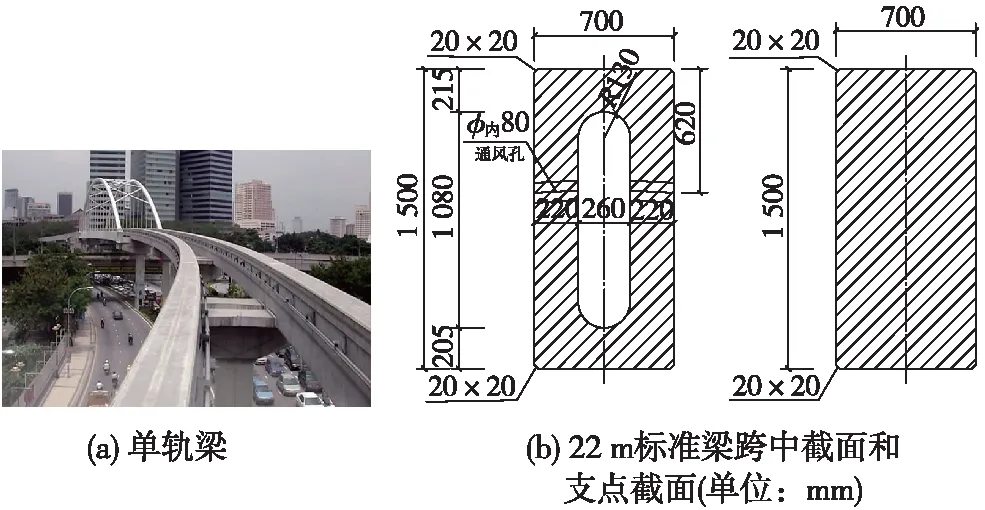
图3 单轨梁及其标准截面
跨座式单轨梁(图3)的走行机理、轮轨关系与地铁、普通轻轨都有很大区别,其梁体不仅起到承重作用,而且直接支承、导向列车,另外还是列车供电线路的载体,因此必须保证足够的安全性[17]。单轨规范沿袭了传统铁路规范的容许应力,并在此基础上乘以一定的提高系数,这是因为单轨交通和铁路交通存在差异,所需安全度较低,基于铁标可靠度进行设计可能存在浪费。
显然,容许应力提高系数的制定缺乏确凿的可靠度依据。而“极限状态铁标”是基于概率极限状态法编制的,恰好为单轨规范提供了逆可靠度分析所需的目标可靠度。
4.1 求解效率的比较
基于函数拟合的思想,分别使用一次、二次、三次多项式拟合β(K)曲线,考虑到工程精度需求和求解代价,取|β(K)-βt|<0.005作为收敛准则。
为了与斜拉索极限状态方程的形式相适应,假设某个极限状态方程为
G=2x1-μ(1.5x2+0.5x3+x4)
(6)
其中,xi为服从一定概率分布的变量,μ为待求未知量(相当于K)。令xi服从不同分布,初始点分别对应图4中A、B和C曲线。案例分布类型和分布参数见表3。

表3 案例分布类型和分布参数

注:A曲线xi对应表3分布类型,B曲线xi全部服从正态分布,C曲线xi全部服从极值Ⅰ型分布;均值和标准差均与表3相同图4 案例初始点
比较不同方法的求解效率时,由于A、B曲线差异甚微,故仅讨论对A、C曲线使用不同方法的求解效率。令βt分别等于0和1.5,反解μ的效率见表4。

表4 求解效率对比
对于A曲线来说,在整个β-μ平面内曲率很小,因此βt无论是等于0还是1.5时,求解未知系数μ所需的迭代次数较少;而对于C曲线来说,其曲率明显大于A曲线,意味着C曲线对应的极限状态方程更加复杂,因此逆解可靠度的效率有所增加,但总体上看仍然高于盲目试错。另外,大多数结构构件的安全系数的关系并不复杂[18],在考虑计算成本的前提下,建议使用抛物线拟合法作为逆可靠度分析方法,后文计算在未做特别说明的情况下均按此进行。
4.2 可靠度计算
“单轨规范”中不同荷载组合对应的容许应力提高系数φ不同,以组合1(恒载+列车竖向静活载+列车竖向动力作用)为例,其极限状态方程
kCKkR(SG0+SQ0)-φ(kGSG0+kQSQ0)=0
(7)
其中φ按规范取1,其他参数的含义同式(4)。由于单轨梁从工厂预制,二期恒载较小,加之列车编组比较固定,因此不同项目的荷载特性差别不大。以深圳坪山云轨项目22 m简支梁为例,其列车荷载效应约为恒载效应的1.6倍。以0.1为步长,令列车荷载效应与恒载效应的比α为1.3~2.0,安全系数K取为1.5~2.0,遍历所有K-α的组合,计算式(5)的可靠度如图5所示。
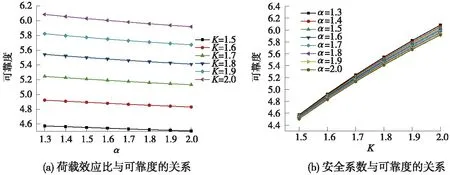
图5 “单轨规范”隐含的可靠度
由于单轨梁活载效应占比偏高,其K-α-β曲线与传统铁路梁并不一致。当活载占比逐渐增大时,可靠度下降的趋势偏于平缓,这意味着活载效应对可靠度的影响也是有限的。当K=2,α=1.6时,单轨设计可靠度约为6.00,相比于“极限状态铁标”中一级结构的可靠度偏低,但是高于二级结构的可靠度5.67。结合表2中的铁路桥涵安全等级的划分标准来看,单轨梁的实际安全等级宜取为二级,因此单轨规范的安全度还是偏高,应力提高系数存在进一步的优化空间。
参考“极限状态铁标”中的目标可靠度和可靠度国标中的相关规定,则单轨梁的设计目标可靠度宜取为βT1=5.7,βT2=5.2(与一级脆性破坏可靠度相一致)。T1和T2分别为两种不同的安全等级,对应着铁路桥涵的二级和三级结构,其可靠度大小相差为0.5,满足Q/CR 9007—2014《铁路工程结构可靠性设计统一标准》[19]中第3.2.7条规定(上下两级目标可靠度宜相差0.5)。
4.3 容许应力提高系数的修正
为修正容许应力提高系数,将式(7)中的容许应力提高系数φ视为未知量,以0.05为步长,分别令φ=1.05~1.2,则式(7)对应的可靠度如图6所示。
将可靠度视为应力提高系数φ的函数,以α=1.6为例,根据函数拟合原理,取(1,6.003 7),(1.1,5.531 4)和(1.2,5.091 2)为样本点,将可靠度写成应力提高系数的函数如式(7)。
β=1.74φ2-8.58φ+13.154
(7)

注:活恒载效应之比α取为1.5~1.7,安全系数取为2图6 应力提高系数与可靠度的关系
按上节所述,取目标可靠度βT分别为5.7和5.2,解得对应的容许应力提高系数φ5.7=1.063,φ5.2=1.175,分别对应铁路桥涵极限状态规范中的二级和三级。结合单轨规范中关于应力提高系数的规定来看,其优化的空间不大,这也从侧面印证了单轨规范的科学性。
同理,对α=1.5和α=1.7的情况进行逆可靠度求解,解得应力提高系数汇总如表5所示。可见,随着活载效应占比的减少,容许应力提高系数稍许增加,但总体上处于较低水平,可以考虑将荷载组合1下(K=2)单轨梁的容许应力提高系数定为1.05。

表5 不同活恒载效应比下的应力提高系数
4.4 不确定性系数的讨论
尽管对应力提高系数进行了调整,但显然单轨梁的荷载特性与铁路梁存在区别,导致km、kG、kQ和kC与铁路梁存在差异,有必要探究参数的概率特征对可靠度计算结果的影响。
以主力组合为例,安全系数K取为2,容许应力提高系数取为1,保持km、kG、kQ和kC的分布类型不变,以0.05为步长,令km均值等于1.15~1.35,kG均值等于0.95~1.15,kQ均值等于0.75~0.95,kC均值等于1.00~1.20,可得式(7)对应的可靠度如图7所示。
(1)均值
由图7可知,km、kC对可靠度的计算结果影响较大,kQ对可靠度的影响次之,kG对可靠度的影响较小。容许应力规范以材料力学为理论基础,抗力的计算过程显著受到抗力的影响,因此在设计施工中必须保证质量满足规范要求,避免大幅度降低结构可靠度;随着活载均值的提高,可靠度下降的趋势较为稳定,但由于活载分布类型与恒载不同,其对于可靠度计算结果的影响也比较大,必须将其荷载效应控制在一定范围之内;恒载效应均值增加20%,对应的可靠度降幅不超过0.3,证明恒载效应不是控制单轨梁设计的主要因素。

图7 不确定性系数均值与可靠度的关系曲线
(2)变异系数
保持km,kG,kQ和kC的均值、分布类型不变,以0.02为步长,令km的变异系数为0.1~0.18,kG的变异系数为0.01~0.09,kQ的变异系数为0.06~0.14,kC的变异系数为0.02~0.10计算可靠度,结果如图8所示。
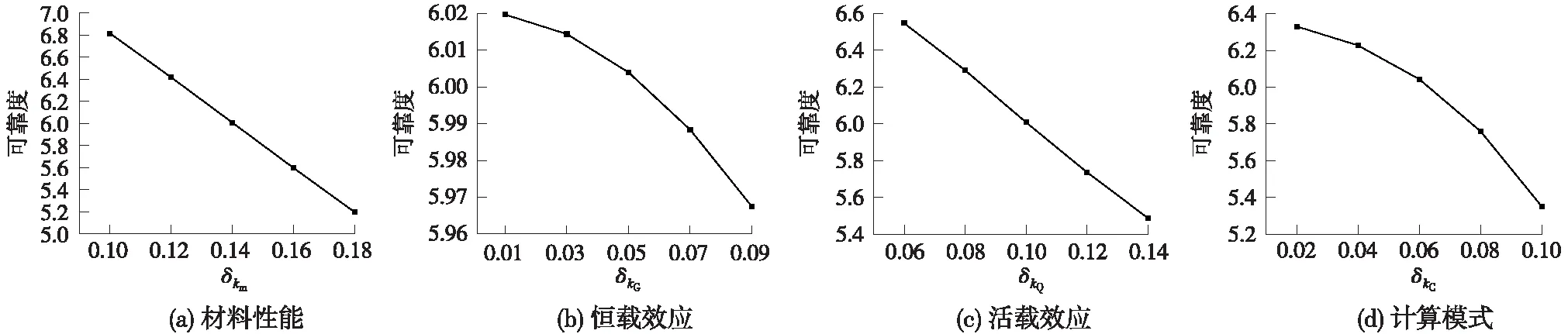
图8 不确定性系数变异系数与可靠度的关系
由图8可知,随着km,kG,kQ,kC变异系数的增大,可靠度呈下降趋势。其中,km的变异系数对可靠度的计算结果影响最大,随着km等差增加,可靠度也近似地呈现出等差下降的趋势。变异系数每增加0.02,可靠度下降约0.5,可见抗力的变异性对于结构的可靠性具有至关重要的影响;kQ的变异系数对可靠度计算结果的影响稍逊,随着kQ等差增加,可靠度有趋于平缓的下降趋势,但变异系数每增加0.02,可靠度约下降0.4,可见活载效应的变异性也是不能忽略的,有必要针对单轨梁列车荷载效应的特性展开研究;kC的变异系数对可靠度的影响次之,随着kC变异系数的增加,可靠度呈加速下降的趋势;kG的变异系数对可靠度的计算结果影响最小,当变异系数从0.01增长至0.09时,可靠度下降约0.05,说明恒载效应的变异性对可靠度的影响程度较小,加之单轨梁往往在工厂中预制,质量控制较好[20],恒载效应的变异性几乎不控制设计。
5 结论
提出一种基于逆可靠度原理的安全系数计算方法,通过校核铁路新旧规范,为跨座式单轨梁的设计提供了目标可靠度,并在此基础上完成了单轨梁容许应力提高系数的修正,主要结论如下。
(1) 铁路容许应力规范的可靠度高于可靠度国标的规定,当活载效应与恒载效应的比值约为70%时,预制混凝土构件在主力组合下的抗弯设计可靠度约为6.27。
(2) 使用铁路极限状态规范进行设计时,可以通过调节活载效应占比提高设计可靠度:当γ0=1.1时,α≈0.7;当γ0=1.0时,α≈0.75;当γ0=0.9时,α≈0.9。此外,二期恒载与一期恒载的比值对可靠度影响不大。
(3) 铁路极限状态规范基本沿袭了铁路容许应力规范中关于目标可靠度的规定,一级构件的可靠度约为6.22,二级构件的可靠度约为5.67,三级构件的可靠度约为5.06。
(4) 跨座式单轨规范仍然沿用了容许应力法的形式,只不过是通过容许应力提高系数考虑了与传统铁路桥涵的安全度差异。若以“极限状态铁标”中二级(取为5.7)、三级(取为5.2)可靠度为目标,则单轨规范中主力组合的容许应力提高系数可以分别提升至1.05和1.17。
(5) 抗力、列车活载效应和计算模式的概率特征参数对可靠度计算结果影响较大,在设计、施工过程中注意控制工程质量,加强对单轨梁活荷载概率特征的统计。

