基于多质点模型的高速列车速度控制研究
侯涛,郭洋洋,陈昱,杨宏阔
基于多质点模型的高速列车速度控制研究
侯涛,郭洋洋,陈昱,杨宏阔
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
在对高速列车速度控制的研究中,传统的单质点列车模型因未考虑车长及车间影响力,导致列车在经过特殊线路时速度会跳变,造成较大的速度控制误差。针对上述问题,在列车建模时考虑列车长度以及对每节车厢的受力进行深入地分析,在此基础上建立高速列车的多质点模型,并对其设计相应的模糊预测控制器进行列车速度跟踪控制研究。研究结果表明:对列车建立的多质点模型,能有效地解决列车在经过变坡点和变曲率点时产生的速度跳变问题,减小速度控制误差,且针对该列车模型设计的模糊预测控制器能很好的控制列车跟踪理想速度曲线运行,提高列车速度控制精度和舒适度。
高速列车;多质点模型;模糊预测控制;速度控制;动态矩阵控制

在高速列车中涉及到的技术体现的是轨道交通中顶尖的科学技术,它承担着国家的重大发展战略。高速铁路是通过大幅度地提高列车运行速度来实现高效运行,因而深受人们的欢迎。列车提速的关键是在能满足安全、可靠、高效运行的前提下,对其牵引力或制动力进行实时地调整。然而,不断提速的同时也要求对高速列车运行控制的响应更快、精度更高,因此,应对列车建立精确的动力学模型并且设计高性能的速度控制器来满足列车提速的需求。在传统的列车速度控制研究中将整个列车简化为一个质点,把列车上所有的受力都集中在一个点上进行分析。这种方法虽简单,但高速列车在运行过程中每节车厢所分配的牵引力或制动力不同,且各车厢的受力因所处的线路状况不同也各不相同,若将所有车厢简化为一个点进行分析,与列车实际运行情况相差较大,会造成较大的速度控制误差。而列车的多质点模型是将每节车厢都看作一个质点,对每个车厢的受力都进行分析,并且该模型考虑了列车的长度,弥补了单质点列车的不足。YANG等[1]分析了列车相邻的2个车厢间的耦合方式,建立了简单的高速列车多质点模型,并针对该模型设计了相应的巡航控制器,改善了列车巡航时的控制性能。LIN等[2]分析了相邻车厢间的耦合力是一种非线性力,针对列车巡航过程设计了一种滑模控制器,提升了列车运行的安全性。何晓琼等[3]研究了高速列车各个车厢应分配制动力的情况,进而建立了列车的多质点制动模型。SONG 等[4−5]将两车厢间的耦合力看作列车自身的内力,提出了一种“多质点−单位移”列车模型,简化了列车内部的受力情况。ZHANG等[6−8]针对多质点模型的重载列车,设计了速度预测控制器,优化了列车运行时的各项性能。高速列车在运行时,不同时刻分配给车厢的牵引力或制动力各不相同,不同车厢之间分配的牵引力或制动力也不同,因此建立列车的多质点模型更符合列车运行的实际情况。目前,我国高速列车主要采用传统的PID速度控制器,但PID控制更适用于线性系统。因此将PID控制应用于多质点模型的高速列车会造成较大的控制误差[9]。预测控制比较适用于复杂的控制过程,它能够通过预测未来的输出速度来调整当前的控制量,进而减小速度控制误差,提高控制精度。陈小强 等[10]把预测控制的优点加入到模糊PID控制中,设计了适用于单质点模型高速列车的预测模糊自适应PID控制器,减小了列车的速度跟踪误差。YANG等[11]针对动力集中型列车非线性的特点,设计了一种广义预测控制器,有效地减小了列车运行的速度和位移控制误差。Aradi等[12]将预测控制应用到了列车自动驾驶系统中,使列车在准时性和舒适性方面有了很大的提高。李中奇等[13]设计了单质点高速列车模型的双自适应广义预测控制器,在列车运行时同时修改模型参数和控制器参数,使列车在启动阶段和制动阶段的控制效果有了很大的改善。孟建军等[14]针对单质点模型的城轨列车设计了预测模糊PID控制器,较大程度的提高了列车的停车精度。杨辉等[15]针对高速列车的Elman模型设计了一种改进型的广义预测控制器,提高了列车的速度控制精度,使列车安全、准点地运行。针对一些复杂的控制过程,预测控制有很大的优势,因此本文将预测控制的优势加入到模糊控制中,设计了一种适用于多质点模型高速列车的模糊预测控制器,提高了列车速度控制精度及舒适度。
1 列车动力学模型
CRH3型动车组由4辆动车和4辆拖车组成,其中第1,3,6和8节车厢为动车,第2,4,5和7节车厢为拖车。
1.1 列车牵引特性
牵引特性是指列车在运行时该分配的牵引力和列车速度之间的关系。在列车启动时要求分配最大的牵引力来克服启动阻力,而在列车运行过程中该分配列车的牵引力大小则随着速度的增大而减小。CRH3型动车组的牵引特性公式如式(1)所示。
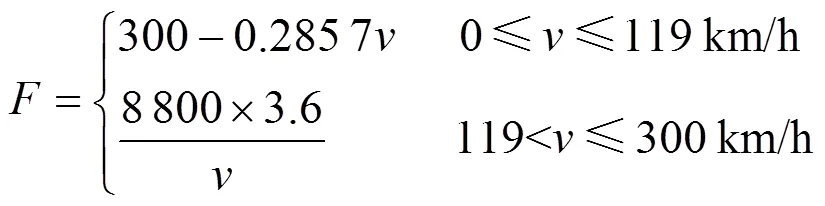
1.2 列车制动特性
与列车牵引特性类似,CRH3型动车组的制动特性如式(2)所示。
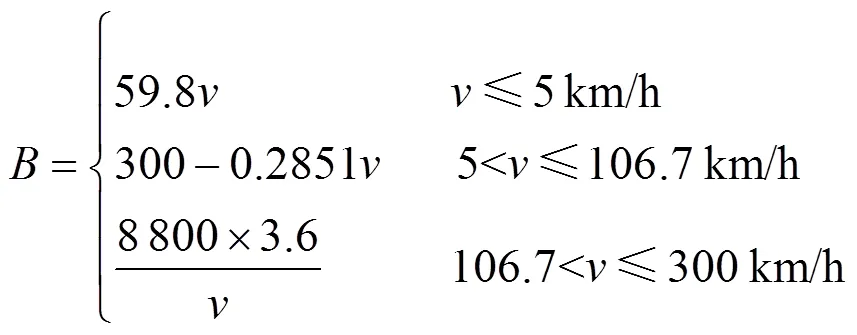
1.3 列车阻力
1.3.1 基本阻力
列车在任何运行状况下都会存在基本阻力(如空气阻力)。高速列车所受的基本阻力如式(3)所示。
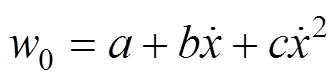
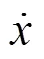
1.3.2 附加阻力
附加阻力是只有当列车运行在一些特殊的线路上(如弯道、坡道等)时,额外受到的一部分阻力。主要包括以下3种:
1) 坡道附加阻力
多质点模型的高速列车在通过坡道时的车厢分布示意图如图1所示。则列车在该坡上所受的单位坡道附加阻力如式(4)所示。
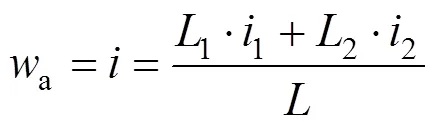
式中:wa为单位隧道附加空气阻力,N/kN;i1和i2分别为列车在第1和2坡段运行时的坡度;L为列车总长;L1和L2分别为列车在第1和2坡段上的长度,m。
2) 曲线附加阻力
高速列车在弯道上运行时所受的单位曲线附加阻力如式(5)所示。

式中:w为单位曲线附加阻力,N/kN;1和2分别为列车运行的第1和2曲线段上的半径,m;1和2分别为列车在第1和2曲线段上的长度,m;为常数,一般取600。
3) 隧道附加空气阻力
在高速列车通过隧道时会有一部分额外增加的空气阻力,这部分阻力则被称为隧道附加空气阻力。列车在隧道运行时所受的单位隧道附加空气阻力如式(6)所示。

式中:r为单位隧道附加空气阻力,N/kN;s为隧道长度,m。
综合以上各种阻力,则可得高速列车在运行时所受的总单位阻力如下:
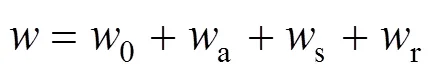
1.4 耦合力
将高速列车每个车厢看作一个质点进行分析时,还需考虑车厢之间的相互影响力,即耦合力。可将高速列车车厢间的耦合关系简化为一个“弹性−阻尼”系统,如图2所示,其数学方程如式(8) 所示。
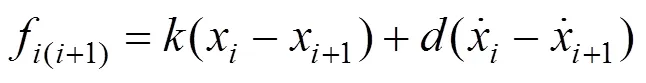
式中:为第i节车厢与第i+1节车厢之间的耦合力,N;与分别为第i节车厢与第i+1节车厢的位置,m;与分别为第i节车厢与第i+1节车厢的速度,m/s;k为车钩系统的弹性耦合系数,N/m;d为车钩系统的阻尼耦合系数,(N·s)/m。
综上所述,多质点模型高速列车的动力学方程如式(9)所示。
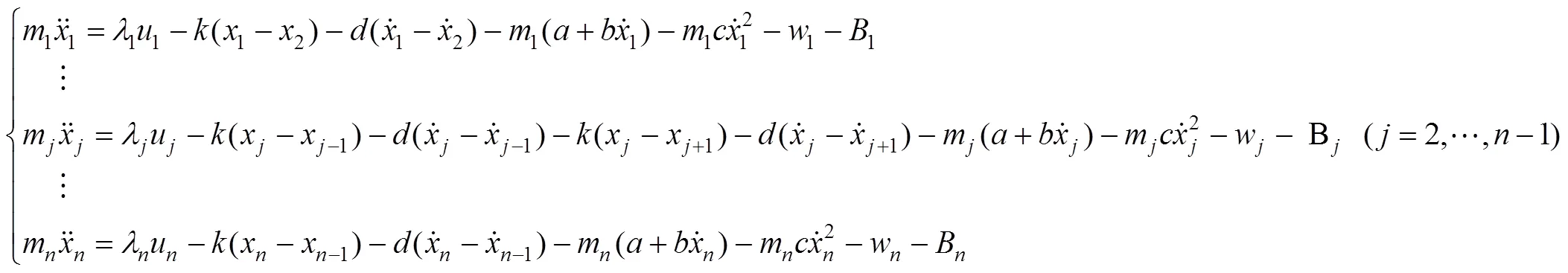
假设列车在运行时所受的空气阻力全部集中在车头上,则多质点模型的高速列车动力学方程如式(10)所示。

2 模糊预测控制器设计
在模糊预测控制器的设计中,选用模糊控制来控制列车运行速度,而用预测控制来预测下一时刻的列车速度,根据预测的速度来调整当前时刻对列车的控制量,从而减小速度跟踪误差。图3为模糊预测控制系统的结构。

图3 模糊预测控制系统的结构
由图4可以看出,为模糊控制器的输出,它的作用是控制列车速度。m为通过预测模型得到的+1时刻的预测速度值。将该速度预测值和列车在+1时刻的运行速度反馈到反馈校正环节,则能得到校正后的预测速度p。
2.1 模糊控制
模糊控制器的输入为目标速度r与校正后的预测速度p的误差及该误差的变化率e,输出则为对列车的控制量。表1为输出的模糊控制规则。
2.2 预测控制
2.2.1 预测模型
在时刻对高速列车施加一个控制增量∆(),得到在该控制作用下未来时刻的个预测速度值如式(11)所示。
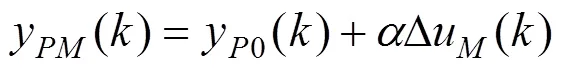
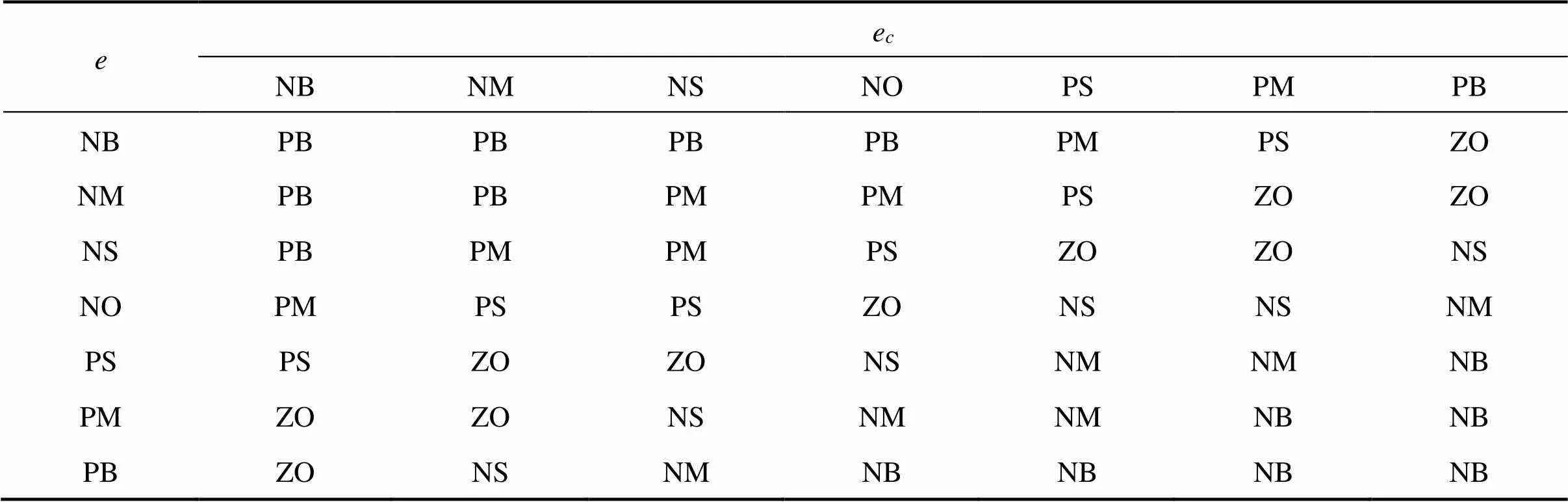
表1 输出u的模糊控制规则
2.2.2 反馈校正
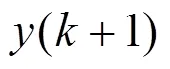
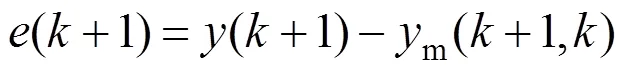
则校正后的预测速度如式(13)所示。
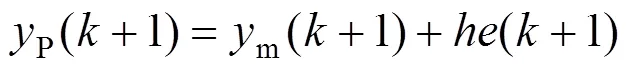
式中:为校正向量。
3 系统仿真及结果分析
3.1 系统仿真
3.1.1 列车模型设计
本文在列车建模中,选用CRH3型动车组的参数建立高速列车的多质点模型。图4为第1节动车车厢的仿真模型。其他7节车厢除基本参数和受力大小不同外,结构类似。
3.1.2 理想曲线设计
图5为本文设计的列车运行理想速度−时间曲线,开始时列车加速启动,当速度达到80 m/s后列车匀速运行,接近停车位置后减速直至停车。
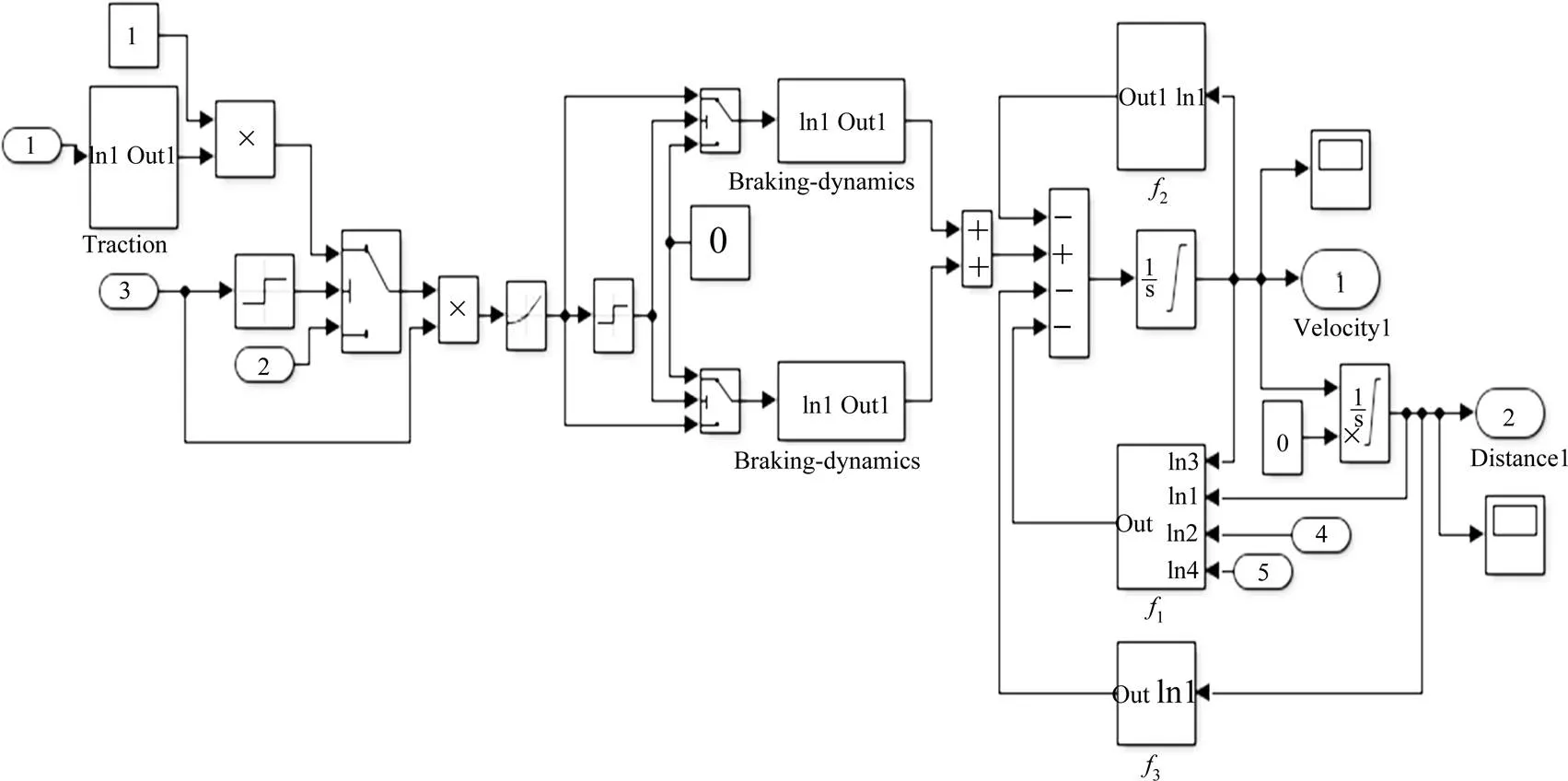
图4 高速列车第1节车厢仿真模型

图5 理想速度-时间曲线
3.1.3 仿真模型设计
图6为高速列车速度控制系统Simulink仿真模型。DMC是一种基于对象阶跃响应的预测控制算法,它直接以对象的阶跃响应离散系数为模型,给上述高速列车模型加一阶跃响应,结果为在50 s时系统基本达到稳定。为使模型参数α(=1,…,)尽可能完整的包含对象的动态信息则需在=时对象进入阶跃响应稳态,同时采样周期也应满足香农定理,因此对模型的各项参数取值分别为:=1 s,=50,=2和=16。
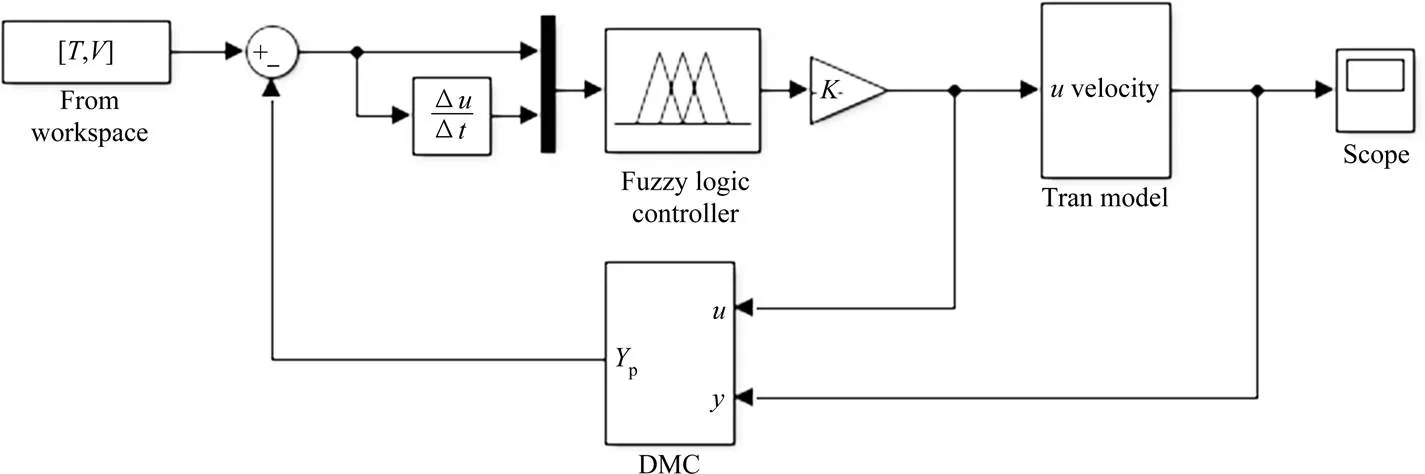
图6 高速列车速度控制系统仿真模型
3.2 仿真结果
对多质点模型的高速列车,用模糊控制器控制其速度,以前4节车厢为例,得到的仿真结果如图7所示,速度跟踪误差如图8所示,加速度变化曲线如图9所示。
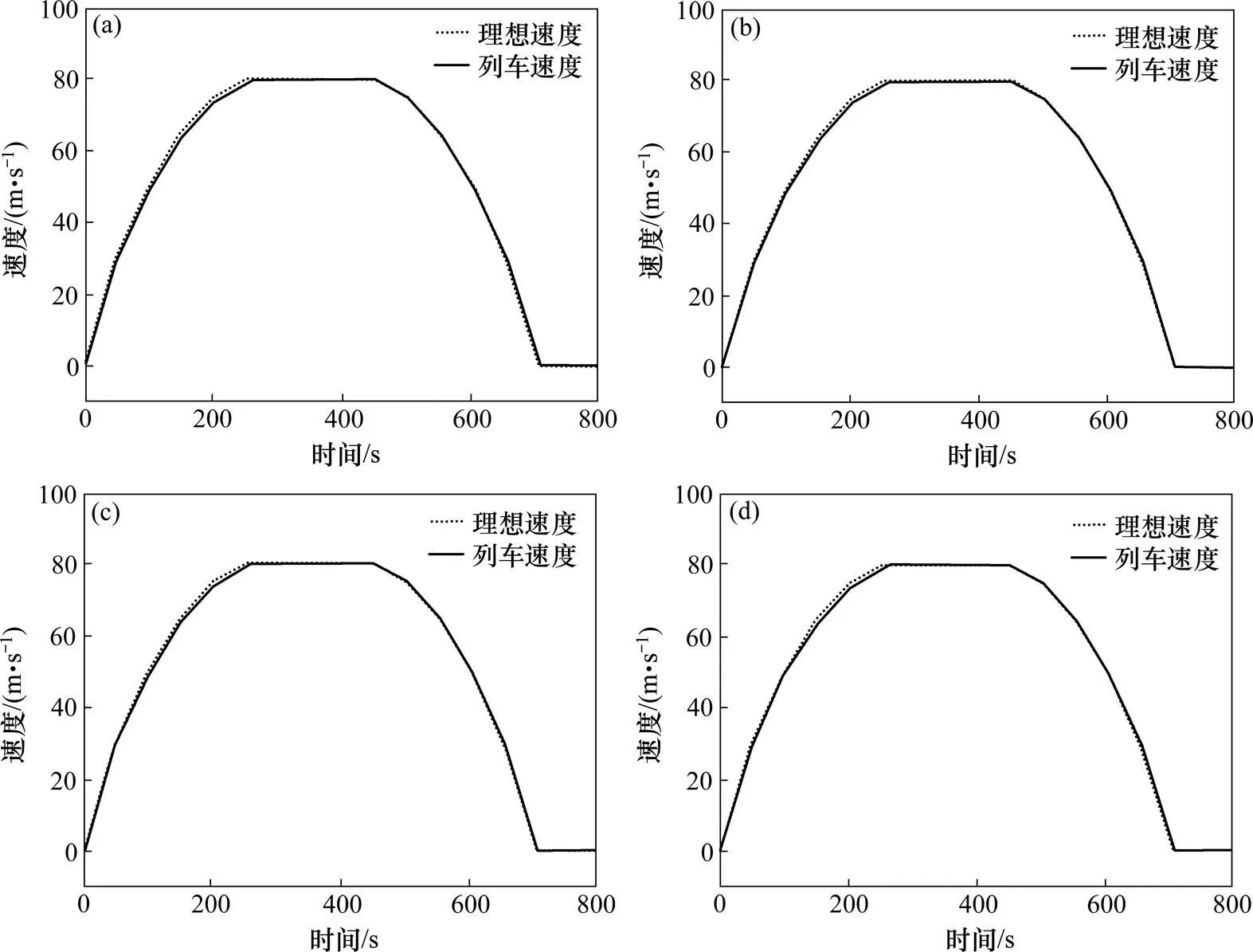
(a) 第1节车厢;(b) 第2节车厢;(c) 第3节车厢;(d) 第4节车厢
(a) 第1节车厢;(b) 第2节车厢;(c) 第3节车厢;(d) 第4节车厢

(a) 第1节车厢;(b) 第2节车厢;(c) 第3节车厢;(d) 第4节车厢
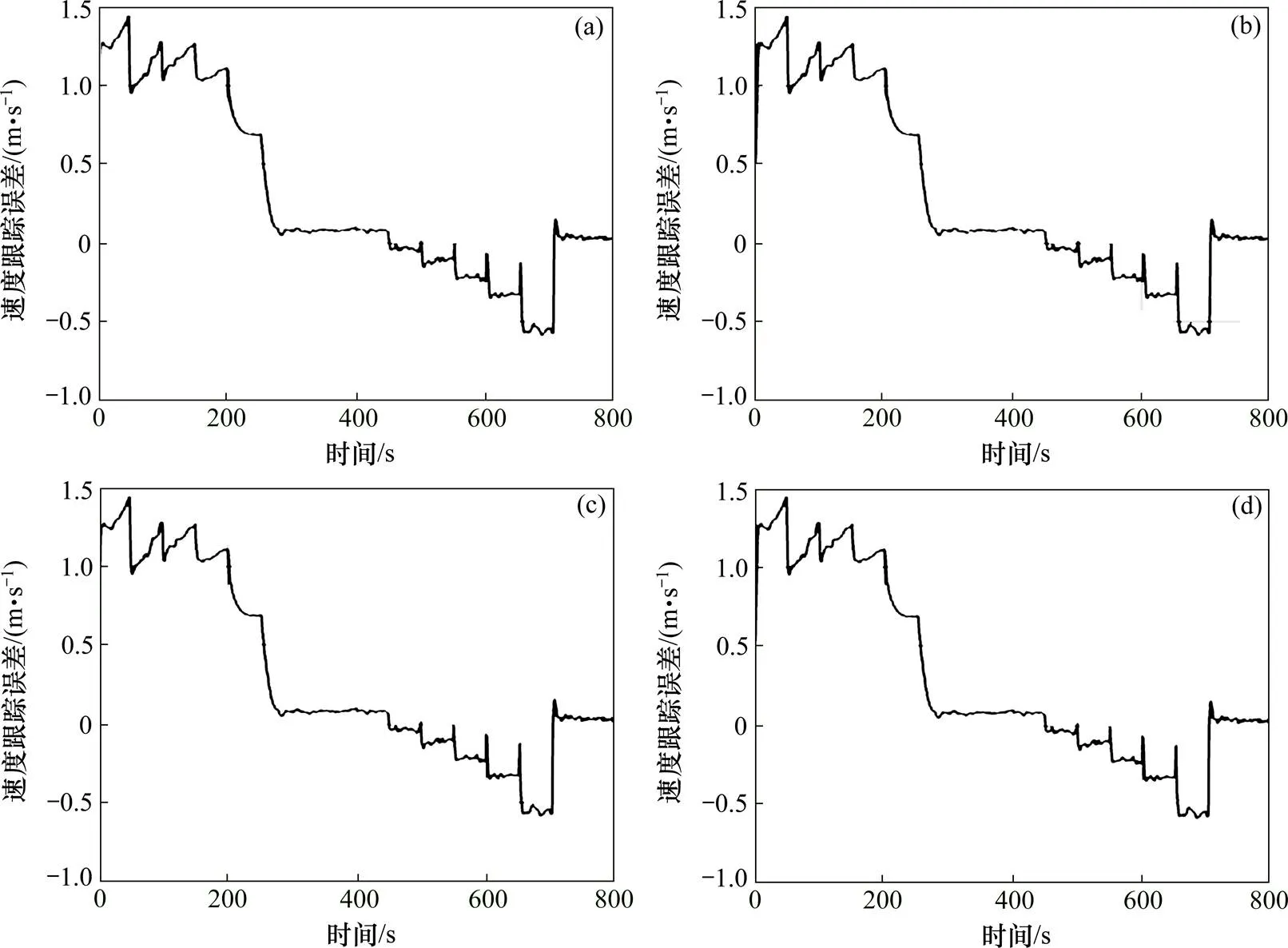
(a) 第1节车厢;(b) 第2节车厢;(c) 第3节车厢;(d) 第4节车厢
由以上结果可得,模糊控制的高速列车前4节车厢的最大速度跟踪误差分别为:1.446 0,1.446 1,1.446 0和1.446 2 m/s;平均速度跟踪误差分别为: 0.445 7,0.445 7,0.445 7和0.445 7 m/s;最大加速度分别为:0.529 5,0.529 4,0.529 4和0.529 3 m/s2;平均加速度分别为:0.173 3,0.173 2,0.173 1和0.173 1 m/s2。
为减小速度跟踪误差,对多质点模型高速列车用模糊预测控制器进行速度控制,以前4节车厢为例,得到的仿真结果如图10所示,速度跟踪误差如图11所示,加速度变化曲线如图12所示。

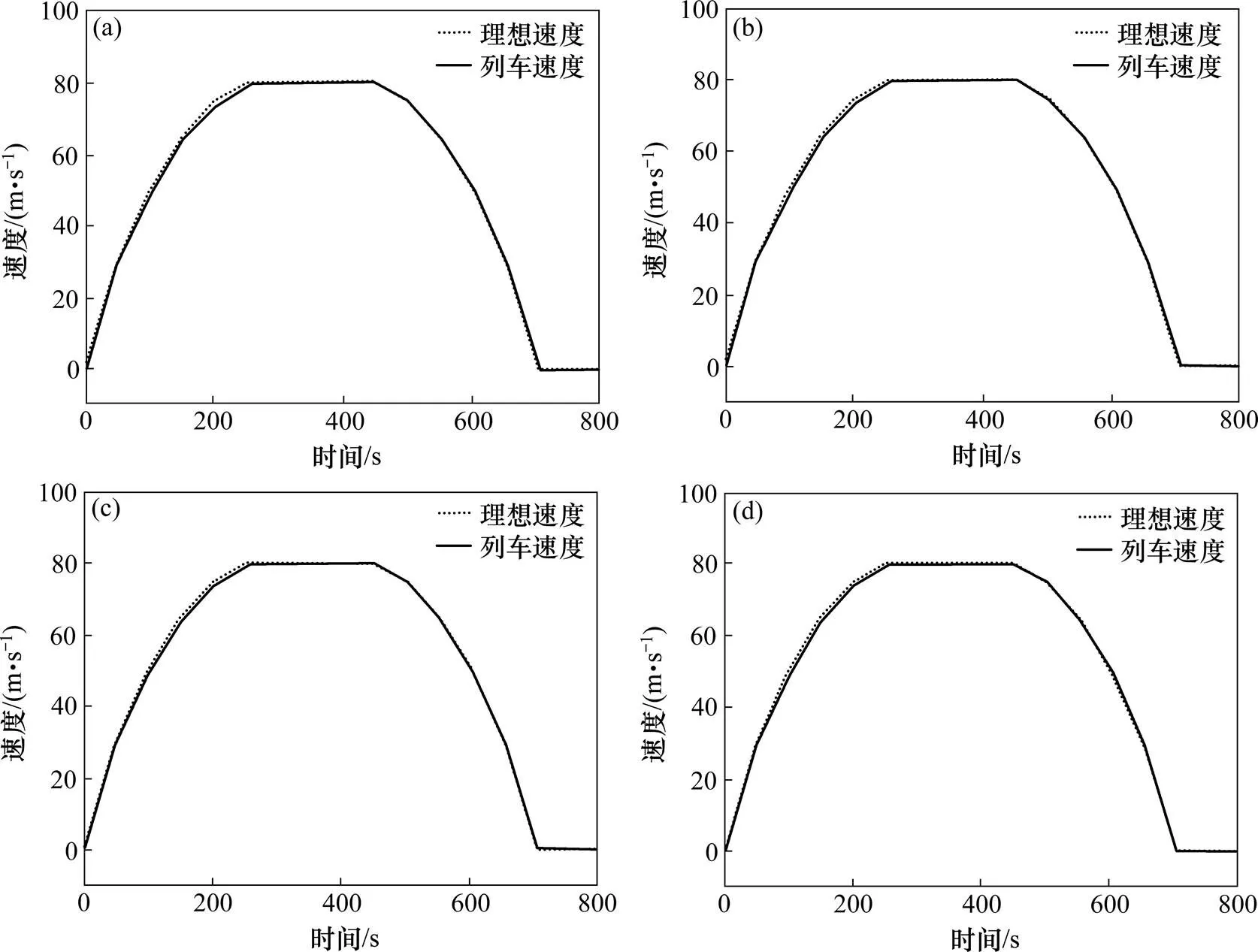
(a) 第1节车厢;(b) 第2节车厢;(c) 第3节车厢;(d) 第4节车厢
由以上结果可得,模糊预测控制的高速列车前4节车厢的最大速度跟踪误差分别为:0.998 3,0.998 6,0.998 5和0.998 8 m/s;平均速度跟踪误差分别为:0.339 9,0.339 9,0.339 9和0.339 9 m/s;最大加速度分别为:0.519 9,0.520 2,0.520 2和 0.520 4 m/s2;平均加速度分别为:0.160 1,0.160 1 ,0.160 1和0.160 1 m/s2。
以第1节车厢为例,多质点模型高速列车模糊预测控制与模糊控制相比,最大速度跟踪误差减小了31%,平均速度跟踪误差减小了24%,最大加速度减少了2%,平均加速度减少了8%。
假设列车行至16 000 m处时有个坡度为12, 长为2 000 m的坡。则当线路上无坡时单质点模型高速列车模糊预测控制的速度跟踪曲线如图13所示,速度跟踪误差如图14所示;当线路上有坡时单质点模型高速列车模糊预测控制的速度跟踪曲线如图15所示,速度跟踪误差如图16所示。
由以上结果可得,线路上无坡时,当高速列车运行到16 000 m处时,单质点模型高速列车模糊预测控制的速度跟踪误差为0.000 5 m/s,而线路上有坡时的速度跟踪误差为0.449 3 m/s。经计算得,线路上有坡时的跟踪速度变化量为0.448 8 m/s,相比较于线路上无坡时的列车速度变化了0.56%。

(a) 第1节车厢;(b) 第2节车厢;(c) 第3节车厢;(d) 第4节车厢

图13 无坡时单质点模型速度跟踪曲线
对多质点模型高速列车,以前4节车厢为例,线路上无坡时,高速列车模糊预测控制的速度跟踪曲线与速度跟踪误差如图10和图11所示;而线路上有坡时的速度跟踪曲线与速度跟踪误差如图17和图18所示。
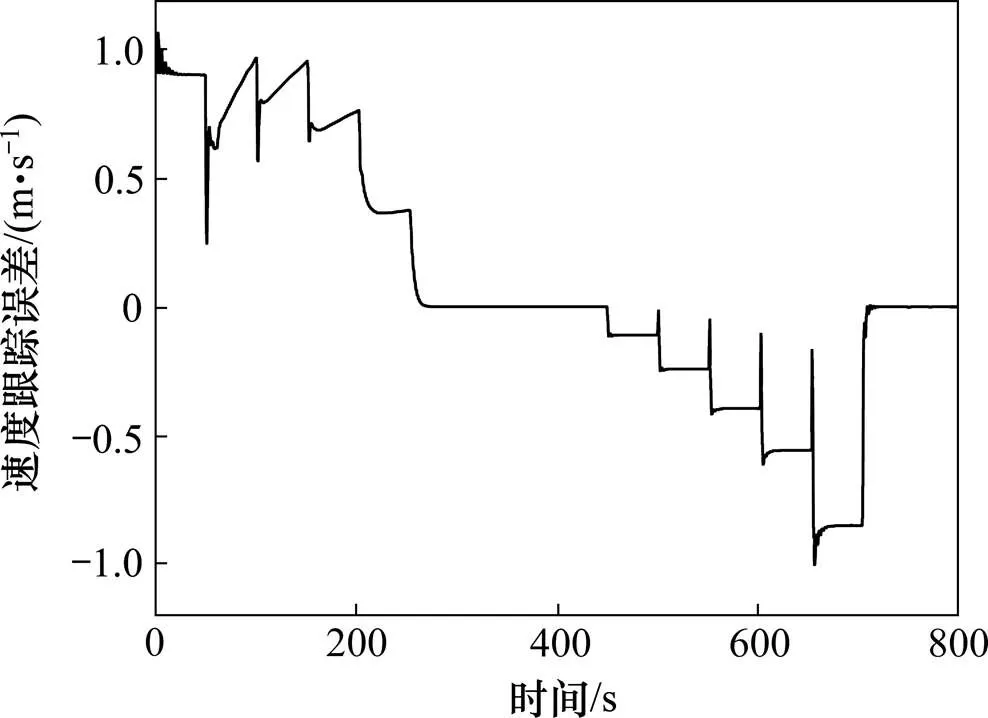
图14 无坡时单质点模型速度跟踪误差

图15 有坡时单质点模型速度跟踪曲线
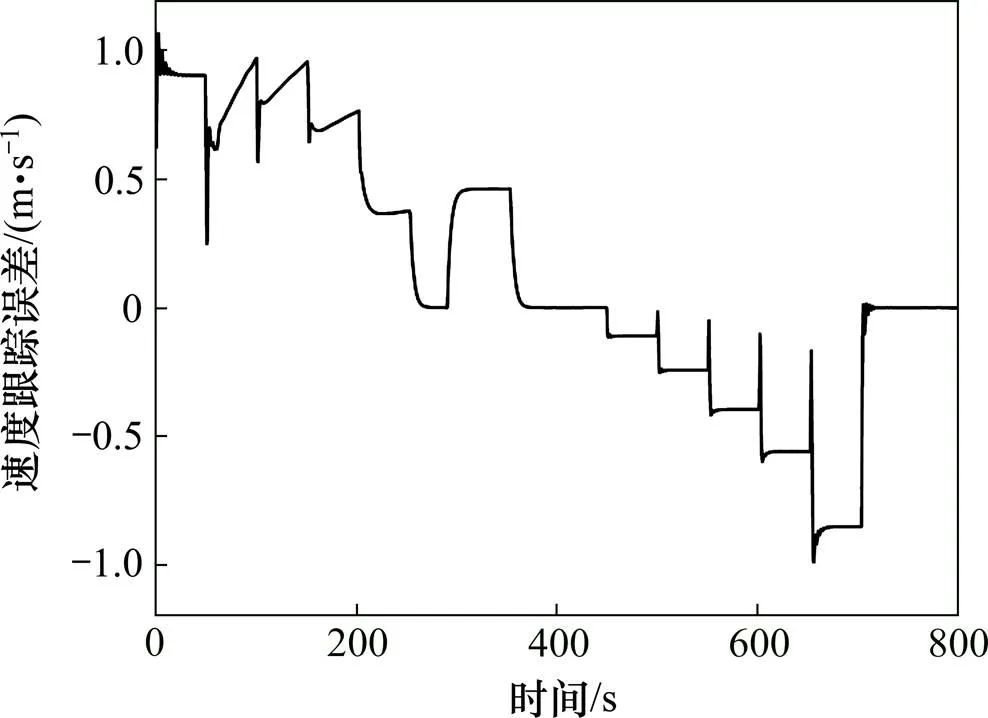
图16 有坡时单质点模型速度跟踪误差
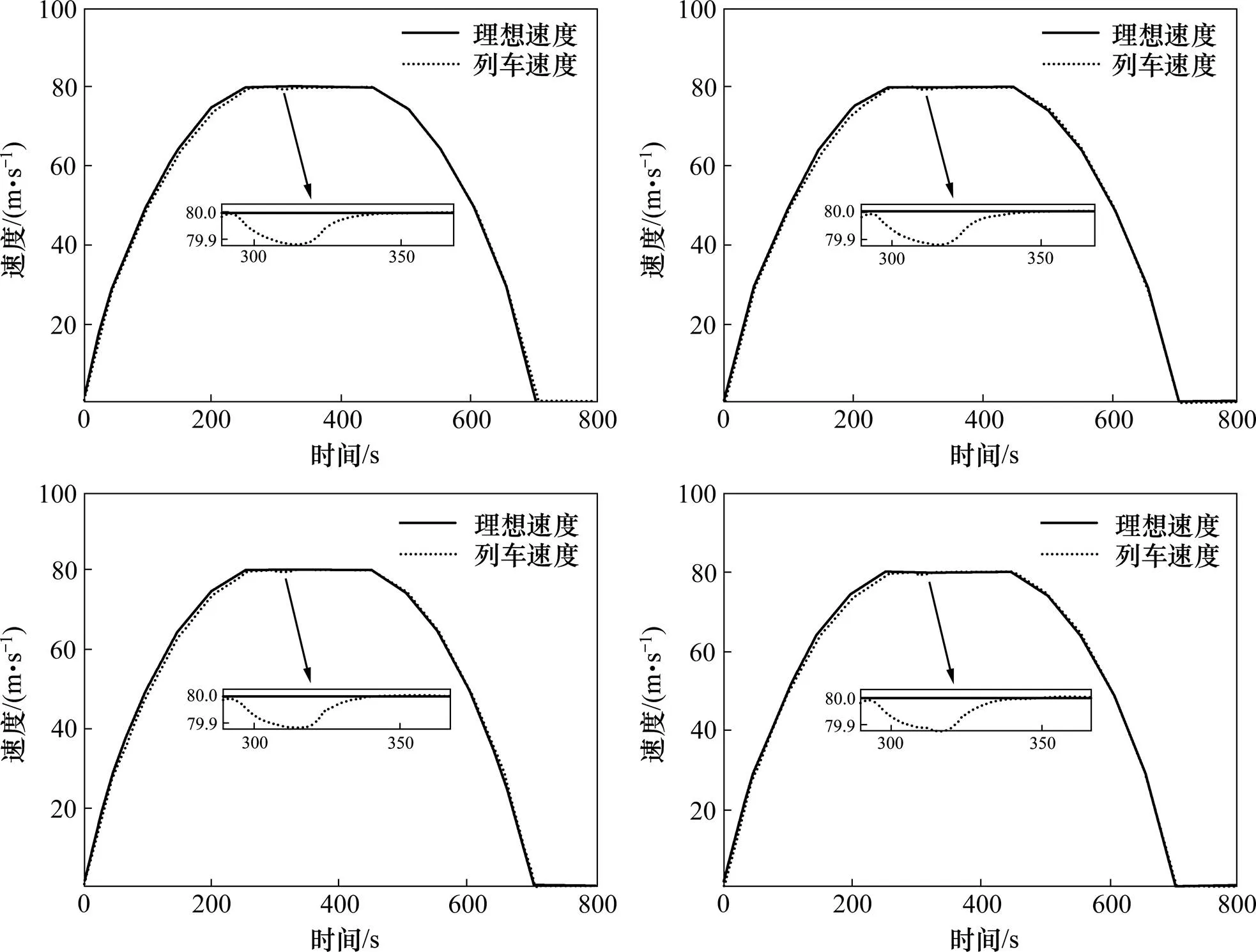
图17 有坡时多质点模型高速列车模糊预测控制速度跟踪曲线
由以上结果可得,以第1节车厢为例,当线路上无坡时,在高速列车运行到16 km处时,多质点模型的模糊预测控制速度跟踪误差为0.001 7 m/s,而线路上有坡时的速度跟踪误差为0.130 6 m/s。经计算得,线路上有坡时的跟踪速度变化量为0.128 9 m/s,相比较于线路上无坡时的跟踪速度变化了0.16%。
由上述结果分析可以看出,对高速列车进行多质点建模能够有效地解决列车在通过变坡处的速度跳变问题,列车在变曲率处的速度跳变问题与之相似。

(a) 第1节车厢;(b) 第2节车厢;(c) 第3节车厢;(d) 第4节车厢
4 结论
1) 对单质点模型的高速列车进行速度控制,当列车在通过变坡点或变曲率点时速度会发生跳变,产生较大的控制误差。
2) 高速列车运行时,在深入分析各节车厢的受力的基础上建立的多质点列车模型,能有效地解决列车在通过变坡点和变曲率点时的速度跳变问题。
3) 在控制算法方面,把预测控制的优点结合到模糊控制中,针对多质点模型的高速列车设计的模糊预测控制器,能有效地减小速度跟踪误差并且改善加速度的波动情况,提高了列车运行的速度控制精度和舒适度。
[1] YANG C D, SUN Yunping. Mixed H2/H cruise controller design for high speed train[J]. International Journal of Control, 2001, 74(9): 905−920.
[2] LIN C J, Tsai S H, Chen C L, et al. Extended sliding- mode controller for high speed train[C]// 2010 International Conference on System Science and Engineering, July 1-3, 2010. Taipei, Taiwan, China. New York, USA: IEEE, 2010.
[3] 何晓琼, 彭旭, 周瑛英, 等. 基于多质点动车组制动模型的动态牵引负荷[J]. 西南交通大学学报, 2013, 48(5): 878−884. HE Xiaoqiong, PENG Xu, ZHOU Yingying, et al. Dynamic traction load of a multi-mass EMU braking model[J]. Journal of Southwest Jiaotong University, 2013, 48(5): 878−884.
[4] SONG Qi, SONG Yongduan, TANG Tao, et al. Computationally inexpensive tracking control of high- speed trains with traction/braking saturation[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4): 1116−1125.
[5] SONG Qi, SONG Yongduan, TANG Tao, et al. Computationally inexpensive tracking control of high- speed trains with traction/braking saturation[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4): 1116−1125.
[6] [6] ZHANG Lijun, ZHUAN Xiangtao. Braking-penalized receding horizon control of heavy-haul trains[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(4): 1620−1628.
[7] ZHANG Lijun, ZHUAN Xiangtao. Optimal operation of heavy-haul trains equipped with electronically controlled pneumatic brake systems using model predictive control methodology[J]. IEEE Transactions on Control Systems Technology, 2014, 22(1): 13−22.
[8] ZHANG Lijun, ZHUAN Xiangtao. Development of an optimal operation approach in the MPC framework for heavy-haul trains[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(3): 1391−1400.
[9] 张驰, 谭南林, 周挺, 等. 基于分数阶PID控制器的地铁列车优化控制研究[J]. 铁道学报, 2018, 40(10): 8− 14. ZHANG Chi, TAN Nanlin, ZHOU Ting, et al. Research on optimal control of subway train based on fractional order PID controller[J]. Journal of the China Railway Society, 2018, 40(10): 8−14.
[10] 陈小强, 马泳娟, 侯涛, 等. 预测模糊PID在高速列车速度控制中的研究[J]. 系统仿真学报, 2014, 26(1): 191−196, 201. CHEN Xiaoqiang, MA Yongjuan, HOU Tao, et al. Study on speed control of high-speed train based on predictive fuzzy PID control[J]. Journal of System Simulation, 2014, 26(1): 191−196, 201.
[11] YANG Hui, FU Yating, ZHANG Kunpeng. Generalized predictive control based on neurofuzzy model for electric multiple unit[C]// 2012 Third International Conference on Digital Manufacturing & Automation, July 31-August 2, 2012. Guilin, China. New York, USA: IEEE, 2012.
[12] Aradi S, Becsi T, Gaspar P. Design of predictive optimization method for energy-efficient operation of trains[C]// 2014 European Control Conference (ECC), June 24-27, 2014. Strasbourg, France. New York, USA: IEEE, 2014.
[13] 李中奇, 杨振村, 杨辉, 等. 高速列车双自适应广义预测控制方法[J]. 中国铁道科学, 2015, 36(6): 120−127. LI Zhongqi, YANG Zhencun, YANG Hui, et al. Generalized predictive control with dual adaptation method of high speed train[J]. China Railway Science, 2015, 36(6): 120−127.
[14] 孟建军, 刘震. 城轨列车精确停车智能控制算法研究与仿真[J/OL].计算机工程与应用.http:// kns.cnki. net/kcms/detail/11.2127.TP.20190302.0843.002.html MENG Jianjun, LIU Zhen. Research on intelligent algorithm for precise parking of urban rail transit based on predictive fuzzy PID[J/OL]. Computer Engineering and Applications. http://kns.cnki.net/kcms/detail/11.2127. TP.20190302.0843.002.html
[15] 杨辉, 刘盼, 李中奇. 基于Elman模型的高速列车速度跟踪控制[J]. 控制理论与应用, 2017, 34(1): 125−130. YANG Hui, LIU Pan, LI Zhongqi. Speed tracking control for high-speed train with an Elman model[J]. Control Theory & Applications, 2017, 34(1): 125−130.
Study on speed control of high-speed train based on multi-point model
HOU Tao, GUO Yangyang, CHEN Yu, YANG Hongkuo
(School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)
In previous studies on speed control of high-speed trains, the traditional single-point train model ignores the length of the train and the mutual influence between the carriages, so the speed of the train jumps when passing through the special line, resulting in a large speed control error. In view of the above problems, based on the train length information and the analysis of the force of each carriage, the multi-point model of high-speed train was established, and the corresponding fuzzy predictive controller was designed to study the train speed tracking control. The simulation results show that the multi-point model of the train can effectively solve the problem of speed jump when the train passes through the variable slope and curvature points, and reduce the speed control error. The fuzzy predictive controller designed for the train model can control the train to track the ideal speed curve operation and improve the speed control accuracy and ride comfort.
high-speed train; multi-point model; fuzzy predictive control; speed control; dynamic matrix control
TP273
A
1672 − 7029(2020)02 − 0314 − 12
10.19713/j.cnki.43−1423/u.T20190542
2019−06−17
兰州交通大学“百名青年优秀人才培养计划”基金资助项目;甘肃省高等学校科研资助项目(2017A-026)
侯涛(1975−),男,四川中江人,教授,博士,从事智能信息处理与智能控制研究;E−mail:ht_houtao@163.com
(编辑 蒋学东)

