基于贝叶斯优化SEIR模型的新型冠状病毒预测与分析

王 庆,陈俊熹,熊东平,何啸峰

(1.南华大学 计算机学院，湖南 衡阳 421001;2.南华大学 附属南华医院，湖南 衡阳 421000)

新型冠状病毒肺炎(Corona Virus Disease 2019，COVID-19)，简称“新冠肺炎”，是指2019年新型冠状病毒感染导致的肺炎[1-2]。国内外均受到了新型冠状病毒带来的巨大干扰，而该病毒与SARS[3]、中东呼吸综合征(MERS)[4]、HIV[5]等传染性疾病有所不同。SARS这类病毒主要表现为发病2～3天之后出现明显发热，发热程度比较高，病人呼吸困难，病情相对比较重，致死率相对较高。而新型冠状病毒肺炎的潜伏期一般在14天之内,病毒传染能力很强，传播能力比SARS、埃博拉病毒、H7N9强,传染性较高导致防疫非常困难。通过国家卫生健康委员会[6]公布的数据，截至3月21日24时，全国现有确诊人数5 549人，现有疑似人数118人，累计治愈人数72 244人，尚在医学观察10 071人。由于国家采取了有效的管控策略，我国的疫情形势正在逐渐好转。目前国外疫情则令人关注，疫情形势相对较重，各个国家正在积极地应对，同时我国也派出了相关专家援助共同对抗疫情。

1 相关工作

从疫情开始至今，已有相关研究团队对新型冠状病毒展开建模并进行分析，范如国[7]等对新冠病毒展开建模，对中国全境、湖北省尤其武汉市数据进行研究，分析了不同潜伏期天数对感染人数以及疫情拐点到来的时间影响。耿辉[8]等研究了国家采取的防护措施对病毒传播带来的影响，对比了停工停学不限制出行和限制出行对易感者、潜伏者、感染者和移除者的变化趋势。吉兆华[9]等用室模型拟合了全国及广东、河南、江苏、湖北、浙江5个省份1月份报告发病情况，根据模型预测病例数对实际病例数的解释度和分析群体防控度。张琳[10]则采用一般增长模型分3个阶段拟合了确诊人数，发现确诊人数在经历了初期(1月15日～1月27日)的无障碍指数增长，中期(1月27日～2月6日)的次指数增长后，已在2月6日进入了次线性增长阶段。周涛[11]等在对武汉新型冠状病毒感染肺炎基本再生数进行了预测，估计COVID-19的基本再生数在2.8～3.3之间。随着COVID-19疫情的发展与防控策略的不断加强，新型冠状病毒肺炎传播机理还需进一步研究。因此，研究针对如何科学高效地管控疫情，分析了国内外早期的疫情数据，对已有的数据进行数学建模，进而预测未来疫情的发展趋势，力图为疫情防控提供理论支持和实践指导。

2 基于贝叶斯优化SEIR模型的新冠肺炎疫情分析

2.1 数据来源

研究所使用的疫情数据来自于国家卫生健康委员会、湖北省卫健委[12]、湖南省卫健委[13]、安徽省卫健委[14]、陕西省卫健委[15]、甘肃省卫健委[16]以及根据github上Blankerl提供的数据接口(https://github.com/BlankerL/DXY-COVID-19-Data)所获得的疫情数据。依据疫情发展情况的不同，国内分析1月20日～2月16日的疫情数据，而国外研究2月22日～3月22日的疫情数据。

2.2 模型参数分析

通过模型辨识和参数估计，对SEIR模型中关键参数进行了分析，参数k代表一个感染者平均接触人数，k值的变化能够体现国家采取的防护措施带给病毒传播的影响。比如延长春节假期、企业延迟复工、学校延期开学、限制出行、居家隔离等，这些措施最大化地扼制了病毒的传播。而影响我国疫情发展的重要影响因素就是春运，春运前后全国及各省感染者平均接触人数随时间的变化如图1所示。由图1可以看出，1月24日之前完成的春运接触效果开始在1月25日之后显现，多地确实出现了春运带来的影响，k值有所上升。总体来说，全国的k值相对比较平稳，k约为10.23人，可以作为平均接触人数的参考。但是在1月24日之后，随着疫情的发展，国家采取了“封城”举措，全国多地采取一级响应，数学建模的参数需要动态调整，采取分层抽样来计算出新的k值。根据病毒传染程度分成5个等级，一级为最严重，五级为轻微，然后进行加权平均，结果计算可得k_new约为8.70人。另外，还计算了国家采取的种种防控手段对平均接触人数带来的影响因子(k_changed_ratio)，利用公式k_changed-ratio=k/k_new，计算得出k_changed_ratio约为1.16。k_new的值相比春运之前的k值有所减小，说明国家采取的管控措施对病毒的抑制起到了一定的影响，并在之后效果会更加显著。疫情严重程度的关键是防控因子的研究，为疾病预防控制部门提供重要的决策依据。

2.3 贝叶斯优化方法

(1)贝叶斯优化过程分析。针对研究需要解决预测疫情感染人数以及拐点到来的问题，提出了贝叶斯优化的方法，该方法能够有效快速地寻找到所要解决问题的最优参数，省去了根据人工经验调参所花费的时间。贝叶斯优化主要面向的问题场景是：

X*=argmaxf(x)(x∈S),

(1)

式中,S是x变量的候选集，即参数x可能取值的集合。目标从集合S中选取一个x，使得f(x)的值最大或最小。这里f(x)具体公式形态可能无法得知，即黑盒函数。但是可以选择一个x，通过实验或者观察得出f(x)的值。贝叶斯优化的流程图如图2所示。

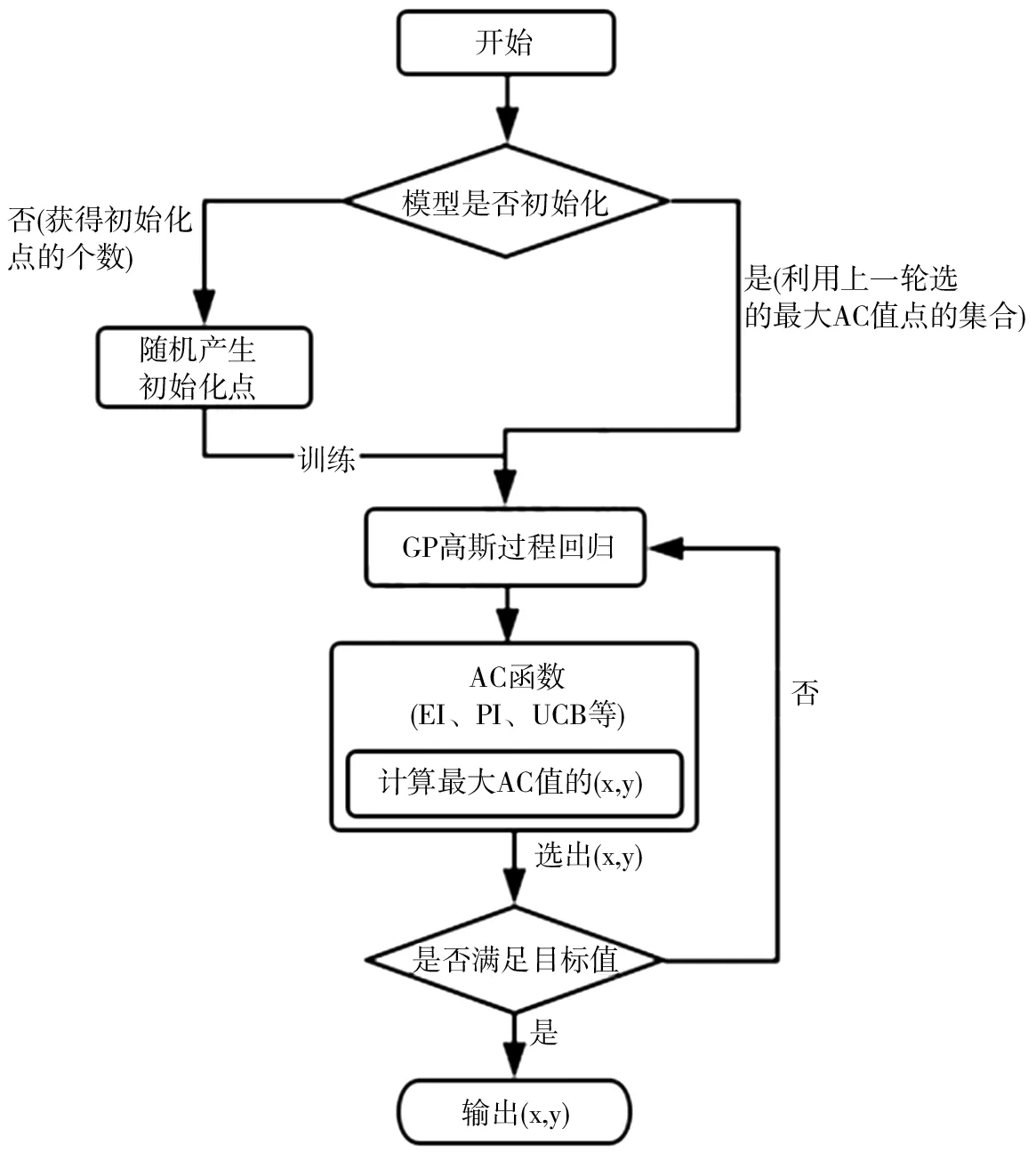
图2 贝叶斯优化流程图

贝叶斯优化[17-18]有两个核心过程，先验函数(Prior Function,PF)与采集函数(Acquisition Function,AC)，采集函数也叫效能函数(Utility Funtcion)。在贝叶斯决策理论的框架下，许多采集函数可以解释为在点x评估f相关的预期损失，然后通常选择具有最低预期损失的点。PF主要利用高斯过程回归，AC主要包括EI、PI、UCB这几种方法，接下来简要介绍一下AC的几种常用方法。

PI(Probability of Improvement):假设f′=minf这个f′表示目前已知的f的最小值。接着定义采集函数如下：

(2)

把u(x)理解成一个奖励函数，如果f(x)不大于f′就有奖励，反之没有。改进的采集函数作为变量x的期望函数如下：

(3)

最后aPI(x)的最大值即可求出基于高斯分布满足要求的变量x。

EI(Expected Improvement):上述的PI函数的缺点是有可能找到的是局部最优点，而不是全局最优点。而EI函数则可以找出全局最优点。f′的定义和上述一样，f′=minf。但是采集函数如下：

u(x)=max(0,f′-f(x)),

(4)

最终关于变量x的采集函数如式(5)所示：

(f′-u(x))Φ(f′;u(x),K(x,x))+K(x,x))N(f′;u(x),K(x,x)),

(5)

通过计算使得aEI值最大的点即为最优点。式(5)中有两个组成部分,要使得式(5)值最大则需要同时优化左右两个部分：左边需要尽可能地减少μ(x)；右边需要尽可能地增大方差(或协方差)K(x,x)。在探索(Exploration)和利用(Exploitation)此类问题上是一个典型理论。

UCB(Upper Confidence Bound):UCB可以简单地理解为上置信边界，UCB通常采用最大化f而不是最小化f来描述。但是在最小化的情况下，采集函数将采取以下形式：

aUCB(x)=u(x)-βσ(x),

(6)

(2)贝叶斯优化结果分析。为了提高SEIR模型计算效率和分析精确度，需要优化α和β这些主要参数。常用的调参方式有网格搜索(Grid Search)和随机搜索(Random Search)。Grid Search是全空间扫描，但较慢。而Random Search虽然快，但可能错失空间上的一些重要的点，精度不够。因此，研究选择贝叶斯优化方法来调整参数。该算法速度较快、效果较好。贝叶斯优化利用平滑性而无需计算梯度，可处理大量变量并行优化。研究分别分析我国和意大利的优化参数α和β，将二者迭代优化次数均设置为1 000次，经过1 000次的迭代优化之后可以得出我国和意大利α和β的参数结果随着时间步的变化分别如图3和图4所示。由图3可以看出，我国疫情随着参数α和β的迭代次数不断增加，α在0.26～0.30越来越密集，β在0.050～0.100越来越密集，等到1 000次迭代优化之后，可以得出α和β的最优解分别为0.28和0.08。由图4可以看出，意大利疫情随着参数α和β的迭代次数不断增加，α在0.16～0.20越来越密集，而β在0.050～0.075越来越密集，等到1 000次迭代优化之后，可以得出α和β的最优解分别为0.18和0.06。

图3 中国α、β随着时间步t的变化图

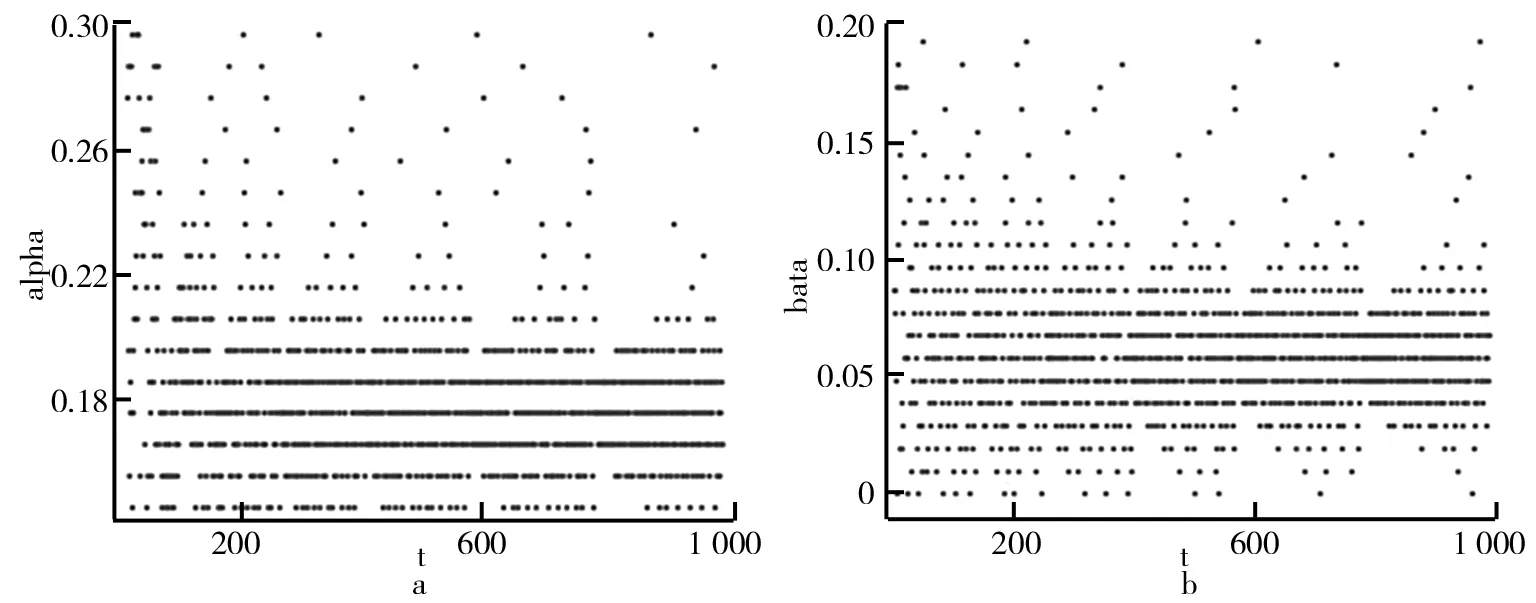
图4 意大利α、β随着时间步t的变化图

2.4 基于贝叶斯优化的SEIR模型

在传染病SEIR模型中，种群(Population)内的N个个体的状态可分为如下几类：(1)易染状态S(Susceptible)，即健康状态，可被感染的个体；(2)潜伏状态E(Exposed)，处于传染病潜伏期的个体；(3)感染状态I(Infected)，处于感染状态的个体还能够感染健康状态的个体；(4)移除状态R(Removed,Refractory or Recovered)，为被隔离或因病愈而具有免疫力的人。传统的SEIR模型只是考虑了有潜伏者(Exposed)这种人群，但是并没有考虑到潜伏者也具有传染性。为了适应COVID-19疫情发展与不断加强的防控策略，研究中的SEIR模型考虑潜伏者的传染性，根据春运防护前后病毒传播机制不同的实际问题，模型分为春运前后两个阶段，利用贝叶斯优化方法更新参数，改进的SEIR模型如图5所示，模型的微分方程如式(7)所示。

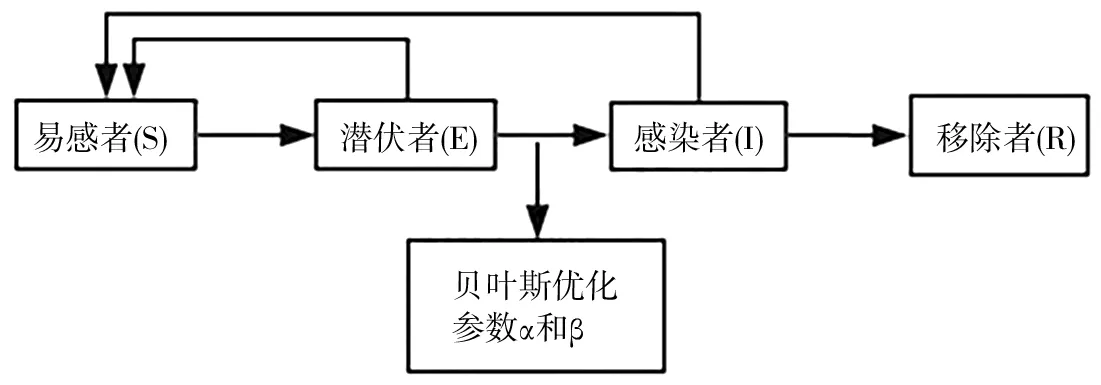
图5 改进的SEIR模型示意图

(7)

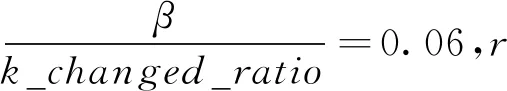
3 结果与分析

新冠病毒治愈率、死亡率、重症率变化如图6所示。由图6可知，我国新冠肺炎的整体趋势随着时间的推移、治疗经验和手段的不断丰富、全国医院紧急驰援武汉，治愈人数比例有了明显的上升，重症和死亡人数比例在不断下降，感染人数不再上升，综合表明病毒疫情正在被逐渐控制。将所有省份按确诊人数进行新型冠状病毒感染情况等级的划分，一级为最严重，五级为最轻微，采用分层抽样的方法抽取了湖北、湖南、安徽、陕西和甘肃5个省份来进行分析。研究将针对各个省份的确诊人数、治愈率、确诊人数增长率等方面进行分析。4个省在1月20日～2月16日确诊人数变化图如图7所示。由图7可知，湖南和安徽的确诊人数相较其他两省增长比较明显，原因和每个省份的地理位置密切相关，前面两省与湖北省接壤，地理位置比较靠近，所以病毒传播的比较快速，而后两省离得相对较远，所以传播速度慢，同时各个省份积极应对此次疫情，从图7中还可以看出，确诊人数慢慢变得平稳起来。

图6 我国新冠病毒治愈率、死亡率、重症率变化图图7 4个省在1月20日～2月16日期间确诊人数变化图

截至目前，中国疫情形势正在逐渐好转，作为中国疫情发源地的武汉也已经连续多天新增人数为0，但相同时间的国外疫情变得非常严重，意大利、美国、法国、德国、伊朗等国家确诊人数在不断地攀升。研究选取了疫情发展相对比较严重的5个国家进行分析，即意大利、美国、法国、德国和伊朗。通过分析新增人数这个指标来反映疫情的严重程度。国外新冠病毒从2月22日～3月22日的新增人数趋势变化图如图8所示，从图8中可以清晰地看出，在第5天(2月27日)的时候，5个国家新增人数几乎为0，但是从第20天(3月13日)开始，新增人数趋势愈加明显，5个国家中除了伊朗比较稳定之外，其他的国家都以不同程度在增长，而新增人数最明显的就是美国，单日新增人数能够高达上万人，从而可以推测出美国未来一段时间内疫情会继续呈爆发式增长。因此，各国政府必须采取强有力的措施来更好地应对和管控疫情。

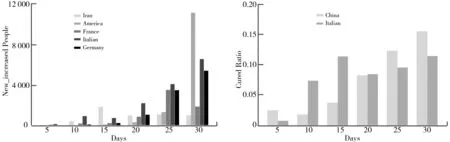
图8 国外新冠病毒2月22日～3月22日新增人数变化图 图9 中国和意大利治愈率对比图

据目前全球疫情数据可知，意大利现在是国外疫情非常严重的国家之一。中国和意大利治愈率对比图如图9所示。由图9可以看出，中国和意大利的治愈率都在逐步地提高，但是在疫情开始的20天之内，意大利的治愈率相比我国来说高一点。但是在第20天之后，我国的治愈率远超意大利，说明我国投入大量的医疗设备以及全国医院驰援武汉等强有力的防控措施使疫情得到大大减缓。意大利可以借鉴我国的做法，尽早尽快控制疫情。

研究基于贝叶斯优化SEIR模型拟合了国内自1月20日～2月16日的数据，结果如图10所示。通过图10a可以看出，该模型能够较好地拟合真实数据，预测峰值在79 107人，预测拐点在2月27日，可以较好地用来作为第二阶段模型预测的依据。由图10b可以看出，曲线拟合贴近真实数据，预测数据显示峰值是在81 314人，疫情拐点在2月25日。春运前与春运后的与第一阶段相比预测拐点稍有变化，这与治愈率γ的变化有关。随着γ的提高，疫情的拐点提前出现并且峰值也将稳定或者下降。但是总体来说，峰值稳定在2月25日至3月上旬之间。意大利确诊人数及拐点预测结果如图11所示。由图11可见，改进的SEIR模型对意大利确诊人数的拟合结果，显示峰值约在14万人左右，而疫情拐点也将在4月21日左右显现，这说明目前意大利的疫情形式还是比较严峻，需要加大防控力度，认真对待此次疫情，才能尽早地控制住疫情。

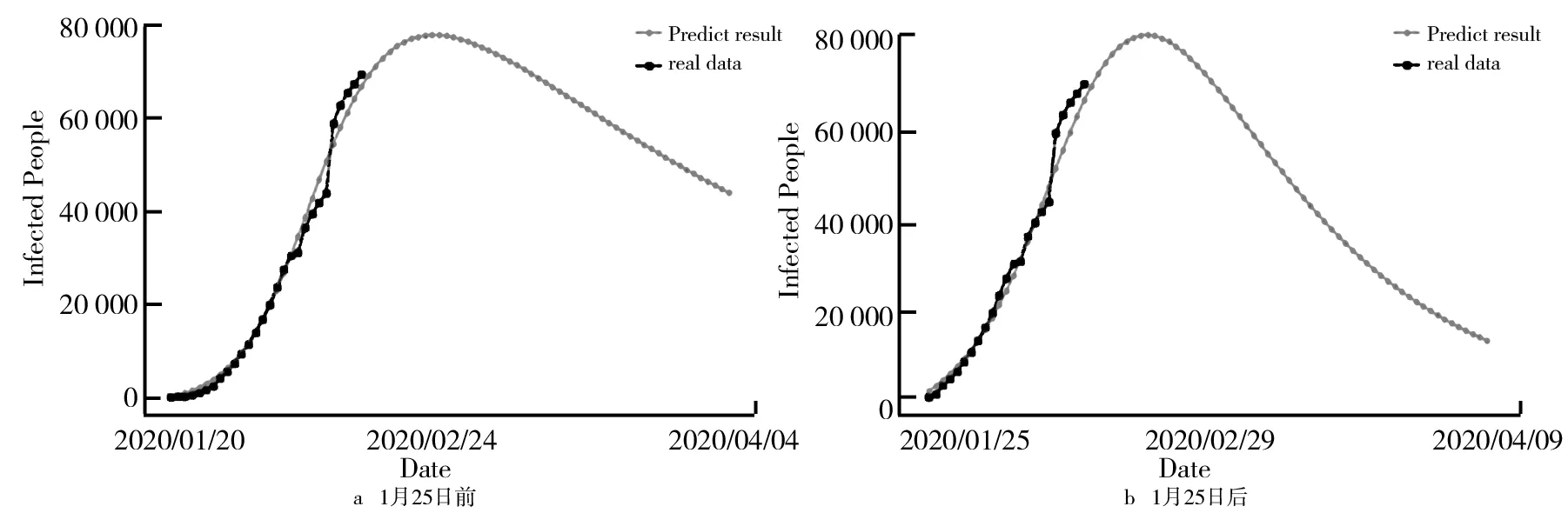
图10 中国1月25日前、后确诊人数及拐点拟合结果

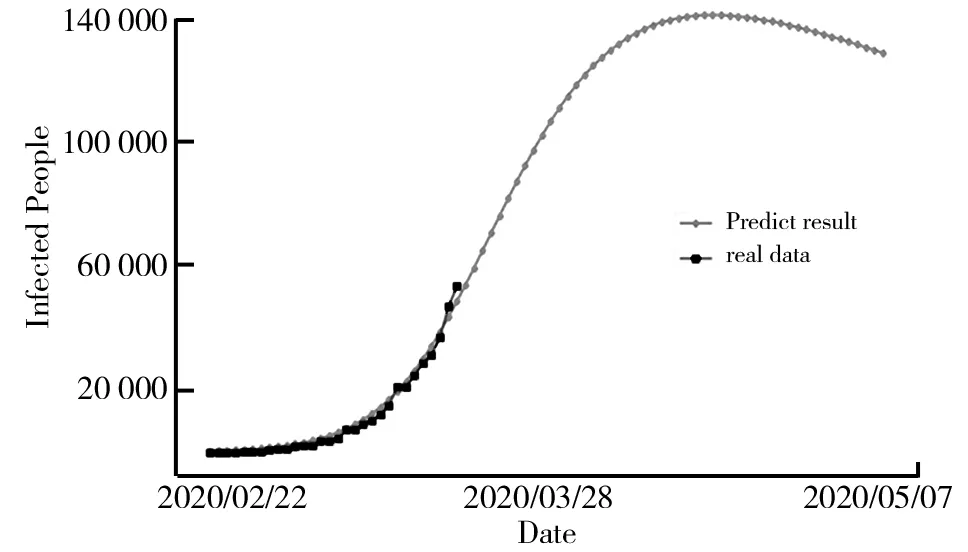
图11 意大利确诊人数及拐点预测结果

4 总结

研究基于SEIR模型来对新型冠状病毒预测与分析，同时运用了贝叶斯优化方法来搜索模型的最优超参数，提高了模型预测的效果。分析了国内外疫情的发展变化情况，分别对中国和意大利的疫情进行仿真和拐点预测，国内的预测图反应了管控措施给疫情带来的影响，使拐点提前并且在其之后感染人数下降速率加快。结果表明，模型适用性较优，能够较好地拟合曲线并对短期内疫情进行预测，能够提供一定的理论依据和指导意义。但是由于目前疫情还有很多未知因素，模型不可避免地会与现实存在一定差异，导致结果可能会存在一些误差。国外形势依旧严峻，应该加大防控力度，防护措施应做到快速并且到位，可以借鉴中国的做法，才能更好地应对此次疫情。