一种新的多涡卷混沌模型在图像加密中的应用

刘 嵩， 韦亚萍， 刘静漪， 张国平

(1.华中师范大学物理科学与技术学院， 武汉 430070；2.湖北民族大学新材料与机电工程学院， 湖北 恩施 445000)

混沌是非线性动力系统的一种运动形式，描述了确定性非线性系统中的复杂现象.自Lorenz于1963年首次在确定性方程中发现混沌现象以来，学者们对混沌系统展开了广泛深入的研究，其理论已广泛的应用于生物医学、信息科学、气象学、图像处理、天文学、经济学等领域[1-3]．

混沌系统具有遍历性、有界性、对初始条件敏感等特征，非常符合数字图像加密的需求，引起了图像加密领域研究者的密切关注[4-5].文献[6]改进了Logistic混沌，采用扩散-置乱-扩散的方法对图像进行加密，降低了有限精度效应，提高了密钥空间.文献[7]生成了四维多翼超混沌吸引子，采用混合加密方法，消除了确定的明文密文映射关系.文献[8]分析了AES算法在处理大尺寸图像时效率不高，需要增加额外的计算时间.文献[9]设计了一种基于块加密认证的图像加密算法.文献[10]首先置乱明文图像的像素，然后通过混沌映射得到伪随机序列，再利用得到的伪随机序列与置乱图像进行异或操作实现像素扩散，最后通过S-Box进行像素灰度值替换得到密文图像，取得了较好的加密效果.文献[11]提出一种彩色图像加密方案，首先将彩色图像的3个分量合成为一个灰度图像，然后对图像像素分别进行行置乱和列置乱，实现图像加密．

采用轨迹简单的混沌系统组成的密码直接加密明文，能够相对较容易的被破解.与单涡卷混沌系统或者双涡卷混沌系统相比，多涡卷混沌系统控制参数更多，相应的密钥参数也就更多，而且在相空间中能呈现出复杂的多方向分布的网格状涡卷，涡卷的数量和形状等性能也可以由系统的参数来控制调整，因此具有更加复杂的动力学行为[12-15]，更有利于图像加密.鉴于此，本文从研究5阶线性系统出发，通过引入分段线性函数构造一个多涡卷混沌系统，将该混沌系统应用于一种新的“置乱+扩散”加密算法，获得了较为优越的加密效果．

1 一种新的多涡卷混沌系统的构建

首先构建一个新的5阶线性系统，该系统的雅克比矩阵为满秩，保证系统唯一的平衡点属于指标2的鞍焦平衡点[16].新的五阶线性系统描述为：

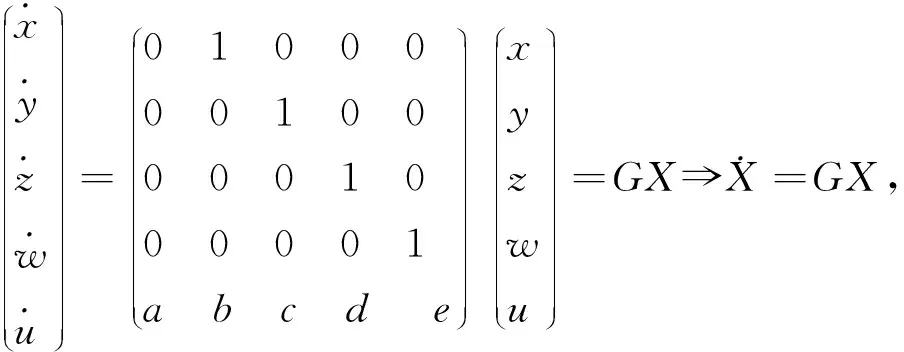
(1)

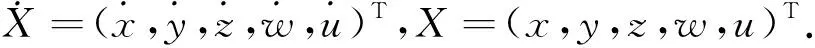
基于线性系统(1)，引入分段线性函数构建多涡卷混沌系统:

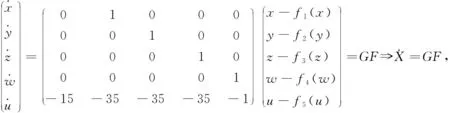
(2)

其中，fi(xi)是分段线性函数，为简便起见，选择阶跃函数构建分段线性函数，其表达式如式(3)和(4)，其中式(3)可以扩展的涡卷数目为 2Ni+2，式(4)可以拓展的涡卷数目为2Mi+1．

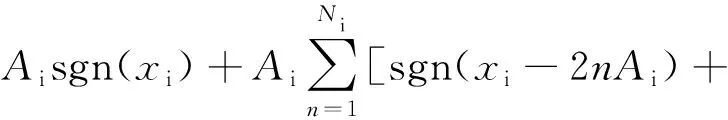
sgn(xi+2nAi)]，

(3)

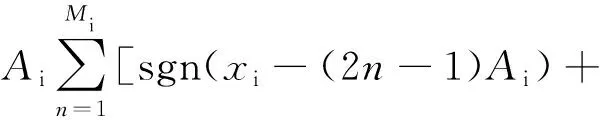
sgn(xi+(2n-1)Ai)].

(4)

如选择Ai=1，Mi=1，即

fi(xi)=sgn(xi-1)+sgn(xi+1).

(5)

系统可以在每一维空间方向上扩展3个涡卷，在MATLAB上的数值仿真如图1所示．

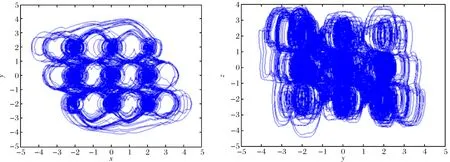
图1 五阶系统的相图Fig.1 Phase diagram of five-dimensional chaotic system

2 系统的基本动力学分析

2.1 系统的对称性与耗散性

从系统(2)可以看出，系统满足(x，y，z，w，u)→(-x，-y，-z，-w，-u)，因此该系统是关于坐标原点对称，从而为扩展多涡卷吸引子提供了可能.由于

(6)

所以系统(2)是耗散的，且以指数形式收敛，其运动轨迹被固定在一个吸引子上， 也说明混沌吸引子是存在的[17-18]．

2.2 平衡点

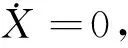
(7)

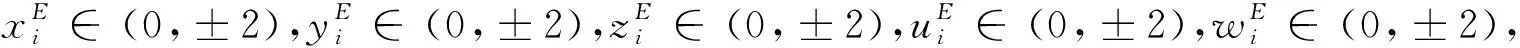
2.3 Lyapunov指数和维数

选择适当的初值，利用Wolf算法可以计算系统(2)的5个Lyapunov指数如下：

L1=0.1815，L2=0.1671，L3=-0.2208，

L4=-0.2212，L5=-0.5622，

系统有2个Lyapunov指数大于0，由此说明系统(2)是一个超混沌系统[19]．

系统(2)的维数计算如下.

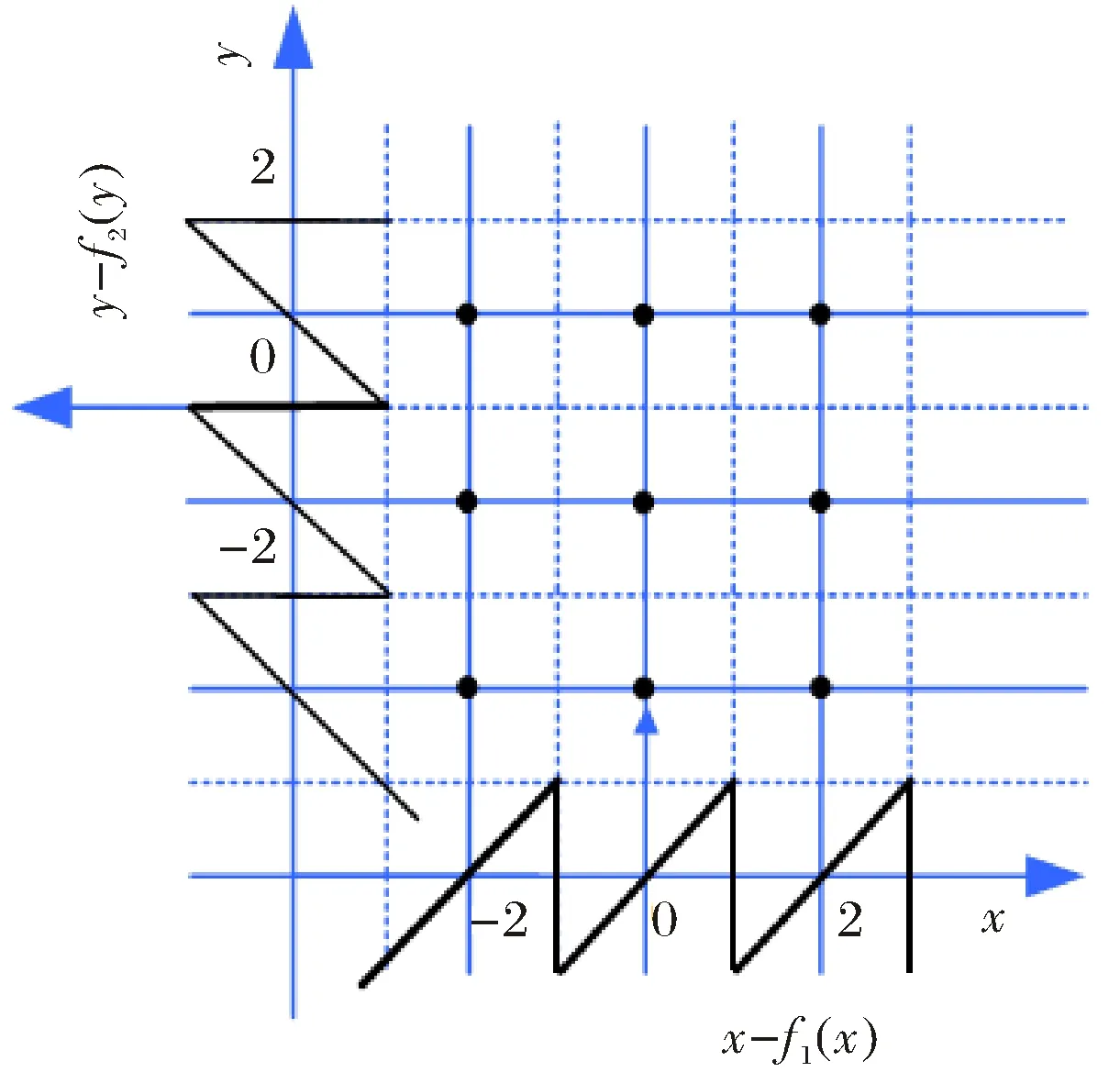
图2 指标2的鞍焦平衡点分布Fig.2 The saddle-focus equilibrium distribution of index 2

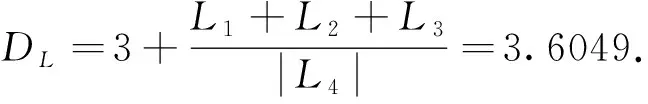
(8)

因此，系统(2) 的Lyapunov维数为分数维数，也验证了系统(2)为混沌[20]．

3 多涡卷混沌系统在图像加密中的应用

3.1 图像加密原理

混沌系统具有初值敏感性和不可预测性，是其能够应用于图像加密的根本原因.采用系统(2)构造的多涡卷混沌系统，用于图像加密的方案原理如图3所示．

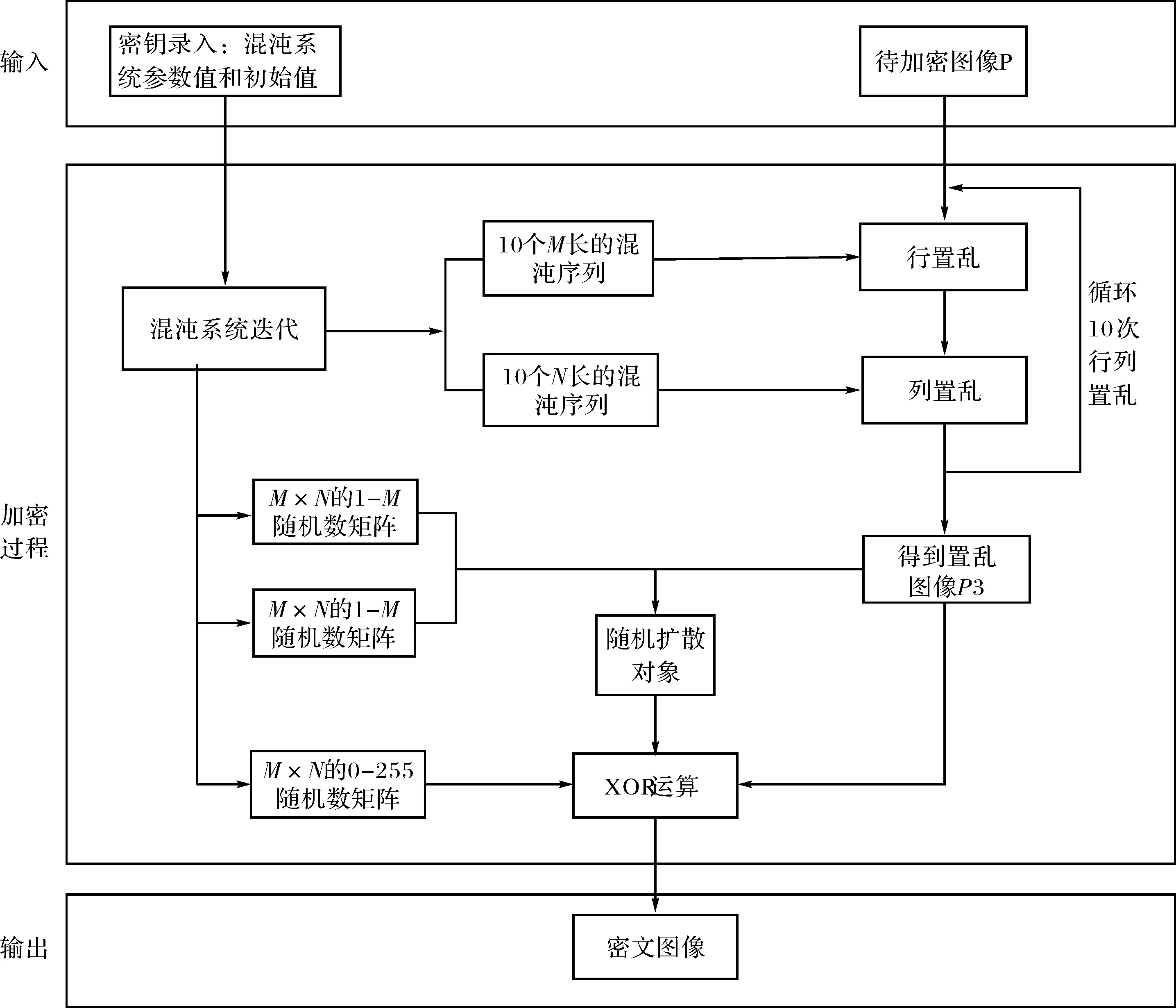
图3 图像加密的方案原理图Fig.3 Schematic diagram of image encryption scheme

本加密算法采用的密钥为key={x0y0z0w0u0}，主要步骤如下：

Step1: 读入待加密图像P，设图像大小为：M×N；

Step2: 录入混沌系统参数值和初值，通过迭代生成5个混沌序列x，y，z，w，u；

Step3: 利用公式(9)从x序列中截取10个M长的混沌序列row[10，M]，用于图像行置乱.利用公式(10)从y序列中截取10个N长的混沌序列column[10，N]，用于图像列置乱.舍去前10 000个元素以消除混沌序列的暂态效应；

row(i，∶)=x(i*1000+

10001∶i*1000+10000+M)，

(9)

column(i，∶)=y(i*1000+

10001∶i*1000+10000+N).

(10)

Step4: 按照式(11)将矩阵row(i，∶)按从小到大的顺序进行排序，得到一个位置序列L1，通过式(12)对图像P进行行置乱，得到图像P1；

[y1，L1]=sort(row(i，∶))，

(11)

P1(j，∶)=P(L1(j)，∶).

(12)

Step5: 同理，将矩阵column(i，∶)按从小到大的顺序进行排序，得到一个位置序列L2，通过式L2对图像P1进行列置乱，得到图像P2；

Step6: 重复Step4和Step5，依次对图像进行行置乱和列置乱，经过10轮得到置乱图像P3；

Step7: 通过式(13)、(14)首先提取z(10000+1，10000+M×N)、w(10000+1，10000+M×N)两个伪随机序列元素中小数点后第9～12位的二进制数字，再将提取的两个二进制数求模后加1，得到两个随机整数序列，最后将两个随机整数序列转换成M×N的矩阵

K1={k1(i，j)}，K2={k2(i，j)}；

K1=reshape(mod(mod(floor(z(10000+1∶10000+M×N)*1012)，1000)，M)+1，M，N)，

(13)

K2=reshape(mod(mod(floor(w(10000+1∶10000+M×N)*1012)，1000)，M)+1，M，N)，

(14)

Step8: 通过式(15)取u(10000+1，10000+M×N)元素中小数点后9～12位数字，对256求模，得到一个0～255的随机整数序列，将其转换成M×N的矩阵K3；

K3=reshape(mod(mod(floor(u(10000+1:10000+M×N)*1012)，1000)，M)+1，M，N).

(15)

Step9: 通过式(16)对图像P3进行像素值扩散，得到加密图像．

P3(i，j)=bitxor(bitxor(P3(i，j)，K3(i，j))，

P3(k1(i，j)，k2(i，j))).

(16)

当k1(i，j)=i且k2(i，j)=j时，式(16)修正为式(17)：

P3(i，j)=bitxor(P3(i，j)，K3(i，j)).

(17)

3.2 算法仿真结果

分别选取256×256的Lena、pepper和bridge灰度图作为初始实验图像，实验结果如图4所示，说明本算法可以完成图像的加密和解密操作．

图4 图像的加密结果仿真Fig.4 Image encryption simulation results

3.3 密匙空间分析

该算法密匙由5个状态变量的初值组成，假设计算机存储精度为10-15，则该算法的密匙空间为1015×1015×1015×1015×1015=1075.如果增加系统参数密匙，算法密匙空间将变得更大，也就具有更强的抵抗穷举暴力攻击的能力．

3.4 灰度直方图分析

直方图反映了数字图像像素的各个灰度级与其出现概率的关系，直方图分布越均匀，图像数据越随机，加密效果越好[21].图5给出了明文图像和密文图像的灰度直方图，从图5可以看出，经过加密运算，图像的灰度均匀性明显优于原始明文图像，且密文的像素值在整个像素取值范围内出现的概率趋于均等，有效地掩盖了明文图像像素值的分布情况，给攻击者利用统计分析方法破解密文图像增加了难度．

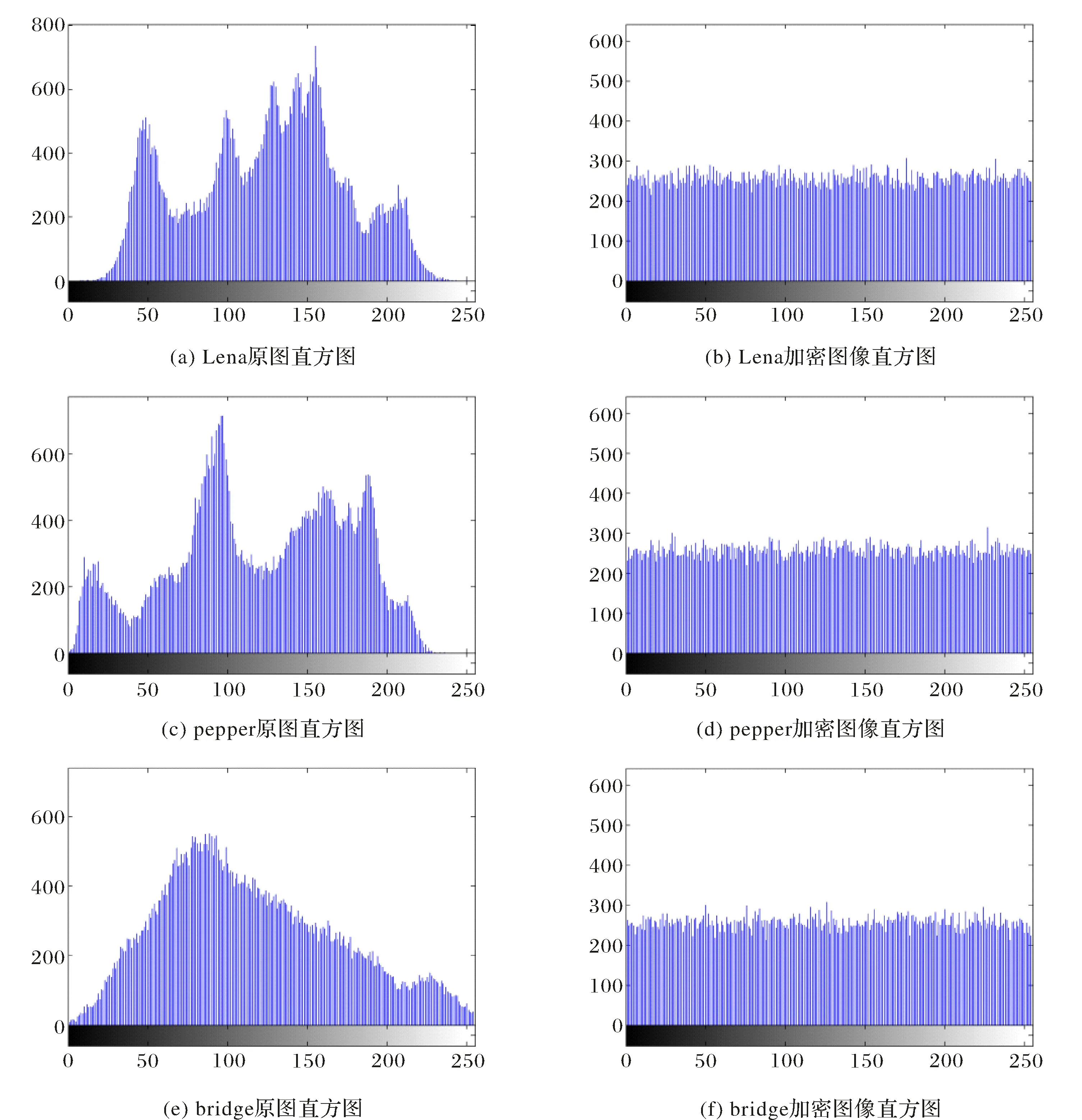
图5 原始图像和加密图像灰度值直方图Fig.5 Histogram of gray value of original image and encrypted image

3.5 相邻像素的相关系数

图像加密的目标之一就是减少图像相邻像素的相关性，使相关系数趋于 0.为了评估加密图像相邻像素的相关性，在3幅实验图像的明文图像和密文图像上分别随机选取1 000个像素，计算相关系数

(18)

其中，cov(x，y)、D(x)、E(x)分别为协方差、方差和均值：

(19)

图6是Lena原图和加密图像在水平、垂直和对角线三个方向的相关性.表1给出明文图像和密文图像在水平方向、垂直方向和对角线方向的相关系数.从图6可以看出明文图像相邻像素在水平方向、垂直方向和对角线方向上的相关性极强，而密文图像相邻像素在3个方向上相关性已经非常小，对应的相关系数非常接近0，说明明文图像的统计特性已很好地扩散到密文图像中．

表1 原始图像与密文图像相关系数的比较

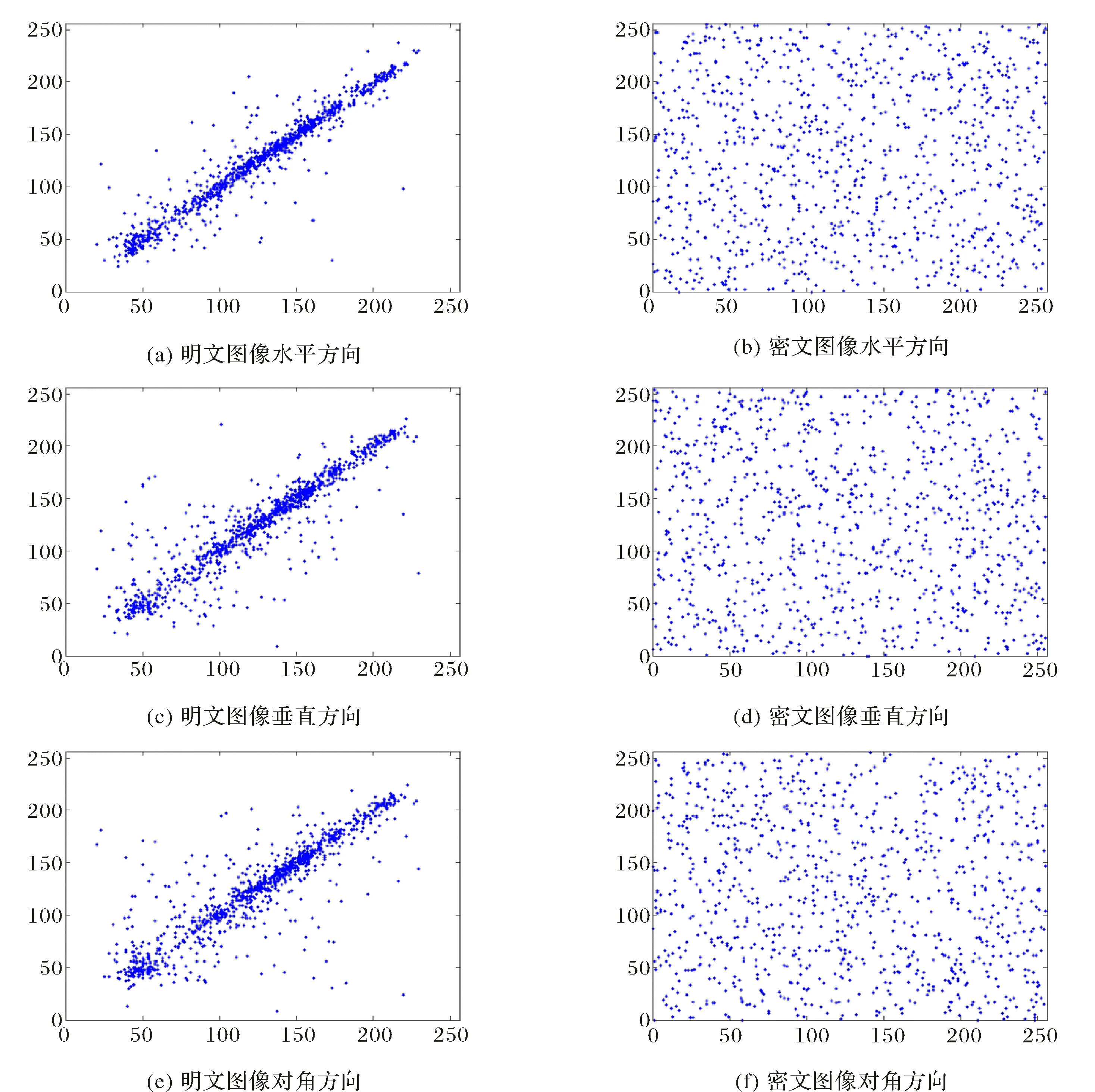
图6 Lena图像相邻像素相关性对比Fig.6 Correlation comparison of adjacent Lena pixels

3.6 密匙敏感性

密匙敏感性包括加密敏感性和解密敏感性，加密敏感性是用来表征在加密解密过程中，如果将加密密匙的某个参数值引入微弱的扰动，得到的密文图像与原密文图像的差异程度，解密敏感性是用来表征在解密同一密文图像时，对密匙引入微弱扰动，得到的解密图像与原明文图像的差异程度.如果差异显著，说明该算法具有较好的敏感性.像素变化比率(NPCR)和归一化平均变化程度(UACI)可以用来评价算法的加密敏感性[22-23]，其计算方法如下:

(20)

其中，M，N为图像大小，C1(i，j)，C2(i，j)为两个密文图像，NPCR和UACI的理想值为99.6094%和33.4635%.为评估该算法的加密敏感性，在图像加密过程中，分别对五个初值加以微弱扰动，相应的测试结果如表2所示.从表2可以看出在加密过程中，计算得到密文图像的NPCR和UACI均接近理想值，证明了该算法在加密过程中具有良好的敏感性．

表2 密文图像密匙敏感性

在解密过程中，采用同样的办法对密匙加以扰动，相应的测试结果如图7所示，从图7可以看出：加入扰动后该算法不能正确解出原始图像，同样说明了该算法具有良好的解密敏感性．

图7 解密密匙敏感性测试(解密图像)Fig.7 Sensitivity test for decryption key (decryption image)

3.7 信息熵

图像信息熵也可以反映图像灰度值的分布，一般来说，图像的灰度值分布越均匀，其信息熵就越大[24].其计算方法如下:

(21)

其中，L为像素的灰度级，p(xi)为灰度值xi出现的概率.表3给出了明文图像和密文图像的信息熵，从表3可以看出密文图像的信息熵与理论值(8)非常接近.表4给出了本算法的信息熵与现有图像加密方案得到的信息熵对比，从表4可以看出本算法的密文信息熵优于其他文献，说明本算法具有更好的加密效果．

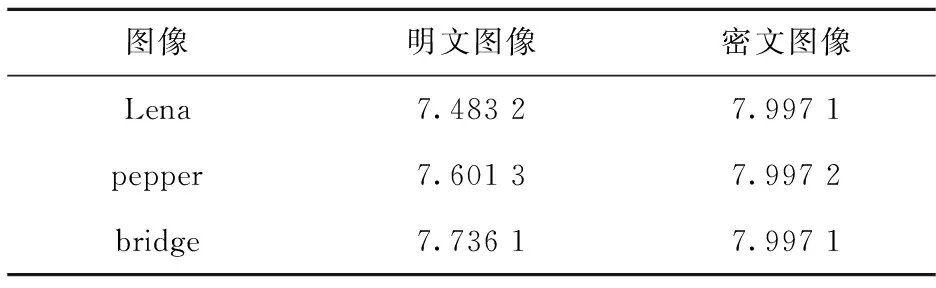
表3 明文图像与密文图像信息熵对比表

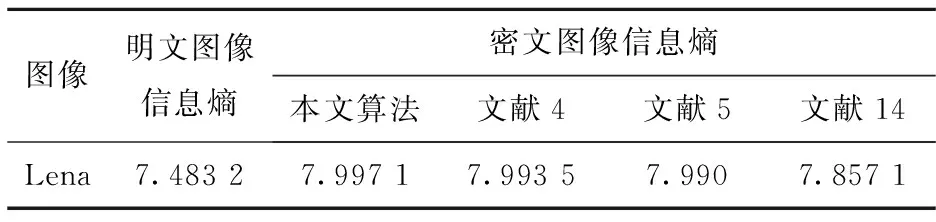
表4 信息熵对比分析表

3.8 抗剪裁分析

以Lena图像为例，对密文图像进行剪裁，即将其中部分像素值置成0.表5给出了经部分裁剪后的密文图像及其对应的解密图像.从表5可以看出密文图像经过不同程度的裁剪后解密，得到的密文图像虽然存在噪声，但并不影响图像的整体识别，说明本算法对图像各点置乱均匀，虽然剪切了一定面积的加密图像，解密后的图像都基本能辨清其轮廓.因为有置乱操作，被剪切的解密图像能均匀分散在整个图像上，因此该算法可以抵抗剪切和噪声污染的攻击．

表5 剪裁的密文图像及解密图像

4 结论

本文设计了一种5阶多涡卷混沌系统，分析了系统的基本动力学特性，包括平衡点、Lyapunov指数、Lyapunov维数等.同时将该系统应用于所提出的图像加密算法，并对加密系统进行了数值仿真，仿真结果验证了算法的有效性，因此，本文提出的数字图像加密系统在信息安全领域有潜在的应用价值．