基于LSTM网络鄱阳湖抚河流域径流模拟研究

姜淞川， 陆建忠*， 陈晓玲，2， 刘子旋

(1.武汉大学测绘遥感信息工程国家重点实验室， 武汉 430079；2.江西师范大学鄱阳湖湿地与流域研究教育部重点实验室， 南昌 330022)

对流域径流变化趋势的模拟与预测是水文学研究领域内的一个重要课题，它对于长期规划水资源的合理利用具有十分重要的指导意义[1].我国是洪涝灾害十分频繁的国家，它给人类生命、基础设施、农业、生态系统带来巨大损害[2-3].多时间尺度的径流模拟预报对于水资源可持续利用与规划具有非常重要的意义，然而径流变化的非线性和随机性等特点使得水文预报工作变得充满挑战，到目前还没有一个通用的模型能够在所有情况下对径流进行精确模拟.传统分布式径流预测模型主要基于研究区内复杂的气象物理过程，采取统计的方式建立预报方程，并结合经验指标对模型进行校准，因此多针对特定流域、特定预测尺度建立，推广及应用能力较差，难以对中小型地区进行建模，同时受限于对复杂物理过程知识的匮乏以及昂贵的计算成本，这种方法的预测效果并不理想[4-7].

深度学习(Deep Learning，DL)作为新一代人工神经网络，近年来在水资源和环境领域取得了长足的进展[8].多种常见的机器学习模型如人工神经网络(ANN)、决策树和随机森林(DT)、多层感知机(MLP)、支持向量机(SVM)等被广泛应用于水文预报和环境监测等问题的研究中[9].如Zhang等[10]采用基于深度学习的DBN结构和传统的反向传播神经网络对中国东海岸的赤潮现象进行了模拟预测，结果显示深度学习方法具有更好的泛化能力和更高的预测精度.Zhu等[11]采用卷积神经网络(CNN)和多层感知机混合模型进行了具有时空相关性的风速预测，这种组合模型的预报方法相较于单一机器学习模型取得了更好的模拟结果.Modaresi和Ebrahimi[12]采用4种数据驱动模型(ANN、GRNN、LS-SVR、KNN)对伊朗Karkheh大坝在线性和非线性两种情况下进行了月尺度的径流模拟，结果表明线性条件下ANN模拟效果最好而非线性条件下LS-SVR表现最优.崔东文等[13]对新疆伊犁河雅马渡站径流量预测过程中，基于多隐层BP神经网络模型，得到了比较理想的预报结果.目前存在的多种深度学习方法中，LSTM长短期记忆网络作为一种特殊的循环神经网络，能更好的处理具有长时依赖的水文数据.Kratzert等[14]在对大量流域进行实验的基础上探索了使用LSTM网络进行降雨-径流模拟的能力，实验表明LSTM在处理长时间序列数据上具有传统RNN不具有的优势，得出了在根据气象数据进行径流模拟的过程中应该使用LSTM而不是传统RNN的结论.Kratzert等[15]也探讨了LSTM模型在没有历史径流观测数据进行参数调优的情况下模拟径流的能力，结果表明基于LSTM建立的概化模型在大多数流域的表现都优于已建立的针对特定流域的水文模型.Zhang 等[16]采用LSTM网络进行污水的流量预测，结果表明LSTM方法在预测污水流动方面具有重要的应用价值.LSTM网络能够很好的处理时间序列数据，但是在空间数据处理上存在较多冗余.Shi等[17]基于这一问题提出了卷积LSTM网络模型，并成功应用于短时降雨的即时预报中.上述这些方法通过挖掘历史水文数据建立水文模型，相较于传统的统计预报模型提升了预报精度.鄱阳湖是我国最大的淡水湖，抚河流域作为鄱阳湖第二大子流域，是我国重要的粮食产地，也在调节长江水位、涵养水源、改善当地气候和维护周围地区生态平衡等方面起着巨大作用.然而关于鄱阳湖流域的水文预报工作却鲜有报道，采用深度学习方法进行径流模拟的工作更是少之又少.另外，为了测试深度学习径流模拟模型在新样本上的表现性能，往往需要将数据集划分为训练集与测试集，不同划分方法得到的模型评估结果往往不同，因此单一的数据划分方法得到的估计结果往往不够稳定可靠.

针对上述问题，本文首先基于Tensorflow开源模块在Python环境下编写代码构建模型，然后以气象站降雨数据和TRMM遥感降雨数据两种数据为驱动，分别进行日、月两种尺度的径流预报，对同一模型在不同驱动数据下的表现性能进行了比较评估，并对于驱动数据精度较差的情况下采用多重交叉验证的方法进行数据集划分，在一定程度上提高了模拟的精度，弥补了数据精度不足的缺陷，能够较好的分析出流域径流量的变化趋势.鄱阳湖抚河流域集水面积超过1万km2，降雨季节性变化大，流域水文气象站点众多，数据充沛，十分适合于水文预报工作的进行.同时鄱阳湖流域作为我国重要的粮食产地之一，采用水文预报方法进行防洪减灾具有十分重要的现实意义.本文在分析气象站和TRMM降雨数据的基础上，采用LSTM网络架构进行径流量的模拟与预报，以期为抚河流域水资源规划及防洪减灾、综合治理提供有效辅助决策手段和坚实理论依据.

1 研究区与数据获取

1.1 研究区概况

鄱阳湖作为我国最大的淡水湖，也是第二大的湖泊，位于25°～30°N，114°～118°E之间，南北跨度620 km，东西跨度490 km，流域面积约16万km2，主要有赣江、抚河、信江、饶河、修水五大支流，七个入湖口[18]，与中国江西省的行政区划重叠约97%.

抚河流域(图1)集水面积为15 811 km2，是五大支流中第二大的河流，位于26°30′～28°20′N、115°36′～117°10′E之间，地势南高北低，地貌以丘陵为主，山地和河谷平原交错分布.地处亚热带湿润季风性气候，年平均气温在17.2 ℃～18.9 ℃之间，年平均降雨量1 722 mm，降雨的时空分布不均，5月到7月降雨量约占全年的51%，春冬两季(10月到次年5月)降雨稀少[19].

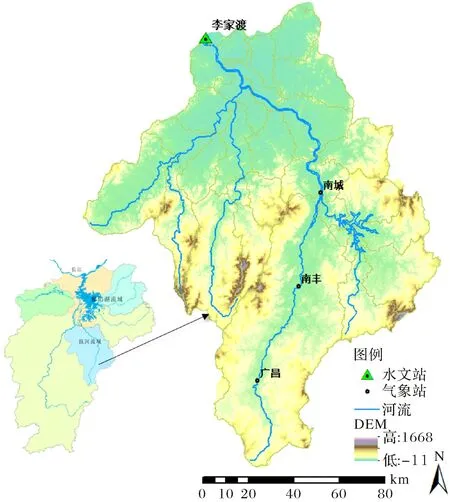
图1 鄱阳湖抚河流域及其水文站、气象站分布Fig.1 Map of Fuhe River Basin of Poyang Lake watershed with hydrological and meteorological stations

1.2 数据

本文使用的降雨数据分日、月两种尺度，日尺度的径流模拟实验采用从中国气象数据服务共享网站(http://data.cma.cn/)下载的鄱阳湖抚河流域内南城、南丰、广昌3个地面观测站从1960年1月1日至2009年12月31日共50 a 18 263 d的降水数据；月尺度的径流模拟实验采用1998年1月到2009年12月共144个月的TRMM数据.TRMM的全称为“Tropical Rainfall Measuring Mission Satellite”，它是由美国国家航天局(NASA)和日本航空探测局(JAXA)共同研发，专门对热带、亚热带的降雨进行测量的气象卫星[20].本实验构建的径流预测模型采用了3B43降雨数据作为驱动数据.3B43是一种网格形式的降雨数据，它融合了高精度的微波、红外数据以及地面雨量站数据，形成了一种以月为尺度的网格降雨数据，覆盖范围为50°S～50°N，空间分辨率为0.25°×0.25°[21].首先将下载到的HDF格网形式数据利用IDL语言转化为txt格式数据，然后将南城、南丰、广昌3个气象站所在的网格点对应的TRMM月降雨数据提取出来，对日尺度的地面观测降雨数据进行累加得到月尺度的地面实测数据，统一了时间空间尺度后，通过二者的比对实现对TRMM降雨数据的精度评估.本文使用的径流量数据是从李家渡水文站于1960年1月1日至2009年12月31日获取的日实测数据，通过将径流量逐月累加便能得到月尺度的径流实测数据.

收集到的降雨数据作为驱动数据输入到基于LSTM网络构建的降雨-径流模型当中进行计算，而收集到的径流量数据作为标签数据与通过模型计算得到的径流量模拟值进行比对得到损失函数(误差)，采用误差的反向传播算法使损失函数达到最小从而使模型参数得到优化，如此反复迭代便能得到最优的预报模型.

2 研究方法

2.1 模型设计与实现

Tensorflow是由Google公司的人工智能团队Google Brain开发和维护的一个用于数值计算的强大开源软件库，它十分适合用来进行机器学习方面的研究[22].降雨量(precipitation)是河流径流量最重要的影响因素.在一定的时间范围内，在河流流域的地形地貌以及土壤结构性质变化不大的情况下，可以忽略影响流域径流的其他过程参数，而直接建立降雨和径流的输入输出关系.本实验所使用的降雨数据包括地面气象站数据和TRMM遥感数据.气象站数据分布稀疏而精度较高，遥感数据分布均匀但精度较差，二者的互补可以减少由采样代表性、采样范围和频率以及数据获取模式不同所带来的差异性.同时采用位于鄱阳湖抚河干流下游的李家渡水文站实测的河流径流量作为对应于模型输入数据的标签数据，通过损失函数的计算来对模型进行训练.

从模拟的过程分，模型中的数据分为作为输入的驱动序列X，作为输出的模拟序列Y以及用作校准训练的标签实测序列O.由于LSTM网络的时序特征，在将序列数据输入到模型中之前需要将X、Y、O统一到同一个时间尺度下.由于降雨和径流的数据来源、单位量纲的不同，各种数据的值域范围可能会存在较大的差异，因此为了便于LSTM网络在训练过程中能够快速的使误差收敛获得最优解，需要对数据进行归一化处理.经过了时间尺度的统一和数据归一化处理后，便能构建输入向量，从而作为驱动数据输入循环网络模型.循环网络主要由多个LSTM层和两个全连接层组成(图3)，输入序列X进入循环网络处理得到输出序列Y，然后通过将输出序列Y与实测序列O的对比，基于反向传播优化参数的算法，最小化损失函数，然后重新将输入序列X输入到更新了模型参数后的循环网络，经过多次迭代直至损失函数小于某一设定值后停止迭代，模型训练结束.模型架构如图2所示.

循环体内部，输入序列Xn首先经过一个全连接层，流经多层LSTM网络，每层由多个LSTM神经元组成，隐藏层计算后的输出再作为输入进入到另一个全连接层，再经计算得到输出序列Yn，循环体(图2红框部分)内部结构如图3所示.

模型参数分为两部分(表1)：一部分为普通参数，包括循环体内部隐藏层各单元之间的连接权重和偏置、输入输出全连接层的权重和偏置，这部分参数由TensorFlow内置优化算法计算梯度并更新参数获得最优解；另外一部分为LSTM网络的超参数，主要有：

1) 隐藏层层数和每个隐藏层中LSTM神经元的个数，这两个参数确定了网络的基本结构，其中层数越多、每层神经元越多，模型参数越多，也就意味着训练过程越复杂，所需训练时间越多.

2) 最大时序截断长度time_step，由于LSTM在处理较长的序列数据时，在参数优化过程中的存在梯度消失或梯度爆炸的问题，因此在实际使用时需要设定一个最大时序截断长度.

3) 训练数据包大小batch_size，即一次输入模型中的样本个数，极限值为训练集样本总数.

4) 学习率learning_rate，学习率决定了模型训练时的收敛速度，学习率较大时，收敛速度较快但可能造成模型在局部最优解的附近摆动，学习率较少时，训练结果精度较高但是由于计算量变大，收敛速度较慢.

5) 迭代次数epoch，即模型将整个样本数据完整训练的次数，迭代次数的多少决定了模型是否会发生过拟合或者欠拟合现象.

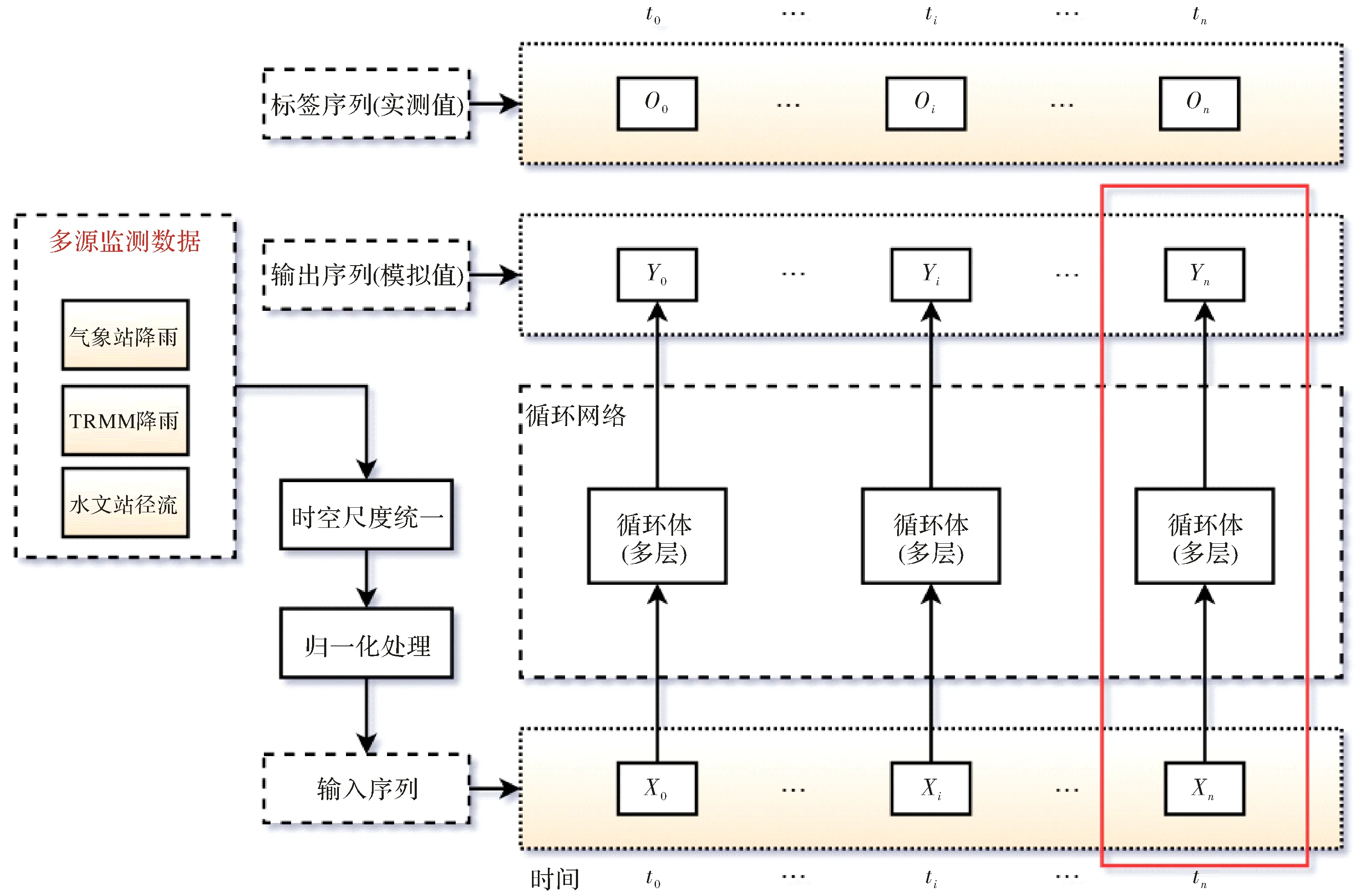
图2 基于LSTM网络的径流模拟模型Fig.2 Runoff simulation model based on LSTM network

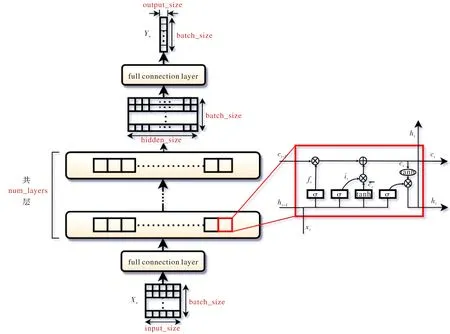
图3 循环网络内部结构Fig.3 The internal operation of recurrent network

参数类型参数名说明调参方式num_layers隐藏层层数全局超参数hidden_size单个隐藏层中神经元个数超参数time_steps最大时序截断长度经验调参batch_size训练数据包大小训练时超参数learning_rate学习率epoch迭代次数w_in,b_in输入全连接层参数普通参数w_rnn,b_rnn循环体隐藏层参数自动调参w_out,b_out输出全连接层参数

2.2 数据集划分方法

在日尺度的径流预测模拟实验中，由于河流径流量数据在年内具有相似的变化规律，因此直接将1960年1月1日—1989年12月31日共30 a数据作为训练集来对模型进行训练，1990年1月1日—2009年12月31日共20 a数据作为测试集来测试模型精度.

在月尺度的径流预测模拟实验中，由于数据量较小，为了提高模拟精度，采用“交叉验证法”对数据集进行划分，将1998年—2009年共12 a的数据集M等分为12个大小相同的互斥子集，即每年的数据作为一个子集.每次将1个子集作为测试集，其余11个子集作为训练集，共进行12次训练和测试，最终返回12个测试结果的均值.示意图如图4所示.

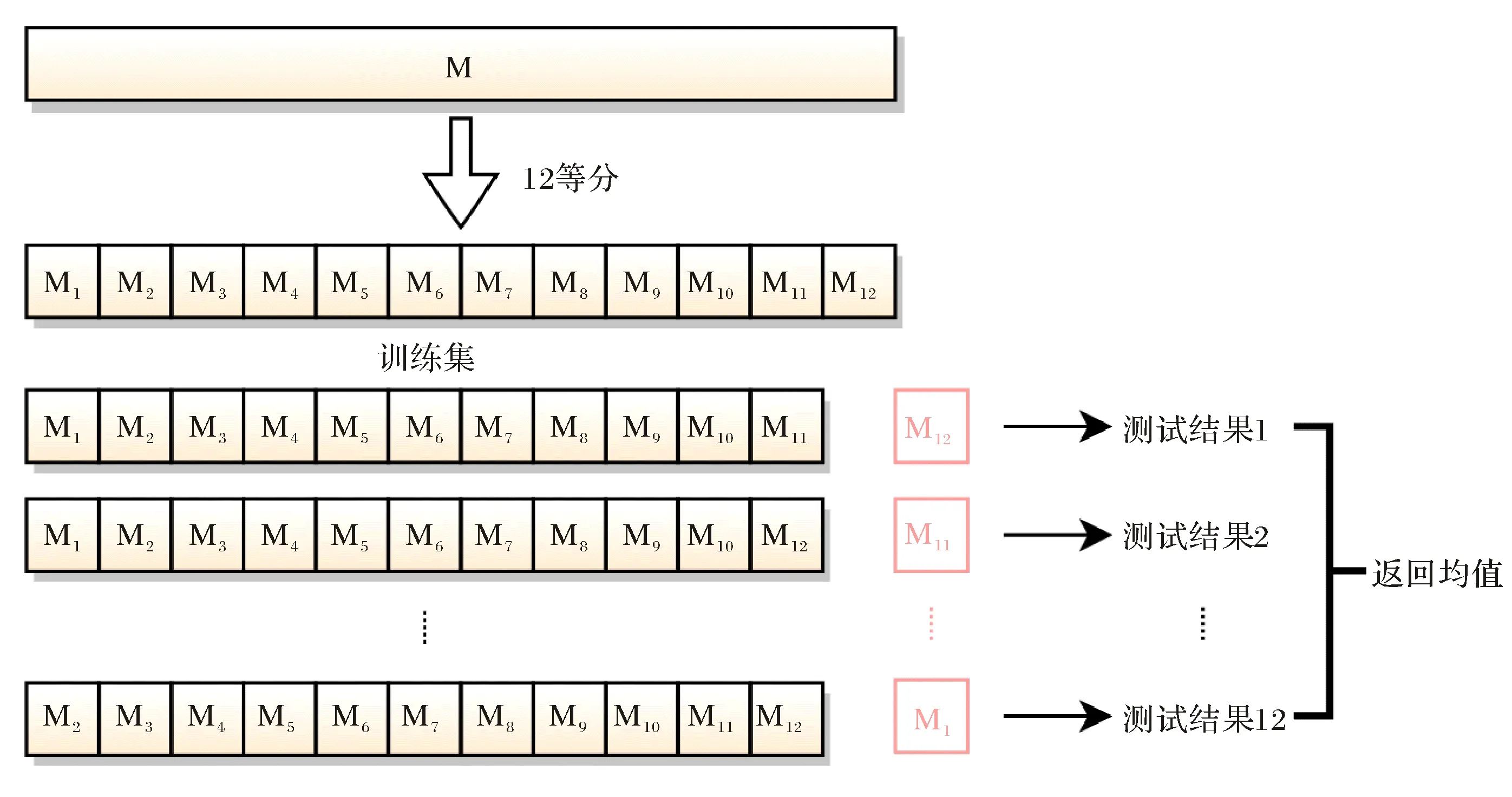
图4 月尺度径流模拟实验中采用“交叉验证法”对数据集进行划分Fig.4 The method of data set division in monthly runoff simulation: 12-fold cross validation

2.3 精度评价指标

为了定量描述模型的表现性能，采用相关系数R2、纳什系数NSE和百分比偏差Pbias来评定径流实测值与模拟值之间的“亲近性”，同时为了对TRMM遥感降雨数据进行精度验证，还加入了均方根误差RMSE来评定相同时空尺度下气象站数据和TRMM数据的相关性.表2详细介绍了本文所用精度指标的计算公式、取值范围以及最佳取值.

3 结果与分析

3.1 TRMM降雨数据精度验证

利用气象站观测的日降雨数据来对月尺度的TRMM遥感降雨数据进行精度验证，需要将两种数据统一到相同的时空尺度上.在时间尺度上通过对地面气象站的日降雨数据逐月累加便能将二者统一为月尺度数据；在空间上，直接将南城、南丰、广昌所在TRMM网格对应的降雨量作为与气象

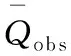
表2 R2、NSE、Pbias和RMSE计算公式、取值范围以及最佳取值(Qobsi为实测径流序列，

站数据相同空间尺度下的降雨数据.选择相关系数R2、均方根误差RMSE为评价指标，以TRMM降雨为横坐标，气象站月观测降雨为纵坐标，分别绘制3个气象站的散点图，并分别计算每个气象站的相关性指标(图5).从下图中可以看出，3个气象站的地面观测数据和TRMM数据的相关系数在0.88～0.94之间，表明两种数据的相关性较强.南丰气象站的TRMM数据和气象站数据的相关系数为0.88，在3个气象站中最低，表明TRMM数据在南丰位置的精度相较最低，广昌气象站相关系数达到0.94，表明TRMM在广昌精度最高；RMSE在30～50 mm之间，表明两种数据有一定的偏离，即每月大约相差30～50 mm.

3.2 基于气象站降雨的日径流预测

经过500次迭代训练后，使用TensorBoard对训练过程可视化，得到损失函数的收敛曲线如图6所示.

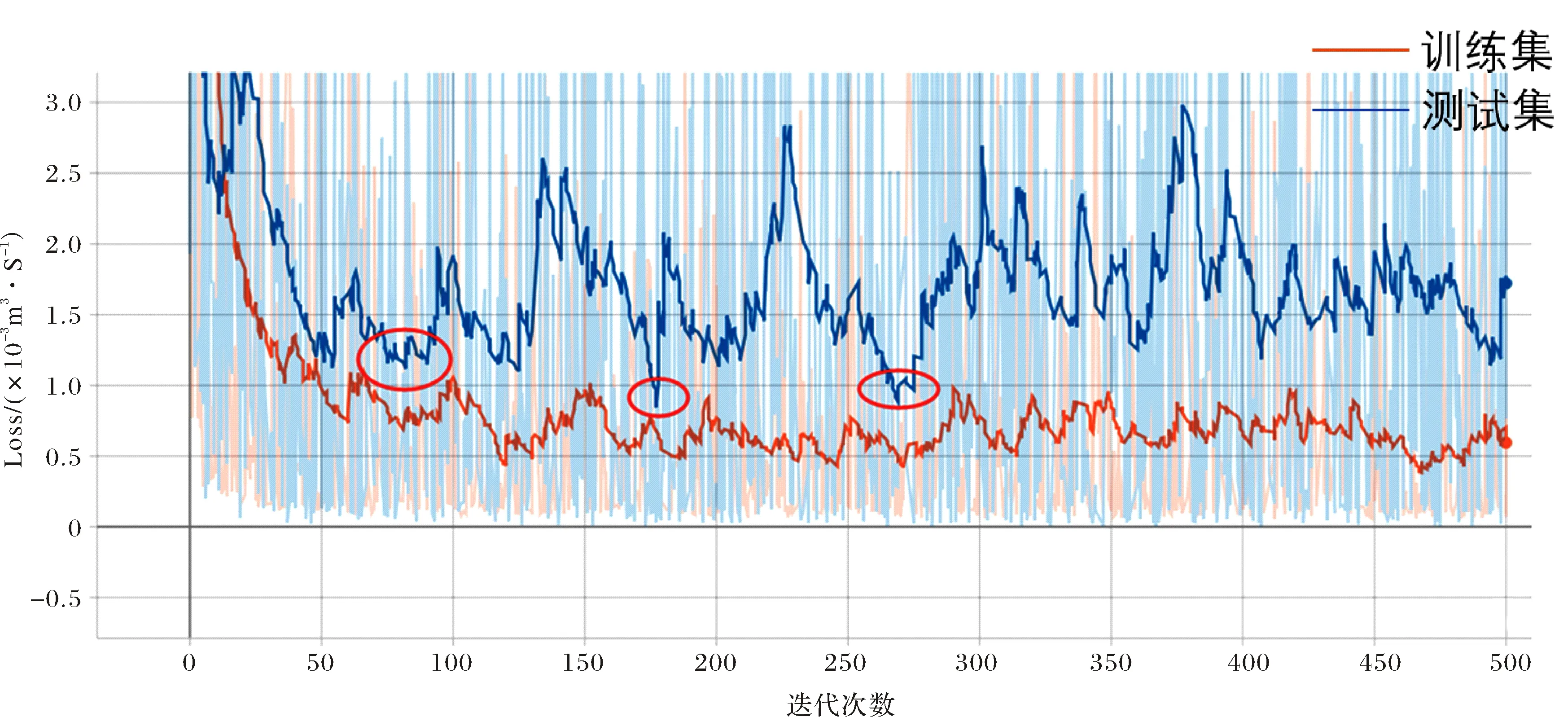
图6 日径流模拟模型500次迭代后得到的误差收敛曲线Fig.6 The error convergence curve derived from daily runoff simulation model after 500 iterations

可以发现在图6中红圈的范围内测试集的误差达到最小，因此分别将迭代次数为75、175和270的3个模型应用于训练集、测试集和整个数据集，计算得到模型评价指标(表3).可以发现无论在训练集还是测试集，径流模拟值与实测值之间的相关性指标(R2、NSE)均在0.92～0.96之间，百分比偏差均在±5%以内，模型表现非常好，其中迭代75次和175次偏差为正，模拟值整体偏低，迭代270次偏差为负，模拟值整体偏高.将训练175次的模型对数据集进行预测，将径流实测值与计算得到的径流模拟值按时间顺序绘制成图(图7～8)，整个数据集包含约18 000个数据点，由于数据量较大时间序列图并不能直观的描述模型的模拟结果，而使用流量历时曲线(Flow Duration Curve)可以更好的描述长持续时间数据集(≥10 a的每日数据集)模型的性能.以日均径流量为纵坐标，超过该径流量的累计天数为横坐标绘制得到迭代175次模型的流量历时曲线(图9)，图中可以发现无论训练集还是测试集，在较低径流量范围内(0～1 000 m3/s)，模拟值数据点大部分在实测值数据点的左边，说明相同的日均径流量，大于该值的模拟累计天数小于实际累计天数，反过来说也就是小于该值的模拟累计天数大于实际累积天数，说明径流模拟值整体偏低，而计算得到的偏差Pbias为正值(训练集4.97%，测试集2.22%)，同样表明模拟值偏低，二者结论相符.总的来说模拟值与实测值十分相近，模型模拟效果优秀.

表3 模型迭代75、175、270次日径流结果精度

3.3 基于TRMM降雨的月径流预测

通过依次将1998年—2009年中1 a的数据作为测试集，其余11 a数据作为训练集，共进行了12次的训练与测试，通过对比12次的训练与测试得到的径流实测值与预报值之间的精度评价指标，发现将2009年的数据作为测试集训练出来的模型表现最好，RMSE在训练集上为3 628.06 m3/s，是12种数据集划分方法中次最小的；测试集达到2 693.77 m3/s、全部数据集达到3 559.58 m3/s，均是所有12个测试结果中最小的， 因此将该划分方式的训练结果单独取出，作为本实验的径流预测结果.利用Tensorboard对训练过程可视化，得到误

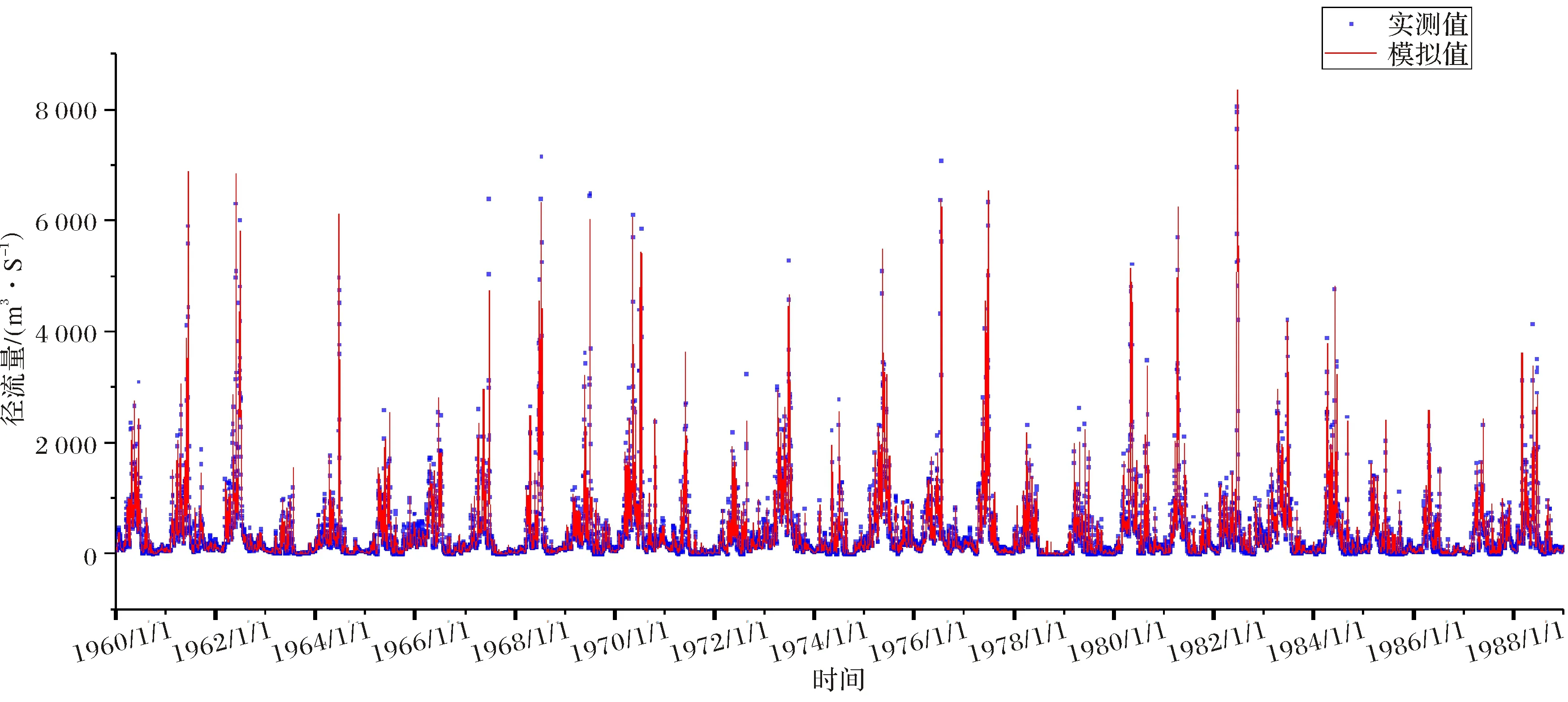
图7 迭代175次训练集的日径流模拟结果Fig.7 Comparison of simulated and observed runoff in training set derived from daily runoff model after 175 iterations

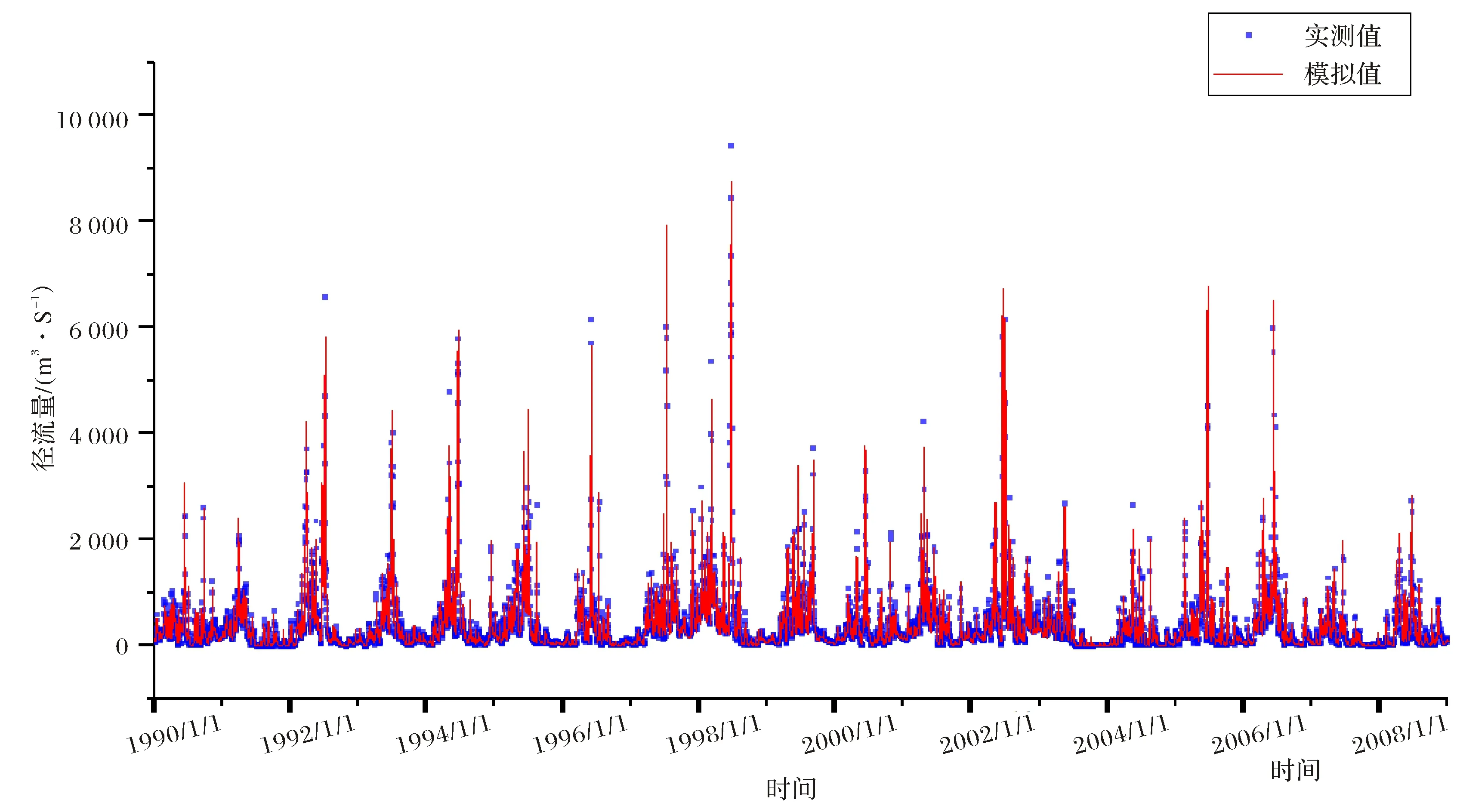
图8 迭代175次测试集的日径流模拟结果Fig.8 Comparison of simulated and observed runoff in test set derived from daily runoff model after 175 iterations

差收敛曲线(图10)，发现在迭代3 100次左右测试集误差达到最小，将迭代3 100次训练出的模型应用于训练集、测试集和整个数据集，得到的精度评价指标及预报曲线如表4、图11.从表4中可以看出，模型在训练集的相关性均在0.9以上，偏差在±5%以内，模拟效果非常好；测试集R2和NSE分别为0.81和0.74，模拟效果良好；偏差大于±15%，模拟效果很差，原因可能有两点，一是因为TRMM降雨数据本身的精度较低，另一个是由于测试集样本数非常少，仅有12个样本点，因此评价指标的偶然性很大.从整个数据集来看，相关性大于0.9，偏差小于±5%，模型整体表现非常好.从图11中可以看出，模型对于径流峰值的模拟偏低，整体模拟值与实测值吻合的较好.

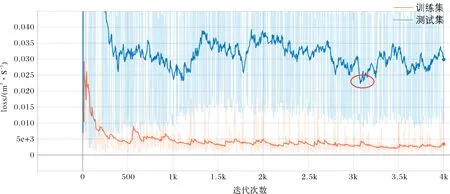
图10 月径流模拟模型4 000次迭代后得到的误差收敛曲线Fig.10 The error convergence curve derived from monthly runoff simulation model after 4 000 iterations

评价指标训练集测试集整个数据集R20.930.810.92NSE0.910.740.91Pbias/%1.3618.240.43

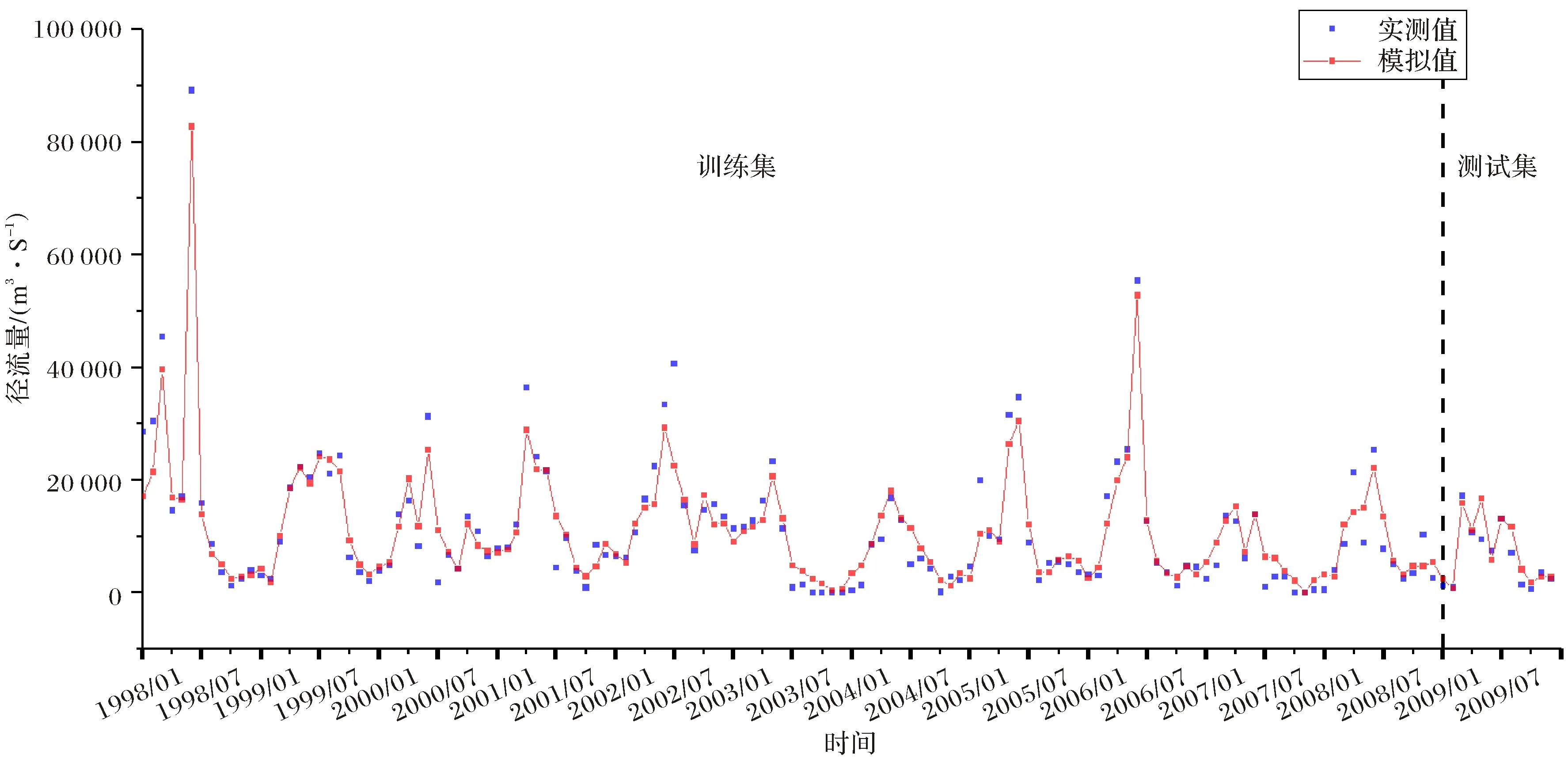
图11 月径流模拟模型迭代3 100次模拟结果Fig.11 Comparison of simulated and observed runoff derived from monthly runoff simulation model after 3 100 iterations

4 讨论

在模型精度评价方面，Moriasi等[23]在对大量水文预报模型研究的基础上，针对模型评价指标和模型表现性能评价提出了一个统一的评价标准(表5)，本实验的日径流模拟值与实测值之间的相关性指标(R2、NSE)均在0.92～0.96之间，百分比偏差均在±5%以内，模型表现非常好；月径流模拟值与实测值从整个数据集来看，相关性大于0.9，偏差小于±5%，模型整体表现非常好.在与现有研究成果对比方面，李云良等[24]采用分布式水文模型WATLAC为模拟工具对鄱阳湖各子流域进行了径流模拟.朱漫莉[25]等采用系统动力学(SD)方法构建了鄱阳湖各流域系统中各要素的物理结构和关系，从而对径流进行了模拟.表6汇总列出了近几年研究中各模型在鄱阳湖抚河流域的径流模拟精度及其与本文LSTM的模型对比.由此可以看出本文利用长时间序列数据训练出来的LSTM径流模拟模型在鄱阳湖抚河流域的模拟表现更好，总体精度更高.

表5 水文预报模型评价指标取值范围及其对应的模型性能评价标准

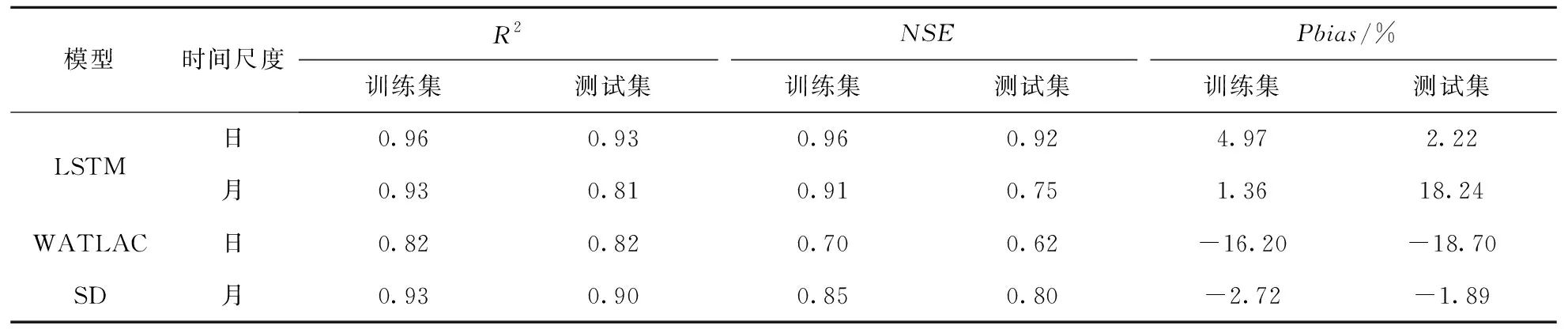
表6 鄱阳湖抚河流域各模型径流模拟精度

5 结论

长时间尺度(如年、季、月)径流预报对水库调度、河流输沙、水力发电和灌溉管理等具有重要的指导意义；实时(日、小时)径流预报则对于洪水预报、预警工作的进行有着重要意义.本文基于LSTM长短期记忆网络，以地面气象站观测的日尺度降雨数据和TRMM月尺度遥感降雨数据为驱动数据，对鄱阳湖抚河流域的径流量进行了模拟预报.以相关系数R2、纳什系数NSE和百分比偏差Pbias作为精度评价指标对模型性能进行评价，其中日、月两种尺度的R2、NSE在整个数据集上均大于0.9，Pbias均小于±5%，根据Moriasi提出的评价标准来看均达到了非常好的程度.日径流模拟模型样本数充足，直接采用按比例的方法对数据集进行划分，结果显示训练集和测试集的模型表现均非常好；月径流模拟模型由于样本数目较少，在测试集仅有12个样本点的情况下模型表现较差，但模型在整个数据集上的表现依然非常好，因此在数据集样本容量较小的情况下采用交叉验证法对数据集进行划分能够提高模拟精度.上述实验说明两种尺度的LSTM模型与传统分布式水文预报模型相比计算成本更低、计算量更小、精度更高.然而，本实验仅将降雨数据作为模型的影响因子而实际上径流量的影响因素众多，在后续的研究中可以将卷积神经网络与LSTM网络相结合，考虑将流域内的下垫面信息(如土地利用状况、土壤特征、地形要素等)纳入模型当中进行综合评判，从而能够充分发挥两种网络各自的特点，实现优势互补.