混凝土工字梁偏心受压应力场超声测试

汤 真

(重庆交通大学，重庆 400074)

0 前 言

20世纪30年代，人们开始研究混凝土无损检测方法，80年代，美国学者Mary Sansalone利用机械波反射法进行无损检测，近年来，测试内容也由强度推定、内部缺陷探测等扩展到混凝土结构应力范畴，2012年，宋丽莉等[1]对水泥和岩石样品开展散射波试验研究，证明多次散射波形成的尾波比直达波对介质性质变化更为敏感，2018年，黎志谋[2]开展了超声尾波对混凝土梁三点弯曲应力场超声测试，利用泰勒展开式，建立了幅值一阶变化系数与应力变化近似线性曲线。

本文制定了混凝土工字梁偏心受压超声尾波应力测试方案，以奇异值分解为基础理论，建立了超声尾波波形的幅值特征向量与混凝土结构荷载等级关系曲线。

1 试验方案制定

本方案对混凝土工字梁空载及20个荷载的偏心压力作用下进行超声测试，设计好荷载取值范围及施加荷载的具体位置，利用Midas Civil建立试验加载模型提取出相应的应力计算值，由RSM-SY5(T)型非金属超声波检测仪发射超声脉冲信号，通过接收多次散射波形成的尾波记录及保存数据。

1.1 试件设计

本次试验采用的梁体构件为钢筋混凝土工字型梁，跨径2 m，整体梁高45 cm，其中翼缘板宽30 cm，翼缘板高10 cm，腹板宽10 cm，腹板高25 cm。纵向钢筋和箍筋均采用直径为10 mm的HPB300级钢筋。

1.2 超声测试装置及加载系统

1.2.1 超声测试装置

超声测试装置由RSM-SY5(T)型非金属超声波检测仪和换能器组成，平面换能器中心频率50 kHz，直径为4 cm，布置方式为一发双收，换能器布设位置如图1所示。

1.2.2 试验加载系统

利用Midas Civil对不同荷载等级下工字型梁体的应力大小进行计算，提取出相应的应力计算值，表1所示。

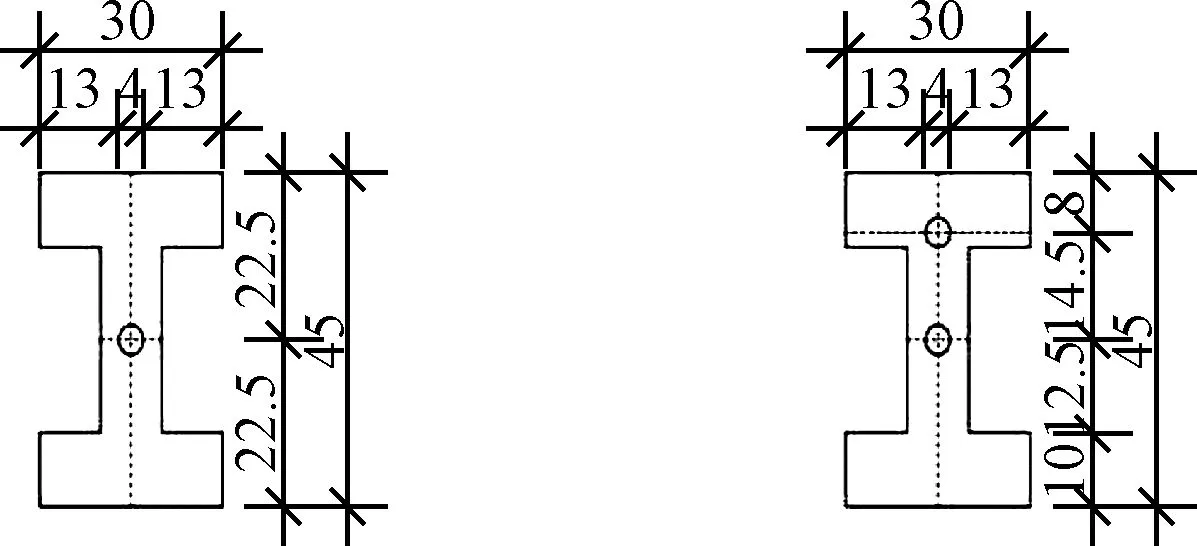
图1 换能器布设位置示意图(单位：cm)

表1 钢筋混凝土工字型梁部分荷载等级下的应力值

加载方式采用单级加载，采用千斤顶对混凝土工字梁端面施加偏心压力，千斤顶力作用点距梁体侧表面形心轴下方7.5 cm。为保持千斤顶对梁体所施加的压力不回缩并实时监控施加偏心压力，在梁体两侧钢筋贴应变片并配套应变检测仪，加载系统如图2所示。

图2 加载系统示意图

1.2.3 试验流程

首先对超声测试仪器进行30 min左右的预热，然后利用千斤顶对梁体进行偏心加载。每天进行一次完整混凝土工字梁偏心加载试验，每次完整试验共7组超声测试，每组测试共21个荷载状态(含自重)，荷载范围(1～20 kN)，每一级荷载测试将记录超声波形11条，共进行5次完整试验，如图3所示。

图3 现场加载测试示意图

2 试验数据处理与分析

由于本试验有2处接收端，故偏心加载试验数据可构成7×21×11×1 024×2的五维矩阵，为建立了超声尾波波形幅值特征向量与荷载等级间关系曲线，在数据分析中以偏心荷载等级为自变量，把数据进行平均处理，原始波形进行奇异值分解，利用SVD矩阵性质建立幅值与荷载等级关系，实现采用幅值特征向量来表征荷载等级的数据处理目标。

2.1 数据预处理

选用任一端一次完整试验测试数据得到7×21×11×1 024的4维矩阵W′，将一次采集数据进行预处理，物理意义容易理解每一级荷载有一个波形，将W矩阵按11次重复移点测试平均为一次，每一天重复测试8组平均为1组，得到21×1 024的二维矩阵。

由于每次超声测试采集到的波形能量不尽相同，波形数据不具备可比性，为了使波形数据各类指标位于同一数量级上，对其进行了能量归一化处理,具体过程如下:一条完整的波形Wj由1 024个点构成,Xj为幅值。

Wj=Wj(x1,x2……x1024)

(1)

波性能量：

(2)

波形能量归一化处理：

(3)

2.2 基于奇异值分解的数据处理

数据经预处理后得到21×1 024二维矩阵W，矩阵W为实数矩阵，W∈Rm×n，则一定存在正交矩阵U∈Rm×m，正交矩阵V∈Rn×n和对角矩阵Σ∈Rm×n，本文中m=1024，n=21，进行奇异值分解矩阵W可表示为[3]：

W=UΣVT

(4)

Σ可表示如下：

(5)

式中，0为零矩阵；p为min(m,n)；σp为矩阵W的奇异值，且σ1≥σ2≥…≥σp≥0。

正交矩阵U与VT满足：

UHU=Em,m

(6)

(VT)HVT=En,n

(7)

式中，UH、(VT)H分别为U、VT的共轭转置为Em,m、En,n分别为m阶、n阶单位矩阵。

为建立不同荷载等级下超声尾波波形数据特征值与荷载等级间的函数关系，设存在特征向量wx，使其与奇异值分解后矩阵相乘等于W与线性向量[ax+b]相乘可表示为：

wxUΣVT=[ax+b]W

(8)

式(8)左右两侧同时右乘：

wxEm,mEm,nEn,n=[ax+b]W(VT)HΣ-1UH

(9)

2.3 数据处理结果与分析

由于矩阵W′经过多次平均处理，为向工程实际过渡，需要确保数据在组内、组间的稳定性、重复性，下面考察各组内及组间数据结果，逐一进行分析。

1)组内数据结果分析。从组内角度考察各天的测试数据：①单天测试数据构成的11×1 024×7×21 四维数据矩阵；②7 个 11×1 024×21 的三维数据矩阵；③进行能量归一化处理使得波形数据各类指标位于同一数量级上；④采用基于奇异值分解的数据处理方式求取单组组内 11 条波形各自的幅值特征向量Wx；⑤建立幅值特征向量与荷载等级间的近似线性关系曲线。

基于奇异值分解原理求取不同组数下组内 11 条波形的幅值特征向量，建立了幅值特征向量与荷载等级间线性关系，如图4所示：

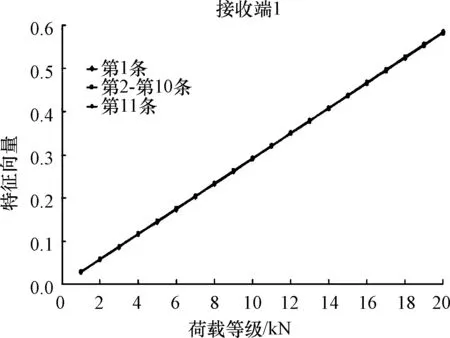
图4 组内数据特征向量与不同荷载等级间的关系曲线

接收端1、接收端2单组组内11条波形的特征向量Wx与荷载等级间呈现近似线性关系，并且特征向量Wx的离散程度极小。

2)组间数据结果分析。单天测试数据构成的11×1 024×7×21四维数据矩阵按测试组数的不同拆分为7个11×1 024×21的三维数据矩阵，每个三维数据矩阵代表单组测试过程中采集到的波形数据，首先求取11条波形的平均，可将7个三维数据矩阵整合成7个21×1 024的二维矩阵。

进行能量归一化处理使得波形数据各类指标位于同一数量级上，以单天整体测试数据所构成的二维矩阵W作为开展奇异值分解的基准，分别带入单组测试数据，求解出各组测试数据在不同荷载等级下的特征向量，建立不同组数据的幅值特征向量与荷载等级间的近似线性关系曲线，如图5所示。

图5 各组特征向量与不同荷载等级间的关系曲线

接收端各组测试数据任然存在特征向量Wx与荷载等级间近似线性关系曲线，但同一荷载等级下各组测试数据的特征向量Wx上下位置随机分布，未出现按加载测试先后顺序分布。剔除第一组(黑色线)，其余六组测试数据的特征向量Wx间离散程度较小，能达到利用特征向量Wx来识别荷载等级的数据处理目标。

第一组测试数据特征向量Wx明显偏离于其余六组，主要考虑两方面，①仪器设备考虑预热及梁体本身对荷载反应过程记忆了之前的受力历史拥有了“凯撒效应”；②耦合剂与梁体耦合状态稳定时间。

3 结 论

对偏心受压应力场下构件及混凝土梁开展了超声尾波试验，基于奇异值分解后的超声尾波波形幅值特征向量来表征偏心荷载等级的结构测试模型，建立了超声尾波波形幅值特征向量与荷载等级间的近似线性关系曲线。

从组内的角度对单天测试数据展开处理及分析，单组组内 11条波形数据的幅值特征向量与荷载等级间呈现出近似线性关系，并且不同荷载等级下单组组内 11 条波形数据的幅值特征向量离散程度极小；从组间的角度对单天测试数据展开处理及分析，线性关系明显，虽然不同组的波形幅值特征向量间出现了随机的偏移，但识别荷载等级仍然有效。

[ID:009085]