基于正交试验法的龙门式折弯机的轻量化设计
林冠屹 管殿柱 张开拓 宋占杰


摘要: 针对某公司设计的一款龙门式折弯机,本文在其正式投入生产与工作之前进行计算机模拟分析,在验证设计方案可行性的同时进行轻量化设计。首先通过Solid Works对折弯机进行三维建模,模型简化后导入ANSYS Workbench15.0,通过对主要受力部位施加载荷与压强,划分网格,在最大应力小于材料屈服极限值,即保证材料性能的前提下,得出整体变形的分析结果。根据折弯机变形情况,设计结构优化方案,将工作台侧板厚度、工作台支撑板厚度、工作台顶板厚度、折弯机拉杆直径与上压板筋板厚度5个对分析结果影响显著的结构参数添加进来,进行正交试验,根据试验组号重新建模进行有限元分析。以折弯机质量最轻为目标函数,设置状态变量及尺寸变量的边界条件,使用SPSS统计分析得出系数,建立折弯机轻量化数学模型,运用Matlab优化工具箱进行求解,将各个参数圆整后重新建模并进行有限元分析,最终使折弯机整机质量减轻了3.36%,同时保证了折弯机的工作性能,优化效果显著。该研究具有一定的实际应用价值。
关键词: 正交试验法; 轻量化设计; 龙门式折弯机; ANSYS Workbench; 有限元分析
中图分类号: TH122 文献标识码: A
收稿日期: 2019-09-30; 修回日期: 2019-11-15
作者简介: 林冠屹(1993-),男,硕士研究生,主要研究方向为数字化设计及虚拟样机技术。
通信作者: 管殿柱(1969-),男,硕士,教授,主要研究方向为数字化设计及虚拟样机技术。Email: gdz_zero@126.com
折弯机作为钣金加工业的一种重要母机,广泛应用于钣金弯曲成型加工,在汽车、金属结构、电子、简述装潢等领域广泛应用[1-4]。折弯机的工作原理是将作用力作用于压板或滑块上,使其连续上下运动,将固定工作台上的板料或工件强制折弯成特定形状。折弯机的驱动方式分为气动式、机械式和液压式,其中应用最广泛的是液压式折弯机[5]。目前,市场上最常见的是C型折弯机,其结构设计简单,易于制造,但只能对某种截面形状的材料进行折弯,且折弯时喉口处存在应力过大的问题[6]。利用传统设计方法自主设计的龙门式液压折弯机,虽然具有较大的安全系数,但其结构设计比较笨重,增加了生产成本,需要进行轻量化设计[7]。基于此,本文以某公司设计的一款龙门式折弯机为模型,在对模型进行静力学分析的基础上,设置目标函数和边界条件,采用正交试验方法,运用Matlab软件进行求解,进而得到折弯机轻量化结构,最终使折弯机整机质量减轻了3.36%,优化效果明显。该研究具有一定的实际应用价值。
1 有限元分析
1.1 折彎机三维模型分析
本文所用龙门式折弯机使用单缸压力为8 000 kN的液压缸为动力元件,设计的最大工作压力为80 000 kN。折弯机工作台和四周的立柱及上部的油缸机架构成了折弯机外部结构,起固定、支撑及连接作用[8]。超大型折弯机的固定方式比较特殊,工作台通过地脚螺栓与地面连接固定,工作台底部嵌入地下,看作全约束。工作台与油缸机架通过4个立柱连接,每个立柱内部有4根拉杆,为折弯机工作提供有效拉力,有效防止折弯机机身形变位移过大。底模与工作台顶板固定连接,上压板与液压缸固定连接,通过控制液压缸的进给量将置于上压板与底模之间的板材折弯成不同角度。龙门式折弯机三维模型示意图如图1所示。
1.2 折弯机有限元模型分析
对折弯机模型进行有限元分析时,需要对折弯机的计算机辅助设计(computer aided design,CAD)模型进行适当简化和修改,否则在转换为计算机辅助求解(computer aided engineering,CAE)模型时可能会出现某些问题[9]。针对龙门式折弯机结构的特点,对其模型作如下简化。删除部分与折弯机强度和刚度无关的螺纹及螺纹孔等结构,将工作台底部约束视为固定约束,将焊接连接强度视为与整体材料相同,去除对整体受力影响较小的部件。在不影响分析误差的前提下进行简化,确保分析的正常进行。
对模型进行网格划分时应遵循均匀、应力区粗划、应力梯度细化的原则[10-11],合理的网格划分可提高有限元分析结果的准确性,但网格数量的增加会加大计算机的运算负担,从而增加运算时间。本文对折弯机模型的网格划分采用四面体网格划分的方法,有效避免以上问题。网格划分完成后,得到模型单元数为129 693,节点数为550 029。
1.3 折弯机材料及参数设置
龙门式折弯机主体机身材料为Q235,钢板采用焊接方式连接,折弯机拉杆材料采用40CrMo,经查阅手册确定其材料参数,材料基本参数如表1所示。
折弯机工作时,所受载荷实际上随时间发生线性变化,在进行静力学分析时,仅考虑满载时的结构受力情况,为保证其最大受力极限工况下的安全性能,取折弯机满载时的工况为分析场景,根据初试设计要求,在折弯机工作时,由固定在上机架上的10个公称力为8 000 kN的液压缸向下推动压块完成板材折弯[12],上机架承受液压缸底部向上的反作用力F为
F=800 000 kg×9.8 N/kg=7.84×106 N
根据该龙门型折弯机的实际技术参数,分别计算液压缸所受压强P1,凸台所受压强P2,压板所受压强P3,工作台所受压强P4。
根据压强计算公式
P=F/A(1)
可得液压缸所受压强为
P1=7.84×106 N565 072.34 mm2≈13.874 MPa
凸台压强为
P2=7.84×106 N501 976.82 mm2≈15.618 MPa
压板压强为
P3=7.84×107 N25×121 500 mm2≈25.811 MPa
工作台压强为
P4=7.84×107 N9 500 000 mm2≈8.253 MPa
根据拉杆预紧力公式
F0≤0.5~0.6σsA1(2)
式中,σs为螺栓材料屈服极限,MPa;A1为螺栓危险截面面积,A1≈(πd21/4)mm2。
分析验证结果表明,预紧力系数的值在0.05~0.5之间时,应力随系数的增加而增加。考虑到折弯机的震动,建议以拉紧螺杆公称力的1%~5%倍在装配时进行预紧[13],拉杆直径d=200 mm,取预紧力系数为1%,通过计算得拉杆预紧力约为292 000 N。
1.4 折弯机静力学分析结果
将折弯机模型导入ANSYS Workbench模块,参数设置完成后,进行静力学分析,得到龙门式折弯机机身分析云图,折弯机静力学分析云图如图2所示。由图2可以看出,折弯机上压板部分在额定工作载荷下变形量最大,最大值为5.03 mm;工作台固定板与支撑板连接处有应力集中现象,应力最大值为209.72 MPa,符合实际工况,但机身质量较大,需要进一步优化。
2 正交试验
2.1 正交试验设计
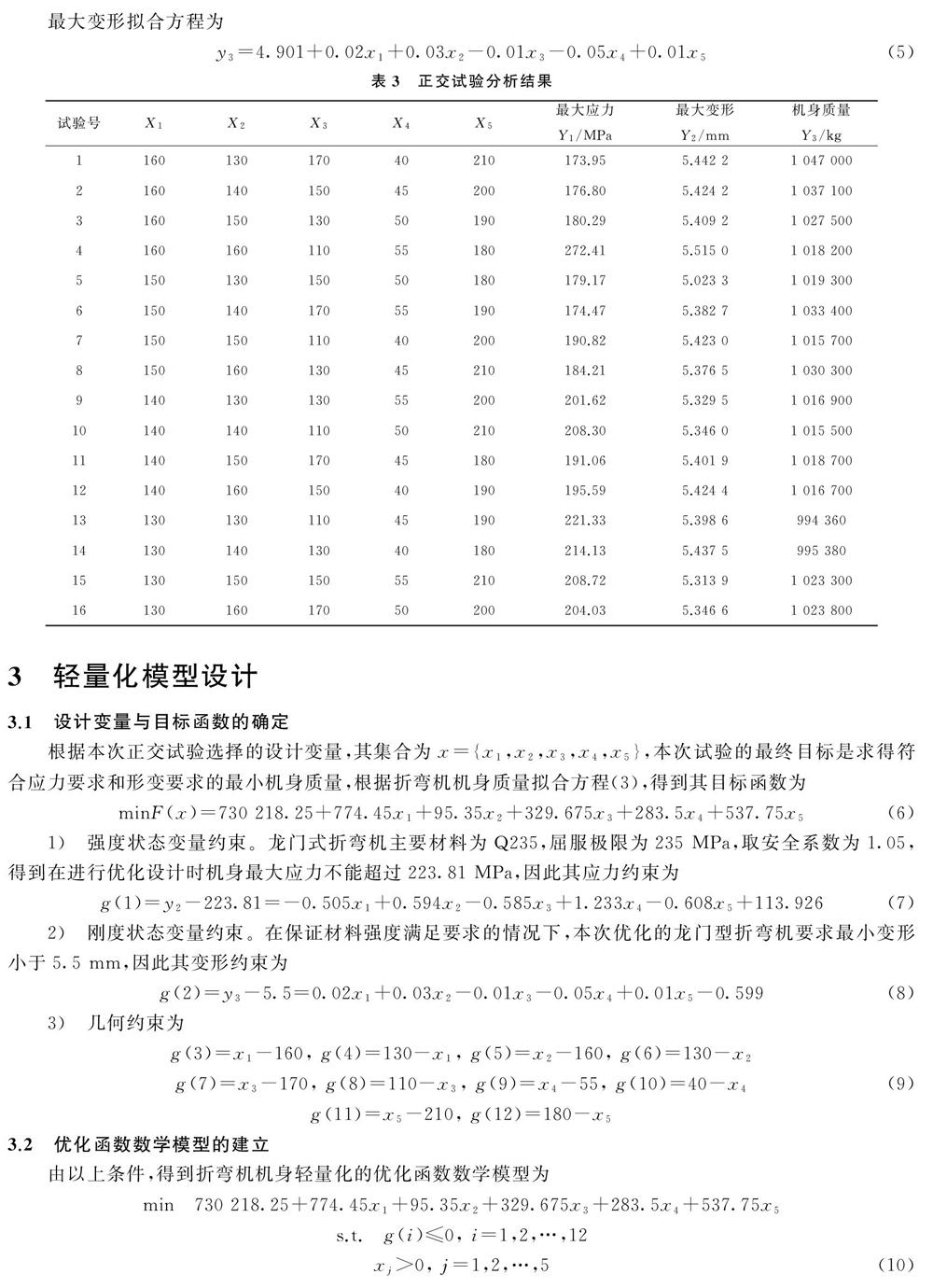
正交试验设计方法利用正交性挑选具有代表性的参数作为变量,建立试验因素水平表进行组合试验,通过正交试验法可有效减少了试验次数[14-16]。由折弯机静力学分析可知,工作台侧板厚度X1、工作台支撑板厚度X2、工作台顶板厚度X3的选取直接影响折弯机变形和应力,同时上压板筋板厚度X4、拉杆直径X5取值的不同也会造成机身应力和最大变形的变化,对其选取合理的厚度至关重要。因此,使用X1~X5这5个参数进行正交试验,试验因素水平表如表2所示。选用L16(45)型正交表[17],使用ANSYS Workbench依次对16种结构进行静力学分析,正交试验分析结果如表3所示。
2.2 回归函数的构造
通过正交试验,得到不同尺寸模型对应的最大应力、最大变形和机身质量数据,设置因变量与自变量分别得到基于最小二乘法的最大应力、最大变形、机身质量的线性回归系数,将表3的数据输入SPSS18.0中[18],得到各线性拟合方程。
机身质量拟合方程为
y1=730 218.25+774.45x1+95.35x2+329.675x3+283.5x4+537.75x5(3)
最大应力拟合方程为
y2=327.566-0.505x1+0.594x2-0.585x3+1.233x4-0.608x5(4)
最大变形拟合方程为
y3=4.901+0.02x1+0.03x2-0.01x3-0.05x4+0.01x5(5)
3 轻量化模型设计
3.1 设计变量与目标函数的确定
根据本次正交试验选择的设计变量,其集合为x={x1,x2,x3,x4,x5},本次试验的最终目标是求得符合应力要求和形变要求的最小机身质量,根据折弯机机身质量拟合方程(3),得到其目标函数为
minF(x)=730 218.25+774.45x1+95.35x2+329.675x3+283.5x4+537.75x5(6)
1) 强度状态变量约束。龙门式折弯机主要材料为Q235,屈服极限为235 MPa,取安全系数为1.05,得到在进行优化设计时机身最大应力不能超过223.81 MPa,因此其应力约束为
g(1)=y2-223.81=-0.505x1+0.594x2-0.585x3+1.233x4-0.608x5+113.926(7)
2) 刚度状态变量约束。在保证材料强度满足要求的情况下,本次優化的龙门型折弯机要求最小变形小于5.5 mm,因此其变形约束为
g(2)=y3-5.5=0.02x1+0.03x2-0.01x3-0.05x4+0.01x5-0.599(8)
3) 几何约束为
g(3)=x1-160, g(4)=130-x1, g(5)=x2-160, g(6)=130-x2
g(7)=x3-170, g(8)=110-x3, g(9)=x4-55, g(10)=40-x4(9)
g(11)=x5-210, g(12)=180-x5
3.2 优化函数数学模型的建立
由以上条件,得到折弯机机身轻量化的优化函数数学模型为
min 730 218.25+774.45x1+95.35x2+329.675x3+283.5x4+537.75x5
s.t. g(i)≤0, i=1,2,…,12xj>0, j=1,2,…,5(10)
3.3 轻量化计算
为满足轻量化要求,根据KuhnTucker条件[19],得
ΔfX-∑12i=1ωiΔSX=0ωiSX=0, i=1,2,…,12; ωi≥0, i=1,2,…,12(11)
利用Matlab软件进行数学模型计算,得出其计算结果,圆整后选用X1=130 mm,X2=132 mm,X3=112 mm,X4=42 mm,X5=181 mm。
4 优化结果分析
按照优化圆整后的尺寸修改模型,进行有限元静力学分析,得到优化后的龙门式折弯机分析结果云图如图3所示。
由图3可以看出,该参数下的折弯机模型應力符合材料屈服强度的要求,变形量增加较小,机身质量减小。将折弯机轻量化设计前后的有限元分析结果进行对比,计算得优化结果对比表如表4所示。
5 结束语
本文通过对折弯机进行有限元分析,确定对折弯机性能影响较大的结构参数,提出正交试验的轻量化设计思路,设置5个变量作为正交试验参数,得到机身参数的回归模型,建立优化数学模型,对折弯机进行了轻量化设计。由分析设计结果可以看出,优化之后的模型质量减轻3.36%,应力、变形量有一定增加,符合设计要求,达到了轻量化的目的,降低了企业的生产成本。该设计将多个设计变量作为优化参数,得到轻量化结果较为显著,该方法普遍适用于机械设备的轻量化设计。
参考文献:
[1] 顾忠新, 胡智明. 基于ANSYS折弯机机架的有限元分析[J]. 锻压装备与制造技术, 2014, 49(1): 26-28.
[2] 周欢, 王丽丽, 王金荣, 等. 折弯机液压补偿装置对工作台挠度曲线的影响分析与优化[J]. 机床与液压, 2016, 44(20): 40-43.
[3] 周婉, 钱怡, 平东良. 折弯机的有限元建模及强度和变形分析[J]. 江南大学学报: 自然科学版, 2014, 13(2): 179-183.
[4] 田万英, 高建和, 潘志华. 折弯机压力不均匀分布研究[J]. 锻压装备与制造技术, 2011, 46(6): 44-47.
[5] 范宏才. 现代锻压机械[M]. 北京: 机械工业出版社, 1994.
[6] 严庆光, 李明哲, 蔡中义. C型号多点成形压机机架结构有限元分析和优化设计[J]. 锻压机械, 2002, 37(3): 44-47.
[7] 翟庆波, 苏兆婧. 轻量化设计在工程机械中的应用[J]. 设计, 2016(17): 120-121.
[8] 崔蓬勃. 500吨折弯机的结构与优化[D]. 青岛: 青岛大学, 2018.
[9] 刘祥. WF67Y-160/3200数控折弯机有限元分析[J]. 科技与生活, 2012 (21): 170-171.
[10] 胡亚民, 夏华, 陈善民, 等. 我国弯曲成形技术的发展状况[J]. 锻造与冲压, 2005(4): 26.
[11] 王宏, 刘翠. 折弯机机架变形应力的有限元分析[J]. 重型机械, 2007(5): 56-58.
[12] 张开拓, 管殿柱, 白硕玮, 等. 基于响应面分析法的龙门式折弯机轻量化设计[J]. 制造业自动化, 2019, 41(1): 57-60.
[13] 范如明, 李恒, 吉桂生, 等. 模锻压力机机身结构与刚度分析[J]. 锻压装备与制造技术, 2016, 51(4): 19-22.
[14] 鞠家全, 邱自学, 崔德友, 等. 基于正交试验的机床移动横梁多目标优化设计[J]. 机械强度, 2018, 40(2), 356-362.
[15] 宋明顺, 黄佳, 张士朋, 等. 多指标正交试验设计去量纲准则及方法研究[J]. 工业工程与管理, 2014, 19(1): 41-46.
[16] 王巖, 隋思涟. 试验设计与MATLAB数据分析[M]. 北京: 清华大学出版社, 2012.
[17] 赵韩, 陈兴玉, 董玉德, 等. 参数化有限元分析的液压机机身轻量化设计[J]. 工程图学学报, 2010, 31(1): 20-25.
[18] 何晓群, 刘文卿. 应用回归分析[M]. 3版. 北京: 中国人民大学出版社, 2011.
[19] 陈宝林. 最优化理论与算法[M]. 2版. 北京: 清华大学出版社, 2005.
Lightweight Design of Gantry Bender Based on Orthogonal Test Method
LIN Guanyi, GUAN Dianzhu, ZHANG Kaituo, SONG Zhanjie
(School of Electromechanic Engineering, Qingdao University, Qingdao 266071, China)
Abstract: Aiming at the design of a gantry bending machine, computer simulation analysis is needed before it is put into production and work. The feasibility of the design scheme is verified and the lightweight design is carried out at the same time. Firstly, the threedimensional model of the bending machine is built by SolidWorks, which is imported into ANSYS Workbench 15.0. By applying load and pressure on the main parts of the bending machine and dividing the mesh, the analysis results of the overall deformation of the bending machine are obtained on the premise that the maximum stress of the material is less than the material yield limit value. According to the deformations of the bending machine, the structural optimization scheme is designed. Five parameters, namely, the thickness of the side plate of the table, the thickness of the supporting plate of the table, the thickness of the roof of the table, the diameter of the pull rod of the bending machine and the thickness of the stiffened plate of the upper pressure plate, are added. Orthogonal experiments are carried out, and the finite element analysis is done according to the test group numbers. The lightest weight of bending machine is the objective function. The boundary conditions of state variables and size variables are set. The lightweight model of bending machine is established. The model is solved by using Matlab software. The parameters are rounded and remodeled and analyzed by finite element method. Finally, the weight of the whole bending machine is reduced by 42 510 kg, and the working performance of the bending machine is guaranteed. The optimization effect is remarkable. This research has certain practical application value.
Key words: orthogonal test method; lightweight design; gantry bender; ANSYS Workbench; finite element analysis

