基于词频统计算法的中英文词频分布研究

李杰 孙仁诚

摘要：  针对幂律判断方式存在的问题，本文基于早期对幂律分布的研究，结合最大拟然拟合方法及词频统计算法，对中英文词频分布进行研究。給出了双对数坐标系下幂律分布的判断，并对词频统计与幂律分布进行拟合。研究结果表明，在双对数坐标系下，分布图像为近似直线是判断幂律分布的必要条件，而非充分条件;在自然语言的词频统计分布模型上，对观测数据进行幂律分布的拟合，得出的pvalue分别为0.14和0.19，均大于0.1，且泊松分布、指数分布、广延指数分布的pvalue值都为0，即可排除满足其他分布的假设，因此对观测数据拟合效果最好的是幂律分布。说明自然语言的词频分布满足幂律，且中英文同样适用。该研究对人们认识语言的发展过程具有重要意义。

关键词：  词频统计; 幂律分布; 最大似然估计; KS统计量

中图分类号： TP312; C81 文献标识码： A

收稿日期： 2019-06-20; 修回日期： 2019-10-28

基金项目：  国家自然科学青年基金资助项目（41706198）

作者简介：  李杰（1994-），男，硕士研究生，主要研究方向为数据挖掘与分析。

通信作者：  孙仁诚（1977-），男，副教授，博士，主要研究方向为数据挖掘及人工智能。Email： qdsunstar@163.com

幂律分布[1]广泛存在于计算机科学、人口统计学与社会科学、物理学、经济学与金融学等众多领域中，且形式多样。实验证明，在自然界与日常生活中，包括地震规模大小的分布、月球表面上月坑直径的分布、行星间碎片大小的分布、太阳耀斑强度的分布、计算机文件大小的分布、战争规模的分布、人类语言中单词频率的分布、大多数国家姓氏的分布、科学家撰写的论文数的分布、论文被引用的次数的分布、网页被点击次数的分布[2]、书籍及唱片的销售册数或张数的分布、电力数据的分布[3]、甚至电影所获得的奥斯卡奖项数的分布等都是典型的幂律分布。但这一结果存在巨大缺陷，曾经被认为满足幂律分布的某些数据，只有在一定的条件范围内才是幂律，而在整体大量的数据集上是不纯的[4]。20世纪中期，对于幂律分布的研究，一些研究者[5-6]分别在语言学和经济学的领域提出了著名的80/20定律。这一定律的基本形式即为简单的幂函数，是幂律分布的4种形式之一，其他形式的幂律分布有名次-规模分布、规模-概率分布等。直到21世纪初，A.L.Barabasi等人[7-8]提出了无标度理论，从复杂网络的角度探究了幂律分布的性质，即无标度网络的度分布就是幂律分布，为复杂网络的发展奠定了理论基础;C. Aaron等人[4]对幂律分布的判断标准进行了详尽的理论证明，推翻了前人通过双对数坐标系下是否构成一条近似直线判断幂律分布的方法，并证明了双对数坐标系下近似直线是幂律分布的必要条件。关于中英文词频分布的研究[9-11]一直是自然语言处理的重点。国内中文分词的算法主要集中在词典与统计相结合[12]的方式，但精度有待提升。2017年，麻省理工学院的Sun Junyi团队历时4年，完善了新的词频统计算法，与传统的基于统计的词频算法＼[13＼]不同，新的算法是基于前缀词典来实现词图扫描，构造有向无环图（directed acyclic graph，DAG），利用动态规划算法查找词频最大切合组，同时结合隐马尔可夫模型（hidden markov model，HMM）模型操作未登录词，大大提高了分词精度和分词效率。基于此，本文在最新词频统计算法基础上，构造私有的前缀词典及DAG，同时采用最新的幂律分布研究方式，对中英文两种语言进行研究，完善了之前研究者们[14-16]在词频统计精度及幂律分布判断方式上的不足之处，并进行了可视化的幂律拟合。该研究推动了人们对自然语言发展的认识。

1 幂律分布的研究

1.1 双对数坐标系下幂律分布的判断

20世纪末，人们对幂律分布的研究是基于双对数坐标系下，数据分布的图像是否为一条近似的直线来判断。幂律分布特征及其在双对数坐标系下的拟合如图1所示。

其形式化的表达为：y=cx-r，其中x，y表示正的随机变量;c，r为常数且均大于零。这种分布特征只有少数事件的规模比较大，而绝大多数事件的规模较小。对y-cx-r两边取对数，可知lny与lnx满足lny=lnc-rlnx，这是一种线性关系，即在双对数坐标系下，幂律分布可以通过一条斜率为负的幂指数的直线进行拟合，这一线性关系是判断给定的实例中随机变量是否满足幂律的依据。

判断两个随机变量是否满足线性关系，可以求解两者之间的相关系数;利用一元线性回归模型和最小二乘法，可得lny对lnx的线性回归方程，从而得到y与x之间的幂律关系式[1，4]。

对于在双对数坐标系下，线性关系判断数据是否满足幂律分布的说法不正确，因为双对数坐标系下的线性关系是数据满足幂律分布的必要条件，而不是充分条件。

1.2 幂律分布的判断

2007年，Aaron chauset等人[4]提出了判断幂律分布的一系列方法，其思想是将最大似然拟合方法与基于KolmogorovSmirnov（KS）统计以及似然比的拟合优度检验相结合，判断观测数据是否满足幂律分布，过程主要分为以下几部分：

1） 估计幂律模型的参数xmin和α。

2） 計算数据与幂律之间的拟合优度，如果得到的p-value值大于0.1，则幂律分布是观测数据的似然假设，否则拒绝该假设。

3） 通过似然比检验，将幂律与其他假设进行比较。对于每个备选方案，如果计算的似然比与零显著不同，则其符号表示该备选方案是否优于幂律模型。

2 词频统计与幂律分布拟合

关于自然语言中词汇的分布特征，早在20世纪中叶就有研究者进行过大量研究，直至20世纪末，有学者（幂律分布研究简史）通过双对数坐标系下图像近似一条直线的拟合方式，说明数据满足幂律分布，这种方式显然缺乏说服力。本文基于文献＼[4＼]提出的方法，首先基于词频统计算法对文本进行统计，然后结合最大似然拟合方法[17]与基于KolmogorovSmirnov（KS）统计[18]以及似然比[19]的拟合优度检验方式，对自然语言进行幂律分布的拟合。

关于数据的选择，本文选取了经典文学作品《飘》的中英文对照版本，分别对英文和中文进行词频统计，并拟合幂律分布。

2.1 词频统计算法

词频统计算法流程图如图2所示，词频统计算法整体分为3个部分，每个部分又可分为多个步骤，其描述如下：

1） 基于Trie树结构实现高效的词图扫描，构造出有向无环图（DAG），图中包括生成句子中汉字所有可能的成词情况。根据dict.txt生成trie树，字典在生成trie树的同时，也把每个词的出现次数转换为频率;对需要进行分词的句子，根据已经生成的trie树，生成有向无环图（DAG），简言之，就是将句子根据给定的词典进行查寻操作，生成多种可能的句子切分。

2） 用动态规划算法查找最大概率路径，找到基于词频的最大切分组合。查找待分词句子中已经切分好的词语，即查找该词语出现的频率，如果查不到该词，就把该词的频率赋值为词典中出现频率最小的那个词语的频率;根据动态规划算法查找最大概率路径，即对句子从后往前反向计算最大概率，P（NodeN）=1.0，P（NodeN-1）=P（NodeN）*Max（P（最后一个词））…依次类推，得到最大概率路径，从而得到最大概率的切分组合。

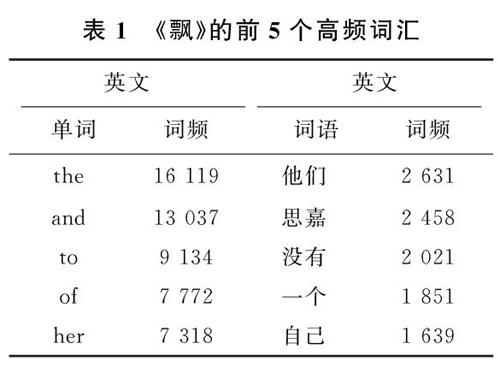
3） 对于词典中未录入的词，采用基于汉字成词能力的HMM模型，同时使用viterbi算法。中文词汇按照BEMS四个状态标记，B代表begin，即开始位置，E代表end，即结束位置，M代表middle，表示中间位置，S代表singgle，是单独成词的位置，如山东可表示为BE，即山/B，是开始位置，东/E，是结束位置;对语料库进行初步训练，得到3个概率表，并结合viterbi算法，可以得到一个概率最大的BEMS序列，按照B开始，E结尾的方式，对分词的句子重新组合，就能得到最终的分词结果[14]。对《飘》的中英文对照版词频进行统计，《飘》的前5个高频词汇如表1所示。

由表1可以看出，中英文在表达同义内容时，所使用词汇差别巨大，并未出现高频词汇一致性的现象，这与语言的特点有关。同时，英文的代词和介词在使用率上远高于其他词汇，而中文则不同，除代词外，量词在文章中也高频出现。虽然有诸多的差别，但在分布情况上仍需进一步验证。

2.2 幂律分布拟合

本文通过将最大似然拟合方法与基于KolmogorovSmirnov（KS）统计以及似然比的拟合优度检验相结合的方式，对自然语言进行了幂律分布拟合。中英文词频在双对数坐标系下的幂律拟合如图3所示。图3中，英文词频xmin=40，α=1.89;中文词频xmin=38，α=2.1。

由图3可以看出，在双对数坐标系下，中英文的词频分布均呈现一条近似的直线，说明存在幂律分布的可能性，但需要验证pvalue是否大于0.1，如果大于0.1，就要进一步排除其他分布是否比幂律分布拟合效果更好，否则，可以直接判断不满足幂律分布。似然比的拟合优度LR值和pvalue（p）值如表2所示。

由表2可以看出，对观测数据进行幂律分布的拟合，得出的pvalue分别为0.14和0.19，均大于0.1，且泊松分布，指数分布，广延指数分布的pvalue值都为0，即满足其他分布的假设可直接排除，因此对观测数据拟合效果最好的是幂律分布。

3 结束语

本文通过对中英文词频的统计分析，证明了自然语言中的词汇在日常生活中的使用频率是服从幂律分布的，即部分词汇会被大量使用，大部分词汇的使用频率较低，符合动力学中的省力原则，人们更倾向于用更少词汇的不同组合来表达不同的意思，对认识语言的发展过程具有重要意义。这一结论不仅仅出现在本文所研究的文献中，对于其他文献同样适用。文中词频统计算法和“最大似然拟合方法”、“KS统计以及似然比的拟合优度检验方法”的结合，使本结论的精确度更高，进一步补充了前人对于词频分布的研究与应用。在接下来的工作中，可以将重点放在对其他语言的研究上，在幂律分布的基础之上，探究是否有更加精确的拟合方式，进一步推动人们对于自然语言发展的认识。

参考文献：

[1] 胡海波， 王林. 幂律分布研究简史[J]. 物理， 2005， 34（12）： 889-896.

[2] Adamic L A， Huberman B A， Barabási A L， et al. Powerlaw distribution of the world wide web[J]. Science， 2000， 287 （5461）： 2115a.

[3] 王冠男， 邓春宇， 赵悦， 等. 电力数据中的幂律分布特性[J]. 电信科学， 2013， 29（11）： 109-114， 121.

[4] Aaron C， Cosma R S， Newman M E J. Powerlaw distributions in empirical data[J]. Siam Review， 2009， 0706（1062）： 661-703.

[5] 严怡民. 情报学概论[M]. 武汉： 武汉大学出版社， 1994.

[6] Arnold B C. Pareto Distribution[M]∥Encyclopedia of Statistical Sciences. United States： John Wiley & Sons， Inc.， 2006.

[7] Barabasi A L， Albert R. Emergence of scaling in random networks[J]. Science， 1999， 286（5439）： 509-514.

[8] Barabasi A L， Bonabeau E. Scalefree networks[J]. Scientific American， 2003， 288（5）： 60.

[9] 张丹. 中文分词算法综述[J]. 黑龙江科技信息， 2012（8）： 206.

[10] 张华平， 刘群. 基于N-最短路径方法的中文词语粗分模型[J]. 中文信息学报， 2002， 16（5）： 1-7.

[11] 费洪晓， 康松林， 朱小娟， 等. 基于词频统计的中文分词的研究[J]. 计算机工程与应用， 2005， 41（7）： 67-68， 100.

[12] 秦赞. 中文分詞算法的研究与实现[D]. 长春： 吉林大学， 2016.

[13] 祝永志， 荆静. 基于Python语言的中文分词技术的研究[J]. 通信技术， 2019， 52（7）： 1612-1619.

[14] Goldstein M L， Morris S A， Yen G G. Fitting to the powerlaw distribution[J]. The European Physical Journal BCondensed Matter and Complex Systems， 2004， 41（2）： 2004.

[15] Fernholz R T. Nonparametric methods and locatimebased estimation for dynamic power law distributions[J]. Journal of Applied Econometrics， 2016， 32（7）： 1244-1260.

[16] Montebruno P， Bennett R J， van Lieshout C， et al. A tale of two tails： Do power law and lognormal models fit firmsize distributions in the midvictorian era[J]. Physica A： Statistical Mechanics and its Applications， 2019， 523： 858-875.

[17] 胡德， 郭剛正. 最小二乘法、矩法和最大似然法的应用比较[J]. 统计与决策， 2015（9）： 20-24.

[18] Lilliefors H W. On the kolmogorovsmirnov test for normality with mean and variance unknown[J]. Journal of the American Statistical Association， 1967， 62（318）： 399-402.

[19] 成平. 极大似然估计与似然比检验的几点注记[J]. 应用概率统计， 2003， 19（1）： 55-59.

Research on Chinese and English Word Frequency Distribution Based on Word Frequency Statistics Algorithm

LI Jie， SUN Rencheng

（College of Computer Science & Technology， Qingdao University， Qingdao 266071， China）

Abstract：  Aiming at the problems existing in the power law judgment method， this paper studies the frequency distribution of Chinese and English words based on the previous research on power law distribution， combined with the maximum likelihood fitting method and word frequency statistics algorithm. The judgment of power law distribution in double logarithmic coordinate system is given， and the word frequency statistics and power law distribution are fitted. The results show that in the double logarithmic coordinate system， the distribution image being an approximate straight line is a necessary condition for judging the power law distribution， but not a sufficient condition. On the word frequency statistical distribution model of natural language， the power law distribution of the observation data is proposed. The pvalues obtained are 0.14 and 0.19， respectively， both greater than 0.1， and the pvalues of the Poisson distribution， the exponential distribution， and the extensive exponential distribution are all 0， that is， the assumptions satisfying other distributions can be directly excluded. The best fit for the observation data is the power law distribution. It shows that the word frequency distribution of natural language satisfies the power law， and both Chinese and English are applicable. This research is of great significance for people to understand the development process of language.

Key words：  word frequency statistics; power law distribution; maximum likelihood estimation; KS statistics