后驱式纯电动车再生制动控制策略研究
孟泽文 张铁柱 张洪信 赵清海 尹怀仙 侯典平
摘要: 针对电动汽车再生制动力中制动力分配系数不合理的问题,本文以后驱式纯电动汽车为研究对象,通过分析制动力安全分配区域,在isight软件中对制动力分配区域优化,得出最优分配区间,并在此基础上提出新型再生制动控制策略。同时,在AVL_cruise中建立电动汽车整车模型,在Matlab/Simulink中建立再生制动控制策略模型,并在不同制动强度工况下进行联合仿真。仿真结果表明,与原控制策略相比,新控制策略在中制动强度制动时的能量回收率明显提高,在高、大制动强度时电动汽车的制动稳定性提升,说明该控制策略是合理的。该研究为电动汽车对再生制动深入研究能量回收率以及制动稳定性等方面提供了理论基础。
关键词: 后驱电动汽车; 再生制动; 控制策略; 优化; 仿真
中图分类号: U469.72 文献标识码: A
收稿日期: 2019-08-16; 修回日期: 2019-10-28
基金項目: 山东省自主创新及成果转化专项(40215020073);山东省科技发展计划项目(2014GGX103044);青岛市战略性新兴产业培育计划项目(14-8-1-2-gx)
作者简介: 孟泽文(1996-),男,山东泰安人,硕士研究生,主要研究方向为电动汽车智能化动力集成技术。
通信作者: 张洪信(1969-),男,山东潍坊人,博士,教授,主要研究方向为电动汽车智能化动力集成技术。Email: qduzhx@126.com
随着汽车工业的迅速发展,随之带来了严重的环境污染和石油资源枯竭问题[1]。近年来,电汽车发展迅速和应用广泛,但其续驶里程短、动力性不足的问题仍然没有得到解决。再生制动能够回收一部分制动时产生的能量,提高能量的利用率,增加汽车的续驶里程,因此再生制动控制策略对电动汽车的研究具有重要意义[2-4]。付先成等人[5]基于XQ6103客车对再生制动系统进行分析,最终确定整车制动力分配系数在0.4~0.5之间取值比较合理;邓姣艳[6]以纯电动公交车位为依据,选取磷酸铁锂电池和超级电容组成的复合电源,采用Simulink进行仿真实验,实验结果证明储能效果比单一电源提高了15%;M. Panagiotidis等人[7]经过仿真研究发现,在不降低驾驶员感受的前提下,在多个典型工况下,串联式制动能量回收系统性能比并联式能量回收好,回收率达到20%以上;Hoon Y等人[8]提出了四轮混合驱动混合动力的制动力分配控制策略,并结合模糊控制,进一步提出再生控制系统和四轮液压和ABS控制的方法,实现再生制动的总体控制。目前,再生制动主要存在制动稳定性和制动能量回收不能兼顾的问题[9-11]。基于此,本文以制动力分配的角度为出发点,以后驱式纯电动汽车为例,对制动力分配安全区域进行优化,提出了新型再生制动控制策略,在保证汽车稳定性的基础上回收能量最大化。通过联合仿真,验证了该控制策略的有效性和可行性。该研究为电动汽车再生制动控制策略的深入研究提供了理论依据。
1 制动能量回收原理
传统燃油汽车主要靠制动盘与车轮的摩擦实现汽车的制动减速,制动时汽车的动能转换为热能损耗[12]。与传统燃油汽车相比,电动汽车在制动过程中,车轮通过传动系统带动电动机发电,将能量储存在电池中,同时,电动机发电过程中产生的反拖转矩通过传动系统传递到车轮,实现汽车的制动[13]。
汽车在制动过程中,纵向平面受滚动阻力Ff、空气阻力Fw、坡度阻力Fi和地面制动力Fb的共同作用。汽车制动动力学方程为
Ft=Ff+Fb+Fi+Fw(1)
式中,Ft为总需求制动力。
假设制动前车速为V1,制动过程结束后的车速为V2,则在整个制动过程中动能的损失为
(mV12)/2—(mV22)/2=FtS(2)
式中,S为制动距离。
在城市交通工况下,可以忽略坡度阻力Fi和空气阻力Fw[14],所以式(2)可以简化为
(mV12)/2—(mV22)/2=(Ff+Fb)S(3)
式中,m为汽车质量;Ff为滚动阻力;Fb为地面制动力。滚动阻力以热能的形式散发,无法回收。汽车制动力包括再生制动力和传统机械制动力,机械制动力产生的能量最终转换为热能,是无法回收的,只有电机再生制动力消耗的一部分能量转换为转矩才可以回收[15],所以如何分配制动力的比例和工作模式是影响能量回收利用率的重要因素。
2 制动力分配控制策略
2.1 制动力分配范围
对于传统汽车,根据前后轮制动力的分配情况、路面附着系数等因素,汽车制动时会出现以下3种情况[16]:
1) 前轮先于后轮抱死。这种情况发生时,前轮因抱死而失去转向能力,没有充分的利用附着条件。
2) 后轮先于前轮抱死。汽车容易发生侧滑等危险工况,比前轮先抱死更危险。
3) 前后车轮同时抱死。相比于前两种情况,此时前后附着系数相等,充分利用附着系数。
因此,制动力分配是否合理对汽车制动过程中的稳定性影响很大,理想的前、后制动力分配为I曲线,该曲线制动力满足
Fr=12Ghgb2+4hglGFf-(Gbhg+2Ff)(4)
式中,Ff和Fr分别为前、后轮地面制动力;b为质心与后轴的距离;hg为质心高度;G为作用在整车上的重力;l为轴距。
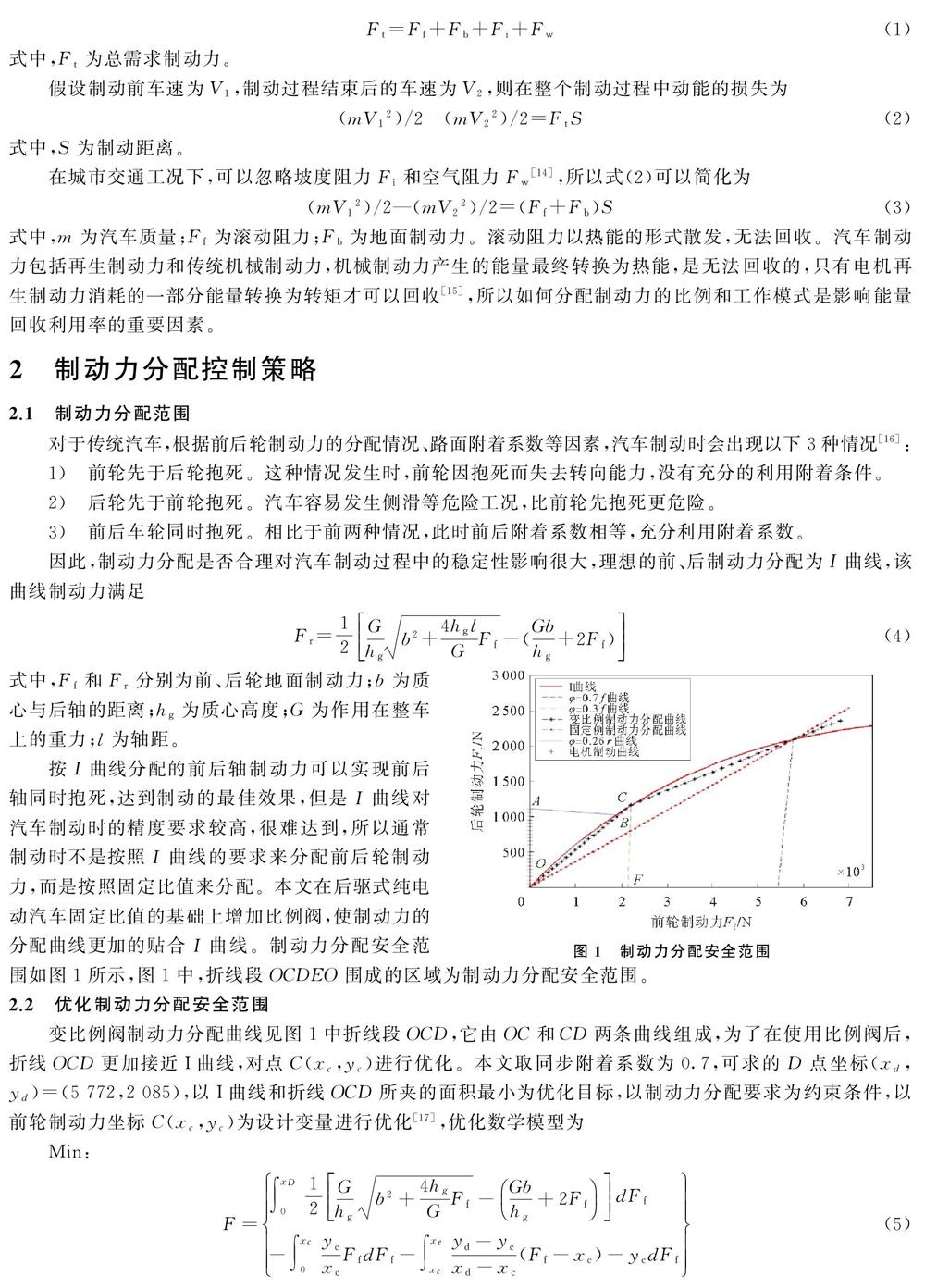
按I曲线分配的前后轴制动力可以实现前后轴同时抱死,达到制动的最佳效果,但是I曲线对汽车制动时的精度要求较高,很难达到,所以通常制动时不是按照I曲线的要求来分配前后轮制动力,而是按照固定比值来分配。本文在后驱式纯电动汽车固定比值的基础上增加比例阀,使制动力的分配曲线更加的贴合I曲线。制动力分配安全范围如图1所示,图1中,折线段OCDEO围成的区域为制动力分配安全范围。
2.2 优化制动力分配安全范围
变比例阀制动力分配曲线见图1中折线段OCD,它由OC和CD两条曲线组成,为了在使用比例阀后,折线OCD更加接近I曲线,对点C(xc,yc)进行优化。本文取同步附着系数为0.7,可求的D点坐标(xd,yd)=(5 772,2 085),以I曲线和折线OCD所夹的面积最小为优化目标,以制动力分配要求为约束条件,以前轮制动力坐标C(xc,yc)为设计变量进行优化[17],优化数学模型为
Min:
F=∫xD012Ghgb2+4hgGFf-Gbhg+2FfdFf-∫xc0ycxcFfdFf-∫xexcyd-ycxd-xc(Ff-xc)-ycdFf(5)
S.t.: yc=Ghgb2+4hgGxc-Gbhg+2xc(6)
0≤xc≤57 720(7)
设计变量优化如图2所示。
通过优化软件isight优化,在迭代1 002次之后得到优化后的C点坐标(xc,yc)为(2 305,1 154),即得到直线OC和CD的方程分别为
Fr=0.5Ff(8)
Fr=0.252 1Ff+573(9)
2.3 前后轮制动力分配
1) 当制动强度0
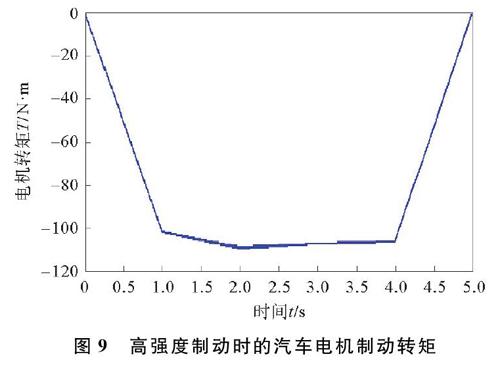
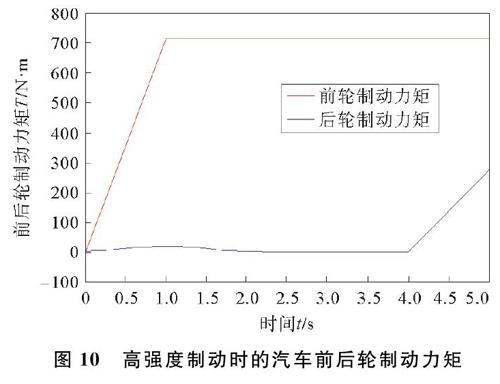
2) 当制动强度0.1 Freg=-0.047 6Ff+1 111.6(10) 式中,Freg为电机制动力。 3) 当制动强度0.26 Freg=Freg_max(11) F′r=Fr-Freg(12) Fr=0.5Ff(13) 式中,Freg_max为最大的再生制动力;F′r为后轮机械制动力。CD线段的制动力分配方法和BC线段相同,此时 Freg=Freg_max(14) F′r=Fr-Freg(15) Fr=0.252 1Ff+573(16) 4) 当制动强度z>0.7时,为大强度制动,属于紧急制动状态,为了保证制动安全性,制动过程中电机退出再生制动,只有机械制动。此时 Freg=0(17) Fr=F′r=0.252 1Ff+573(18) 3 再生制动系统建模 使用Matlab/Simulink软件搭建车辆再生制动控制模型,汽车制动过程中,电机制动力和机械制动力分配控制策略如图3所示。 使用AVL_cruise搭建整车模型,本文所采用的目标车型为后驱式纯电动汽车,电机输出轴通过主减速器与后轮相连,电动汽车主要参数如表1所示。 利用AVL_cruiseInterface模块做为接口,将整车模型中的车速、制动压力、转速等信号变量输入到Matlab/Simulink中,同时输出电机负荷信号、电机制动力、前轮制动力以及后轮制动力等信号[20],对车辆进行控制,其实际作用相当于实车中的制动控制单元(brake control unit,BCU)。用AVL_cruise搭建车辆模型,cruise整车模型如图4所示。 4 仿真结果分析 以初始车速为100 km/h和80 km/h,并选取几种不同的制动强度,对本文提出的再生制动控制策略进行实验验证。小强度制动时的汽车电机制动转矩如图5所示,小强度制动时的汽车前后轮制动力矩如图6所示。 6 小强度制动时的汽车前后轮制动力矩 由图5和图6可以看出,当汽车在小强度制动工况下,只有电机产生制动力矩,前轮和后轮不产生机械制动,说明电机制动足以满足汽车制动需求。当车速降低到10 km/h时,电机退出再生制动,此时前后轮的机械制动力矩增大,汽车完全由机械制动完成汽车制动。 中强度制动时的汽车电机制动转矩如图7所示,中强度制动时的汽车前后轮制动力矩如图8所示。 由图7和图8可以看出,当汽车进行中强度制动时,制动时间为18 s左右,电机的输出转矩一直发生变化,当电机制动力不足时,前轮开始机械制动,对电机制动力进行补偿,电机的最大输出转矩在78 N·m左右并保持稳定,前后轮的制动力矩保持不变。当车速减小到10 km/h时,电机制动力退出再生制动,前后轮的机械制动增大保证制动力矩的稳定性。 高强度制动时的汽车电机制动转矩如图9所示,高强度制动时的汽车前后轮制动力矩如图10所示。 由图9和图10可以看出,当汽车进行中强度制动时,制动时间为5 s左右,电机的输出的转矩沿其外特性曲线变化,当电机制动力不足时,前轮开始机械制动,对电机制动力进行补偿。 电机的最大输出转矩在110 N·m左右并保持稳定,前后轮的制动力矩保持不变。当车速减小到10 km/h时,电机制动力退出再生制动,前后轮的机械制动增大保证制动力矩的稳定性。 当汽车处于高强度制动时,电机不参与汽车制动,故提供的制动转矩为0,汽车所需的制动力矩全部由前后轮的机械制动力矩来提供。选择制动能量回收率作为评价能量回收效果的指标,即 ηreg=WchgW=Wchg12mV13.62-V23.62(19) 式中,ηreg为电池的能量回收率;Wchg为进入到蓄电池的充电能量;W为汽车制动时消耗的能量;V1为制动前的车速;V2为制动后的车速。 根据式(19),在3种不同工况下,计算电动汽车的制动能量回收率,制动能量回收率如表2所示。 5 结束语 本文主要对后驱式纯电动汽车的再生制动控制策略进行研究,提出了一种基于制动强度解耦式串联再生制动控制策略,并搭建了控制策略模型和整车模型,并对该控制策略进行仿真验证,仿真结果表明,当电动汽车在中小强度制动时,可以充分利用电机的再生制动,回收效率较高。在高制动强度下制动时,为了保证汽车的制动安全性,电机再生制动明显减少,能量回收率下降。在大制动强度下,电机完全退出再生制动,以保证汽车制动稳定性。本文的再生制动控制策略方面并没有考虑到电池的充放电特性对制动力分配的影响以及制动过程的平顺性。后续应进一步深入对再生制动控制策略的研究,以提高电动汽车的能量回收率以及制动平顺性。 参考文献: [1] 郭栋, 朱文平, 孙宇航, 等. 城市电动公交车制动能量回收控制策略研究[J]. 汽车工程, 2016, 38(3): 269-273. [2] 郭陈栋. 电动车辆再生制动系统控制策略的研究[D]. 合肥: 安徽农业大学, 2013. [3] 李欣, 王佳. 節能汽车制动能量回收与再利用[J]. 机械设计与制造, 2016(4): 91-93, 97. [4] 刘红亮, 董学平, 张炳力. 电动汽车再生制动控制策略的研究[J]. 合肥工业大学学报: 自然科学版, 2012, 35(11): 1484-1487. [5] 付先成, 张保成, 颜波. 电储能车辆再生制动系统制动力分配系数设计[J]. 机械工程与自动化, 2014(2): 123-125. [6] 邓姣艳. 电动公交再生制动储能系统研究[D]. 成都: 西南交通大学, 2014. [7] Panagiotidis M, Delagramraatikas G, Assanis D. Development and use of a regenerative braking model for a parallel hybrid electric vehicle[C]∥SAE 2000 World Congress State of Michiga. USA: SAE, 2000. [8] Hoon Y, Hyunsoo K. Development of regenerative braking hydraulic module and HIL simulator for hybrid electric vehicle[C]∥Proceeding of the 23rd Chinese Control Conference. Shanghai: East China University of Science of Technology Press, 2004: 1551-1556. [9] 金宇華, 张庭芳, 刘建春. 混合动力电动汽车制动力分配及能量回收控制策略研究[J]. 机械传动, 2011, 35(12): 34-36, 52. [10] 余志生. 汽车理论[M]. 北京: 机械工业出版社, 2009. [11] 赖锋. 重型汽车制动系统结构分析及其设计方法研究[D]. 武汉: 武汉理工大学, 2006. [12] 王耀南, 刘东奇. 电动汽车机电复合制动力分配策略研究[J]. 控制工程, 2014, 21(3): 347-351, 356. [13] 刘鹏. 基于iSIGHT平台的多学科多目标优化设计[D]. 西安: 西安理工大学, 2012. [14] 张京明, 王仕伟, 程志刚, 等. 混合动力汽车再生制动系统的建模与仿真[J]. 计算机仿真, 2008, 25(7): 268-272. [15] 刘果. 后驱型纯电动汽车再生制动系统的研究[D]. 太原: 太原理工大学, 2016. [16] 周英超, 李训明, 曲金玉. 后驱并联式液压再生制动汽车制动力分配研究[J]. 农业装备与车辆工程, 2013, 51(2): 9-13. [17] 初亮, 蔡健伟, 富子丞, 等. 纯电动汽车制动能量回收评价与试验方法研究[J]. 华中科技大学学报: 自然科学版, 2014, 42(1): 18-22. [18] 陈斌. 纯电动汽车再生制动研究[D]. 重庆: 重庆大学, 2011. [19] 张亚军, 杨盼盼. 纯电动汽车再生制动系统的建模与仿真[J]. 武汉理工大学学报, 2010, 32(15): 90-94. [20] 杨亚娟, 赵韩, 李维汉, 等. 电动汽车再生制动与液压ABS系统集成控制研究[J]. 合肥工业大学学报: 自然科学版, 2012, 35(8): 1054-1058, 1125. Brake Energy Recovery Control Strategy for Rear Drive Pure Electric Vehicle MENG Zewena, ZHANG Tiezhua,b, ZHANG Hongxina,b, ZHAO Qinghaia,b, YIN Huaixiana,b, HOU Dianpinga (a. School of Electromechanic Engineering, Qingdao University, Qingdao 266071, China;b. Power Integration and Energy Storage Systems Engineering Technology Center, Qingdao University, Qingdao 266071, China) Abstract: In view of unreasonable power distribution coefficient of electric vehicles, this paper mainly stu dies of rear drive pure electric vehicle. By analyzing the safety distribution area of braking force, with the iSIGHT software, the braking force distribution area is optimized, and the optimal distribute on interval is obtained. On this basis, a new regenerative braking control strategy is put forward. The whole vehicle model of electric vehicle is established in AVL_cruise, and the regenerative br aking control strategy model is established in matlab/Simulink. Joint simulation is carried out under different braking intensity conditions. Simulation results show that, compared with the original control strategy, The energy recovery rate of the new control strategy is obviously improved when the middle braking intensity is applied, and the braking stability of electric vehicle is improved at high and big braking intensity. It shows that the control strategy is reasonable, and provides a theoretical basis for the regenerative braking of electric vehicles, indepth study of energy recovery and braking stability. Key words: rear drive electric vehicle; braking energy recovery; control strategy; optimize; simulation

