基于自适应控制的空气舵位置伺服系统研究

(北京精密机电控制设备研究所, 北京 100076)

本研究以某飞行器空气舵位置伺服系统为研究对象，基于Popov超稳定性原理，设计模型参考自适应控制器，降低模型参数不确定性对系统控制性能的影响，提高空气舵位置伺服系统的定位精度和鲁棒性。

引言

空气舵位置伺服系统是导弹制导与控制系统的执行机构，通过带动舵面摆动实现弹体的姿态控制[1-2]。空气舵位置伺服系统按照能源分类，主要可分为液压伺服系统、气动伺服系统、机电伺服系统三大类。空气舵位置机电伺服系统是一个高阶、多变量、强耦合非线性系统，存在诸多不利于控制性能提高的因素，如摩擦力矩、电机力矩波动、驱动饱和、耦合力矩等，其数学模型非常复杂。因此，将经典控制理论和现代控制理论相结合，应用于高精度、快响应的位置伺服系统中，成为伺服领域研究人员的重要研究课题[3]。

针对位置伺服系统高精度非线性控制问题，国内外学者对其进行了研究，主要控制策略有：自抗扰控制[4]、模糊PID控制[5]、滑模控制[6]、自适应控制[7-10]等。其中，模型参考自适应控制(Model Reference Adaptive Control，MRAC)作为一种先进的控制策略，其应用由机械臂运动控制、船舶自动驾驶、飞行器控制等逐步扩展到电机的运动控制领域[8]。

1 空气舵位置伺服系统建模

空气舵位置伺服系统建模的关键是建立准确的永磁电机模型和负载对象模型。永磁电机是典型的多变量高阶非线性系统，其本质模型是高阶微分方程组。根据电机相关理论，永磁电机的特性方程经坐标变换之后可以用转子同步坐标系d-q轴系方程来表示。

(1) 电机电压平衡方程：

(1)

式中，ud，uq—— 定子电压在d轴和q轴上的分量

id，iq—— 定子电流在d轴和q轴上的分量

ψd,ψq—— 定子磁链在d轴和q轴上的分量

ωr—— 电机转子同步旋转坐标系角速度

(2) 电机磁链方程：

(2)

式中，Ld,Lq——d，q轴线圈的自感

ψf—— 转子永磁体磁极的励磁磁链

(3) 电机电磁转矩方程:

(3)

式中，Te—— 电机输出转矩

pm—— 电机极对数

(4) 电机转子机械运动方程：

(4)

式中，J—— 转子当量转动惯量

ωm—— 电机转速

B—— 电机转子摩擦系数

TL—— 负载转矩

(5) 空气舵负载运动方程:

(5)

式中，Jp,Bp—— 空气舵转动惯量和黏性阻尼系数

δ—— 空气舵摆角

Tf—— 舵轴摩擦力矩

本型空气舵位置伺服系统采用id=0控制策略，其q轴通道系统传递框图如图1所示。

空气舵位置伺服系统主要仿真参数如表1。

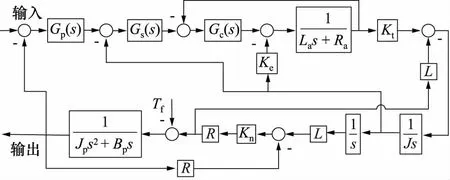
图1 空气舵位置伺服系统传递框图

表1 伺服系统主要参数值

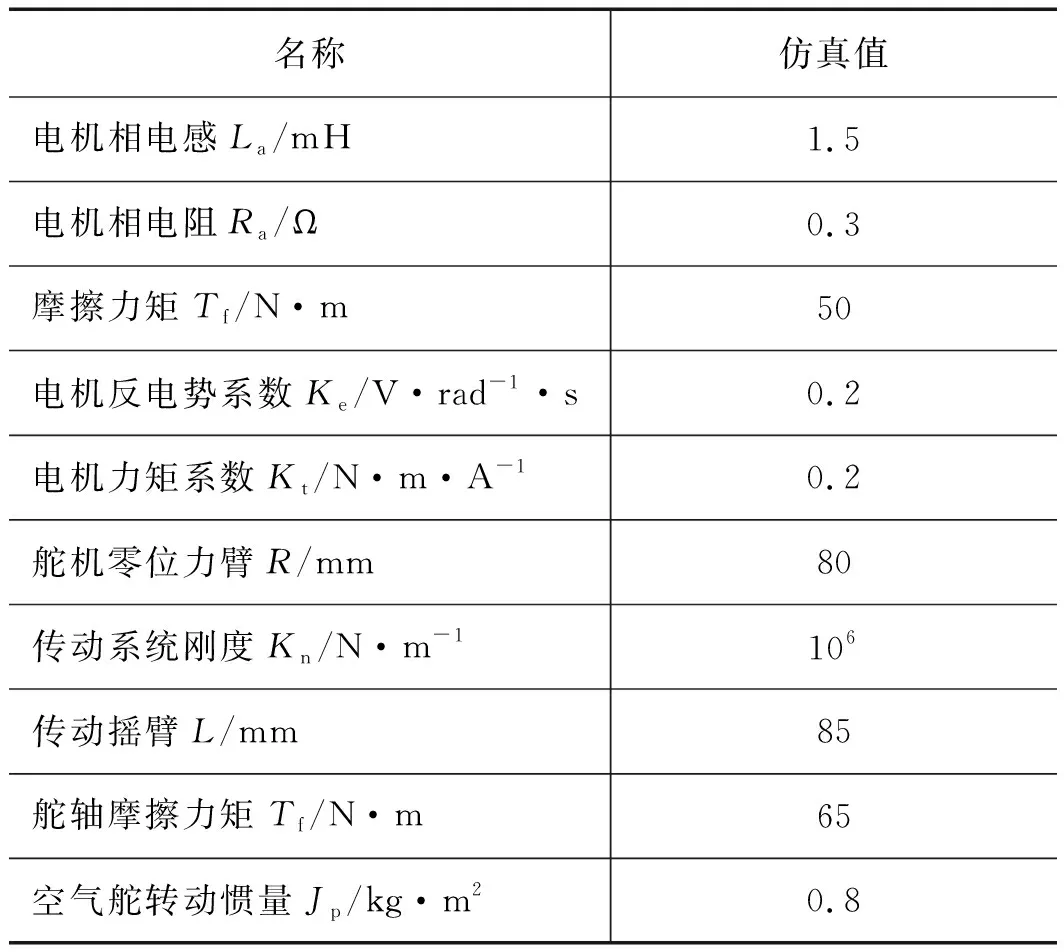
名称仿真值电机相电感La/mH1.5电机相电阻Ra/Ω0.3摩擦力矩Tf/N·m50电机反电势系数Ke/V·rad-1·s0.2电机力矩系数Kt/N·m·A-10.2舵机零位力臂R/mm80传动系统刚度Kn/N·m-1106传动摇臂L/mm85舵轴摩擦力矩Tf/N·m65空气舵转动惯量Jp/kg·m20.8

忽略空气舵轴黏性阻尼影响，通过MATLAB/Simulink线性化分析工具箱可求出系统的闭环传递函数为：

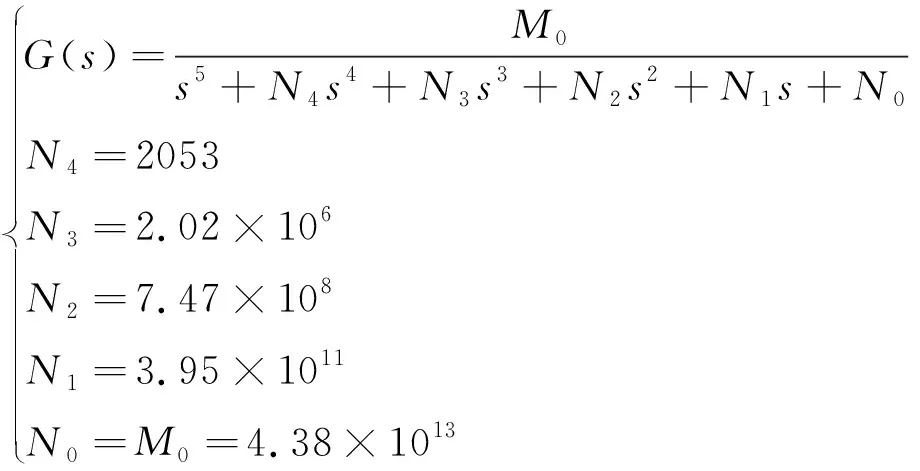
(6)

空气舵位置伺服系统是一个五阶系统，传递函数分母的五次项和四次项系数较小。图2是五阶传递函数及三阶近似函数的伯德图，可见，在空气舵伺服系统工作频段0到340 rad/s范围内，系统传递函数模型可简化为三阶系统。

2 模型参考自适应控制系统设计

模型参考自适应控制系统的核心是设计稳定高性能的自适应算法，其本质是使负载对象与参考模型的输出特性保持一致。

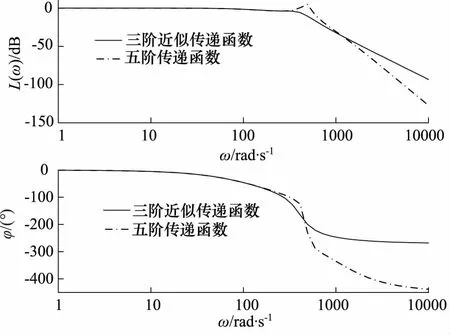
图2 空气舵伺服系统传递函数Bode图

2.1 基于MRAC的空气舵位置伺服系统

图3是采用MRAC的空气舵位置伺服系统的结构图。对于空气舵位置伺服系统而言，位移可通过线位移传感器直接测得，速度可通过旋转变压器间接测得，加速度可以通过数学计算间接获取。

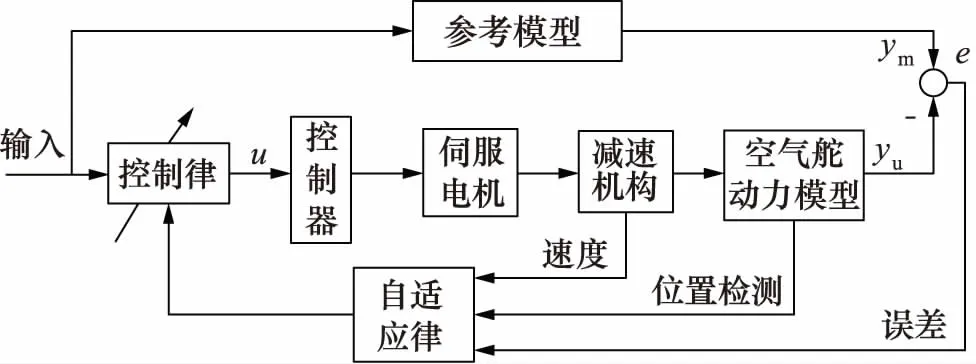
图3 空气舵MARC位置伺服系统

基于Popov超稳定性理论设计模型参考自适应控制系统的步骤如下[11]：

(1) 通过非线性孤立法，将MRAC系统规范为线性环节和非线性环节构成的等价反馈系统；

(2) 采用Popov积分不等式处理非线性环节，得出反馈通道的自适应律部分解；

(3) 采用正实定理处理线性环节，确定正向通道控制律的部分解；

(4) 设计结果校验，若满足要求，则将前三步计算结果表示为显式模型参考自适应系统，否则返回步骤(1)，直到性能符合要求。

2.2 机电伺服系统自适应控制律

1) 空气舵位置伺服系统模型

空气舵位置伺服系统采用三阶系统近似表示，其状态空间方程为：

(7)

系统的输出方程为：

y=[1 0 0][x1x2x3]′

(8)

2) 参考模型及状态方程

结合空气舵位置伺服系统的性能特点，参考模型的设计原则如下：

(1) 参考模型与对象模型阶数均为三阶；

(2) 参考模型的动态特性符合空气舵面位置伺服系统性能要求；

(3) 位置超调容易导致空气舵传动机构受损，因此，超调量指标着重考虑。

选择参考模型状态方程为：

(9)

参考模型的输出方程为：

y=[1 0 0][x4x5x6]′

(10)

3) 自适应控制律的确定

引入补偿器D(s)：

D(s)=d2s2+d1s+d0

(11)

D(s)/Am(s)严格正实，则D(s)应满足：

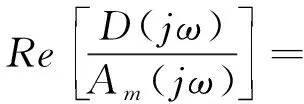
(12)

自适应控制器广义输出误差为：

ed(t)=D(s)(yu-ym)=d2(x3-x6)+

d1(x2-x5)+d0(x1-x4)

(13)

状态滤波器的输出信号为ξ1，ξ2，ξ3，ξ4，自适应控制器参数调节律为：

(14)

系统的控制输入为：

(15)

空气舵位置伺服系统设计自适应控制系统框图如图4所示。

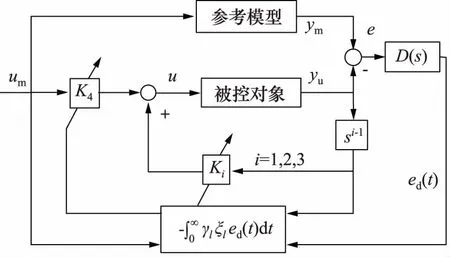
图4 空气舵位置伺服系统MRAC控制方框图

3 仿真结果及分析

取参考模型为：

(16)

补偿器D(s)=s2+200s+8000,γi=10000，在Simulink中搭建系统仿真模型如图5所示[12]。

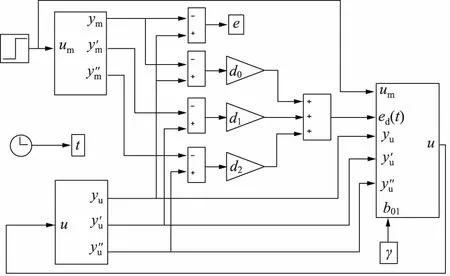
图5 空气舵位置伺服系统MRAC仿真模型

系统建模过程对传递环节进行了线性化处理，但系统物理参数因工况差异、温度差异和机械尺寸散差等因素而动态变化。在仿真模型中，分别设置50%～200%范围电机力矩系数名义值，对比分析空气舵摆角的跟踪性能，结果如图6、图7所示。可见，当电机力矩系数变化时，PID控制条件下空气舵摆角响应超调量较大，且输出摆角值受电机力矩系数变化而明显波动；MRAC下的空气舵摆角单位阶跃输入信号下输出无超调，且输出摆角值受电机力矩系数变化的影响较小，具有良好鲁棒性能。

空气舵位置伺服系统工作过程中，主要克服空气舵面铰链力矩做功，铰链力矩与大气密度、空气舵面积和飞行速度等密切相关，是典型的非线性强时变负载。在仿真模型中施加幅值300 N·m、持续时间30 ms的周期脉冲信号，模拟飞行过程中干扰铰链力矩情况，伺服系统的阶跃响应如图8所示。结果表明PID控制条件下空气舵摆角波动明显，摆角输出偏差约16%；MRAC下的空气舵摆角略有变化，摆角输出偏差约3%，表现出对外负载干扰的良好鲁棒性能。

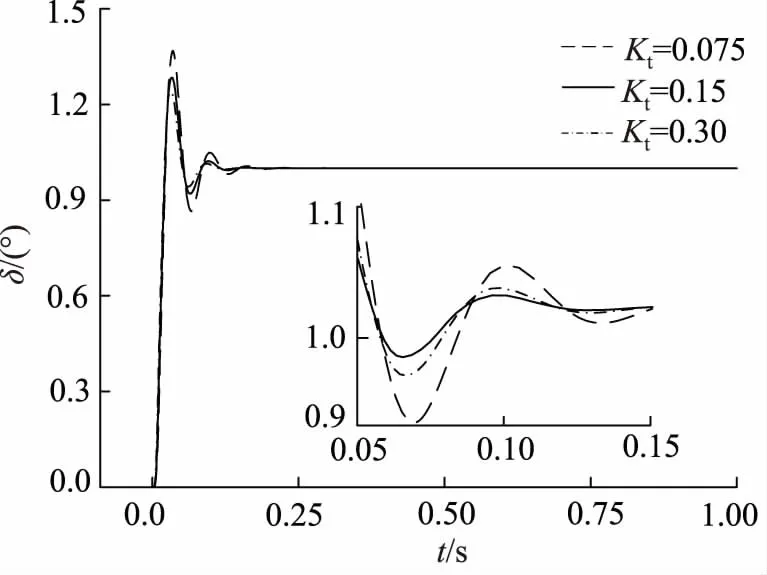
图6 电机力矩系数变化下PID控制响应曲线

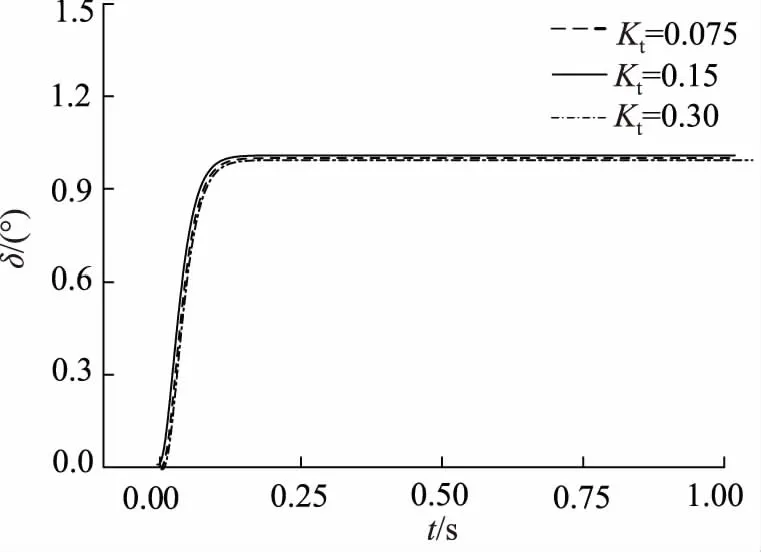
图7 电机力矩系数变化下MRAC控制响应曲线

4 结论

通过研究自适应控制策略在空气舵位置伺服系统上的应用，建立和简化了伺服系统的数学模型，提出了系统的模型参考自适应控制律设计方案，并在Simulink中完成建模和仿真，通过以上设计与仿真分析。

可得如下结论:

(1) 本研究空气舵位置伺服系统是一个五阶系统，结合系统的实际工况，系统可简化为三阶系统，从而简化模型参考自适应控制律的设计方案；

(2) 在伺服系统的状态空间模型基础上，利用Popov超稳定性理论，通过引入补偿器，可以快速迭代设计系统的自适应控制器；

(3) 空气舵位置自适应控制系统相比常规PID控制系统具备更好的定位精度，同时，自适应控制系统对自身参数不确定性和外负载干扰表现出良好鲁棒性能。