基于Bell态纠缠交换的量子盲签名方案

郑 涛 张仕斌 昌 燕 李雪杨

(成都信息工程大学 四川 成都 610225)

0 引 言

1984年Bennett和Brassard提出了第一个量子密码协议，即BB84协议[1]。随后科研工作者们提出了大量的量子密码协议与量子通信协议，包括量子密钥分发协议(QKD)[2-4]、量子直接安全通信协议(QSDC)[5-7]、量子秘密共享协议(QSS)[8-9]、量子隐私查询协议(QPQ)[10-15]等。

电子签名的概念由Diffie和Hellman在1976年第一次提出[11]，1983年Chaum等基于电子签名提出了盲签名的概念。盲签名协议的基本要求有：(1)不可伪造性，除签名人之外没有人可以伪造签名。(2)不可否认性，消息拥有者和签名人都不能否认自己对消息的操作。(3)盲性，签名者不能将自己的签名与消息对应起来。盲签名方案在现实生活中有着广泛的应用，比如匿名选举、电子现金交易等。

随着量子技术的不断发展，量子计算机的出现将会使基于数学计算复杂性的签名方案变得不再安全。研究人员在过去的十多年内开始研究基于量子信息的签名协议。2001年Gottsman等[16]提出了基于量子单向函数的签名方案。曾贵华等[17]于同年提出了基于GHZ态的量子仲裁签名方案。这两个方案都要求一个可信的第三方来完成认证。2009年温晓军等[18]提出了基于量子密钥的弱盲签名协议，2010年他们又提出了基于量子秘密共享的强盲签名协议[19]。2011年陈永志等[20]提出了基于可控形态的代理弱盲签名协议。随后出现了一系列基于量子密钥的盲签名协议[21-27]。

本文提出了一种基于Bell态纠缠交换的盲签名协议，消息拥有者与签名者使用量子密钥分发技术共享密钥对消息进行加密，协议使用一次一密技术保证整个签名过程的绝对安全性。

1 准备知识

1.1 纠缠交换

四种Bell态粒子描述如下：

假设Alice拥有Bell态粒子|φ+〉12，Bob拥有|φ+〉34，经过Bell纠缠交换，量子系统变化为：

(1)

当对粒子1和粒子3执行Bell基测量时，粒子2和粒子4塌缩到对应的纠缠状态。比如Alice对粒子1和粒子3的Bell基测量结果为|ψ+〉13，则Bob对粒子2和粒子4的测量结果为|ψ+〉24。

1.2 量子逻辑操作

四种常见的量子逻辑操作(泡利操作符)表示为：

σ00=I=|0〉〈0|+|1〉〈1|σ01=σx=|0〉〈1|+|1〉〈0|σ10=iσy=|0〉〈1|-|1〉〈0|σ11=σz=|0〉〈0|-|1〉〈1|

以Bell态|φ+〉AB为例，经过泡利操作符作用后，量子态变化情况如表1所示。

表1 Puali操作与Bell态粒子的测量结果

2 量子盲签名方案

2.1 初始化阶段

(1) 消息变换：Alice将待签名消息m转换成二进制序列M=T2(m1,m2,…,mn)∈{0,1}n。T2代表一个二进制转换函数。

(2) 密钥共享：假定Alice是消息拥有者，Bob是消息确认者，Charlie是盲签名者。通过量子密钥分发技术(Quantum Key Distribution,QKD)，Alice与Bob秘密共享keyAB，Alice与Charlie秘密共享keyAC，Bob与Charlie秘密共享keyBC。QKD的物理安全特性保证密钥分发过程的绝对安全性。

(3) 粒子制备与分发：Charlie制备两串长度为n的Bell态粒子序列，n代表消息的长度。为方便描述，假定两串Bell态处于|φ+〉12和|φ+〉34(其余状态的签名过程类似)，Charlie按粒子下标将其分成序列P={S1,S2,S3,S4},其中Si代表两串Bell态中所有下标为i的粒子组成的序列。Charlie将S1S3发送给Alice，将S2发送给Bob，自己保留S4。

2.2 签名阶段

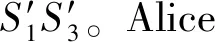
表2 二进制消息M经量子门转换后的变换情况

(2) 盲签名：Charlie收到EkeyAB(R1R3)后，使用Z基(|0〉,|1〉)或X基(|+〉,|-〉)对自己保留的S4进行测量，得到测量结果R4。Charlie使用keyBC加密R4和EkeyAB(R1R3)，得到EkeyBC(R4,EkeyAB(R1R3))。Charlie将EkeyBC(R4,EkeyAB(R1R3))发送给Bob。

2.3 验证签名阶段

(1) Bob接收了Charlie发送的加密序列后EkeyBC(R4,EkeyAB(R1R3))，使用keyBC解密后获得R4和EkeyAB(R1R3)，再使用keyAB解密EkeyAB(R1R3)获得R1R3；根据R4，Bob选择相同的测量基对S2进行测量，得到R2。此时Alice告知Bob她对消息M的绑定规则。

表3 验证规则

3 方案分析

3.1 无条件安全性

在本协议中，Alice与Bob、Charlie三方分别秘密共享的密钥都是通过量子密钥分配技术(quantum key distribution,QKD)在量子信道中完成分发的。量子密钥分配技术结合一次一密(one-time pad,OTP)在理论和实践中都已经被证明是绝对安全可靠的，因此密钥keyAB和keyBC以及keyAC均是绝对安全的。

如果攻击者Eve采用截获重发攻击(一种强有力的攻击方式)，量子的不可克隆性保证了Bell态粒子是不可被复制的，Eve对截获的粒子进行测量等操作势必会破坏Bell态粒子的纠缠关系，Alice签名信息相应会产生扰动，Charlie将拒绝签名；同理，三方均可以通过分析粒子纠缠关系以及检测量子信道等方式来检测是否存在窃听者。若发现窃听者存在，协议终止。需要注意的是，由于Alice通过泡利操作将消息编码在S1S3中，假设Eve侥幸避开检测，也得不到任何有用的信息。

3.2 不可伪造性

假设Alice或Eve是不诚实的用户，她们想伪造签名者Charlie来对消息进行签名，达到欺骗的目的。通过分析协议可以得知：keyBC是Charlie和Bob通过QKD和OTP进行安全保障的，Alice或Eve在不知道keyBC的情况下是不可能得到加密序列EkeyBC(R4,EkeyAB(R1R3))；与此同时，Charlie将自己对S4的测量结果R4也放在盲签名序列中，Alice或Eve无法得知R4的正确信息，因此本协议产生的盲签名是不可伪造的。

3.3 不可抵赖性

根据协议的描述，Charlie是无法否认自己的盲签名信息:Bob接收的加密序列使用的密钥必须为Bob与Charlie秘密共享的keyBC；同理，Charlie收到的加密序列EkeyAB(R1R3)必须由密钥keyAB加密，当Bob使用keyBC解密了EkeyBC(R4,EkeyAB(R1R3))后，只能使用keyAB才能解密出正确的R1R3，因此Alice也无法否认自己对消息的编码操作。

3.4 消息盲性

在本协议中，Charlie在执行签名的过程中，所有消息内容都是Alice通过keyAB加密的EkeyAB(R1R3)，Charlie无法在签名时获取任何和消息相关的内容。签名完成后，Alice与Bob的信息交换均不涉及原始的消息，而是通过对量子序列的操作。即Charlie无法将自己的签名与Alice的消息对应起来，达到了盲签名效果。

3.5 效率分析

量子签名协议的效率可以用如下公式计算：

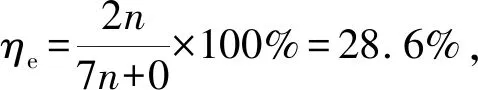
表4 效率分析

4 结 语

本文基于Bell态纠缠变换关系，提出了一个量子盲签名协议，消息拥有者对粒子序列执行泡利操作完成经典消息向量子消息的转变。三个参与方通过分别共享的量子密钥保证了协议的绝对安全性。通过方案分析可知本协议满足盲签名定义，通过效率分析可知完成n比特消息的盲签名，本协议的粒子效率为28.6%。由于现实通信环境的噪音等干扰因素，实际粒子效率可能偏低。