一种有效深度哈希图像拷贝检测算法

刘 琴 袁家政 刘宏哲 李 兵 王佳颖 叶 子

1(北京联合大学北京市信息服务工程重点实验室 北京 100101)2(北京开放大学科学研究处 北京 100081)3(中国科学院自动化所模式识别国家重点实验室 北京 100190)4(国网通用航空有限公司科技信息部 北京 102209)

0 引 言

近年来很多图像经非法合成、复制剪切等一系列篡改后发布到网上，这一行为侵害了持有者的权益。为了保护图像的版权，提出了拷贝检测这一积极有效的保护策略。拷贝图像通常是在原图基础上经过光学变换、几何变换等转换而来，它们语义一致、画面近似且来源相同。由于图像处理软件如美图秀秀、天天P图的兴起，用户不需要专业的图像处理知识也能够对图片进行这些操作，使得拷贝图像的数量以指数级增长。因此要在大规模图像数据中寻找拷贝图像，算法的精度和效率是亟待解决的难点。

哈希作为提升检测效率的有效手段，在解决大规模的计算机视觉问题中受到了重视。很多学者提出了面向拷贝检测的图像哈希算法，主流做法是依赖传统的特征描述符算子如SIFT[1]、HOG[2]、GIST[3]、LBP[4]、HSV[5]等手工提取图像单一特征或者融合特征，然后经过哈希函数的转化，压缩为一定数目的二进制编码序列即哈希码，再将学习得到的哈希码作为图片特征用于拷贝检测。但上述方法已经无法满足当前大数据时代下高精度的需求了。近年来，基于深度学习的哈希算法[6-10](简称“深度哈希”)由于其优秀的表征能力，在大规模图像相似性检索上得到广泛应用。因此本文提出一种端到端的基于深度哈希的新型图像拷贝检测算法(copy detection based on deep hashing,DHCD)。该算法通过同时学习图像对的深度特征和哈希码特征，弥补了传统图像哈希方法中特征提取与哈希映射独立进行的缺陷。并且设计了在线挖掘难分样本的策略，提升了模型的识别精度。实验表明，DHCD算法对多种形式的拷贝攻击都具有鲁棒性，与当前拷贝检测中的图像哈希方法相比在准确率上取得了很大的优势。

1 相关工作

现有的面向拷贝检测的图像哈希算法一般步骤是先提取图像特征，再学习哈希码。总结来说，可以分为两类：基于变换系数的哈希和基于图像视觉特征的哈希。

基于变换系数的哈希方法主要是将空域的图像数据转到频域中去。2003年Kim[11]提出图像分块结合离散余弦变换(Discrete Cosine Transform,DCT)的图像拷贝检测算法，其将图像分成矩阵块，然后计算矩阵块离散余弦变换后的交流系数,利用此系数作为图像的哈希码来计算距离。杨帆[12]以DCT变换、离散小波变换(Discrete Wavelet Transformation,DWT)和主成分分析(Principal Component Analysis,PCA)等技术为嵌入点研究感知哈希算法。Srivastava等[13]提出一种基于图像统计特征的图像哈希技术，该算法对预处理后的图像进行Radon变换，对生成的每一列的系数进行DCT变换，最后取每一列的第一个系数构成行向量，用于提取均值、标准差、峰度和偏差四个统计特征来构建哈希码。以上算法对常见的保持图像视觉内容不变的数字处理具有良好的鲁棒性，对不同内容的图像具有较好的唯一性，但是对旋转和图像局部内容的改变不鲁棒。

图像视觉特征主要有颜色、纹理、形状和空间关系等特征。Ling等[14]首先获得一系列不同尺度的SIFT特征描述符，采用基于熵最大化的二值化方法将描述编码二值化，构建哈希码。马庆贞等[15]在局部保持投影算法基础上加入了正则化项，将高维GIST特征映射到低维空间的同时避免了过拟合，并且基于最大熵模型将低维特征映射到汉明空间得到哈希码。杜根远等[16]提出了一种数据感知哈希方法，该算法首先根据HSV(Hue,Saturation,Value)特征数据的局部结构将重建误差和映射误差结合起来，构建优化目标函数并学习出哈希函数。郑丽君等[17]提取SIFT特征点二维位置信息，通过计算各个特征点与图像中心点的距离、角度，分块统计各区间的特征点数量，依据数量关系量化生成二值哈希序列。沈麒等[18]提出一种基于CS-LBP(Centrally Symmetric Local Binary Pattern)纹理与位图像统计的图像哈希算法，将所有的低频和高频特征联合起来生成图像哈希序列。基于图像视觉特征的哈希算法中GIST和HSV是全局特征，不受图像旋转和平移的影响，但是对图像局部区域的方向、大小等变化敏感，SIFT和LBP特征属于局部特征，对方向具有尺度旋转不变性，但计算量大，且不能很好地抵抗JPEG(Joint Photographic Experts Group,JPEG)压缩攻击。

以上两类方法的性能都非常依赖于所提取的图像特征以及线性映射的函数功能，因此学习得到的哈希码特征仍是浅层的基于手工设计的特征，在实际场景下对复杂语义信息的处理不够强大，并且不能很好地应对所有变换形式。与人工设计的特征相比，卷积神经网络(Convolutional Neural Network,CNN)更能获得图像内在特征，已在图像分类、图像分割、目标检测方面都获得了很好的性能。

深度哈希算法则结合了卷积神经网络自我学习的优势以及哈希方法在检索中计算效率和空间上的优点，通过训练卷积神经网络模型，将网络输出的结果约束在一个范围内，例如[-1,+1]，量化得到最终的哈希码，用哈希码来代表图像特征。因此本文将深度哈希应用到图像拷贝检测领域，充分利用了深度网络强大的学习能力和哈希码在检索上的优势，并且针对拷贝检测任务做了具体的改进。DHCD算法在大规模图像数据的拷贝检测中既保持了高效又达到了高精度。

2 DHCD算法原理

DHCD算法模型的框架如图1所示，其中子网络1(Network1)和子网络2(Network2)是完全相同且权重共享的两个网络。每个子网络中有两个重要的模块，一个是特征提取网络FEN,一个是哈希码学习网络HLN。下面将对DHCD算法各个模块作详细介绍。

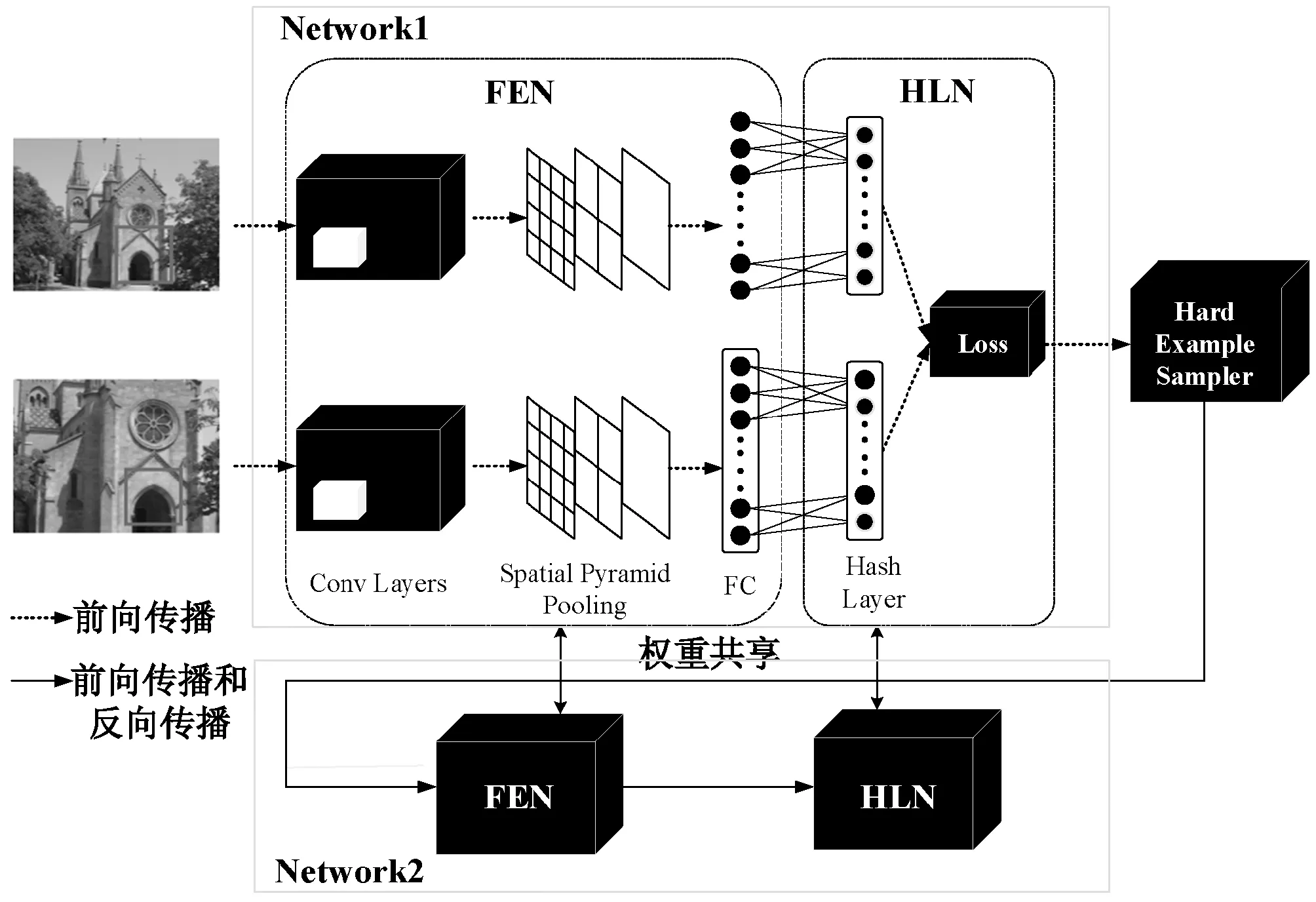
图1 DHCD算法模型框架

2.1 特征提取网络

特征提取网络模块是基于权重共享的多尺度孪生卷积神经网络结构[19]。该模块以一对图片和标签为输入，先后经过卷积模块(Conv Layers)、空间金字塔池化层(Spatial Pyramid Pooling,SPP)和全连接层(Fully-Connected layer,FC)得到该图片的高维特征向量。其中，Conv Layers中拥有4个卷积层，3个池化层。每一个卷积层后面都接了Rectification Linear Unit(Relu)激活函数。特征提取网络框架的参数配置以如下形式描述：“Conv”表示卷积层，“Pool”表示池化层，“filter”表示卷积层的卷积核的数目和尺寸，以格式“num x size x size”表示，其中“stride”表示步长，“pad”指在输入的每一边上加上多少个零值像素，“kernel”表示卷积核的大小，“LRN”表示这里运用了局部响应归一化层(Local Response Normalization,LRN)，即对一个局部的输入区域进行归一化，“pyramid_height”表示金字塔的高度，“500”表示全连接层FC的输出维度。具体网络模型配置如表1所示。

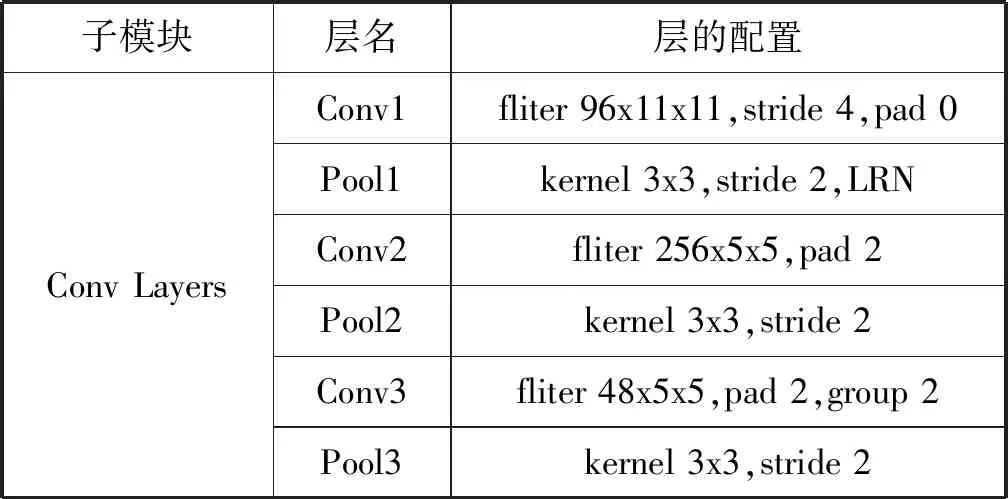
表1 特征提取网络框架参数

拷贝数据集中含有多种尺度变换，如裁剪、旋转等。传统CNN结构中全连接层需要固定输入维度，因此基本的做法是将输入图像缩放成固定尺寸，但这一做法对于拷贝数据集而言会引起图片失真从而带来精度损失。本文引入的空间金字塔池化层[20]改变了传统CNN结构中对于固定输入图像尺寸的要求，可以接受任意尺寸的图像为输入，当输入图像为整幅图像时，则在一定程度上减少了信息的损失。在Conv Layers最后一个卷积层和第一个FC全连接层中间接入金字塔池化层。如图2所示，金字塔池化层的每一层都将上一层卷积层Conv4的特征图分成不同的块，对每一个块进行池化，特征图的维度保持不变，这样一来，就可以将任意尺寸的图像对应的特征图转化为固定维度的输出。这种分层池化的方式使得学习得到的图像特征更加鲁棒。本文构建了三层金字塔，即有三种不同大小的划分刻度，分别是4×4、2×2、1×1，具体结构如图2所示。

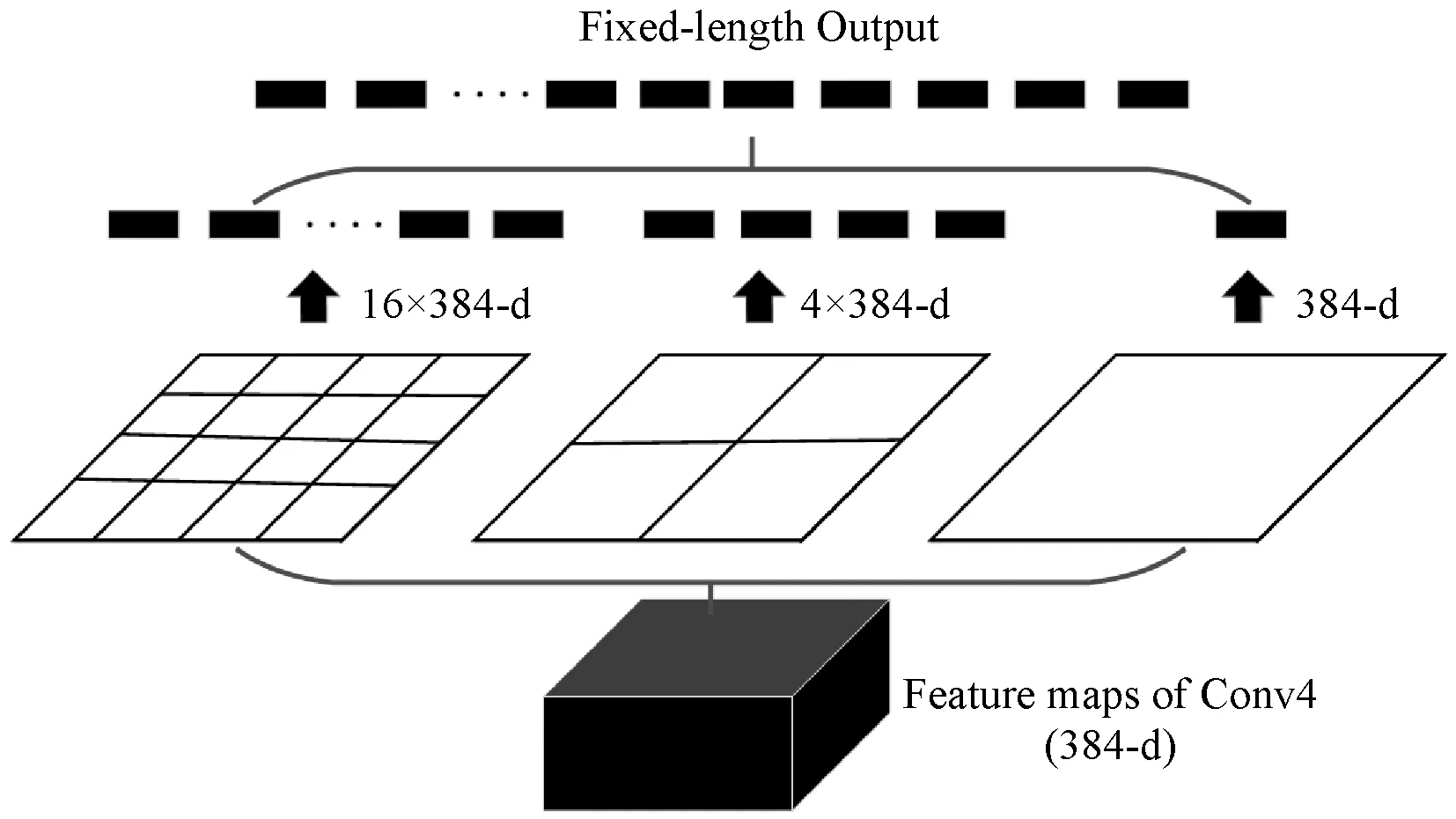
图2 空间金字塔池化过程

2.2 哈希码学习网络

哈希码学习网络以特征提取网络最后一层的输出为输入，哈希层的输出(类二值码)为模型最终输出。其中，“哈希层”实为全连接层，它将特征提取网络输出的500维图像特征映射成k维(k一般为12，24，36，48等)哈希特征，且尽可能保证该k维特征在[-1，+1]区间内。得到该k维哈希特征后，使用符号函数对其进行量化，使其特征值全为{-1,+1}。

将哈希层的输出记为U，每次批量迭代处理的图像对为N，U={uij|i=1,2,…,N,j=1,2}，uij表示第i对样本中第j个样本的输出。yi表示第i对样本的标签，1表示拷贝，0表示非拷贝。因此可以得到如下公式：

(1)

通过对式(1)取负对数似然，可得损失：

(2)

当yi=1时，拷贝样本的损失尽可能小，当yi=0时，拷贝样本的损失尽可能大。但哈希层的最终目标是学习出类似于二值码的输出，使得uij的取值尽可能趋向于{-1,+1}k，因此引入L1正则化项，得到的总损失如下：

(3)

在此目标函数的基础上，利用小批量梯度下降法对网络进行反向传播。由于绝对值运算在某些点上是不可微的，因此计算的是L中每一因子项的梯度，式(3)中损失函数两项因子的次梯度求解公式如下：

(4)

得到类二值码uij以后，利用sgn(uij)来进行量化，得到真正的哈希码bij。sgn(uij)的表达式如下：

(5)

2.3 难分样本挖掘

一些经过了强烈变换的拷贝图片(正样本对)在训练过程中很容易被误判为非拷贝图片，一些在视觉特征上很相似的非拷贝图片对(负样本对)也容易被误判为拷贝图片对，这些便是难分样本。而其他的如经过普通旋转、简单裁剪等变换或者视觉特征差距很大的图片对则很容易被模型判别正确，即为简单样本。

挖掘难分样本是针对训练过程中导致损失值很大的一些样本(即使得模型很大概率分类错误的样本)重新训练它们。图1所示的框架中用两个子网络来实现这一策略。先将初始数据集送入子网络1，由虚线箭头表示，只进行前向传播，不更新每一层网络的权重。计算出每个训练批次中图片对的哈希损失值(Loss)后，将损失得分大的正样本对和负样本对按照1∶3的比例送入难分样本采样器(Hard Example Sampler)中。当难分样本采样器中的样本对达到了一个训练批次的数量时，则送入子网络2，重新进行训练，并根据式(4)进行反向传播，由实线箭头表示。由于两个子网络权重共享，子网络2和子网络1的参数同时更新，从而达到了在线挖掘难分样本的效果。

2.4 整体算法流程

输出：哈希码{+1，-1，+1，-1,…，+1}。

初始化：模型中所有权重和偏差用均值0和方差0.01的高斯分布来初始化。

训练阶段：

子网络1:

1. 将成对训练样本批次送入特征学习层，根据前向传播获得图像特征。

2. 特征经过哈希层，得到类二值码ui1、ui2。

3. 根据式(3)计算损失L，将正负样本对中的难分样本按照1∶3的比例送入采样器。

4. 重复步骤1-步聚3，直至网络收敛生成模型。

子网络2：

当采样器中的样本达到一个训练批次的数量时送入网络2，当特征经过哈希层时，根据式(3)计算损失L，并进行反向传播，更新权重。反向传播公式如式(4)所示。

测试阶段：

利用训练阶段生成好的模型提取测试样本的特征，只需取子网络1权重共享的孪生卷积神经网络结构中任意一路网络结构进行前向传播，将得到的类二值码特征二值化B=sgn(u)，即得到每个样本的哈希码特征。

3 实 验

为了验证DHCD算法的有效性，在拷贝数据集上进行了性能评估与测试，并与现有方法进行对比。实验是在带有Intel Xeon E5-2650 v4处理器，131GB RAM，TITAN XP(Cuda-8.0.61，CuDnn v5.0)的服务器上使用深度学习框架caffe实现的。训练过程中初始学习率设置为0.000 1并且每15 000次迭代后下降10%，动量为0.9，权重衰减项设置为0.000 5，损失函数中η的值设为0.01。

3.1 数据来源

网上公开的图像拷贝数据库有INRIA Copydays数据集[21]、CoMoFoD数据集[22]、Image Manipulation数据集[23]、MICC-F220和MICC-F2000数据集[24]。这些数据集包含了不同的攻击形式，例如旋转、裁剪、平移、缩放、模糊、噪声等，如图3所示。

图3 INRIA Copydays数据集示例

由于这五个数据集数据量很小，因此本文为了扩大数据集和增加数据集的复杂性，从ImageNet数据集中10 00个类各取20幅图片，每幅图片模拟生成10种拷贝变换，变换形式有：垂直翻转、水平翻转、向左上平移、向右下平移、添加文字、向右旋转45度、向右旋转90度、裁剪、画中画、高斯模糊，如图4所示。在这里，本文将模拟生成的数据集称为ImageNet-CD。

图4 ImageNet-CD模拟攻击形式

最后将以上数据集进行组合，其中拷贝图片对的组成与分布如表2所示。拷贝图片对来源于原始图片和其拷贝图片(变换种类)的组合，共225 284对正样本。负样本来源于从以上数据集中随机选取的没有拷贝关系的图片对，共274 916对。综上，正负样本对共组成500 000对图片，按照3∶1的比例分成训练集和测试集。

表2 拷贝图像对(正样本)的组成与分布

3.2 评价标准

拷贝检测的目的是检测出有多少拷贝样本对被正确识别。本文认为汉明空间内，哈希码距离在1以内(小于等于1)的图片对为拷贝图片。24维则是汉明距离为2以内图片对为拷贝图片对，后面依次类推，分别为36维对应距离4，48维对应距离6。拷贝图片对的类别标签为1，非拷贝图片对的类别标签为0。由于测试集中正负样本比例接近于1∶1，因此本文的评价指标准确率定义为：Accuray=正确识别的样本对/总样本对。

3.3 实验结果与分析

3.3.1微调影响网络性能的评估

本文按照图1所示模型结构从头训练了哈希层输出为{12,24,36,48}维类二值码特征的模型。例如对于12维生成模型，提取哈希层特征后经过量化得到12维哈希码。但对于这些不同维度的模型而言，特征提取网络部分学习到的特征都是相同的，维度发生改变的只有哈希层，因此从头训练严重浪费了提取深度特征所花费的训练时间。为了克服这一缺陷，本文对模型进行了微调。具体做法是{24,36,48}维模型利用已经训练好的12维生成模型进行微调，将哈希层的权重w和偏置项b的学习率分别扩大了10倍。从表3中可以看出，微调后的模型准确率普遍高于从头训练生成的，这说明由于加入了之前已经训练好的模型的参数经验，模型获得了比从头训练更好的性能。另外，从表3中可以看出24维的模型的准确率最高，随着哈希码维度的上升，准确率并没有大幅提升，而是微有下降，这说明哈希层参数越大，过拟合的风险越高。因此哈希层维度为24且经过了微调的模型的准确率最高。

表3 从头训练和微调

3.3.2多尺度特征影响网络性能的评估

为了验证多尺度提取到的特征更适用于拷贝数据集，本文做了对比实验。实验中保持其他设置一致，都是在经过了微调的24维哈希模型上进行的。表4给出了选取不同池化层数和池化方式对于模型准确率的影响。其中0层表示在这里没有使用空间金字塔池化层，即将初始数据集中的图片对的尺寸统一缩放到227×227像素，并且在Conv层后接的是普通的池化层。2～5层则是在输入层将图片对以任意尺寸(在这里是以原图尺寸)送入网络模型中训练。可以看出，选择了2～5层空间金字塔池化的模型普遍高于0层的模型，即提取多尺度特征更适用于拷贝检测任务。另外3层的金字塔加平均池化，取得了较好的结果。这是因为当空间金字塔层数较少时，最大池化会比平均池化损失更多的特征信息。

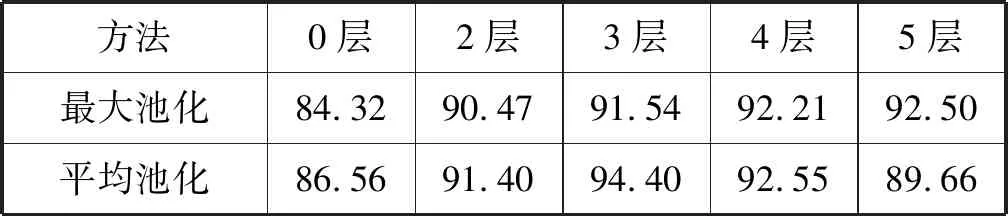
表4 选择不同的空间金字塔层数时的准确率,

3.3.3挖掘难分样本影响模型性能的评估

在挖掘难分样本时，训练过程中小批量尺寸设置为127，Sampler将在每一轮迭代中将哈希层高损失的正样本对和负样本对按照1∶3的比例收集起来。无难分样本挖掘的实验设置是只对子网络1进行训练，既有前向传播也有反向传播。从图5可以看出，当迭代到100 000次时，测试集的损失接近于训练集损失，且损失值接近0.01。而图6中测试集的损失远大于训练集的损失。显然图5模型的收敛性优于图6。从表5的结果中也可以看出，经过了难分样本挖掘的模型的准确率较未经过挖掘的模型提高了6.1%，因此在拷贝检测任务中挖掘难分样本，可以提升模型对难分样本的识别效果，能更有效地区分出拷贝和非拷贝样本对。

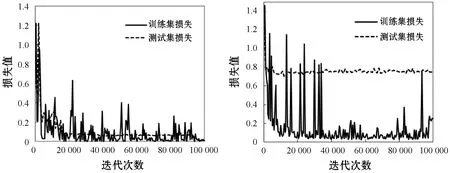
图5 有挖掘难分样本的模型损失(24维) 图6 无挖掘难分样本的 模型损失(24维)

表5 挖掘难分样本对性能的影响

实验网络结构准确率/%无难分样本挖掘子网络190.40有难分样本挖掘子网络1+子网络296.50

3.3.4不同形式攻击下的准确率

图7列出了本文算法对不同形式攻击的敏感性。攻击程度1～7分别表示裁剪百分比为5%、10%、20%、40%、50%、70%、80%；JPEG压缩因子为3、5、10、20、30、50、75；旋转角度为10%、30%、45%、60%、90%、120%、135%；添加字幕和画中画以及强烈变换则是依次增加复杂度。从图7中可以看出，本文模型学习到的深度特征对于裁剪、旋转、JPEG压缩、添加字幕的攻击形式鲁棒，对于中等程度的画中画和强烈变换攻击形式较为鲁棒，说明了模型整体效果良好，学习到的哈希码质量较优。

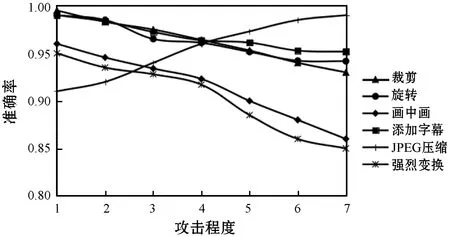
图7 不同形式攻击下的准确率

3.3.5与其他哈希方法进行对比

目前应用在图像拷贝检测上的哈希方法有LSH[25]、ITQ[26]、MLH[27]、SKLSH[28]等，本文分别与以上方法在不同哈希码维度上进行了准确率和效率的比较。在这里为了统一，传统图像哈希方法的具体实现是首先提取本文测试集的512维GIST特征，然后分别利用上述哈希函数进行哈希码学习。本文算法则是任选模型中一个子网络的一路网路结构来提取测试集的哈希码特征。距离的计算方式都是汉明距离。对比结果如表6所示，可以看出，DHCD算法比传统图像哈希方法提升了10%左右的准确率，生成的哈希码更能精确地区分出拷贝图像和非拷贝图像。这是因为传统的图像哈希方法基于手工设计的特征更倾向于描述图像的视觉信息，而不是其语义信息，而且特征的学习和哈希函数的学习两个阶段是割裂的，会导致产生的二值码特征与特征表示不符。而深度特征对于平移、旋转、扭曲、比例缩放等变化都有着高度的鲁棒性，且本文所提算法模型采用的是端到端的训练方式，能同时进行特征学习和哈希码的学习。因此本文基于深度哈希的模型在图像表示上的性能是优于基于传统图像哈希方法的。

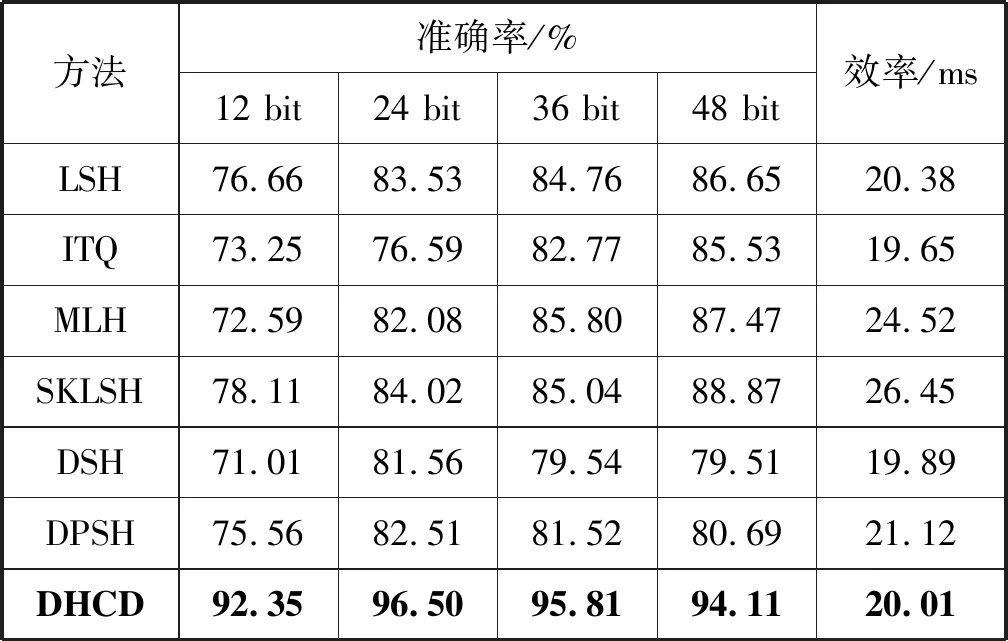
表6 与其他哈希方法在准确率和效率上的比较

另外，本文还与常见的应用于图像相似性检索的深度哈希方法进行了对比，如DSH[7]、DPSH[8]。从表6中可以看出，拷贝检测不同于相似性检索，针对拷贝检测任务特殊设计的模型和策略将大大提升检测的精度。

同时为了验证DHCD算法在效率上依然保持了哈希的优势，本文将以上所提算法在24维哈希码上进行了效率对比，即计算上述算法提取一幅图片的24维哈希码特征的前向传播耗时。从表6中可以看出本文方法在效率上和其他哈希方法不相上下，没有增加耗时。

4 结 语

本文提出了一种有效的深度哈希图像拷贝检测算法DHCD来实现拷贝检测对于高精度与高效率并存的需求。该算法利用深度网络来学习图像对的哈希码，在有监督信息的条件下，网络组件之间相互反馈，所学习到的哈希码的表征能力远远优于传统图像哈希方法。此外，针对拷贝数据集的特殊性，本文设计了多尺度特征提取以及难分样本挖掘策略，提升了DHCD算法对于不同拷贝攻击形式的鲁棒性。在扩展组合而成的拷贝数据集上的实验结果表明，DHCD算法的准确率比其他哈希方法提升了近10个百分点，且效率上仍具有优势。因此，面对海量高维图像数据，本文算法具有很好的实际应用价值。未来将设计出更优的哈希损失函数来匹配拷贝检测任务。