空间失稳目标线阵成像畸变分析与三维重建
李荣华,王振宇,陈 凤,肖余之,薛豪鹏
(1. 大连交通大学机械工程学院,大连 116028;2. 上海宇航系统工程研究所,上海 201109)
0 引 言
太空垃圾又称空间碎片或轨道碎片,是指围绕地球轨道的无用人造物体。太空垃圾小到由人造卫星碎片、漆片、粉尘,大到整个飞船残骸构成。其中大型太空垃圾(卫星由于故障或任务结束而被放弃)不但占用其原在的有限轨道资源,还对其他航天器的安全造成不可估计的危害。为解决这一问题,各国陆续开展了对失效卫星的环绕检测、运动跟踪、交会对接、在轨维修等操作[1-4]。而实现这些目的,就必需获取非合作目标的三维空间信息,进行三维模型重建。激光雷达由于其受光照和距离等因素影响小,抗干扰能力强等优点,是目前监测空间目标较为理想的工具,常见的成像方式为线阵式与面阵式[5]。
面阵式激光雷达[6]采用多束密集的激光束直接向各个方向漫射,最大优势是能够快速记录整个场景,避免了扫描过程中目标或激光雷达移动带来的各种问题。但对远距离空间运动,面阵式成像分辨率低,对目标的测量精度仍然不能满足测量要求。线阵式激光雷达在空间作业中,相较于面阵式负载较小,成像分辨率高,获取的线阵数据同样能够用于运动参数估计及三维模型重建。对于静态目标,已知目标与雷达相对运动信息,运用线阵式激光雷达获取不同时刻线阵数据,可直接组合线阵信息得到测量目标的三维模型;但对于运动目标,目标位姿一直处于变化状态,不同时刻获取的是当前时刻目标扫描位置线阵数据,扫描数据存在畸变,所测量的运动目标轮廓与目标的实际外形相比一般会存在形变,直接组合线阵信息并不能准确地对被测目标进行三维重建。对于非平衡(失稳)状态下,蔡银桥等[7]对星载三维激光雷达图像畸变进行研究,研究了在不同扫描周期内三维激光雷达图像变形,得出了控制成像时间是降低图像畸变的关键因素。针对线阵畸变对目标方位估计性能的影响,李建等[8]通过理论、仿真以及试验数据处理等方面进行分析,并提出了一种初步的阵形校正方法。
解决运动目标线阵扫描中存在的畸变问题,主要分为合作目标与非合作目标两种情况下进行分析[9-10]。对于合作目标,即目标运动参数已知或目标可添加标记,赵竹新等[11-12]给出了一种利用线阵相机立体交会测量弹丸设计,根据弹丸目标的外形特点设计了一种新的标记线方法,避免了线阵相机扫描速度不足而难以实现弹道同步测量的难题。高俊钗等[13]根据线阵相机图像采集特点,以标准圆形作为标定目标确定了物像关系和校正插值系数,并设计线性插值算法进而能够对任意形状的目标进行成像校正。在合作模式下,被测目标运动估计精度通常能够达到要求,但是对于无法进行标定的测量目标或者无法增加辅助设备的测量情况并不适用。对于非合作目标,王盈等[14]提出了一种适用于复杂空间目标的在轨激光雷达成像仿真流程,并强调了面积法在复杂目标成像可见判断方面的适用性,适用于大表面目标测量。本课题组前期通过相邻两次扫描的畸变点云配准来获取测量目标的瞬时运动参数,该方法仅使用单一载荷实现了非合作空间目标相对位姿的测量,但是仅能估算自旋状态的空间失稳目标,对于复杂运动的空间失稳目标或者两次获取点云重合量达不到配准要求的情况有待进一步研究。
综上所述,本研究以实现空间失稳目标三维重建为目的,针对空间失稳目标,因其非合作性、形状多样性、运动状态不确定性,且线阵扫描式激光雷达测量动态目标发生畸变而无法精确恢复目标三维模型问题,首先对扫描畸变从测量角精度与测距精度两大判定条件进行分析,然后根据测量工况对目标点云进行带畸变配准。该方法不仅能够有效解决空间失稳目标线阵成像畸变问题,而且可以实现较高精度的动态非合作目标三维重建,为线阵式测量技术进一步发展提供新的研究方向。
1 线阵激光雷达畸变分析
1.1 畸变产生原因
线阵扫描型激光雷达在探测失稳目标过程中,会发生时空非定常点云数据畸变,所扫描的运动目标数据与目标的实际模型相比会存在差异。这种差异是由于线阵雷达的扫描等效速度与目标运动速度不一致所导致的。所谓的线阵雷达的扫描等效速度是指线阵雷达单个像素的宽度与扫描频率的乘积,比如传感器的单个像素宽度为0.001 mm,扫描频率为100k 线/s,则扫描等效速度为1 m/s。当雷达的扫描等效速度与目标的运动速度相等时,目标的线阵成像与目标的实际模型一致;当雷达的扫描等效速度大于目标的实际运动速度时,目标的线阵成像与其实际目标模型相比显得被拉伸了,相反,当雷达的扫描等效速度小于目标的运动速度时,目标的线阵成像与其实际目标模型相比显得被压缩了。运动目标线阵成像的这种特点,从成像效果看,是一种成像失真。如图1所示,假设目标总共需要线阵雷达单程扫描8次,奇数次雷达扫描方向与目标运动方向一致,雷达的扫描等效速度小于目标的实际运动速度,目标表面同向压缩;偶数次雷达扫描方向与目标运动方向相反,雷达的扫描等效速度大于目标的实际运动速度,目标表面反向拉伸。最终导致线阵雷达扫描运动目标后产生不容忽视的畸变误差。
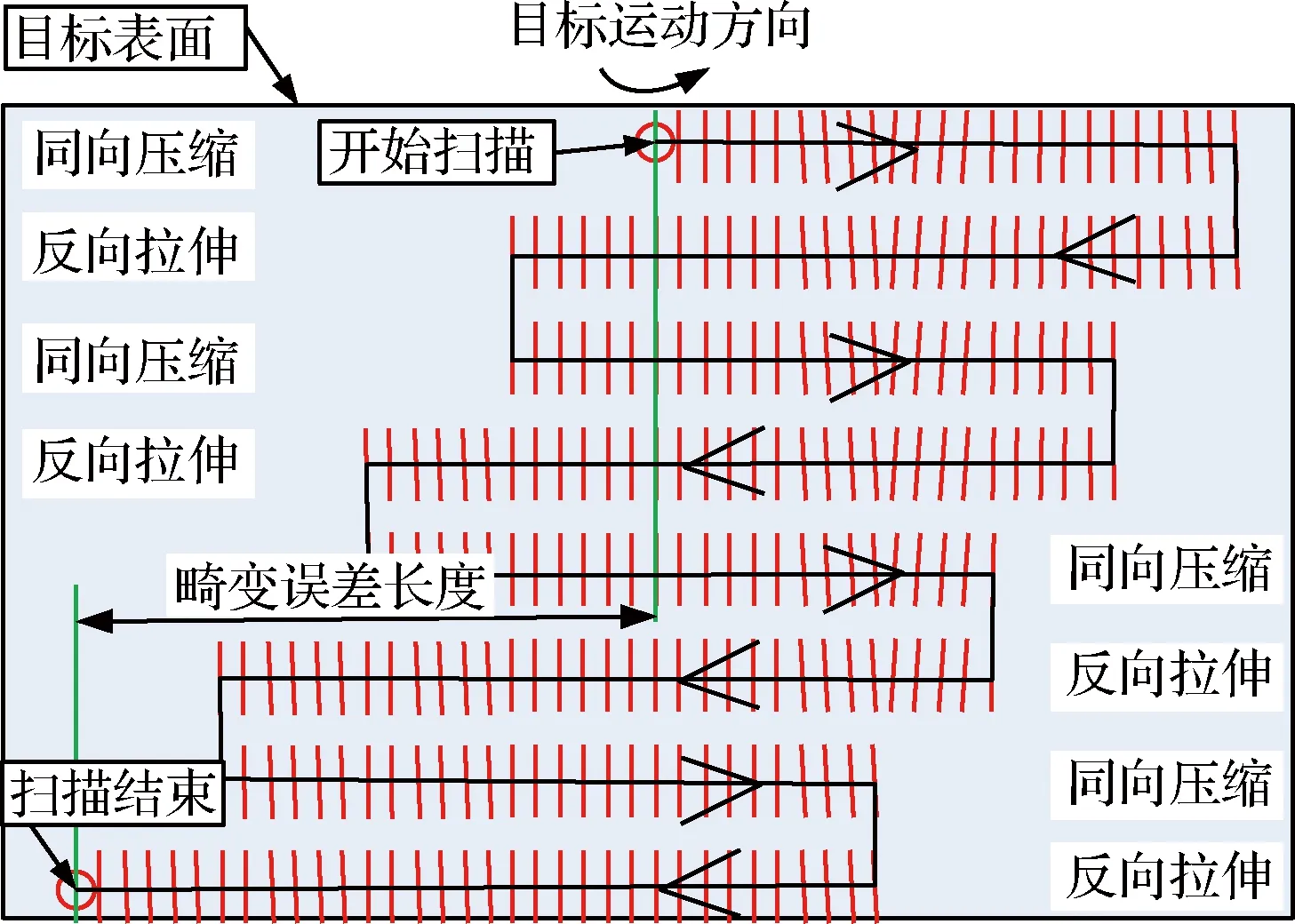
图1 目标表面扫描畸变产生示意图
1.2 畸变容忍度临界值
因为线阵扫描雷达受扫描棱镜加工精度影响,角分辨率大小会出现周期性变化,所以即使目标是静止状态,线阵雷达测量的点云也会出现畸变。由此可见,当目标受运动影响出现的畸变大小如果不大于雷达自身测量精度,则恢复畸变的过程将失去意义;反之,如果运动畸变大于雷达测量畸变,则有理由认定为目标失稳,需要畸变补偿。此外,由于受雷达角分辨率精度影响的畸变程度无法通过叠加来判断,而且考虑到为了提高畸变恢复效果及重建精度,以雷达测角精度为参考的失稳临界值向下降低一个数量级。
以雷达测量精度为衡量基准计算目标畸变容忍度临界值,即当目标由于运动导致的数据畸变程度超过了雷达自身测量精度的10%(降低一个数量级)时的目标运动速率认为是畸变容忍度临界速率。现从雷达测角精度与测距精度两方面对畸变容忍度临界值进行判定。
1.2.1角精度判定条件
当畸变容忍角度为r时,根据雷达指标:雷达环绕测量分辨率为m×n=400×400,线扫描宽度为Ls=50,单方向扫描次数为m/Ls=8,单次扫描时间为t=100 ms=0.1 s。可以推算出相邻点扫描所花时间t′=3.125×10-5s:
(1)
重建所能容忍的相邻点间畸变角度临界值r为激光雷达测角精度(30″),即r=30″,则目标失稳临界自旋速率ωr=26.6667(°)/s:
(2)
目标畸变容忍度临界自旋速率为ω=26.6667(°)/s;即当目标自旋速率大于该值时,即使忽略雷达测角精度,章动的复合运动的角重建误差也会超过指标。
1.2.2测距精度判定条件
假定已知信息:目标自旋角速率为ωm=12(°)/s,章动角速率为ωz=2.5(°)/s,雷达视场角为20°×20°,目标与雷达工作距离为L=80 m,成像分辨率为m×n=400×400,目标主体参数为2.000 m×3.500 m×2.500 m,雷达测距精度为dm=0.05 m。目标章动方向和自旋运动方向在某一时刻同向时,目标表面一点达到最大的运动角速率ωmax=14.5(°)/s:
ωmax=ωm+ωz
(3)
考虑最大畸变情况,对下面两种情况分别计算。
1)目标运动方向与扫描方向平行时
目标运动方向与扫描方向平行时,雷达扫描运动示意图如图2所示,根据雷达扫描距离L=80 m,雷达视场角为20°×20°,可得X轴单方向雷达最大扫描距离为LX=28.212 m(Y轴方向同理):
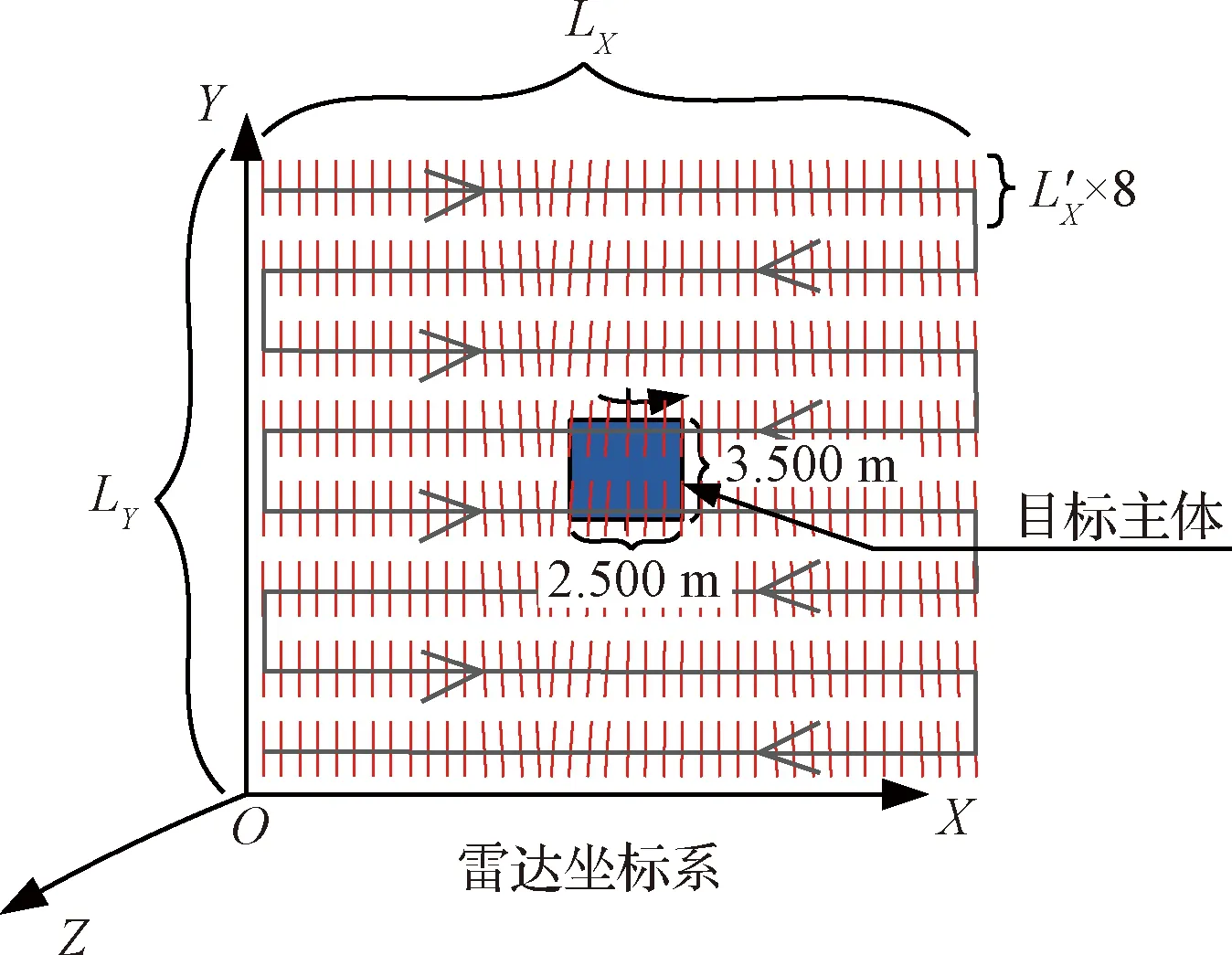
图2 平行时雷达扫描运动示意图
(4)
X轴单方向扫描次数为m/Ls=8,则单次扫描距离L′X=3.527 m:
L′X=LX/(m/Ls)
(5)
目标主体参数中宽度3.500 m与高度2.500 m均小于3.527 m,因此雷达扫面目标主体扫描一次或两次。当雷达扫面目标主体扫描两次时,用时最长,且畸变最大。最大用时tmax=0.014 s:
tmax=(1+3.500/28.212)t/8
(6)
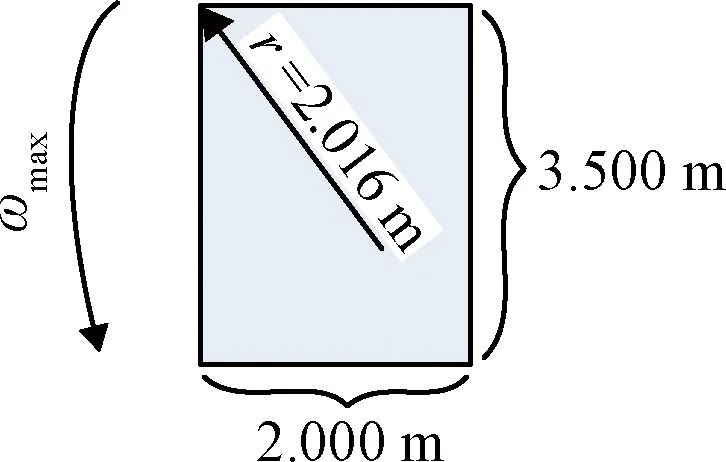
图3 目标运动半径
如图3所示,目标运动半径r为:
(7)
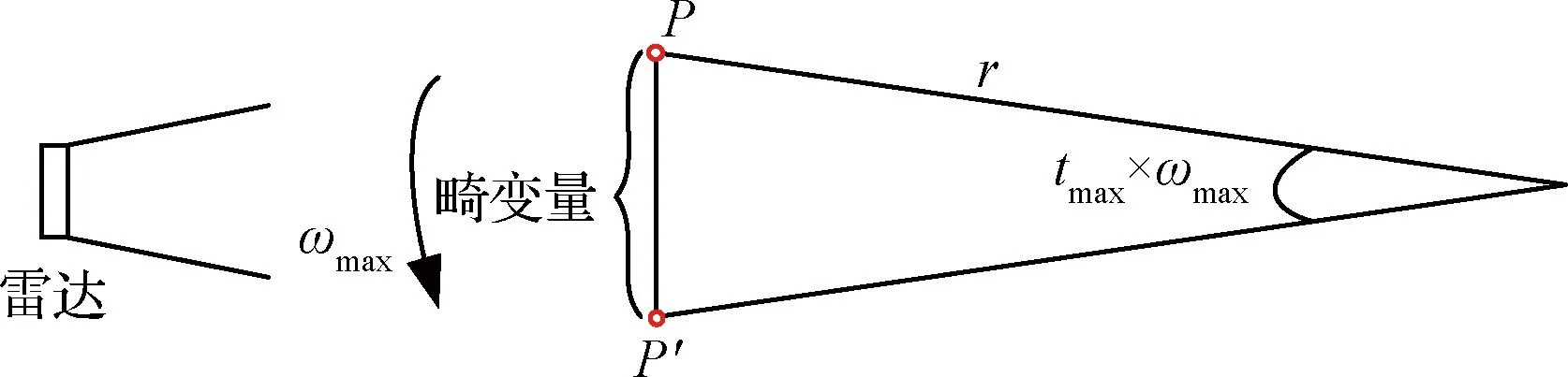
图4 目标表面点畸变量示意图
图4中,目标表面P点为真实位置,P′为畸变位置。畸变量Ldis=0.0071 m:
Ldis=2rsin(tmaxωmax/2)
(8)
计算显示:在畸变最大的情况下,表面一点P的畸变量为0.0071 m,而雷达测距精度小于等于0.05 m,因此畸变可忽略。
2)当目标运动方向与扫描方向垂直时
当目标运动方向与扫描方向垂直时雷达扫描运动示意图如图5所示。
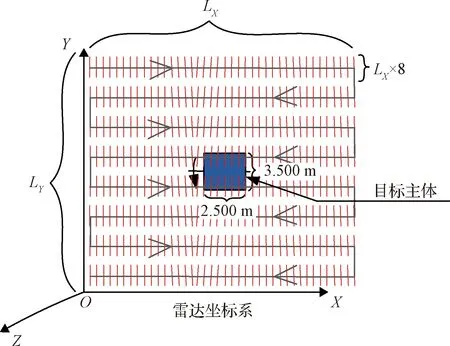
图5 垂直时雷达扫描运动示意图
同理当目标运动方向与扫描方向平行时,可得目标运动方向与扫描方向垂直状态畸变量Ldis=0.0071 m:
Ldis=2rsin(tmaxωmax/2)
(9)
计算显示:在畸变最大的情况下,表面一点P的畸变量为0.0071 m,而雷达测距精度小于等于0.05 m,因此畸变可忽略。
3)根据测距精度计算最大运动速度容忍度ωr
根据测距精度0.05 m,畸变影响在10%获得失稳速率临界:
ωr=2arcsin(0.05×10%/2/r)/tmax=10.15(°)/s
(10)
若章动为2.5(°)/s,自旋速率最大容忍度为7.65(°)/s。
1.3 临界值判定
综合两种临界值判定条件:根据角精度判定条件,目标畸变容忍度临界自旋速率ω=26.6667(°)/s;根据测距精度判定条件,当目标运动方向与扫描方向平行与垂直两种状态下,畸变量均低于测距精度一个数量级,且根据测距精度,目标畸变容忍度临界自旋速率ωr=10.15(°)/s。在本测量系统已知数据下,结合费马引理,目标畸变容忍度临界自旋速率取极大值,即ωr=26.6667(°)/s。当目标自旋速率大于等于ωr时,初次配准时需要对点云数据进行畸变恢复;当目标自旋速率小于ωr时,初次配准时对点云的畸变恢复将失去意义。
2 带畸变点云配准
2.1 坐标系建立
目标坐标系坐标原点设为待测目标几何中心位置,ZO轴方向设为待测目标自旋轴方向,YO轴方向设为太阳翼中轴线方向,基于右手法则确定XO轴方向。雷达坐标系以雷达中心为坐标原点,环绕检测半径设为80 m,三轴方向与初始获取目标反馈信息的方向一致。世界坐标系与雷达坐标系重合,扫描工况笛卡尔坐标系如图6所示。
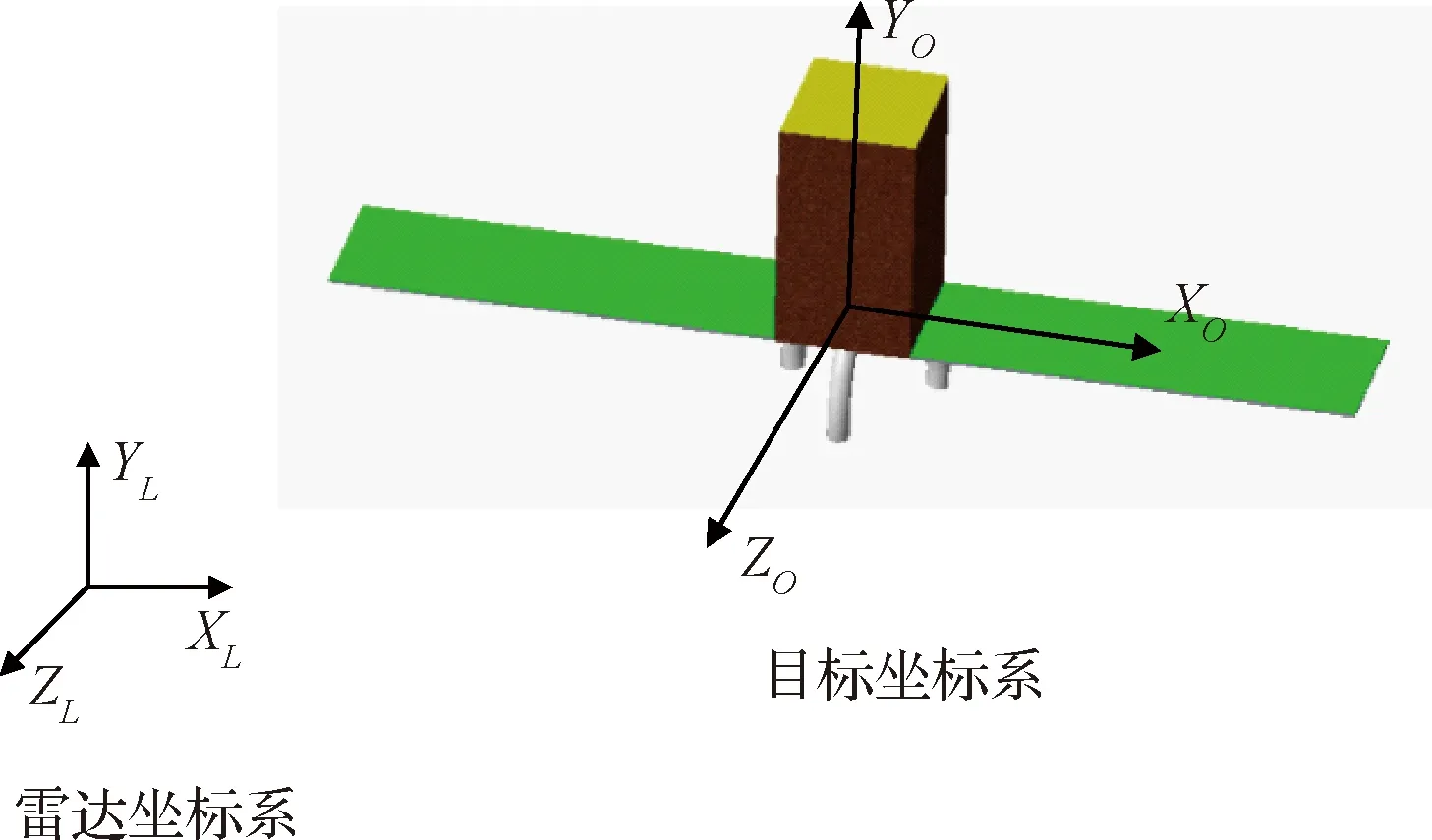
图6 扫描工况坐标系
2.2 点云配准实质
点云配准是通过匹配具有重叠部分的数据集,将不同视场下得到的三维数据变换到同一坐标系下,得到信息更加丰富完整的目标三维点云数据,计算出点云间的欧拉变换关系,即旋转变换矩阵R和平移向量T。
现采用线阵扫描型激光雷达进行N次扫描,得到N个视场点云数据,假设两组相邻点云数据Ni和Ni+1是对同一目标在不同成像视角得到的,配准目的便是通过平移和旋转变换将Ni+1变换到Ni坐标系下,定义为N′i+1:
N′i+1=R(α,β,γ)×Ni+1+T(tX,tY,tZ)
(11)
其中,R(α,β,γ)为旋转矩阵;T(tX,tY,tZ)为平移矢量;α,β,γ分别为绕X轴、Y轴、Z轴逆时针旋转的欧拉角;tX,tY,tZ为三个坐标轴正方向的平移量。旋转矩阵R(α,β,γ)可以表示为:
R(α,β,γ)=
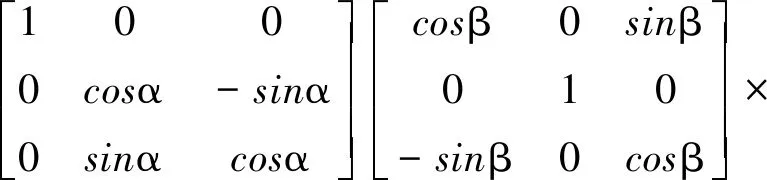
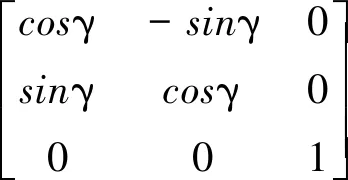
(12)
通过选取合适的变换角度和平移量,将Ni+1变换到Ni坐标系下,进行坐标系的统一处理,最后得到的N′i+1与Ni即为所需要的配准结果。
2.3 运动特性初值
1)统计配准参数与对应时间数组
通过上一步配准,获取目标相邻扫描时间内运动的旋转矩阵与平移向量,以初始时刻目标所在位置为位姿起始点,对应位姿增量叠加可以获得目标位姿-时间函数。通过配准获得参数如式(13)所示:
(13)
2)计算第i次旋转平移运动增量
旋转平移矩阵形式为(旋转次序依次为:Z-Y-X):
(14)
(15)
旋转运动增量:
(16)
平移运动增量:
(17)
式中:sX与cX代表绕X轴旋转的正弦与余弦值;Y轴、Z轴同理。
2.4 迭代配准
实现点云精配准现今主流的核心算法是ICP算法,该算法精度很大程度上取决于预先给定的位置姿态初值,即需要先进行点云粗配准,航天器一般具有较为明显的平面几何特征,现采用RANSAC算法提取目标点云特征点进行粗配准[15]。
1)点云粗配准
设由线阵雷达获取的点云数据集为P,从中随机选取三个点:P1(x1,y1,z1);P2(x2,y2,z2);P3(x3,y3,z3)。然后根据三点位置确定平面S:z=Ax+By+C,参数A,B,C由式(18)确定:
(18)
统计平面S上的点的个数,设定平面厚度为2σ,计算P中任何一点Pi到平面S的距离di,di由下式计算得到:
(19)
统计di<σ的点的个数,记为S的得分数。重复上述步骤K次,选择出得分最高的平面S*,其中K的计算公式为:
(20)
式(20)中m为点云中总的点数,n为点云中特征点点数,由于m和n值都很大,采用近似计算,由下式计算K值:
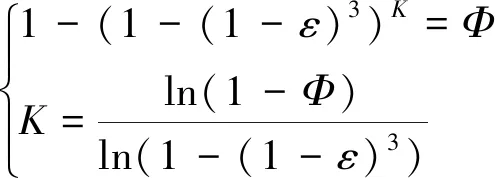
(21)
式中:ε为位于平面S*之外点所占比例的值(估计值),Ф为经过K次采样之后最后被选中的概率。
如图7所示,运用RANSAC算法提取相邻点云平面几何特征,图7(a)为相邻点云数据显示,图7(b)为两组点云相似特征点连线,据此进行点云粗配准。

图7 RANSAC算法
2)点云精配准
精细配准是一种更深层次的配准方法。经过前一步粗配准,得到了变换估计值。将此值作为初始值,在经过不断收敛与迭代的精细配准后,达到更加精准的效果。ICP算法(最邻近点迭代算法)最早由文献[16-17]提出,文献[16]采用的是待配准表面上点的配准方法,文献[17]采用曲面点集与切平面的配准方式。本文处理的点云数据形式为点集,而后者所采用的ICP算法对每个点的法向量进行计算,计算量较大,因此本文主要采用前者的待配准表面上点的配准方法。
算法基本原理:两点云P与Q,对于点云P中的每个点pi,搜索其在点云Q上的最近点作为与之相对应的点qi,然后依据对应关系求解使得式(22)中目标函数达到最小的刚体变换,即旋转矩阵R和平移向量T,并将该变换作用于源点云,迭代进行这一过程直到满足某一设定的收敛准则。
(22)
迭代终止条件:当目标相对于真值位姿精度不大于1°(3σ,三轴)时迭代终止。
3 三维重建
3.1 重建视场站位分布
假定失稳卫星最大自旋速度约为12(°)/s,定义旋转轴过模型质心,方向沿Z轴方向,并且目标在短时间内为匀速运动。现对Y轴方向采用最大自旋速度进行高压仿真,即三个方向速率分别为:vX=0(°)/s,vY=12(°)/s,vZ=0(°)/s。环绕目标沿Y轴按照每12度1帧提取点云可视化数据信息,如图8所示。
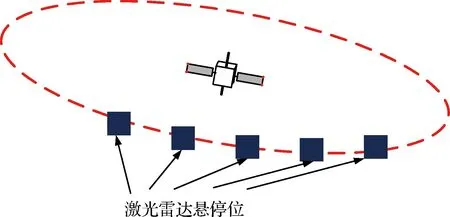
图8 多视场点云数据获取
3.2 畸变恢复
以雷达第一次扫描的初始时刻,目标所在空间位置建立目标坐标系,如果想把每一条畸变线信息恢复到目标形貌真实位置(x0,y0,z0),需要计算该条畸变点云线相对初始时刻所在坐标系的平移量和旋转分量,经过前面的步骤已经获取了目标天体的运动参数模型,可以通过对不同时刻采集的线信息进行逆运算以把多组线信息整合到同一时刻的空间位置,ti代表统计雷达在获取每一条线信息相对初始时刻所经过的扫描时间。则每一条雷达扫描线点云的逆向数据恢复模型为:
(23)
式中:
(24)
(25)
通过对多组相邻畸变点云数据的配准,可以获取沿时间延长的多组有限个相邻扫描时间内的相对位姿增量,如图9所示。
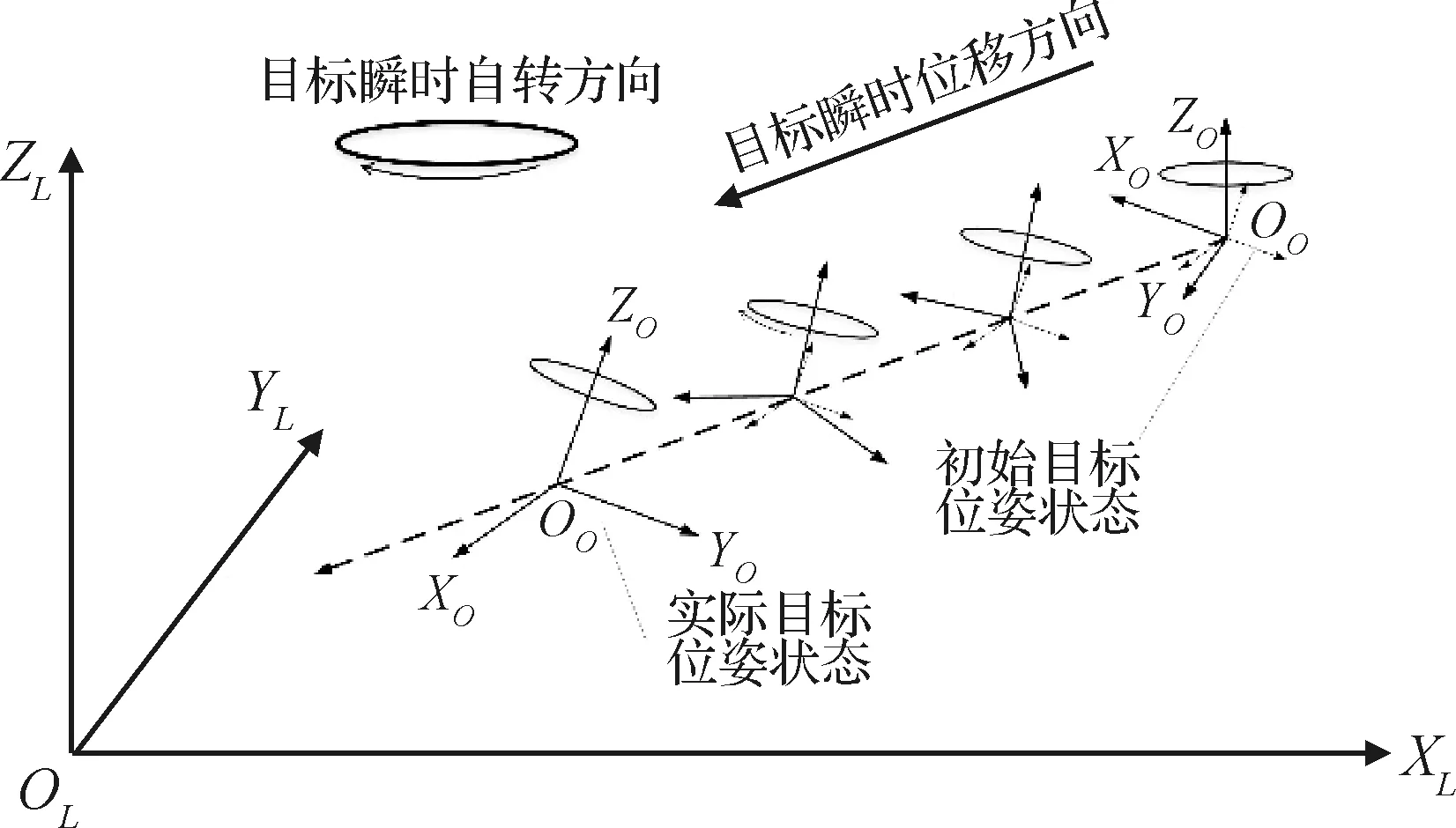
图9 目标瞬时运动状态
3.3 自修正式重建
本研究所采用的目标模型由卫星主体及太阳能帆板构成。在激光雷达环绕检测过程中,两侧的太阳能帆板会因主体及自身遮挡而导致点云关键部位特征突变,从而导致相邻点云配准时产生极大跃性偏差,对重建结果造成极大干扰。运用自修正原理,通过去除运动参数中存在的跳跃点,对环绕检测一周数据进行拟合,恢复跃性点处数据,并据此进行三维重建。
失稳目标在雷达相邻的两次扫描时间内能够保证有效重合扫描区域,基于此,对目标相邻扫描点云进行拼接;从而在目标旋转周期内,重复扫描、配准过程完成目标表面点云的三维重建。过程如下:1)获取第j次扫描点云,并作为重建起始,经上一步实现点云畸变信息恢复;2)获取第j+1次扫描点云,同样恢复畸变信息,与第i次点云进行配准,舍去重合区域;3)继续获取下一时刻扫描点云,重复上述过程;4)以当前时刻扫描点云与第j次点云配准重合度作为终止重建条件:当两处点云存在重合区域或者重合度大于设定阈值,认为目标完成一次周期自转,即完成重建工作。依据配准拟合结果,将各旋转角度对应结果还原到目标初始坐标系下,点云数据依次叠加,得到目标初始三维重建模型。
4 仿真校验
为了证明算法的有效性,进而验证本文提出的带畸变自修正式三维重建方法的可行性,现应用VS2013结合点云库(Point cloud library,PCL)对上述思想逐一进行仿真试验与校验。(文中算法结果均在CPU为Intel(R)Core(TM)i5-3210M CPU,2.50 GHz,内存为4 GB的PC机上运行所得,操作系统为Windows 7)
4.1 获取目标卫星三维点云模型
现对目标进行仿真重建,如图10所示,外形尺寸为16000 mm×6000 mm×3000 mm,本体尺寸为3500 mm×2000 mm×2500 mm。

图10 目标点云模型
4.2 配准
按照每12度1帧,逆时针环绕目标沿Y轴提取点云数据,可获得N个视场点云数据:
(26)
其中第1组0°为基准初始位置,其后每隔12°取样一次,最后一组为环绕检测360°后得到的可视化点云数据。32组目标环绕点云数据组如图11所示。

图11 32组目标环绕点云
按照上面提出的带畸变自修正式三维重建方法,针对获取的32组点云数据进行校验。
1)第i组与第i+1组相邻视角点云数据ICP配准。
2)获取该组旋转矩阵Ri与平移向量Ti。
3)将第i+1组点云根据旋转矩阵Ri与平移向量Ti,配准恢复到第i组点云状态下,相邻组点云配准如图12所示。

图12 相邻点云配准
4)将32组点云数据相邻两两进行配准,获取目标运动增量、解算目标瞬时运动参数。
5)然后对目标运动参数进行自修正式处理,去除特征突变干扰点。
6)依次恢复点云到初始几何位置,完成初始目标三维重建。
7)通过系统进一步迭代,位姿增量自收敛,直至最终满足重建精度要求。
4.3 配准结果分析
将32组点云数据,按照相邻组旋转配准,按照每12度1帧取样,每组旋转角度真值为12°,结果如表1所示。
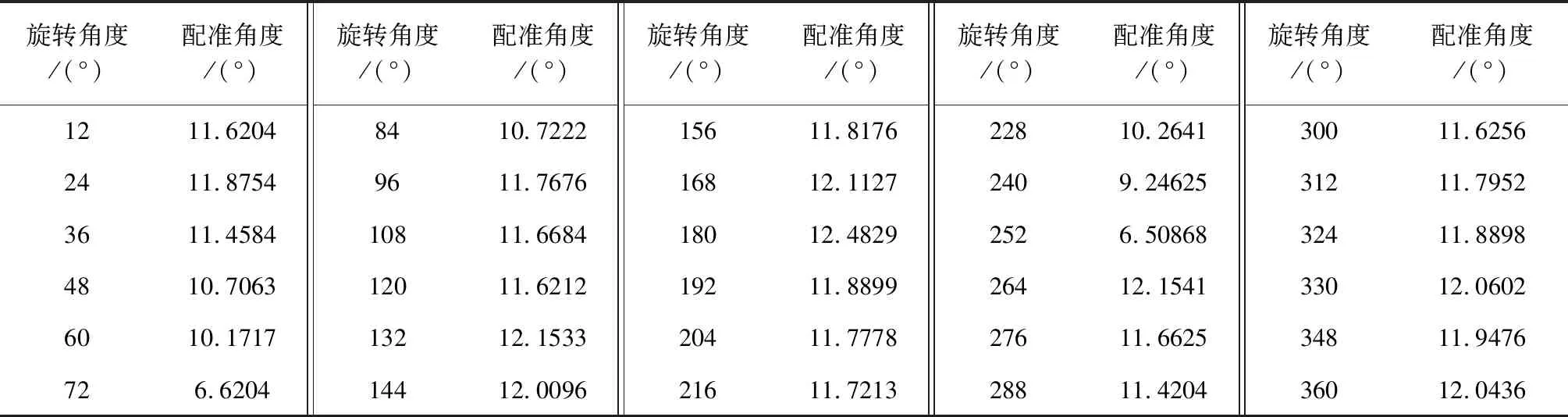
表1 相邻组旋转配准结果
如图13所示,实线为32组点云数据第一次配准结果,虚线为真值,点划线为拟合结果。其中当旋转角度为72°及252°时,模型单侧帆板在视角可视范围内消失,使得ICP配准时产生明显偏差。根据第2节阐述的方法,剔除两组较大偏差点,将剩余30组配准数据进行拟合,得到拟合结果。
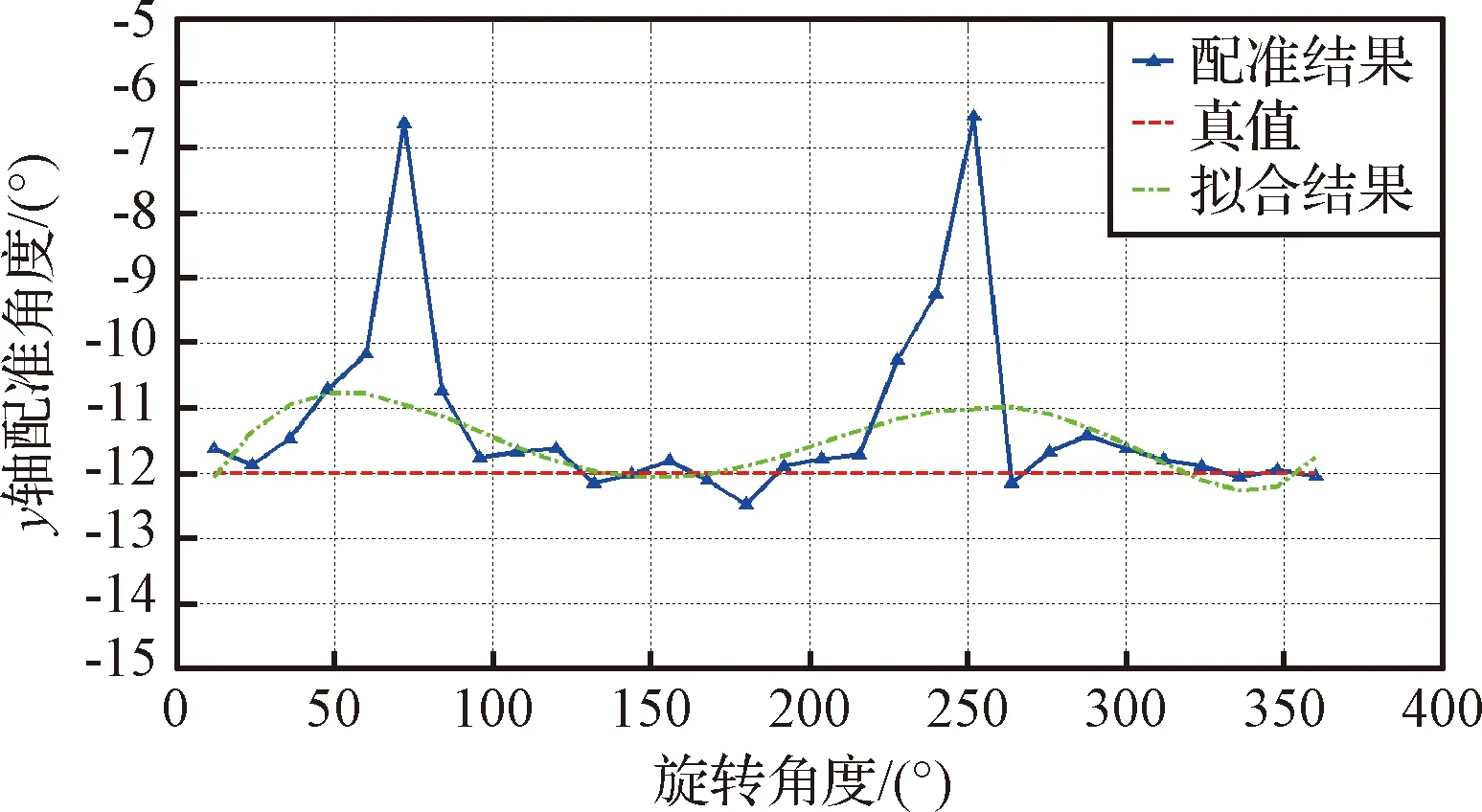
图13 相邻点云第1次配准
依据配准拟合结果,将各旋转角度对应结果还原到目标初始坐标系下,点云数据依次叠加,得到目标初始三维重建模型,第1次配准耗时为18337 ms。
4.4 迭代结束
本文获取的目标模型,在进行第6次迭代后,单次耗时为6779 ms,目标单位时间内运动增量均位于12°±1°内;在现有硬件配置环境下,配准总耗时为72467 ms,符合三维重建技术指标。第6次配准结果如表2所示,拟合结果及目标最终三维重建模型如图14~图15所示。
5 结 论
本研究以实现空间失稳目标三维重建为目的,解决目标失稳及线阵雷达扫描动态目标等多种因素所导致的目标三维模型无法精确恢复问题。首先根据角精度与测距精度两大判定条件计算畸变容忍度最大临界值,其次对目标点云进行自修正式迭代配准,直至满足三维重建要求。针对本文获取的目标模型,三维重建精度可达到±1°以内,重建总耗时在现有配置环境下为72467 ms。该方法不仅能够在理论上指导三维目标的点云数据配准、非合作目标的三维姿态测量和目标三维重建等工作,还能在实际应用中为线阵式测量技术的进一步发展提供新的研究方向。
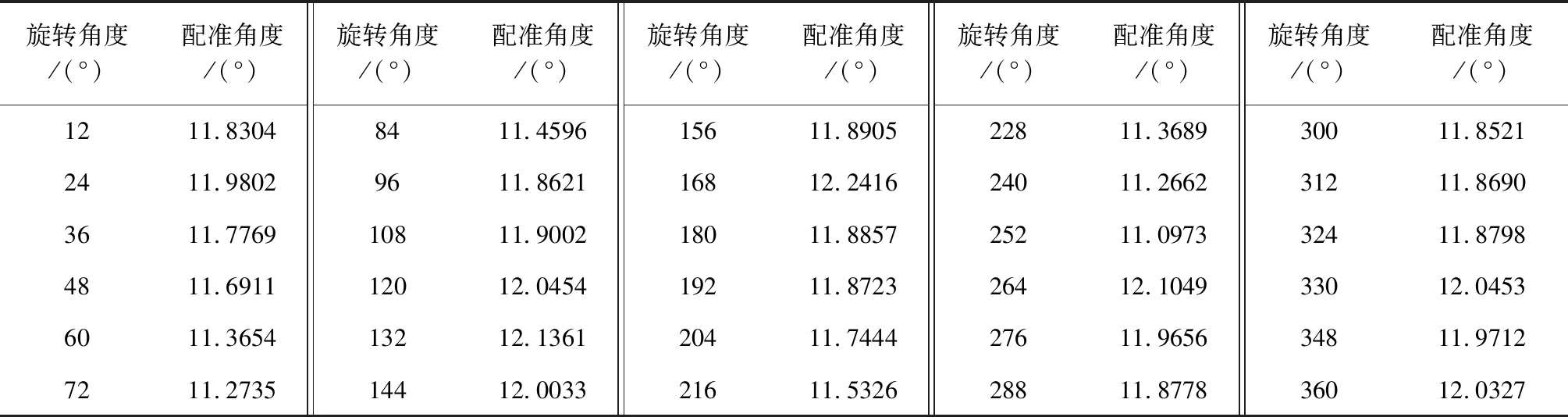
表2 相邻组旋转配准结果
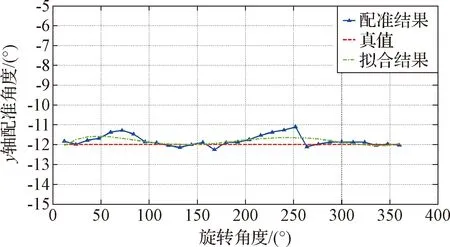
图14 相邻点云第6次配准

图15 目标最终三维重建模型

